Task Assignment for Heterogeneous Computing Problems using Improved Iterated Greedy Algorithm

Published Online June 2014 in MECS

The paradigm of Heterogeneous Computing has emerged as a hotbed for research in the recent times with the burgeoning demand for computationally invested applications requiring varied degrees of calculations and running on extremely divergent systems. With the advent of the phenomenon of cloud computing, these computations are often needed to transcend the geographical, cultural and linguistic boundaries. In other words, the heterogeneous system computation, entails apart from the dissimilar system configuration but also the geographical spread of these said systems.

Given such a scenario of geographic spread of processors, it is efficient and viable to divide a parallel application into cohesive tasks which can be executed independently on these individual processors. The caveat however lies in the fact that the efficiency of the said parallelization hinges on the concept of Task Assignment. Task Assignment deals with the assignment of tasks to processors with the single minded objective of minimizing the time and cost of computation.

Parallel computing is commonly used for executing computationally intensive applications like those used in database management, data-mining, networked videos and medical imaging. Instead of executing the application on a single processor, the application is divided into many tasks, and the tasks are executed in multiple processors concurrently. Since these processors differ in several key aspects including the cost of communication between two processors, heterogeneous computing finds practical application over its homogeneous counterpart. The concept of parallelization hinges on the key notion of task assignment. Task assignment problem involves assigning task modules to available processors in order to maximize processor utilization and minimizing

Turnaround time. Since, the execution time of a process is different on each processor; the total execution time in these systems is largely influenced by the order of assignment of tasks, done to different processors. The task assignment problem has been proves to be NP hard.

Tasks assignments are of two types – Static and Dynamic. Static task assignment involves finding a solution to the assignment problem before the start of execution of the large program on different processors. Hence, a longer time is needed to provide a better solution in the static method. This is in contrast to the

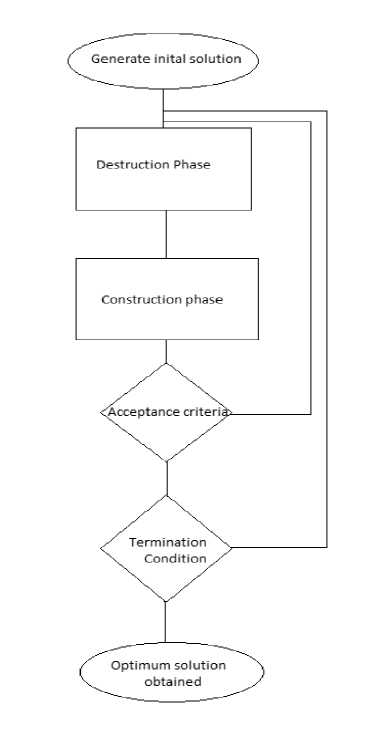
Fig 1: Flow chart depicting Iterated greedy method

Dynamic assignment wherein tasks of the large program are assigned to the processors while the program is actually being executed.

Task Assignment has traditionally revolved around the nucleus of performance and the methods have been built to satisfy these performance criteria. However the innate quality of these distributed systems is the vulnerability to machine and network failures stemming from the relative size and complexity of these machines when compared to the traditional centralized ones. This necessitates the evolution of a new strategy of task assignment algorithms which places equal emphasis on both performance and reliability. The importance of assuring reliability gains importance of gigantic proportions when the system in question deals with critical applications such as missile systems, aircraft control, and industrial process control where a collapse of the system even for a small duration could lead to exponentially high loss of money and life. The need for emphasis on reliability of task assignment algorithm is appreciated but is left for future research.

• A.    Task Assignment Methodologies

As the problem of task assignment is NP-hard for more than three processors [1], we aim to come as close as possible to the optimal solution using a polynomial time (heuristic) algorithm. Various algorithms have been put to use for making heuristics such as Greedy Heuristic genetic algorithm (GA) [2], simulated annealing [3], hybrid particle swarm optimization [4] and honeybee mating optimization [5].Most algorithms are based on graph matching and graph partitioning.

• B.    Iterated Greedy Heuristic Algorithms

Applying traditional approach using optimal solution methods to Task Assignment problem takes an acceptable amount of time for small problems but are generally inefficient for larger problems. This problem can be overcome by using a heuristic approach which takes lesser time but the benefit of optimal solution approach is lost. Thus there is a trade-off between time and optimality.

A greedy algorithm works on the principle of making a choice based on the optimal value at that point of time. In other words it chooses a locally optimal value at every juncture. Since the choice is locally optimal, there is a possibility of the final solution not being optimal, i.e. the global optimum might not be derivable from these locally optimal values. Thus a good greedy heuristic algorithm uses these locally optimal values which approximate to the global optimum solution. This is employed when the time of computing the values are of the greatest importance.

Greedy Algorithm produces a good solution, although it might not be optimal, it is often close to an optimal one in a reasonable duration of time. The algorithm has a downside, in that it is deterministic. This leads to the algorithm being stuck in a local minima rather than a global minima which is often guaranteed in a Dynamic Programming approach.

It makes use of a task graph and a processor-graph. While the task-graph denotes the dependency amongst the task modules, the processor graph defines the topology of interconnection amongst the processors. The iterated greedy algorithm starts with a heuristically constructed initial solution and then opting to improve the solution, with every iteration. The iterated greedy (IG) heuristic is one of the most efficient techniques used for solving task assignment problem as shown by [6].

• C.    Motivation for the work done

The paper is organized as follows. The problem formulation is discussed in Section 2 and the improved IG heuristic algorithm is given in Section 3. The result of application of proposed algorithm and the comparison with original algorithm is provided in Section 4. Concluding remarks are made in Section 5.

• II.    Problem Formulation

The task problem can be represented by a graph Task Interaction Graph (TIG): G (V, E). The TIG involves the various tasks (say, N tasks) that are used as vertices (V) of the graph (G) and (E) represents the communication required between those two tasks. The tasks are assigned to the various processors (P). Since we have assumed a heterogeneous system the execution times of the various tasks differs with change in the processor. The various execution times are taken in a matrix {ecij} where ecij represents the time taken for task i to execute on processor j. A weight wij corresponds with an edge (E) that represents the amount of data to be transferred between tasks i and j. As in a heterogeneous system the communication cost between processors could also differ, and this is represented by dkl where k and l are two processors. This value depends on distance between processors and it is the cost for transferring unit data between the two processors. This distance metric is considered to be symmetric, i.e. dkl= dlk. Additionally, we also assume that two tasks assigned to the same processor yields no communication overhead.

The task assignment problem involves trying to minimize the total time. The communication cost is calculated by multiplying the distance between the two processors with data to be transferred between the two tasks wij * dkl(when task i and task j are assigned to processor k and processor l respectively).

Let ϕ be a mapping which assigns tasks to processors, e.g. ϕ [i] =k implies that ith task was assigned to processor k. Let ϕ be the set of all possible mappings ϕ.

In our model, we consider two costs that are incurred – processor execution cost and   inter-processor communication cost.

The processor execution cost (PEC) is given by,

N

PEC = ^ ec^

i=1                      (1)

The inter-processor communication cost (IPCC) is given by,

N-l N

IPCC — ^ ^ ^(Op(j")^cu i=l j=i+l                    (2)

The objective is therefore to Minimize Cost=PEC+IPCC subject to the constraints:

• •    Resource Constraints:

  
  
  

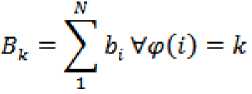
• •    Processor is used if a task is allocated at least one

• •    And all the tasks should be allocated only once.

• III.    Improved iterated greedy algorithm

The algorithm starts with the generation of an initial greedy solution. This initial solution is generated randomly and is followed by a series of iterations that are performed to get optimized solutions. Akin to the algorithm proposed in [1], the algorithm has four basic steps – Construction, Destruction, Optimize and Acceptance.

In the destruction phase, some d tasks are removed from the incumbent solution and in the construction phase, these d tasks are reassigned to the available processors. The decision i.e., to accept this new arrangement or not, is taken by the acceptance criteria. This whole process is iterated until a stopping condition is met.

An outline of iterated greedy algorithm as given in [1],

Procedur e IteratedGreedy {

Xo= GenerateInitialSolution;

X = LocalSearch (Xo);

Repeat

Xp = Destruction(X);

XC = Construction (Xp);

X = LocalSearch (Xc);

X = AcceptanceCriterion (X, X*);

Until termination condition met

}

• A.    Initial Solution

Initial solution is randomly generated, by assigning some random task to each processor such that no constraints on resources and memory are violated. The number of iterations required to generate the optimal solution depends on the initial solution. The proximity of the initial solution to the final solution governs the number of iterations needed to solve the task assignment problem. The closer the initial solution is to the final solution, the lower is the number of iterations required (on an average). Thus, the random solution technique employed to identify the initial solution forms the basis for implementing parallel processing in the iterated greedy methodology.

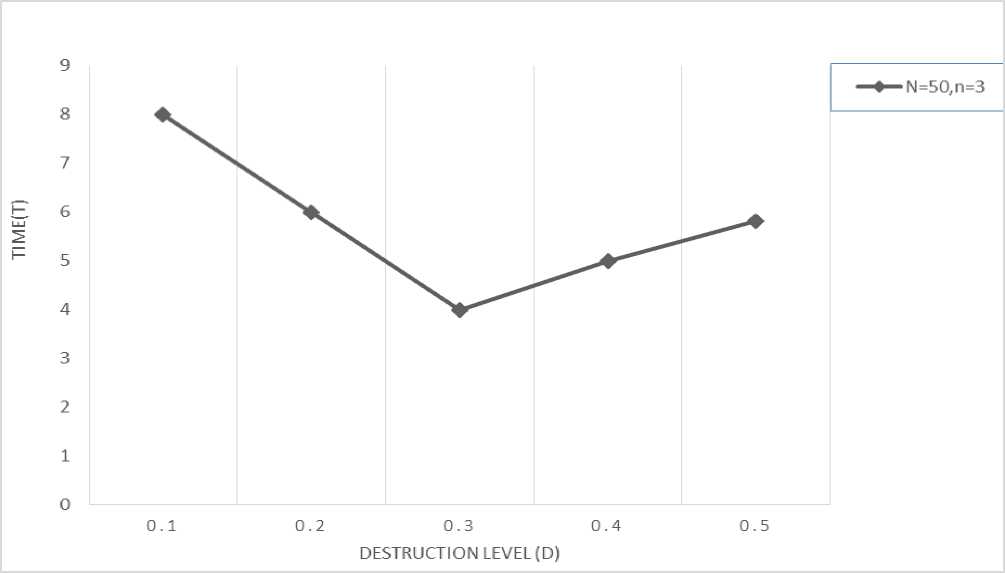
Fig 2: A plot of total time consumption (T) against the destruction level (D) for value N=50, n=3

• B.    Destruction Phase

In this phase, a certain number tasks are chosen and they are removed from the incumbent solution. As stated in [6], the number of tasks to be removed (d) is chosen randomly from 0 to N. The complexity of this phase is O (d*N). It can be seen that the number d influences the total running time of the algorithm.

From Fig. 1, the plot reveals that the total time consumption (T) takes a local minima at D=0.3. Further extension will show that the local minima is also a global minima. Thus in order to ensure a minimum value for the time consumption, we maintain d as 0.3N since it yields better performance as seen from [6].

• C.    Construction Phase

After removing d tasks from the destruction phase, we have a partial assignment solution ϕ p. The removed tasks are re-assigned to the available processors such that we have minimum cost according to greedy constructive heuristic technique adopted from [7], while also taking care that no constraint is violated. This is done for each removed task. The complexity of this phase is O (d*N*K).

• D.    Acceptance Criteria

The acceptance criterion specifies the acceptability of the new assignment solution. Usually, a new solution is accepted if it is better than the incumbent solution. However, as mentioned in [6], it is sometimes better to accept slightly worse solution in order to avoid stagnation that may occur due to insufficient diversification.

In [6], the approach was to use an exponential probability function to determine whether to accept a worse solutionor not. In this paper, however, we do away with the probability function. Instead, we consider a solution with System Cost < 1.2*current cost as a candidate solution. The value for this was arrived at after the observation that it performs better heuristically.

• E.    Termination Condition

We could have various terminating conditions like total number of iterations, computation time-limit cutoff etc. Since our algorithm will be compared with the other heuristic algorithm mentioned in [6], we will have computation time-limit as our stopping criteria.

Initiating parallel processing in the problem.

The parallel processing is implemented in the generation of initial solution by calling some ‘m’ processes to generate their own initial solution and perform the three phase’s namely-destruction, construction and acceptance for some number of iterations. After a certain number of iterations, during which these processes communicate with each other to find the solution which is minimum, a continue signal‘s’ is sent to these processes and it continues with further iterations to arrive at the final solution and all other processes, which have not received the “continue” signal, are stopped after completion of the iterations. The process returns the final solution back to the main process.

• F.    Pseudo code for proposed algorithm

paralliteratedgreedy()

{ min_sol,sol_id;

if(root process)

{ for(i=1 to no_of_processors)

receive(par_sol,procs_id)

//root processor//

//communication phase//

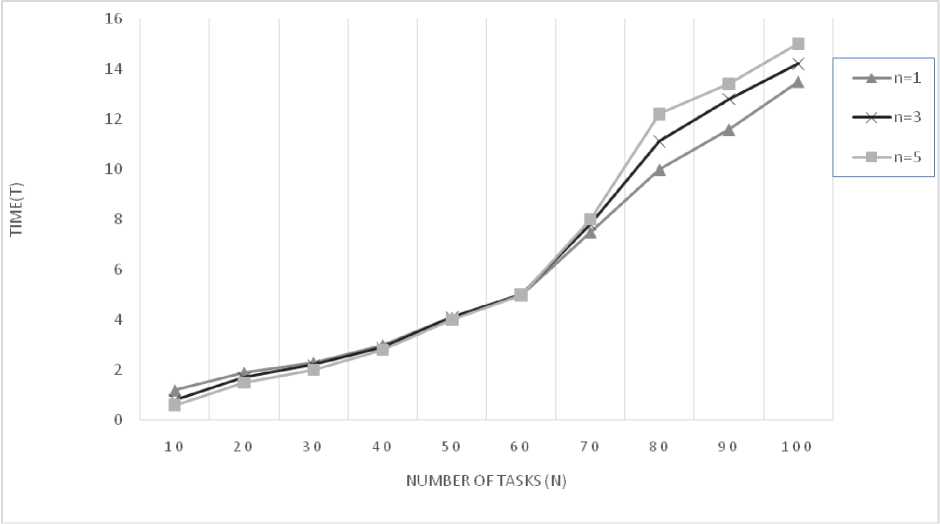
ifpar_sol

{ min_sol=par sol sol_id=procs_id

} send(continue,sol_id);

signal // else

//send back continue

//operations of other

processes//

{

Xo= GenerateInitialSolution;

X = LocalSearch(Xo);

Repeat

Xp = Destruction(X);

Xc = Construction(Xp);

X = AcceptanceCriterion (X, X*);

Until m iterations

} send(X,rootprocs_id);    // Sending locally minimum value to root processes for acceptance // receive(signal,rootprocs_id);

if(signal=contnue)

{

Repeat

Xp = Destruction(X);

Xc = Construction(Xp);

X = Optimize(Xc);

X = AcceptanceCriterion (X, X*);

Until termination condition met

} send (x,rootprocs_id);    // sending optimal solution back to main process //

}

}

• IV.   Experimental results

The proposed algorithm was implemented on a Dev C in a Intel core i3 processor. The algorithm is based on the iterated greedy algorithm proposed in [6], incorporating the concept of parallel processing using Message Pass Interface (MPI) without the local search.

Values obtained from the execution of the said algorithm resulted in the plot shown in Fig. 1. The total time consumption plot was made against the number of tasks (N) for different values of the number of parallel processors (n). Without much loss of generality, it can be stated that the value for n=1 is approximately equal to the corresponding value of duration of convergence obtained in [6].

• V.   Conclusions & Recommendations

It is inferred from the graph in Fig. 1 that the iterated greedy algorithm with the concept of parallel processing is very efficient and converges faster for smaller value of N (the number of tasks). This is, as a result of the reduced number of iterations needed. With the increase in tasks, however, the overhead for communication overweighs the advantage of parallel processing and increases time taken for convergence.

For smaller value of N, It is also observed that with the increase in the number of parallel processors (n), the duration of convergence is significantly lesser.

• VI.   Further Work

The following improvements will be the focal point of our further research:

• •    Utilizing a more robust approach to arrive at the initial solution, than the hitherto random methodology, will yield an initial solution much closer to the final optimal solution, thus reducing the number of iterations

• •    Adopting the concept of parallel processing in the destruction phase, the need for random initial solution is overcome by using random destruction of tasks.

• •    Incorporating the element of reliability into the algorithm to enhance the application of it in critical systems.

  

  Figure 3: A plot of the total time of computation (T) against the number of tasks (N) for different number of processors (n)