Течение вязкого газа в вертикальной трубе

Среди известных точных решений [1-12] уравнений движения вязкого газа, до сих пор отсутствует точное решение для течения в трубе. Решению для течения в трубе, в котором используются наиболее точные (и наиболее сложные) формулы для зависимости коэффициентов вязкости и теплопроводности от температуры (они будут приведены ниже при постановке задачи), посвящена, данная статья. Чтобы обеспечить стационарное движение вязких жидкости или газа, в каналах и трубах, необходимо компенсировать потери, связанные с трением. Нужна, некоторая «проталкивающая сила». Так, например, в классическом

течении Пуазейля (течение вязкой несжимаемой жидкости в прямой трубе круглого поперечного сечения) [13] такая сила создается в резулвтате продолвного перепада давления. В точном решении Пуазейля скорость направлена вдоль оси трубы и ее величина зависит только от расстояния до этой оси (от радиуса). В данной статье предпринята попытка получить точное решение для течения вязкого газа, в котором скорость также направлена вдоль оси трубы и ее величина зависит только от радиуса (течение Пуазейлевского типа). Сложность этой задачи состоит в следующем. Для такой скорости из уравнения неразрывности следует, что плотность также зависит только от радиуса. Поэтому на каждой линии тока (т.е. вдоль продольной координаты), в силу уравнения состояния, температура должна меняться вместе с давлением, и поэтому при наличии продольного градиента давления температура также будет меняться вдоль продольной координаты. Вместе с температурой будут меняться коэффициенты вязкости и теплопроводности. В итоге уравнения движения вязкого газа [13, гл. XV] при наличии продольного градиента давления не упрощаются до обыкновенных дифференциальных уравнений (ОДУ), как это имеет место в вязкой несжимаемой жидкости в решении Пуазейля, и остаются уравнениями в частных производных, точное решение которых авторам данной статьи найти не удалось. Чтобы получить точное решение Пуазейлевского типа была использована идея статьи [12], где для плоскопараллельного течения между стенками было рассмотрено течение, в котором давление постоянно, а роль проталкивающей силы играет сила тяжести. Для этого в [12] стенки были расположены вертикально. В результате в [12] уравнения движения вязкого газа упростились и свелись к решению системы двух ОДУ второго порядка (все гидродинамические параметры зависели только от горизонтальной координаты). Для соответствующей этим уравнениям задачи Коши выполнялись условия теоремы существования и единственности решения. Поэтому, хотя точное решение упомянутого ОДУ в [12] получить не удалось, и для расчета параметров течения использовалось численное интегрирование, решение [12] считается точным решением уравнений движения. Аналогичная ситуация имеет место в задаче Блазиуса [14]. Решение задачи Блазиуса считается точным, хотя сводится к задаче Коши для ОДУ третьего порядка, общее решение которого неизвестно и в общем случае рассчитывается численным интегрированием. В данной статье также рассмотрено течение, в котором роль проталкивающей силы играет сила тяжести, и труба расположена вертикально. Давление в трубе считалось постоянным. Поэтому следует уточнить, что для реализации рассматриваемых течений в земных условиях, при которых давление растет с высотой, необходимо либо искусственно создавать разрежение снизу (отсос воздуха насосом), либо нагнетать воздух сверху.

2.    Основные обозначения, постановка задачи, система ОДУ

Рассмотрим стационарное течение совершенного (закон Менделеева-Клапейрона) вязкого газа в вертикальной цилиндрической трубе круглого поперечного сечения (ось трубы параллельна вектору ускорения свободного падения g). Попытаемся найти точное решение, в котором давление газа постоянно, скорость, плотность и температура изменяются только вдоль радиального направления, при этом не равная нулю скорость имеет только вертикальную компоненту (в направлении g).

Введем цилиндрическую систему координат Orpz, в которой ось Oz совпадает с осью трубы и ее положительное направление совпадает с направлением вектора g. Обозначим: r — радиальная координата, отсчитываемая от оси трубы, К — скорость течения вдоль оси z. Т — температура газа, р — плотность газа, р — давление.

Будем считать, что для коэффициента вязкости ц справедлива формула Сазерленда РТА- * ( Т_V/2 Т * +TS ц( ) ц ^т*)    Т + Ts ’ где для воздуха ц* — 1.715 • 10-5 кг/(м • с) Т* — 273 К, Ts — 111 К. Эта формула дает погрешность менее 2% для диапазона температур 170-1900 К и давления менее 10 атм, а при температуре Т > 1500 К отсутствует диссоциация [11].

Перейдем к формуле для коэффициента теплопроводности А. В диапазоне температур 170-1900 К при том же давлении аналогичную точность дает формула, предложенная в монографии [15] и имеющая вид, подобный формуле Сазерленда, а именно:

А(Т) = А* ( ТД+Д,                      (2)

_т * _т + р^

где для воздуха А* = 2.412 • 10^-2 Вт/(м • К), Т * = 273 К, Т а = 194 К. Формулу (2) будем использовать для вычисления коэффициента теплопроводности.

Движение вязкого газа описывается уравнением неразрывности, динамическими уравнениями Навье-Стокса, уравнением баланса тепла и уравнением состояния [13, гл. XV]. Если движущийся вязкий газ имеет постоянное давление р = рд и скорость, имеющую одну только ненулевую z-компоненту V в прямоугольной декартовой системе координат Оху z и сонаправленную вместе с положительным направлением оси z с вектором g, а все газодинамические параметры зависят только от поперечных координат ж и у, то динамическое уравнение Навье-Стокса по координате z и уравнение баланса упрощаются и принимают вид

№. + (pV₄ )_у + рд = 0, (АТ.). + (АТ_У )_у + . V² + V') = 0, где д = |g|. Два других динамических уравнения Навье-Стокса и уравнение неразрывности в рассматриваемом случае выполняются тождественно. Переходя от декартовых координат ж, у, z к цилиндрическим г, р, z и учитывая симметрию круглого сечения (V, = Т, = ц, А, = 0), имеем

(гцV‘)‘ + рдг = 0, (гАТ‘)‘ + гц(V')² = 0, р = рКТ = р_д >  0.            (3)

Здесь штрихом обозначена производная по г, R — универсальная газовая постоянная, отнесенная к молярной массе воздуха.

Приведем уравнения к безразмерному виду. В качестве характерных значений скорости, температуры, плотности, коэффициентов вязкости и теплопроводности выберем их зпачепия при Г = 0 II обозначим Vg, Тд, рд, Цд II Ад соответствешю. где Цд II Ад вычислены по формулам (1) и (2) для Т = Тд, а безразмерное расстояние до оси трубы определим как Г = г/гд. г,то гд = л/ЦgVg/рgд (в частности. при р = 1 атм. Тд = 293 К. д = 9.81 м/( ² и скорости V o = 1 м/с значение гд равно 0.0012 м). Заметим, что гд в общем случае нельзя считать характерным поперечным размером, поскольку эта величина может отличаться от радиуса трубы.

Первые два уравнения системы (3) в безразмерных переменных V = V/Vg, Т = Т/Тд, р = р/рд. V = ц/цд. А = А/Ад 11 Г = г/гд ИМСЮТ ВИЧ

(Г/zV Д + 7=0 (ГАТ')' + ar/z(V ‘)2 = 0,(4)

где a = цдЕд2/АдТд. В (4) штрихом обозначена производная по Г. В безразмерных переменных формулы (1) и (2) переходят соответственно в

Г Г

ц(Т)=Т3/2/J"' и \(Т)=Т3<21 'J.(5)

1 + 1s                 7 + ТА

Дополним (4) начальными условиями. Как функции радиуса, безразмерные скорость V и температура Т по построению и ввиду симметрии задачи таковы, что

V |_ =Т|_ =1 и VТ =ТТ =0.(6)

г=0 г=0              г=0 г=0

Таким образом, поставлена задача Коши для двух ОДУ второго порядка (4-6). В зависимости от значений параметра a она определят различные решения. Скорость газа в этих решениях зависит от безразмерной переменной Г = г/гд. Как будет видно из дальнейших вычислений, для каждого решения существует такое значение г_ш, при котором скорость V обращается в нуль. Поскольку на стенках (неподвижной) трубы в силу условия прилипания скорость газа должна быть равна нулю, получаемые решения задачи (4-6) будут описывать течение в трубе радиуса г_№ = Г_№гд. При этом нужно исключать те решения, в которых внутри трубы (размерная) температура Т хотя бы в одной точке выходит из диапазона 170-1000 К.

Таким образом, найдено решение системы уравнений вязкого газа через решение системы ОДУ. По аналогии с решением Блазиуса и решением [12] полученное здесв решение можно считать точным решением.

3.    Результаты расчетов

Для численного решения поставленной задачи система (4) из двух ОДУ второго порядка была сведена к системе из четырех ОДУ первого порядка:

V ‘ = Р Р’ = -   - (1 + I) Р Т’ = f, f‘ = -аЦ Р² - <1 + y)f, (7)

цТ \r р;                    А     у г А / с начальными условиями (6) следующего вида:

V |    = Т|_ =1 и Р‘|-_п = f’l- =0.                        (8)

г =0       г =0               г =0       г =0

Здесь ц(Т) и А(Т) — коэффициенты вязкости и теплопроводности, определяемые соответственно первой и второй формулами (5). Использовалась схема Рунге-Кутты четвертого порядка точности. Расчеты производились в диапазоне осевых скоростей V от 10-3 м/с до 1020 м/с, при р = 101325 Па, То = 293 К, д = 9.81 м/с2. В каждом из случаев был посчитан (размерный) радиус трубы г™ (табл. 1).

Таблица!

Зависимость радиуса трубы г™ от осевой скорости V 0

V0, м/с	г№, м	V0, м/с	г™, м	V0, м/с	г™, м
0.001	8.0 • 10-3	10	7.8 • 10-1	200	4.2
0.01	2.5 • 10-2	50	1.4	340	4.9
0.1	7.8 • 10-2	100	2.5	680	5.4
1	2.5 • 10-1	150	3.5	1020	6.9

Для трех различных значений осевой скорости V0 профили безразмерных скорости V п температуры Т изображены на. рисунках 1 и 2. Для других значений V0 прос]шли V и Т имеют похожий вид и расположены между профилями для осевых скоростей V0 = 10^-3м/с и V0 = 1020 м/с. При этом, как для V, так и для Т, профиль, соответствующий большей осевой скорости V0, проходит ниже профиля, соответствующего меньшей осевой скорости.

Вычисления показывают, что в случае низких осевых скоростей (V 6 200 м/с) профиль температуры с точностью до 2% (относительно Т = 1) может быть рассчитан по интерполяционной формуле Т (г) ~ 1 — ат⁴/64.

Вычисления также показывают, что в случае V0 6 200 м/с температура Т меняется менее чем на 2% в диапазоне г : 0 6 I 6 f_w. Следовательно, слабо изменяются и коэффициенты вязкости Ц и теплопроводности А, а значит, и сам газ почти не меняет своих свойств вдоль сечения трубы. Поэтому приближённый профиль скорости можно получить, полагая, что температура Т постоянна и равна 1. В этом случае первое уравнение в (4)

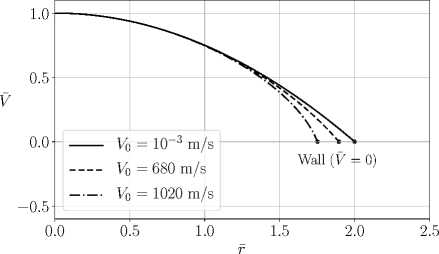
Рис. 1. Профили скорости. Точки, соответствующие стейке трубы, подписаны словом «Wall»

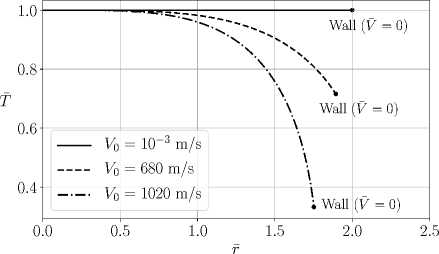
Рис. 2. Профили температуры. Точки, соответствующие стейке трубы, подписаны словом «Wall»

принимает вид (rV ‘)‘ = —г. Решением такого уравнения, с учётом начальных условий (6), будет параболический профиль скорости

V(r) та 1 - г2/4. (9)

Расчеты показывают, что для диапазона осевых скоростей до 200 м/с решение (9) отличается от точного решения не более чем на 1% (относительно осевой скорости V = 1). Поэтому значение для радиуса трубы r_w та 2, полученное из (9), дает с точностью до 1% радиус трубы в размерной форме r_w та 2 poVo/pog.

4.    Верификация программ расчета течений вязкого газа

Для верификации удобно использовать точные решения, представленные через элементарные и другие известные функции (например, функции Бесселя). Найденное выше точное решение не является таковым, поскольку требует численного решения системы ОДУ. Однако, как показано выше, для осевых скоростей Vo от 10^-3 м/с до 200 м/с при р = 101325 Па. То = 293 К. g = 9.81 м/<² и для радііуса трубы r_w = 2y/poVTPog профиль скорости точного решения точностью до 1% (относительно Vo) представляется формулой

V(г) та Vo (1 - r2/(2rw)2) , ' (10) а температура точного решения с точностью до 2% (относительно To) представляется формулой

Т (г) та To (1 — ) . С¹¹) 64AoTo rW /

Значения параметров с нижним индексом 0 определены во втором разделе в тексте между формулами (3) и (4). В таком виде (в виде элементарных функций радиуса) приближенные точные решения удобно использовать для верификации численных методов расчета течений вязкого газа. При уменьшении осевой скорости Vo ошибка приближенных формул (10) и (11) уменьшается. Так, например, для осевых скоростей 150 м/с и 100 м/с ошибка формулы (10) не превышает 0.5% и 0.2% соответственно, а ошибка формулы (11) — 1% и 0.3% соответственно.

5.    Заключение