Технические характеристики инвариантной системы обработки информации при некогерентном приеме и неточном определении порогов

Основным требованиям к системам обработки информации является ее безыскаженная передача по каналам связи с переменными параметрами.

Существуют методы, которые сводятся к использованию АРУ, разнесенного приема, адаптивных методов с обучающим сигналом, систем с обратной связью.

Эти методы имеют как положительные, так и отрицательные стороны. Одним из отрицательных моментов указанных выше методов является трудность реализации алгоритмов передачи сигналов с многоуровневой амплитудной модуляцией.

В предлагаемой работе синтезирован алгоритм передачи многоуровневых амплитудно-модулированных сигналов по каналам с переменными параметрами и произведена количественная оценка помехоустойчивости при некогерентном приеме.

Постановка задачи. Имеется канал связи, ограниченный частотами f _н и f _в. Состояние канала связи определяется интервалом стационарности, внутри которого действие мультипликативной помехи описывается постоянством коэффициента передачи k ( t ) на определенной частоте.

Алгоритм приема определяется несущей частотой, задаваемой как средняя частота канала, амплитуда которой промодулирована прямоугольными импульсами.

Требуется определить технические характеристики инвариантной системы передачи при неточном определении порогов.

Решение поставленной задачи. Каждый передаваемый блок будет содержать информационную часть и последовательность обучающих сигналов S _об.

На приемной стороне обучающие сигналы усредняются и используются для демодуляции информационной части блока.

При этом из-за изменения параметров канала связи информационные и обучающие сигналы зашумлены аддитивной помехой.

Для уменьшения влияния аддитивных шумов канала связи используется операция усреднения обучающих сигналов в каждом блоке [1].

Проведем анализ помехоустойчивости инвариантной системы (рис. 1), где использованы два канала обработки.

В первом канале, состоящем из синхронного детектора (СД) и первого решающего устройства (РУ1), производится оценка коэффициента передачи канала и дисперсии нормального шума, которые в дальнейшем используются для расчета порогов при демодуляции инвариантов.

Во втором канале использована некогерентная система с линейным детектором (ЛД) и вторым решающим устройством (РУ2). В этом канале собственно и демоду-лируются сигналы приема.

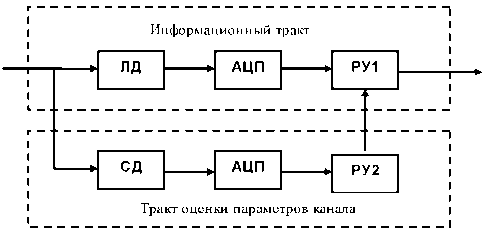
Рис. 1. Укрупненная структурная схема инвариантной системы: ЛД - линейный детектор; АЦП - аналого-цифровой преобразователь; РУ1 - решающее устройство первое;

СД - синхронный детектор; РУ2 - решающее устройство второе

Оценим количественные показатели предлагаемого метода.

Работа информационного тракта. Принцип работы информационного тракта состоит в выделении огибающей сигналов приема совместно с нормальным шумом с помощью ЛД. Результат преобразования в АПЦ в дальнейшем записывается в РУ1.

В РУ 1 производится вынесение решения в пользу того или иного инварианта.

Как известно [2], при использовании ЛД появляется смещение математического ожидания. Математическое ожидание вычисляется по следующей формуле [2]:

m р =о

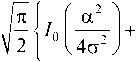
а ² 2 g ²

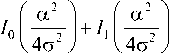
4 g ²

где т р - величина математического ожидания; g ² - дисперсия компонент нормального шума; I 0 и 1 1 - модифицированные функции Бесселя нулевого и первого порядков; а = k - INV l , где к - коэффициент передачи канала; INV l - 1- й передаваемый инвариант.

Величина дисперсии на выходе ЛД вычисляется по следующей формуле [2]:

G p = т ₂ - т р = 2 g ² +а ² - т р .          (2)

Для принятия решения в пользу того или иного инварианта необходимо знать значения порогов для каждой пары инвариантов.

В свою очередь, для оценки порогов необходимо вычислять т р и g р ² .

Это можно сделать с помощью тракта оценивания параметров канала (рис. 1), где производится расчет величин к и g ².

Совместная работа информационного тракта и тракта оценки параметров канала состоит в приеме и записи в РУ1 и РУ2 значений амплитудно-модулированных информационных и обучающих сигналов некогерентным приемником и вычислению на их основе оценки инварианта.

На основе последней и вычисленных порогов принимается решение в пользу того или иного инварианта.

Произведем расчет вероятности ошибочного приема при многоуровневой инвариантной амплитудно-модули-рованной передаче сигналов. Для этого воспользуемся известным подходом [3]:

zp                        го

Р пер = P j W 2 ⁽ z ) dz + P 2 J W 1 ⁽ z ) dz ,        (3)

0                   zp где Рпер - вероятность перехода первого инварианта во второй и наоборот; Р1 - вероятность появления первого инварианта; P2 - вероятность появления второго инварианта; первый интеграл - это вероятность появления второго инварианта, когда послан первый; второй интеграл -это вероятность появления первого инварианта, когда послан второй инвариант; zp - пороговое значение, необходимое для вычисления Рпер при известных Р 1 и Р2.

Величина z_p определяется с помощью наилучшей байесовской оценки путем минимизации Р _пе р по z_p . При неизвестных Р 1 и Р ₂ выбираем Р 1 = Р ₂ = 0,5.

Как видно из выражения (3), необходимо знать аналитическое выражение W 1 ( z ) и W ₂( z ).

Для когерентного приема расчет величин W 1 ( z ) и W ₂( z ) известен и приведен в [1]. Такой же подход можно использовать и при некогерентном приеме.

Итак, величина оценки инварианта в такой системе рассчитывается как

N

К к • INV , +^( i ) )

IN^V l = .-- ⁵ об ,

7 ЕЕ ( k • ⁵ об ⁺п^{( т} , j ) )

L т = 1 j = 1

где INV l - l -й передаваемый инвариант; £ ( i ) - i -е значение релеевской помехи; к - коэффициент передачи канала связи; 5 об - значение обучающего сигнала; п ( т , j ) - j -е значение релеевской помехи в т -й реализации сигнала 5 об ; N - число отсчетов, взятых по огибающей INV l или 5 об ; L - число обучающих сигналов.

Без ограничения общности примем 5 об = 1, так как 5 об > 0, и можно разделить значения инвариантов INV l и среднеквадратического отклонения на 5 об .

При 5 об = 1 получаем следующее аналитическое выражение:

N

£ ( к • INV i -Л i ) )

INV;=-т^•        ⁽⁴⁾

7 Е£( k ⁺п^{( т} , ^j ) )

^L т = 1 j = 1

Для расчета Р _пер необходимо знать математические ожидания и дисперсии числителя и знаменателя выражения (4).

Для их расчета воспользуемся следующим подходом. Математическое ожидание числителя (4) будет равно ^т числ = ^т р • N .                    (5)

Дисперсия числителя (4) будет равна

D числ = N -G p ,                    (6)

где тр и gр2 вычисляются в соответствии с выражениями (1) и (2). Математическое ожидание знаменателя (4) после преобразований будет равно m знам = m р2 " N ,                 (7)

где m_{p 2} вычисляется в соответствии с (1) при a = к, так как вместо INV _l используется S _об = 1.

Дисперсия знаменателя (4) будет равна

D знам = N F 2 lL ,              (8)

где а ² _{р 2} вычисляется в соответствии с (2) при a = к , где вместо m_р подставляется m_{р 2}.

Тогда выражение плотности вероятности оценки инварианта будет равно [4]

22 ( zx - т^)     ( x - m 2)

^               TZ2772

W (z )= f--------e 1 e 2 I x \Xx(9)

1 2naia2                         ,1

где о, = лDEZ ; a, = ЛDIZ ; m, = m ; m.= m

1          ^числ       2          ^знам 1 числ 2 знам

Расчет Р _пер проводится численно аппроксимацией формулы (9).

В системах с АМ и некогерентным приемом анало- гом вероятности попарного перехода является вероятность ошибки Рош, которая рассчитывается по известным формулам [3].

Вероятность попарного перехода и вероятность ошибки вычисляются для одинаковых значений h – отношения «сигнал/шум», котор ое вычисляется по формуле h = к " INV /о _р .

Пороговые значения z_p рассчитывалась путем минимизации Р _пер в формуле (3). Для k = 1 и INV₁ = 1, INV₂ = 2, 3, 4, 5, 6 вычисления дают результат z_p = 1,23; 1,49; 1,77; 2,07; 2,36. ^p

Для k = 0,7 и INV₁ = 1, INV₂ = 2, 3, 4, 5, 6 вычисления дают результат z_p = 1,14; 1,30; 1,50; 1,68; 1,92.

Результаты моделирования приведены на рис. 2 и 3, из которых видно, что особенностью любой инвариантной системы, основанной на принципе инвариантной относительной амплитудной модуляции является то, что по каналу передаются амплитудно-модулированные сигналы, образованные INV _l и S _об.

Передача этих сигналов обеспечивает на основе классических алгоритмов обработки информации, как правило, невысокую помехоустойчивость [3].

И только после обработки этих сигналов в соответствии с алгоритмом частного по выражению (4), получаем оценку инварианта, по сути являющуюся числом, а не сигналом.

Как видно из рис. 2 и рис. 3 вероятность попарного перехода одного инварианта в другой при больших отношениях «сигнал/шум» определяется величинами (10–30…10–40). При пересчете указанных выше величин вероятность ошибочного приема единичного символа в классических системах лежит в пределах (10–6…10–10).

Однако в реальных ситуациях точно определить значение коэффициента передачи канала связи нельзя. Следствием этого будет неточное определение порогов. Слагаемое знаменателя X_j формулы (4) оценки инварианта ИСПИ может быть представлено в виде

1 ^L

X j = 7 X( ^к Xi ^m , j ) ) , (10)

^L m = 1

где L – количество усреднений; k – коэффициент передачи канала связи; n ( m , j ) - j -й отсчет аддитивной помехи в m -й реализации сигнала обучения.

Тогда математическое ожидание X_j будет равно EX j = E ( к + n ( m , j ) ) = m ( к ) .

Кроме того, имеем следующее:

X = N ^X, = ^{m ( к} ) . к = g ⁽ X ) ,

$

где k – оценка коэффициента передачи канала связи; g – функция, обратная функции m .

По теореме об асимптотической нормальности g Ч X ) =

Dk ®⁽ g '( m ⁽ к ^{))) 2} Nl, m ( к ) = X , к = g ⁽ X ) , 11

( m ( к ) ) '    ^m ‘^{( к} ) ^m ‘⁽ g ⁽ X ) ) ^,

m ( к ) = о.

F ^- ^22 V( 2 i + 1 ) !! (к Y ⁱ e ^{2 о}

V 2       i ^^ ( i ! ) ² 4 i Ы

.

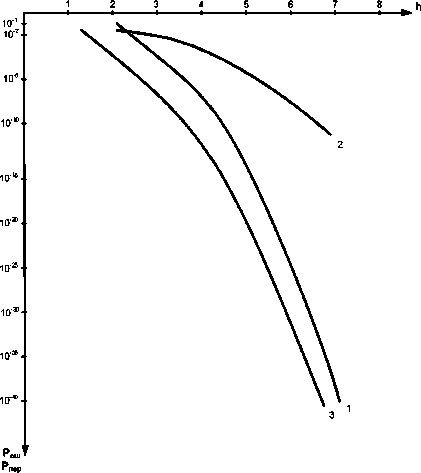
Рис. 2. Результаты моделирования: 1 – вероятность попарного перехода одного инварианта в другой при следующих заданных условиях: k = 1; INV₁ =1; INV₂ = 2, 3, … 6 и некогерентном приеме; 2 – вероятность ошибки при классической амплитудной модуляции и некогерентном приеме; 3 – вероятность попарного перехода одного инварианта в другой при следующих заданных условиях: k = 1; INV₁ = 1; INV₂ = 2, 3, … 11 и когерентном приеме

Тогда m,(к) = a ^2^

X

k

k ²

к - ^,(2 i + 1)!! Г к Y ^{i 2 0}

i = 0 ( i ! ) 4 ¹ v°7

a k2

“ ( 2 i + 1 ) !!2 i " к ² i ^{- 1}

⁺ e ²⁰ X -2T- i = 0 ( i ! ) 4 i a

$_a

Dk (m4k))2 N ■ L ’ k- = k - 3 \Dk ,(21)

k+= k + 3 VD^k .(22)

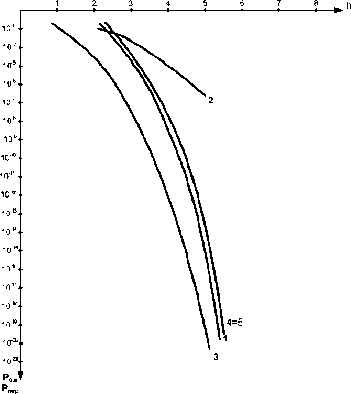
Рис. 3. Результаты моделирования: 1 – вероятность попарного перехода одного инварианта в другой при следующих заданных условиях: k = 0,7; INV₁ = 1; INV₂ = 2, 3, … 6 и некогерентном приеме; 2 – вероятность ошибки при классической амплитудной модуляции и некогерентном приеме; 3 – вероятность попарного перехода одного инварианта в другой при следующих заданных условиях: k = 0,7; INV₁ = 1; INV₂ = 2, 3, … 11 и когерентном приеме; 4 – вероятность попарного перехода при k = 0,7 и порогах, вычисленных при k _; 5 – вероятность попарного перехода при k = 0,7 и порогах, вычисленных при k ₊

Кривые 4 и 5 (рис. 3), соответствуют кривым помехоустойчивости при k _– и k ₊ соответственно. При этом Dk = 1,2 ■ 10 ¹⁹ , k_— =6,999 999 88 ■ 10^-1 и k + =6,999 999 89 ■ 10 - ¹. Как видно из этих кривых, наблюдается уменьшение помехоустойчивости ИСПИ.

Таким образом, предложена инвариантная некогерентная система передачи информации и определены ее качественные характеристики при неточном определении порогов.

Разработанный метод может найти применение в системах обработки информации.