Технологии интеллектуальных вычислений в ИТ-образовании: технологии дробных, мягких и квантовых вычислений и информационная сложность конечных объектов

Зрелов П. В., Зрелова Д. П., Тятюшкина О. Ю., Ульянов С. В. Технологии интеллектуальных вычислений в ИТ – образовании: технологии дробных, мягких и квантовых вычислений и информационная сложность конечных объектов // Системный анализ в науке и образовании: сетевое научное издание. 2022. № 3. С.110-137. URL:

INTELLIGENT COMPUTING TECHNOLOGIES IN IT EDUCATION: FRACTIONAL, SOFT AND QUANTUM COMPUTING TECHNOLOGIES AND INFORMATION COMPLEXITY OF FINITE OBJECTS

Zrelov Petr V.1, Zrelova Daria P.2, Tyatyushkina Olga Yu.3, Ulyanov Sergey V.4

1Head of the Scientific and Technical Department;

Joint Institute for Nuclear Research;

6 Joliot-Curie Str., Dubna, Moscow region, 141980, Russia;

Leading Researcher;

Plekhanov Russian University of Economics;

2Research Assistant;

Joint Institute for Nuclear Research;

3PhD in Engineering sciences, associate professor;

Dubna State University;

19 Universitetskaya Str., Dubna, Moscow region, 141980, Russia;

4Grand PhD in Physical and Mathematical Sciences, professor;

Dubna State University;

19 Universitetskaya Str., Dubna, Moscow region, 141980, Russia;

Chief Researcher;

Joint Institute for Nuclear Research;

6 Joliot-Curie Str., Dubna, Moscow region, 141980, Russia;

1.    Введение: цель и особенности применения технологии интеллектуальных вычислений в разработках процессов ИТ-образования

Итоги многолетнего (с 1991 г.) практического опыта промышленного применения программноалгоритмических продуктов для моделирования сложных систем мехатроники, робототехники и интеллектуальных систем управления в реальных проектах Yamaha Motor Co ., Ltd , ST Microelectronics , Siemens , Sony , Hitachi , Nippon Denso и др. выявили следующий факт. Инструментарий программных модулей интеллектуальных вычислений (типа Fuzzy Logic Toolbox , ANFIS , Robust Control и др.) в принципе не может решать корректно и эффективно задачи интеллектуального управления в условиях неопределенности и присутствия нештатных ситуаций [1] и часто не дает возможности достижения необходимого уровня робастности функционирования объекта управления даже в лабораторных условиях.

Причина заключается в отсутствии необходимого алгоритмического базиса интеллектуальных вычислений в структурах инструментария указанных модулей, что не позволяет решать задачи проектирования ИСУ с требуемым уровнем робастности [2]. Примеры сравнения результатов моделирования, например на оптимизаторе баз знаний (ОБЗ) на новых видах интеллектуальных вычислений, с упомянутыми модулями МАТЛАВ были проведены на т.н. типовых Benchmarks, которые наглядно показали высокую эффективность применения ОБЗ на мягких вычислениях в исследовании робастности ИСУ, функционирующих в непредвиденных ситуациях управления [1, 3].

Примечательным для данного результата является тот факт, что сравнение проведено студентами-бакалаврами в процессе дополнительного образовательного процесса по индивидуальным траекториям в рамках промышленного коммерческого проекта, потребовавший от студентов самостоятельного изучения технологии интеллектуальных вычислений нового вида. Самостоятельная работа трех школьников под руководством студентов-бакалавров и консультации доцента кафедры дала эффективные результаты по разработке автономного робота с нижним уровнем интеллекта на нечетком контроллера; доклад школьников на конференции среди магистров и преподавателей занял первое место; работа была написана школьниками и опубликована в полном формате [4].

Дополнительной причиной является отсутствие должного научного и материально-технического обеспечения учебно-образовательного процесса и соответствующей проблемно-ориентированной специализированной литературы (как зарубежной, так и отечественной).

Необходимость исправления недостатков и расширения возможностей инструментария типа МАТЛАВ / СИМУЛИНК при применении в процессах проектирования ИСУ объясняется дополнительным резким повышением сложности физических моделей традиционных ОУ, функционирующих в условиях непредвиденных ситуаций управления, а также исследованием новых моделей ОУ, разработанных на основе законов квантовой механики, теории относительности и термодинамики в квантовых сквозных ИТ. Процессы извлечения, обработки знаний и проектирования БЗ для такого рода ОУ требуют разработки новых видов наукоемких программно-алгоритмических продуктов ИТ [1], которые отсутствуют в программной среде МАТЛАБ, и успешно решаются на новых видах интеллектуальных вычислений [2, 3]. При этом качество извлеченных знаний и проектирование объективных БЗ находятся в прямой зависимости от точности и адекватности физической и математической модели ОУ [5, 6].

Следует также подчеркнуть, что стремительная смена элементной базы аппаратной поддержки и вычислительных средств на основе гибридных квантовых чипов позволяют существенно расширить прикладные области применения интеллектуальных контроллеров и встраиваемых ИСУ с ОБЗ на квантовых мягких вычислениях. Данные результаты составляют базис новой квантовой интеллектуальной ИТ проектирования робастных ИСУ и расширяют возможности применения инструментария MATLAB / SIMULINK при решении практических задач нового класса систем управления и системной интеллектуальной инженерии [7].

Цель и решаемые задачи . В статье целенаправленно рассмотрены основные определения, положения и принципы технологии интеллектуальных вычислений для применения в сквозных ИТ-образовательных процессах при подготовке специалистов нового поколения в области интеллектуальных сквозных ИТ и робототехники для проекта Индустрия 4.0. Рассмотрены трудно воспринимаемые ИТ-инженерией методологические вопросы теории качественных вычислений и приведены пути решения следующих задач: описание основных особенностей теории мягких вычислений и нечетких систем в ИТ-образовательных процессах в сочетании с решениями задач теории и систем управления; выделены трудные для инженерии моменты дробного исчисления и теории квантовых алгоритмов с позиции применения в проектировании интеллектуальных систем управления и когнитивной робототехники; обсуждаются вопросы выбора типа интеллектуальных вычислений для проектирования соответствующих алгоритмов управления в зависимости от сложности объекта управления; и приведено также сравнение полученных результатов с соответствующими результатами моделирования Benchmarks.

Опыт применения и реализации процессов ИТ-образования. Базисом и методологической платформой является указанный многолетний практический опыт подготовки квалифицированных кадров для промышленных компаний Yamaha Motor Co ., Ltd ( Iwata , Japan ) &  ST Microelectronics ( Milan , Сatania , Italia &  Grenoble , France ) &  Nippon Denso ( Nagoya , Japan ) при участии и поддержки университетов: University of Electro-Communications ( Tokyo , Chofu-shi , Japan ), Milan University ( Italia ), Nagoya University ( Japan ) и CA University ( California , San-Diego , USA ).

2.    Алгоритмическая и информационная сложности описания моделей конечных объектов

Выбор программно-алгоритмической платформы для анализа моделей объекта управления существенно зависит от алгоритмической и информационной сложности описания конечного объекта. Рассмотрим кратко основные положения теории сложности.

• 2.1.    Алгоритмическая сложность

Математические определения мер сложности алгоритмического описания конечного объекта по

Колмогорову K A ( x ( n ) n ) , по Шайтину C U ( n ) и по Коверу E U ( n ) формулируются следующим образом [8,9]:

K,(x ( n )| n ) = min l ( p ) ; С Л x ) = min l ( p ) ; E_TT(x ) = min l ( p )

A V V 71  7    A ( p , n )= x ( n )      7’ U V )   U ( p )= n            U\  )   U ( p )^ n

.

Здесь l ( ^p ) – длина последовательности p ; А рассматривается как вычислитель, p – как программа и x - выход. Рекурсивная функция A : { 0,1 } х N ^ { 0,1 } , где N — последовательность натуральных чисел; U : { 0,1 } ^ { 0,1 } .

По Колмогорову, сложность K ( X ) конечного объекта x определяется минимальным числом двоичных знаков (минимальной длиной программы l ( p ) ), содержащих всю информацию о задаваемом конечном объекте, достаточную для его восстановления. Сложность K ( x ) интуитивно определяет количество информации, необходимой для восстановления объекта x .

Существует связь между сложностью K ( x ) по Колмогорову и информационной энтропией

2 ^r

H ( qk )  следующего вида:  K(x)-< i(H(Як) + a(i)), где  H(Як) = —£Як log2 Як, a(i) = cr (Ini)/i, к=1

a ( i ) ^ 0, i ^ ^ . Следовательно, энтропия Шеннона – коэффициент при линейной части одной из частных мер сложности [9]. Для введенных мер сложности справедливы следующие соотношения:

E(x) + c0 < C(x) < E (x) + logl (x) + c; H (x) < M [C (x) |n] < H (x) + c;

K(x|l(x)) + c0 <

C (x) < K (x| (x)) + log K (x|l (x)) + log l (x) + c

Используя методы теории ценности информации и приведенные соотношения в [2] показано, что наиболее ценная информация дает минимальную сложность описания конечного объекта. В теории сложности, в свою очередь, показано [10], что эффекта понижения сложности можно достигнуть за счет расширения базиса, что позволяет в каждой практической ситуации соизмерять возможности имеющихся средств и сложность поставленных задач. Оценку изменения сложности выполнения поставленной задачи при использовании другого базиса можно получить, если хотя бы для одного из имеющихся базисов как набора средств известны оценки сложности.

• 2.2.    Информационная сложность и вычислительная точность аппроксимация описания конечного объекта

Конечные объекты управления представляют собой задачи в терминах математического программирования [11] следующего вида: f 0 ( x ) = min x E G C B n , f ( x ) <  0 ( i = 1,2,..., m ) . Предполагается, что G - замкнутое подмножество K ⁿ , f i ( x ) непрерывны на G . Множество конечных объектов управления Ы являются некоторым семейством задач заданного типа с общими G и m , и отождествляются с некоторым семейством Т непрерывных m + 1 -мерных вектор-функций на G , а объект управления с функцией f = ( f 0 , • • •, f_m ) . Здесь рассмотрим кратко вопросы реализации управления как численных методов [6,11]. Сущность численного метода заключается в последовательности наблюдений задачи f и последующем формировании результата. Последовательность наблюдений задачи f состоит в вычислении значений функционалов задачи и их производных в тех или иных точках G , а результатом может быть как точка G (приближенное решение задачи f ), так и ответ * о несовместимости f . Работа прекращается после выдачи результата. Управляющими воздействиями метода оптимизации при пошаговом наблюдении являются те точки, в которых наблюдались функционалы задачи. Сформированным результатом является управляющее воздействие на шаге, следующем за шагами-наблюдениями, а так называемый символ бездействия Ф выдается на всех последующих шагах как некоторое фиктивное управление. Формальное выражение реализации метода управления на задаче f как последовательности элементов имеет вид x 1 , x ₂,..., x i E X = G и {*} и { ф } . Последний член последовательности x ” , отличный от Ф , является результатом реализации x ^ю . Трудоемкость реализации x ” называется число отличных от Ф членов этой последовательности и равно числу шагов до выдачи результата.

Погрешность определяется как:

+^ , f совместна, x = * ;

^е ( ^x , f ) = '

= 0, f несовместна и x = * ;

m [ ( f ( x ) - f i . ) / r (. f ) i ]- в остальных случаях.

В (3) 0 <  г <  m и r i ( f ) > 0 - заданные нормирующие множители, f = ⁰ при i >  1 , ^f )_t равно оптимальному значению целевого функционала задачи f . Содержательная интерпретация (3) является следующая трактовка: если x е G используется в приближенном решении f , то его погрешность равна максимальному превышению функционалами задачи в точке x требуемых от истинного решения значений, а сами превышения измеряются в заданных единицах r i ( f ) . Невязка е ( X , f ) для точки x е G определяется по (3). Тогда по аналогии с (3) относительной погрешностью метода B^M на задаче f еЫ называется величина

+^ , если f совместна, X *( B M , f ) g* ;

V ( B ^M , f ) -<

0, если f несовместна, X * ( B ^M , f ) - { * } ;

sup { V ( x, f )| x G С П Х ’( B ^M , f ) } - в остальных случаях.

Относительная величина погрешности метода BM на классе Ы называется величина v ( B^M , ^) - sup { v ( B ^M , f )| f gU]

Потенциальные возможности методов решения задач Ы оценивается при помощи функций сложности классов Ы следующим образом:

N ( £ ) = inf { l |з B gB(U^) : l ( В, U^) < l, £ ( B,U ) < £ } , N ( £ ) = inf {l |з B g^c й: l ( B,U ) < l , £ ( B, W) < £ }

По (4) сложность N ( £ ) определяет минимальную трудоемкость, для которой найдется в общем случае стохастический Ы -метод. Для последнего выполняется точность £ в решении задач при указанной трудоемкости. Аналогично функция N ( £ ) определяет минимальную трудоемкость для детерминированных методов с фиксированной остановом.

Для (4) важное соотношение N ( £ ) <  N ( £ ) .

Примечание. Отметим, что множество ° - {to} сведений, которое может получить исследователь, задавая вопросы или ставя эксперимент, называется информационным пространством, а отображение ^: G xZ/ ^ 2° , ставящее в соответствие паре (X, f) множество ^ (x,f )*0 из ° - {to}, называется информационным отображением [11].

Информационная сложность класса Ы , отвечающая информационному отображению ^ и относительной погрешности v , определяется как функция

N_u ( v ) - 1 + inf { M |з B^M : v ( B^M , U ) <  v } - 1 + inf { M |v B^M : v ( B^M , U ) >  v }

Для оценки информационной сложности имеем [2,11]:

( 2 + 1        1 ^

Ig 2 k р (G) v k v            )

(       1 ^

< N_e ( V ) < I_G р ( G ) v k

V        v

где IG (§) - д -энтропия G и определяется при каждом 5 > 0 как наименьшее число точек G , таких, что замкнутые 5 -шары с центрами в этих точках покрывают все G .

В (5) нижняя оценка справедлива при любом локальном информационном отображении.

3.    Физическая строгость, математическая корректность и алгоритмическая сложность моделей конечных ОУ: взаимосвязь с технологией интеллектуальных вычислений

Обсудим, согласно [12], более глубокие механизмы разработки новых моделей интеллектуальных вычислений типа дробных исчислений, а также квантовых вычислений и проектирования процессов самоорганизации баз знаний (БЗ) на основе квантовых алгоритмов (КА), позволяющие расширить возможности проектирования ИСУ с более высоким уровнем робастности для слабо структурированных ОУ с плохо формализованной логической моделью физической интерпретации описания динамического поведения.

Примечание . В следующей работе авторов кратко описан разработанный инструментарий ОБЗ, позволяющий решить задачи ранее алгоритмически не неразрешимые в классической теории управления и теории интеллектуальных систем. К таким задачам относятся в первую очередь следующие: 1) оптимальное проектирование структуры нечеткой нейронной сети с наперед заданной точностью аппроксимации сигнала обучения; 2) проектирование требуемого уровня робастности; 3) определение оптимального числа продукционных правил и их внутренней структуры (конструирование универсального аппроксиматора); 4) выбор оптимального типа нечеткого логического вывода; 5) определение вида и оптимальных параметров функции принадлежностей в правилах « Если А То В» для типовой структуры нечеткого регулятора; 6) корректное тестирование робастности ИСУ и мн. др.

• 3.1.    Модели конечных ОУ и логические «парадоксы» технологии интеллектуальных вычислений

Разработка логически непротиворечивых и адекватных (корректных) физическим условиям и ограничениям математических моделей ОУ с целью объективного извлечения знаний из динамического поведения для эффективной реализации ИСУ новыми видами современной техники является одной из актуальных проблем для современного этапа развития теории и систем управления. Выбор корректной модели, в первую очередь ОУ минимальной алгоритмической сложности, является важной для практики задачей. Однако критерий минимальной алгоритмической сложности при выборе метода описания модели ОУ требует математического уточнения и физического обоснования [5, 6].

Отметим некоторые особенности технологии интеллектуальных вычислений и ее практического применения при формировании процессов ИТ-образования.

• А .    Системный анализ разработки и проектирования ИСУ. Построение корректных моделей для многих сложных ОУ тесно связано с необходимостью корректного учета существующих физических ограничений. Ограничения на описание динамического поведения сложного физического ОУ (в частности, на предельную точность процессов измерений и управления; выбор модели пространства -времени и др.) накладываются известными физическими законами (из таких дисциплин как статистическая механика, теория относительности, термодинамика, теория информации и квантовая механика).

• 3.1.1.    Влияние физических и логико-информационных ограничений на корректность математической модели

Примером таких ограничений являются следующие: 1) термодинамические ограничения на физическую реализацию математических моделей ОУ; 2) различные типы обобщенных информационных соотношений неопределенности Гейзенберга; 3) квантовые ограничения на пропускную способность передачи информации с учетом термодинамических флуктуаций; 4) квантовые оценки предельных возможностей точности измерений параметров ОУ и процессов управления в нанотехнологиях и мн. др.

Перечисленные физические ограничения должны быть учтены в алгоритме проектирования объективных БЗ в ИСУ.

Принципиальное значение при формировании корректных математических моделей имеет глобальная оценка функциональной реализуемости аппроксимации при наличии логикоинформационных границ и физических (термодинамических, квантово-релятивистских и др.) ограничений на описание реальных нелинейных физических ОУ. На основе достоверности извлекаемого количества информации определяется информационная оценка приращения риска (статистической корректности) формируемого описания модели ОУ и границ её применимости. Разработка логически непротиворечивых и адекватных (корректных) моделей ОУ с целью эффективной реализации интеллектуального управления новыми видами современной техники является одной из актуальных проблем для современного этапа развития теории и систем управления.

Введение понятий синергетики динамического поведения, релятивистской и квантовой теории для учета физических особенностей ОУ в ряде случаев позволяет существенно повысить качество описания соответствующих моделей [5].

Рассмотрим в связи с отмеченным фактом некоторые примеры.

Пример 1: Квантовые ограничения и корректность идентификации моделей ОУ. В общей теории динамических систем в ряде случаев оптимальные статистические процедуры для Гауссовских случайных полей оказываются, как правило, линейными. Для стационарных полей линейные статистические задачи приводят к исследованию уравнений Фредгольма 1-го рода типа

t

y(t) = Jk(t-s)x(s)ds,   t e[0,T], [x,y] = 0

, и являются для идентификации ОУ или его входного сигнала [ x (t), k (t) ] некорректными задачами по Тихонову. Учет квантовой природы описываемых полей (например, бозонных) приводит к рассмотрению интегрального уравнения Фредгольма 2-го рода типа [13]:

t

y (t) = —x(t)+ J k(t -s)x(s)ds, t e [0,T], [x,y] = ih

2      0

,

где – постоянная Планка. Таким образом, учет квантовой природы физического поля (квантовые ограничения в виде некоммутативности наблюдаемых) приводит к естественной регуляризации некорректных задач, исследуемых в теории управления традиционными ОУ.

Рассмотрим теперь на примерах какие информационные–термодинамические ограничения могут быть наложены на модели ОУ.

Пример 2. Информационные оценки приращения риска и корректности описания статистических моделей ОУ. Рассмотрим типовую ситуацию идентификации слабо формализованной модели структуры ОУ в виде случайных параметров x = (x1,...,xn) в присутствии (мешающего или маскирующего) параметра θ . Допустим, что экспериментально (в статистическом смысле) для вектора измеряемых случайных величинx = (x1,...,xn) и неизвестного параметра 9 определена функция плотности распределения вероятностей параметров модели в виде p (x, 9) (аппроксимирующая в общем случае неизвестную истинную функцию p (x, 9)). Информационное расхождение (дивергенция) между функциями распределения вероятностей определяется мерой Кульбака-Лейблера в виде:

Р(x’9)^             .              wlw\                         „ p (x, 9) ln— ---- dxd9. По заданным функциям потерь W (W) и распределения вероятностей

Р (x, 9)                                                        х 7

Р ( x,⁹ ) [ ^p ( x , 9 ) J          вычисляется         усредненный         риск         в         виде:

r ( W² ) ( r ( W ² ) ) = JJ W²Р ( x,9 ) dxd9 ( JJ W²p ( x , 9 ) dxd9 ) . Тогда информационная оценка приращения риска (снижения точности определения параметров модели ОУ из-за редукции аппроксимации истинной функции плотности распределения вероятностей, как меры корректности модели) определяется следующим выражением [14]:

^-^/ r ( ^{W 2} ) ² I ( p : p ) <  ( 5 = r - r ) < ^ r ( W ²) 2 I ( p : p )

Таким образом, (верхняя и нижняя) оценка корректности модели в виде приращения риска ( 5 = r - r ) из-за редукции данных измерения при мешающих параметрах в процессах измерения носит нелинейный характер зависимости от информационной дивергенции – расхождения (меры информированности исследователя) оценок качества модели ОУ. Приведенный результат означает, что исходного количества информации и интуитивного представления в виде информированности исследователя может оказаться недостаточным для формирования корректной модели ОУ, а сформированная модель содержит структурные элементы неопределенности.

Следовательно, интуитивный инженерный подход к разработке приближенных (расчетных) моделей ОУ, носящий зачастую вид линейной зависимости от количества извлекаемой информации о параметрах структуры ОУ, может привести к существенному расхождению в точности и с необходимым качеством формирования корректного описания модели ОУ [2, 3].

Приведенный пример показывает, что помимо физических ограничений, на корректность описания и достоверность извлеченных знаний из модели ОУ существенное влияние оказывают также и информационные границы на применимость разработанной модели. На основе достоверности извлекаемого количества информации определяется информационная оценка приращения риска (статистической корректности) формируемого описания модели ОУ, и границ её применимости. В результате методология оценки корректности математических моделей слабо структурированных физических ОУ находится в стадии своего становления и требует привлечения новых видов интеллектуальных вычислений, способных установить причинно-следственные связи и взаимоотношения подсистем.

Таким образом, выбор физически строгого базиса и математически корректного способа определения критерия описания конечной модели объекта управления (ОУ) с требуемой точностью существенно влияет на качество процесса извлечения объективных знаний из динамического поведения ОУ и на формирование робастных баз знаний (БЗ) в интеллектуальных системах управления (ИСУ).

Б . В теории и систем управления одним из эффективных подходов снижения риска принятия решения (от неполноты описания модели ОУ и внешней среды) является разработка структур робастных ИСУ. Данные структуры реализуют принцип компенсации неопределенности описания модели ОУ за счет повышения уровня интеллектуальности традиционных систем управления. В частности, компенсация информационной неопределенности осуществляется за счет повышения интеллектуальности нижнего исполнительского уровня в виде соответствующих структур интеллектуальных регуляторов и соответственно спроектированных самоорганизующихся робастных БЗ. Неизмеримые (ненаблюдаемые) обобщенные координаты динамического поведения ОУ или скрытая в классических состояниях квантовая информация в законах управления ИСУ, существующая в силу квантовой нелокальной корреляции, являются одним из примеров такой ситуации управления. Подобные эффекты должны быть учтены и скомпенсированы продукционными логическими правилами в соответствующих БЗ проектируемых робастных ИСУ. Поэтому принцип компенсации неполноты описания модели физического ОУ разработкой и применением соответствующего уровня интеллектуальных вычислений является одним из основных при исследовании слабо структурированных моделей ОУ [2].

• В .    Применение новых технологий в инженерной практике теории и систем управления часто сталкивается с проблемами преодоления инерции «прагматической» инженерной интуиции и философии системной инженерии. Так происходило, например, в начале 70-х прошлого столетия при внедрении в инженерную практику идей мягких вычислений на основе теории нечетких множеств (см. первую в мировой практике книгу по проектированию нечетких систем управления [2] - авторы являются одними из пионеров в этой области) в процессы проектирования нечетких регуляторов и систем управления. Суть возникающих «парадоксов» заключается в физической и логической интерпретации понятия числа, производной и интеграла как исходного базиса моделирования ОУ и проектирования систем управления. Поясним данный факт наглядными примерами, которые позволяют установить причинно-следственные связи и обоснование результатов физической интерпретации возникающих мнимых логических «парадоксов». Например, понятия производной и интеграла нецелочисленных (дробных) порядков, лежащих в основе дробного исчисления, при первом знакомстве с ними вызывают существенные затруднения при попытке их наглядной геометрической и корректной физической интерпретации, которые препятствуют широкому использованию этого исчисления в прикладных областях исследований и разработок робастных систем управления.

Достаточно отметить, что в зависимости от определения производной нецелочисленного порядка, применение производной такого типа к постоянной величине приводит к «парадоксу» - результат отличен от нуля. Хотя история возникновения и развития дробного исчисления насчитывает уже более трех столетий, его основы не изучаются в большинстве курсов математического анализа технических университетов. Между тем, существо перехода от классического математического анализа к его обобщению, которым и является дробное исчисление, может быть достаточно просто изложено с помощью приемов, уже известных в математике (см. ниже, п. 4).

Г . В традиционных исчислениях по количественному результату численного алгоритма осуществляется соответствующая оценка качественного свойства исследуемого объекта. Логическая оценка качества в общем случае может быть осуществлена только в конце количественных вычислений, а для алгоритмически неразрешимых численных проблем (сложность алгоритма по Колмогорову), часто искомая оценка не может быть достигнута. Основой интеллектуальных вычислений является возможность применения операций не только на числовых шкалах (как в традиционных

Сетевое научное издание «Системный анализ в науке и образовании» Выпуск № 3, 2022 год вычислениях), но и введение новых видов операций на шкалах, определяющих качественные характеристики исследуемого объекта. В этом случае, цель применения интеллектуальных вычислений заключается в реализации возможности непосредственного определения качественных характеристик объекта, оперируя алгоритмически последними также как на числовых шкалах. Количественные оценки объекта можно получить из качественных оценок обратным отображением шкал.

Мягкие и квантовые вычисления являются примерами таких исчислений.

Большим сюрпризом применения КА оказался выявленный эффект, что при этом многие классические задачи могут быть решены с экспоненциальным ускорением или решены алгоритмически принципиально неразрешимые классическими методами задачи. Так, например, для определения качественной характеристики функции (постоянная или балансирующая для четырех аргументов) в традиционном подходе требуется четыре шага численных операций, в тоже время квантовый алгоритм Дейча (1985 г.) определяет данное качество исследуемой функции за один шаг. Алгоритм Шора решает задачу факторизации заданного числа с экспоненциальной скоростью по отношению к лучшему известному алгоритму, а при увеличении длины решает алгоритмически неразрешимую задачу с полиномиальной сложностью. Алгоритм Гровера осуществляет поиск решения в неструктурированных данных с квадратичной скоростью.

Нечеткие множества, введенные в 1965 г. Л. Заде, позволяют расширить (многовековое) определение самого числа и ввести множество новых шкал качественных характеристик, которые невозможно определить методами классических исчислений. Но при этом многие «парадоксальные» факты интерпретации результатов применения нечеткой логики основаны на отказе от закона булевой логики в виде закона исключения третьего.

Квантовая логика приводит к обнаружению скрытой квантовой информации в классических логических операциях при применении к ним нелинейных преобразований.

Такие исчисления открывают новые возможности для теории и проектирования ИСУ. В частности, применение данных типов вычислений или их совместных комбинаций существенно повышают уровень робастности ИСУ, функционирующих в условиях информационного риска или непредвиденных (нештатных) ситуациях. В результате существует понятие физической и математической корректности описания ОУ, а также применяется понятие физической, математической и расчетной модели ОУ [2, 5, 6]. Поэтому рассмотрим предварительно методы учета качественных особенностей построения корректных моделей ОУ следуя [2]. Обсудим также их взаимосвязь с моделями интеллектуальных вычислений, таких как мягкие, дробные и квантовые вычисления в задачах проектирования робастных ИСУ [1, 2]. Параллельно рассмотрим подробно роль возникающих мнимых «парадоксов» при их применении в интеллектуальной системной инженерии.

В первую очередь, рассмотрим кратко методологические особенности применения технологий мягких, дробных и квантовых вычислений, используемых при проектировании робастных БЗ ИСУ.

4.    Технология мягких вычислений

Логический «парадокс» в виде обобщения понятия числа за счет введения субъективной качественной шкалы (и отображения в нее в виде лингвистической переменной качественной аппроксимации его количественной характеристики) привело к нарушению логического закона «исключение третьего» и к более 30-летней дискуссии с представителями научной школы теории вероятностей. К таким трудностям относится, например, корректное определение понятий функции принадлежности, логические взаимоотношения «нечеткая/случайная величина» и др. Основой технологии мягких вычислений являются теория нечетких множеств и модели нечеткой логики , в которой, как отмечалось выше, не используется закон исключения третьего . Это приводит к нестандартному выводу о возможности одновременного рассмотрения, например, числа 10 на шкале [0, 100] как лингвистической переменной « большой » или « маленький » с различными значениями функции принадлежности на заданной качественной лингвистической шкале. Трудность определения самой функции принадлежности было возложено на эксперта, что приводило к введению субъективных факторов в математические модели и вызывало критику со стороны представителей вероятностной школы исследования неопределенностей. В теории случайных процессов с помощью решения уравнения Фоккера-Планка-Колмогорова можно по входным данным и характеристикам динамической системы определить функцию плотности распределения вероятностей выходного сигнала, которая является полной

Сетевое научное издание «Системный анализ в науке и образовании» Выпуск № 3, 2022 год его объективной характеристикой. В теории нечетких систем технология определения функции принадлежности (аналогичной теории случайных процессов) отсутствовала.

Только практическое применение нечетких САУ классическими ОУ разъяснило и сняло разногласия и трудности определений индивидуальных и массовых событий, операции осреднения и извлечения информации и т.п. [1, 2]. В результате нечеткие модели логического вывода на фазовом пространстве лингвистических переменных позволили разработать структуры нечетких ИСУ, эффективно решающие задачи управления в условиях существенной неопределенности исходной информации, слабой формализации описания ОУ и нечеткости целей управления.

Одной из основных проблем практического и эффективного применения технологии мягких вычислений в задачах интеллектуального управления являлось решение следующих задач: а) объективное определение вида функции принадлежности из заданного класса и ее оптимальных параметров в продукционных правилах БЗ; б) определение оптимальной структуры нечетких нейронных сетей (ННС) в задачах обучения (аппроксимация обучающего сигнала с требуемой/заданной ошибкой и с минимальным количеством продукционных логических правил в БЗ – разработка и проектирования универсального аппроксиматора; в) применение генетического алгоритма (ГА) в задачах многокритериального управления и наличии дискретных ограничений на параметры объекта управления и др.

Такие задачи, как отмечено выше, принципиально не решаются инструментарием Fuzzy Logic Toolbox и Robust Control, встроенных в виде автономных модулей в среду MATLAB .

Перечисленные проблемы были решены и апробированы на основе разработанного оптимизатора БЗ (ОБЗ) с применением технологии мягких вычислений. Разработанный интеллектуальный инструментарий позволил проектировать робастные БЗ на основе решения одной из алгоритмически трудно решаемых задач теории искусственного интеллекта – извлечения, обработки и формирования объективных знаний без использования экспертных оценок [15-17].

В структуре оптимизатора используются три генетических алгоритма (ГА), которые позволяют спроектировать, как следствие, оптимальную структуру нейронную нечеткую сеть -ННС - (вид функций принадлежности и их параметры, количество внутренних слоев и др.), аппроксимирующей обучающий сигнал с требуемой (заранее заданной) ошибкой. Объединение методологии стохастического и нечеткого моделирования ИСУ в инструментарии разработанного ОБЗ позволило повысить уровень робастности проектируемых БЗ и решать сложные задачи формирования объективных знаний [16].

Однако, при существенном изменении среды функционирования или при возникновении непредвиденных ситуаций управления, спроектированные законы управления не всегда гарантируют требуемые условия робастности и, соответственно, достижение цели управления. Данный эффект ограничивается функциональной структурой ГА, в которой (по определению) пространство поиска решений фиксировано и задается экспертом, а также выбором функции пригодности, которая рассматривается как критерий оптимального управления.

Таким образом, найденное технологией мягких вычислений (на основе ГА) оптимальное решение соответствует только заданной ситуации управления, содержит (в неявном виде) субъективность исходной информации, а при неправильном определении пространства поиска найденное решение может неадекватно соответствовать ситуации управления. Для такого рода ситуации управления требуется привлечение новых видов технологий интеллектуальных вычислений, такой как, например, технология интеллектуальных квантовых вычислений [18-20].

Следует отметить, что технология мягких вычислений уже эффективно применяется в задачах управления квантовыми ОУ. Однако до настоящего времени применение квантовых вычислений для эффективного решения классических алгоритмически неразрешимых задач теории и систем управления сталкивалось с утверждением Ю. Манина и Р. Фейнмана (введенного в начале 80-х прошлого столетия) о необходимости применения квантовых вычислений к решению квантовых задач.

5.    Технология квантовых вычислений

В квантовой логике технологии интеллектуальных квантовых вычислений и квантовой теории информации существует «парадокс» – не выполняется классический закон дистрибутивности. Этот факт отражает новые (необычные) явления в квантовой механике типа некоммутативности переменных, неопределенности и невозможности одновременного точного измерения наблюдаемых и др. В результате необычные явления для классической физики, такие как запутанные состояния (entanglement), телепортация, сверхплотное кодирование приводят к «парадоксам» и трудностям физической интерпретации с позиции логики классической физики. Так, например, две подсистемы, каждая из которых находится в смешанном хаотическом состоянии (и с отличной от нуля энтропией), при слиянии в единую систему образуют чистое (с нулевой энтропией) состояние, обладающее высшим уровнем порядка (эффект квантовой самоорганизации). При этом количество информации в целой системе меньше, чем в каждой из её составляющих подсистем, а взаимная энтропия имеет отрицательное значение.

Квантовая суперпозиция, состоящая из двух классических взаимоисключающих логических состояний, позволяет образовать одно единое состояние, содержащее, например, одновременно логически противоречащие «да» и «нет» (состояние типа «кот Шрёдингера»). Из двух классических однобитовых состояний с помощью квантовой корреляции (которая выше классической) возможно дополнительно (в зависимости от вида квантовой коммуникации) извлечь еще более одного бита. Квантовые стратегии принятия решений позволяют из двух классических игроков, не имеющих стратегий выигрыша в данной игровой ситуации, сформировать игрока-победителя (« Паррондо » эффект), использующего квантовый подход к решению задачи.

Рисунок 1 демонстрирует физическое различие в определении вычислительного базиса мягких и квантовых вычислений.

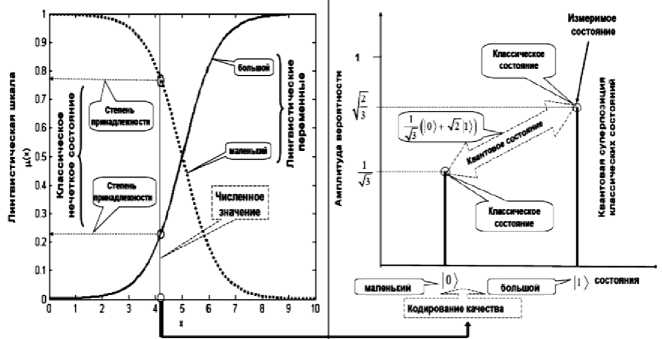
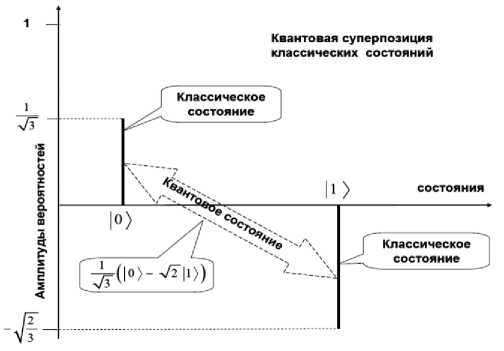
Рис. 1. Физическое различие между нечетким и квантовым состояниями

Одновременно рис. 1 дает корректную физическую интерпретацию значения квантовой суперпозиции (quantum superposition) с различными классическими состояниями типа: -1=(| 0^ + V2|1) ) и -1 (| 0) - V2|1) ) (квантовые состояния - quantum states), соответственно.

Из представленных на рис. 1 описаний физических состояний видно, что нечеткое состояние числа имеет два значения функции принадлежности на шкале лингвистического описания (принцип

Сетевое научное издание «Системный анализ в науке и образовании» Выпуск № 3, 2022 год исключения третьего не выполняется). Квантовое же состояние состоит из двух классических состояний, качественные характеристики которых закодированы в квантовых переменных, связанных принципом квантовой логической дополнительности.

Совместное использование вычислительных базисов из рис. 1 приводит к новому виду квантовых мягких вычислений [20].

Таким образом, описание на квантовом языке постановок многих классических (слабо структурированных) инженерных задач (трудно решаемых на языке классической логики) позволяет найти их эффективное решение. Однако такой подход имеет ряд особенностей при практическом применении в задачах управления. В теории квантовой информации и квантовых вычислений понятию числа соответствуют понятия наблюдаемой и суперпозиции состояния наблюдаемых квантовой системы, а необратимое измерение дает одно из возможных состояний.

Положительные результаты применения классических технологий интеллектуальных вычислений (типа мягких вычислений) совместно с аппаратом квантовых вычислений привело к новому альтернативному подходу – применению технологии квантовых интеллектуальных вычислений в задачах оптимизации процессов управления классическими ОУ (физический аналог применения обратного метода исследования « квантовая система управления – классический ОУ»). Такой подход также существенно расширяет возможности самих интеллектуальных вычислений.

6.    Дробное исчисление (fractional calculus)

Математический анализ с использованием интегро-дифференциальных операторов нецелых порядков или дробное исчисление (fractional calculus) имеет более чем трехвековую историю. Здесь рассмотрим только некоторые характерные примеры [1,21]. Обсудим, в частности, аналоги функций в классическом математическом анализе с точки зрения дробного математического анализа. Такие аналоги являются обобщением известных функций в классическом математическом анализе и наглядно иллюстрируют «парадоксы» дробного исчисления с точки зрения операций и результатов стандартной интерпретации математического анализа.

Прежде всего, рассмотрим аналог известной формулы дифференцирования для степенной функ- ции порядка n в виде:

dⁿx ( t )      _{z x z}            k к !

----P = к ( к -1 )-«-( к - n +1 )------- t dtⁿ                               ( к - n ) !

. Анализ приведенной формулы для

производной порядка n показывает, что формально порядок дифференцирования может быть отличным от целого. Для этого необходимо использовать Гамма-функцию, которая обобщает факториал-функцию на случай нецелочисленных аргументов. Гамма-функция для целых положительных x = n связана с факториалом в виде Г ( n ) = ( n - 1 ) ! . Выполнив замену целого порядка дифференцирования n на дробный в и вводя, Гамма-функцию, получим следующую формулу дифференцирования степенной функции с дробным порядком:

dвx(t) _  Г(к +1)

dt ^в     Г ( к - в +1 )

Так, например, для единичной функции типа f (x) = 1 в стандартном математическом анализе df ( x )

производная имеет вид ----- = — = 0.

dxdx

Однако в дробном исчислении согласно (6) дробная производная имеет вид d в f ( x) _ d в1 _ dxe     dxe   Г(1 - в)

для всех значений в .

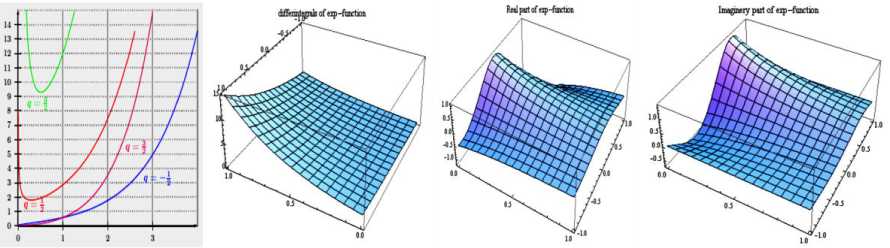
Выражение (6) может рассматриваться как функция трех аргументов: t, k и β; таким образом, дается более подробное описание функции и всех ее производных и интегралов (как целого, так и дробного порядков). В качестве иллюстрации приведем графические образы выражения (6) для случаев k = 0, когда порядок дифференциального оператора изменяется в пределах от -1 до +1.

Рис. 2 показывает [21] изменение дифференциала для данного случая.

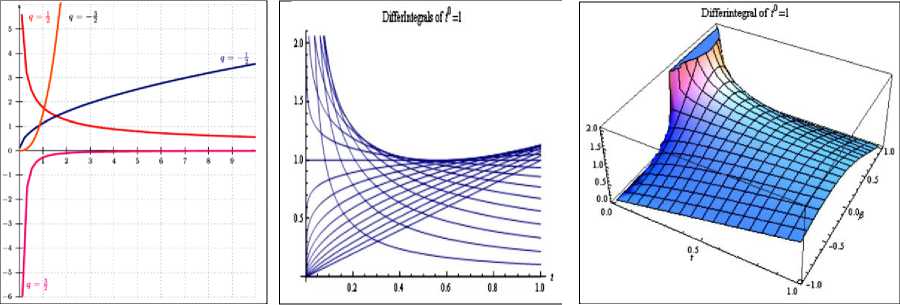
а)                                 б)                                   в)

Рис. 2. Графики дифференциалов от единичной функции для различных значений в = q = 1/ 2,3/ 2, -1/2, -3/2 (а); в пределах -1 < в < +1 (б); и изменение дифференциала в 3D как функции параметров (t, k = 0, в) (в)

df ( x )  dx dx " dx " "

Для идентичной функции f (x) = x имеем d f (x)   dqx     x1q

В то время как дробная производная ---"— = —- = —:----г .

dx      dx   Г( 2- q)

На рис. 3 показаны графики дробных дифференциалов для различных значений в = q = 1/2,3/2, - 1/2, - 3/2 .

Для экспоненты

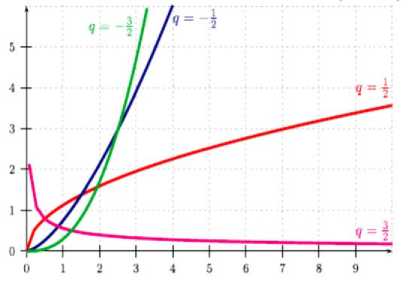
Рис. 3. Графики дифференциалов от идентичной функции для различных значений в = q = 1/2,3/2, - 1/2, - 3/2

f ( x ) = e x дифференциал определяется в виде

d V x dx^q

го

=Е

k = 0

x^{k - q}

Г(k - q +1)

На рис. 4 показаны графики рассмотренных дифференциалов от указанных функций.

а)                          б)                   в)                               г)

Рис. 4. Графики дифференциалов от экспоненциальной функции

Таким образом, дробное исчисление относится к обособленному разделу математического анализа и является инструментом математического моделирования сложных динамических процессов в обычных и фрактальных средах. Данный математический инструментарий позволяет решать на новой основе понятия производной и интеграла задачи анализа, синтеза, идентификации, диагностики, создания новых типов робастных систем управления.

• 6.1.    Особенности теории дробных вычислений

Отмеченная ранее особенность вычисления дробных производных и интегралов, выраженная в непривычной форме интерпретации результата, отразилась на длительности интервала времени применения методологии дробных исчислений в практике инженерных исследований. Вызывали трудности решения вопросов выбора модели дробной производной и дробного интеграла, выбора метода численного метода моделирования, определения оптимальных значений дробных показателей и коэффициентов усиления регуляторов, определения дробных случайных процессов и дифференциальных уравнений для описания модели ОУ, и мн. др.

Только за последние 20 лет данное исчисление приобрело новое интенсивное развитие в связи с появлением практических инженерных приложений. В отличии от стандартного определения производной функции от аргумента, которая определяется в данной точке, производная дробного порядка зависит от памяти предыдущих состояний. Для избежания многих «парадоксов» и необходимости иметь корректные предельные переходы к классическому определению, было предложено множество моделей интегродифференциалов и дифферинтегралов, выбор которых определялся возможностями корректных схем численного интегрирования и конкретными условиями описания модели ОУ.

Выше было рассмотрено представление производной в виде прямого обобщения показателя производной на нецелочисленный случай. Рассмотрим для сравнения другой вариант определения дробной производной в виде модели Эллиотта [22]:

D a У ( x ) =------- f --------- У ( x ') dx\ ^a , x ^E®                                                    (7)

• * ⁽ )    1 ( a ) " ( x - x ') “ ⁽ )     ,     ,        +                                                                       '

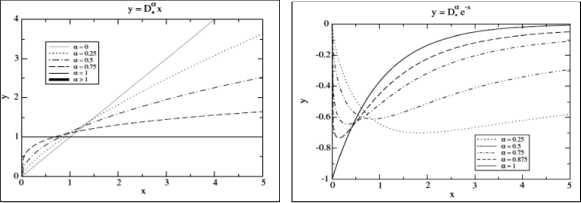
Результаты численного интегрирования (7) для функций y (x) = x и У (x) = e x представлены на рис. 5 а, б соответственно.

а)                                                       б)

Рис. 5. Примеры вычисления дробных производных y ( x ) = x и y ( x ) = e

— x

Сравнение с результатами, представленных на рис. 5, а,б показывает существенные различия в качественном поведении вычисленных функций. В частности, на рис. 5 а представлены три D 0 У ( x ) = x , D * У ( x ) = ¹     D* У ( x ) = °, ^v ^ >  1

специальных случая:  ★          ★        и ★              , которые не противоречат резуль- а = %, %, % татам математического анализа. Промежуточные значения            имеют плавные переходы в

а = 0

промежутке между значениями      и 1, что согласуется с интуитивным представлением о каче ственном поведении производной.

Качественной поведение производной от экспоненциальной функции имеет скачкообразный характер, стартуя из нуля, резко пересекает график стандартной производной и стремится затем к нулевому значению. Отмеченные особенности проявляются в процессах численного интегрирования дифференциальных уравнений дробного порядка.

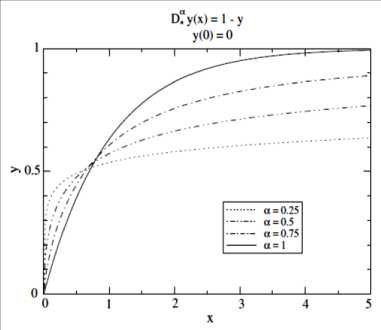
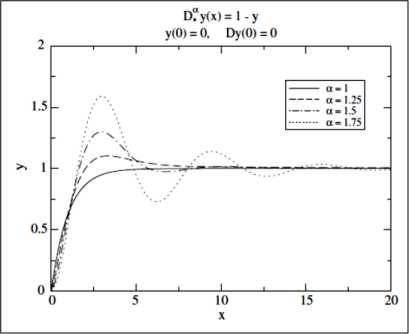
На рис. 6 приведен пример численного интегрирования дифференциального уравнения дробного порядка следующего вида: D ^ У ( x ) = 1 - У ( x ) при разных значениях а и разных начальных условиях.

а)

б)

Рис. 6. Динамическое поведение системы D 0 у ( x ) = 1 - у ( x ) при различных а е ( 0,1 ] и начальных условиях у ( 0 ) = 0 (а) и а е [ 1,2 ) , и начальных условиях у ( 0 ) = 0 , Dy ( 0 ) = 0

При этом вид качественного поведения и математическое описание свойств самой гамма функции Эйлера представляют самостоятельный интерес.

В общем виде гамма функция имеет следующий вид:

^Г ( x M

J e t t x ¹ dt , Re ( x ) >  0

I x - 1 n ! n lim ————— -----, ^{( x - любое})

^ n ^_ю x ( x + 1 )( x + 2 )...( x + n - 1 )

.

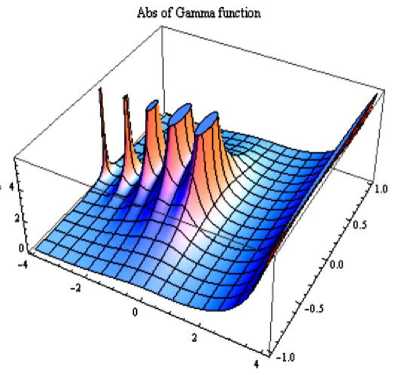
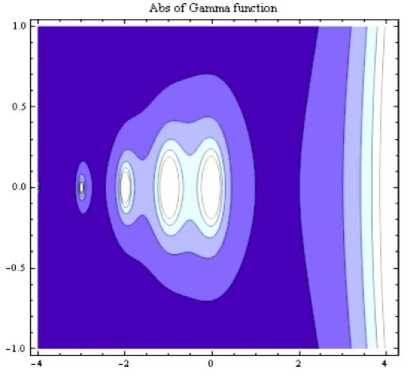
На рис. 7 и 8 представлен вид модуля Гамма-функции комплексного и Гамма-функции действительного аргументов.

а)                                                        б)

Рис. 7. Вид гаммы функции: а) - модуль Гамма-функции комплексного аргумента; б) - модуль Гамма-функции комплексного аргумента (контурный график)

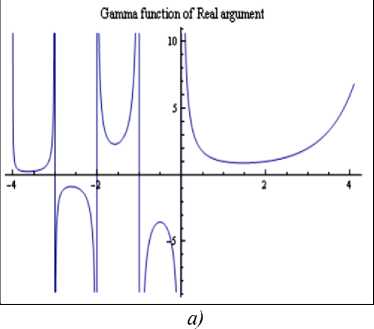
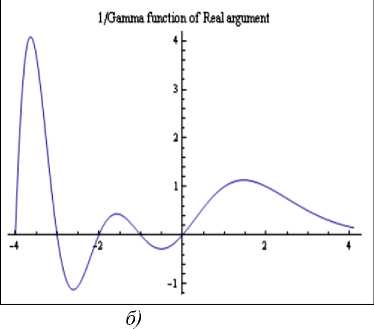
Рис. 8. Вид Гамма-функции действительного аргумента: а) - Гамма-функция действительного аргумента; б) - обратная Гамма-функции действительного аргумента

На рис. 8 видно, что Гамма-функция претерпевает разрывы вида ± ∞ в нуле и при целых отрицательных значениях аргумента. Однако, в дробном анализе чаще всего встречаются значения Гамма-функции в степени ( - 1) или отношения Гамма-функций различных аргументов, которые являются непрерывными функциями на множестве рассматриваемых значений аргументов.

Для примера на рис. 8,б показан вид функции 1/Γ( x ), которая является непрерывной функцией. Таким образом, описание и моделирование ОУ существенно зависит от модели дробной производной, начальных условий, метода интегрирования, выбранного порядка производной и т.п. Данные вопросы и их роль в задачах моделирования ОУ и робастного управления рассмотрены в Части 2.

Практика применения данного исчисления, например, в задачах робастного управления, показала его эффективность, что привело к планомерному его исследованию в задачах теории и систем управления.

• 6.2.    Роль дробных вычислений в интеллектуальном робастном управлении

Применение методов дробного исчисления в задачах робастного управления дали возможность повысить качественные характеристики процессов управления. Так, например, на рис. 9 показан переходной процесс ПИД-регулятора и дробного ПИД-регулятора на ступенчатое воздействие [23].

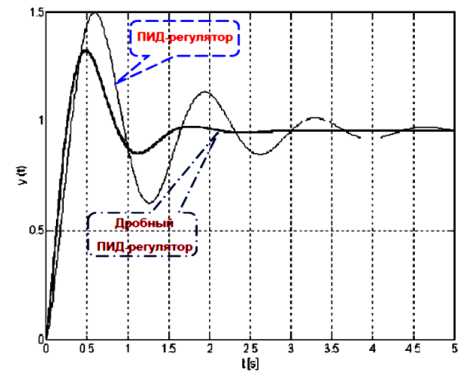
Рис. 9. Сравнение переходных процессов ПИД-регулятора и дробного ПИД-регулятора на ступенчатое воздействие

Нетрудно заметить, что динамические характеристики дробного ПИД-регулятора (перерегулирование, время переходного процесса, точность, ошибка управления) значительно лучше традиционного ПИД-регулятора. Однако форма дробного интегро-дифференциального исчисления приводит к новым трудностям разработки методов аналитического и численного исследования динамического поведения таких регуляторов.

Достаточно отметить здесь, что применение дробного исчисления к структуре традиционного ПИД-регулятора типа:

ПИД = k_p + k_Ds + k_fs ¹ = k_pe + k_De + k_z J e ( т ) dт

Частотная область               Временная область существенно изменяет структуру регулятора, например, для PI q2 Dq и qx = _, q2 = - _ имеем:

• - ¹      '                  + q           - q                               1 Г e ( т )                    1 г e ( т )             П !

PI 2 D 2 = kp + kDs  1 + kts  2 ^ kp (t)e + kD (t) —=■ J  / dт + kt (t) —= J  ,     dт—------—

'---------v--------- *                    ^П 0 ^t - т           фо о Nt - т Г ! ( n - r ) !

Частотная область

Временная область

В теории и проектировании систем управления на основе дробных вычислений эффективно используются также необычные для традиционных структур регуляторов такие как I ^{- q 2} D q , т.е. дробные интегро-дифференциальные регуляторы.

На рис. 10 показано сравнение динамического поведения дробного I ^{q 2} D q ¹ регулятора с поведением дробного PI (ПИ), PI (ПИ) и PID(ПИД) на ступенчатое возмущение.

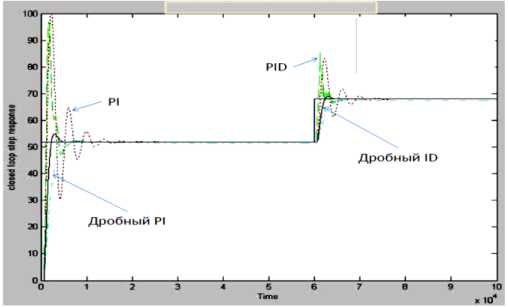
Рис. 10. Сравнение динамического поведения дробного I ^{q 2} D q регулятора с поведением дробного PI (ПИ), PI (ПИ) и PID(ПИД) на ступенчатое возмущение

Из результатов сравнения динамических характеристик видно превосходство I - q ² D q регулятора. В то же время, ПИД-регулятор дробного порядка теперь имеет пять параметров { k P , k^D, k¹, q^v q ² } и позволяет существенно расширить область поиска оптимальных параметров по сравнению с традиционным ПИД-регулятором для достижения области робастности ИСУ [24, 25].

Использование мягких и квантовых вычислений в сочетании с моделями дробных регуляторов с нечеткими регуляторами, со скользящим режимом, нечетких Н / Н^ -регуляторов, а также методов PSO (particle swarm optimization) и др. расширяет возможности процессов проектирования робастных ИСУ.

На рис. 11 показано cравнение динамического поведения дробного ПИД-регулятора, спроектированного методом PSO, с Н ₂ / H -регулятором и Н _у -регулятором [25].

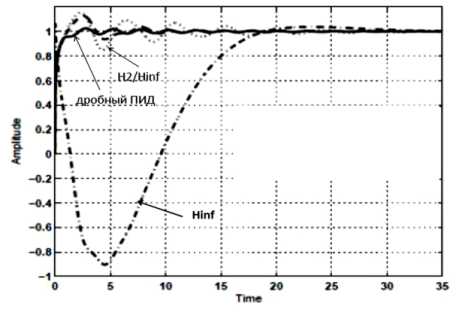
Рис. 11. Сравнение динамического поведения дробного ПИД-регулятора с Н^ / Н -регулятором и Н -регулятором

Из результатов сравнения следует преимущество дробного ПИД-регулятора. Данные и другие типы регуляторов, а также смежные вопросы дробного исчисления и их совместное использование с интеллектуальными вычислениями рассмотрены в следующей работе авторов.

7.    Особенности квантовой логики вычислений

В классической логике выполняются законы коммутативности, ассоциативности, упорядоченности, поглощения и имеет место дистрибутивный закон ( A + B ) C = AC + BC . Переменные A,B,C ,... называются высказываниями. Между некоторыми парами высказываний A,B,C,... можно установить отношение порядка A <  B означающее, что если высказывание A истинно, то высказывание B также истинно, или высказывание B является следствием высказывания A . В квантовой логике также выполняются коммутативный и ассоциативный законы, закон упорядочения и закон поглощения. Однако закон дистрибутивности в квантовой логике, в общем случае, не выполняется.

Чтобы убедится в этом, рассмотрим три вектора A, B , C в двумерном евклидовом пространстве (рис. 12) и высказывания А, В и С , состоящие в том, что вектор у направлен вдоль соответствующего вектора.

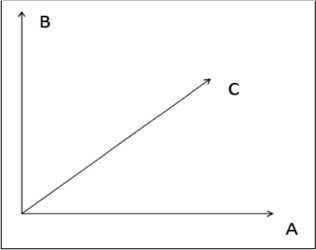
Рис. 12. Векторы A , B , C в двумерном евклидовом пространстве

Имеем A + B = I , ( A + B = I ) C = C . С другой стороны, AC = 6 , BC = 6 , где 6 - абсурдное высказывание. Поэтому AC + BC = 6 . Таким образом, дистрибутивный закон не выполняется: ( A + B ) C ^ AC + BC . Нарушение дистрибутивности составляет основное отличие квантовой логики. Наличие данной особенности отличает квантовую логику от Аристотелевой логики [5,26].

Основным объектом квантовой логики являются решетки. Допустим, что состояния некоторой системы описываются решеткой (рис. 13).

На рис. 13 состояние 0 означает «никакое» или «ложное», состояния 1, 2, 3, 4 являются взаимоисключающими друг друга состояниями, так что состояние 1 и 2 (обозначение 1 л 2 ) есть 0; аналогично 1 л 3 = 1 л 4 = 2 л 3 = 0 . I - всегда реализующееся состояние I = 1 v 2 v 3 v 4 , где v - знак дизъюнкции, и 1 v 2 = 1 v 3 = 2 v 3 = 3 v 4 = I .

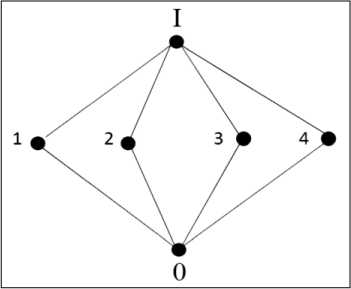
Рис. 13. Вид недистрибутивной решетки

Нетрудно заметить, что решетка на рис. 13 недистрибутивна

1 л ( 3 v 4 ) = 1 л I = 1 * ( 1 л 3 ) v ( 1 л 4 ) = 0 v 0 = 0 .

Другой важной особенностью данной решетки является невозможность определения на ней вероятностной меры [27]. Действительно, если все состояния равноправны, то естественно приписать любому из состояний 1, 2, 3, 4 вероятность % , но тогда вероятность состояния 1 v 2 по теореме сложения вероятностей есть % , однако 1 v 2 = I , и, следовательно, эта вероятность равна 1. Поэтому в квантовой механике поведение динамической системы описывается не вероятностью, а амплитудой вероятности, которая, в свою очередь, позволяет вычислять условные вероятности.

Рассмотрим теперь особенность логики квантовых операций на примерах классических логических операций, содержащих или состоящих из внутренних квантовых операций [28].

Пример 1: Операция корень квадратный из операции «отрицание» . Рассмотрим понятие кванто-

0 )

1 у

вый бит (кубит) | ^ ) = (10) = f

= —=(|0)±|1) ) , который играет важную роль в квантовой 2

теории информации. Кубит является квантовой суперпозицией двух классических состояний в виде логического базиса (| 0) ,| 1)) . Логическая операция «НЕТ», действуя на кубит | ^ ) , является линейным оператором not : С² ^ С² , который действует на все логические базисы следующим образом: not|0) = 11), not 11^ = |0) . Соответствующее матричное представление в логическом базисе имеет вид:

0   1 )

и является т.н. матрицей Паули ст .

10 )                         *

Рассмотрим теперь нелинейную операцию not над операцией not. Результат операции not является линейным оператором Vnot :С2 ^ С2, который, действуя на кубит над всеми логическими базисами, приводит к следующему результату:

Г 0  1 )

I 1  0 J

Г 1 + i

1 — i

I 2

• 1    — i '

• 2   , Vnotlo) = 1 + i |0 + 1— i |1>; Vnotl¹) = 1— i |⁰) + 1 + i .

• 1    + i                2        2                   2        2

• 2    J

Физически данный результат означает, что измерение выходного результата (|0),|1)) , если входом является сигнал 0 , дает:

0 , с вероятностью

1 , с вероятностью

.

Аналогично для входа 1 .

Таким образом, оператор not является случайным переключателем. Интуитивно такой переключатель должен сохранять данное свойство, если его применить дважды. Однако это свойство не выполняется и применение дважды оператора V not Vnot = not, т.е., V notVnot | ^ } = not | ^ ). Объясняется данный «парадоксальный» факт тем, что в квантовой механике при оценке эволюции вероятности квантовых переходов осуществляется по законам сложения амплитуд вероятностей по всем возможным путям траекторий движения, а не самих вероятностей. Амплитуда вероятностей может быть уменьшена (деструктивная интерференция) или усилена (конструктивная интерференция) в процессе суммирования амплитуд вероятностей, что существенно отличает квантовые операции от классических вероятностных операций. Операцию not часто именуют как «возможное (“tentative”)» отрицание или «полу-отрицание (half-negation)»: применение дважды оператора not приводит к полному классическому логическому отрицанию not . Отметим, что применение оператора not к вычислительному базису (| о) ,| 1) ) приводит к формированию квантовой суперпозиции с комплексными амплитудами вероятности. Поэтому нелинейный оператор not является сугубо квантовым оператором, не имеющим аналогов в классической и нечеткой логике.

Таким образом, операция классического логического отрицания состоит из двух внутренних квантовых операторов, реализующих конструктивную и деструктивную интерференцию амплитуд вероятностей.

Пример 2: Корень квадратный из оператора идентичности . Для заданного n ^ 1 корень квадратный из оператора идентичности на пространстве ® n С² (® ⁿ - знак тензорного умножения) является линейным оператором V I ⁽ n ) таким, что для любого элемента | x j,..., x^) в вычислительном базисе 13 ^{( n} ) выполняется следующее условие:

⁽l \,-, ' ^ = l x ,,-', x —1) ® -/= ( ("0 xⁿ l x . ) ⁺ I¹ - X )) .

Основным свойством оператора

^I ^{( n} ) ( V I ^{( n} ) | ^ )) = | ^ ). Очевидно, что

I ⁽ n ) является следующее: для каждого | ^ ) £® n С² ,

H , если n = 1

Т ( n — 1 )

I , остальное

1 Г 1       ¹

h =

V 2 V 1   — 1

.

Г  Г 1о)

Таким образом, операция ni = ₄ I     I порождает квантовый оператор Адамара, применение

\ V0  1J которого, например, к состоянию   |х1) = |0^, порождает квантовую суперпозицию

H 10) = —7= ( 0) +11)) с действительными значениями амплитуд вероятности. Следовательно, оператор

( n )                                                     ( n )

I , как и в случае not , может интерпретироваться как «возможное частное утверждение

(tentative partial assertion)», преобразующее точную определенную информацию в максимально неопределенную информацию [27, 28]. Очевидно, что применение оператора 41n ) приводит состояние системы к максимальному беспорядку. Применение этого оператора дважды возвращает систему в исходное состояние с сохранением начальной информации об исходном состоянии.

Приведенные примеры указывают на существование «скрытой» квантовой информации в классических состояниях, извлечение которой дает дополнительные возможности для формирования эффективных квантовых стратегий на пространстве классических стратегий принятия решений.

8.    Роль выбора моделей квантовых алгоритмов в задачах интеллектуального робастного управления

Квантовые вычисления и алгоритмы, в отличие от классических аналогов, в первую очередь позволяют непосредственно определить качественные свойства исследуемой функции, кодируя их в начальных квантовых состояниях суперпозиции. Для поиска решения с помощью квантовых алгоритмов (КА) целенаправленно изменяют исходную суперпозицию начальных состояний, в которой закодировано искомое решение, применяя последовательно соответствующие типы квантовых операторов. В этом случае может быть использован алгебраический формализм. Применяемый алгебраический формализм поддерживается абстрагированием логического вывода относительно квантовых эффектов и отображает важнейшие квантовые эффекты программным путем, устраняя трудность аппаратной реализации, такую как декогерентность. Поэтому в квантовых вычислениях и моделях КА особую роль играет выбор модели вантовых операторов.

Отметим, что если операторы ГА описаны, достаточно хорошо известны и имеют четкую физическую интерпретацию по аналогии с биологическими механизмами эволюции естественного отбора Дарвина, то операторы КА менее известны в инженерных приложениях и требуют более детального рассмотрения физической интерпретации и математической формализации квантовых вычислений.

На рис. 14 приведено сравнение операторов ГА и КА.

Минимум производства энтропии

Метод решения

Функция пригодности

Классический подход

оптимизация

Основная проблема

Глобальная

алгоритмы

Структуры Квантовые поисковые

Квантовый

ГА подход

Суперпозиция решений Квантовые операции

0 1  0 .…0 1  1  0

Моделирование суперпозиции

Квантовые операторы и измерения оракула т

Изменение вероятности выбора

Скрещивание

Операторы ГА

Начальное состояние (0,1)

Селекция ( Репродукция )

Мутация

Двух битовая

ЯЧРЙКЯ ( .1,(1

Двоичное кодирование

Исходное состояние

Экспертное решение

Пространство

-^ Решений N (п)

уперпозиция

^(10) ±11)

Классические состояния т3

Обобщенное пространство решений

Пространство

D Решений 1 , 2

Запутанные состояния

Некоррелированные состояния

Суперпозиция

Моделирование запутанных состояний

Пространство

GA operations

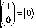
₁    решений

2       ⁿ      Пространства решений

Рис. 14. Сравнение структур ГА и КА (КПФ – квантовое преобразование Фурье)

Рассмотрим кратко некоторые особенности квантовых операторов, составляющих основу КА, а также физическую интерпретацию результата действия от применения квантовых операторов.

• 8.1.    Структура квантовых вычислений и КА

В теории квантовых вычислений можно выделить два направления исследований:

• •    задано множество точек функционала S = { ( x , у ) } , необходимо найти вид такого оператора U , чтобы выполнялось условие у = U • x ;

• •    задана проблема (КА), необходимо найти вид квантовой схемы - квантовой алгоритмической ячейки (КАЯ), решающей заданную проблему (реализующей данный КА).

Алгоритмы решения данных задач могут быть реализованы как на аппаратных средствах в виде КАЯ, так и на программном уровне с помощью соответствующего программного инструментария (toolkit) квантового программирования и с реализацией на классическом компьютере в среде МАТ-ЛАБ. Возможность [18] эффективного моделирования КА на классическом компьютере используется в Части 2 для моделирования КА.

Фундаментальный результат теории квантовых вычислений заключается в том, что все операции (подобно классическому случаю) могут быть реализованы схемой, состоящей из универсальных базисных элементов. Однако, в отличии от классического аналога, КАЯ могут быть выполнены на различных классах универсальных элементов в зависимости от используемого вычислительного базиса. КАЯ (с фиксированными вычислительными и измерительными базисами) обеспечивают описание эволюции некоторого унитарного оператора U , которому соответствует квантовый вычислительный процесс:

IV= U к),

где вектор (волновая функция) к / задает начальные условия вычислений (решаемой проблемы), а |^V отражает результат вычислений за счёт действия оператора U на начальное состояние к )•

Примечание . Кет-вектор ψ в обозначениях Дирака представляет n -мерный вектор-столбец.

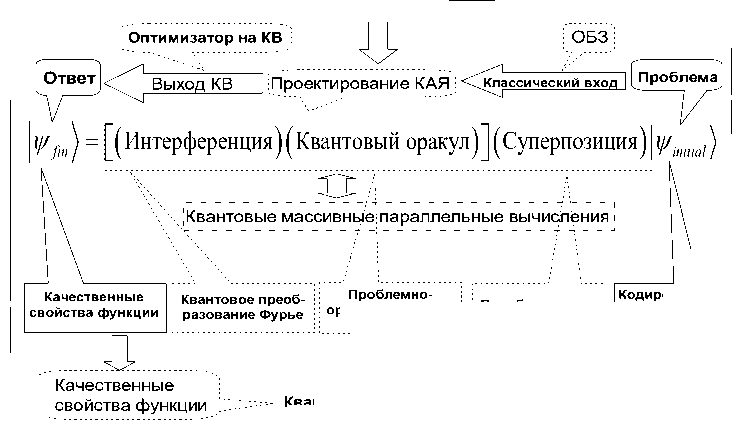
На рис. 15 показана типовая структура КА.

Основа применения квантовых вычислений

ОБЗ

Оптимизатор на КВ

Проблема

Проектирование КАЯ

Выход КВ

Классический вход

Квантовые массивные параллельные вычисления

Проблемно

Качественные свойства функции

Квантовое преоб- разование Фурье ориентированный

Качественные свойства функции

Кодирование свойств функции

Преобразование Адамара оператор

Квантовый оракул в виде черного ящика

Рис. 15. Обобщенная структура КА

Выбирая различный вид оператора ^U (в частности, Гамильтониан), можно сформировать различные модели квантовых вычислений.

В общем виде модель квантовых вычислений состоит из пяти этапов:

• -    приготовление начального (классического или квантового) состояния | ^_т ) ;

• -  выполнение преобразования Адамара H для начального состояния с целью подготовки со

стояния суперпозиции;

• -  применение оператора запутанных состояний или оператора квантовой корреляции (кванто

вого оракула) к суперпозиционному состоянию;

• -    применение оператора интерференции;

• -    использование оператора измерения для результата квантовых вычислений | v_fm ) .

Таким образом, система моделирования квантовых вычислений и КА реализуется на классических компьютерах с применением КАЯ. Процесс проектирования КАЯ в матричной форме заключается в проектировании трех квантовых операторов: суперпозиции ( Sup ), квантовой корреляции (запутанных состояний – entanglement U ), и интерференции ( Int ) и составляют основу структур КА.

В общем виде структура КАЯ может быть представлена в виде

КАЯ = [ ( Int 0 ⁿ I ) • U_F ] h + 1 • [ ⁿ H 0 m S ] ,

где I - оператор идентичности; ® - символ тензорного произведения; S равен I или матрице Адамара и выбор зависит от описания исследуемых свойств функции.

Одной из особенностей процесса проектирования (10) является выбор типа оператора U , физически описывающий тип квантовой корреляции и закодированные в суперпозиции качественные свойства исследуемой функции f .

Работа квантовых операторов осуществляется в итеративном режиме в зависимости от типа КА. При этом для общего случая предполагается, что определённые вычислительные проблемы могут быть решены на квантовом компьютере более эффективно (с меньшей вычислительной сложностью, так называемая NP - проблема), чем на классическом компьютере. Более того, с помощью эффективного применения квантового компьютера достигаются решения алгоритмически не разрешимых (на классическом уровне) проблем.

Таким образом, существуют эффективно решаемые с помощью применения КА задачи, для которых не существует ни одного успешного классического (рандомизированного) алгоритма.

Эти наблюдения свидетельствуют о том, что КА составляют физически обоснованный базис не только техники ускорения вычислений, но и поиска решений сложных проблем, используя такие квантовые законы, как суперпозиция (для расширения пространства возможных решений), квантовый параллелизм процессов вычислений (в интересах ускорения поиска решений) и квантовая интерференция (с целью извлечения искомого решения).

Так, например, тензорное произведение является обобщением билинейной операции произведе-

i a ния матриц: A ® I

V c

b

d у

A х a  A x b

A x c  A x d _v

имеет следующие свойства:

( a ) Ранг ( A ® B ) = Ранг ( A ) + Ранг ( B ) ;

( b ) Размерность ( A ® B ) = Размерность ( A ) x Размерность ( B )

Таким образом, с помощью тензорного произведения можно экспоненциально расширить рабочее пространство вычислений и сформировать базис для параллельных вычислений . В этом смысле суперпозиция выступает как первый этап на пути организации квантового параллелизма.

Дополнительно к отмеченным вычислительным ресурсам, квантовая корреляция рассматривается как новый физический вычислительный ресурс, позволяющий резко увеличить успешный поиск решений проблем ранее не рассматриваемых в классической области вычислений. К таким проблемам относятся: телепортация, сверхплотное кодирование, передача данных по квантовым каналам

Сетевое научное издание «Системный анализ в науке и образовании» Выпуск № 3, 2022 год связи с повышенным уровнем секретности и защиты (от несанкционированного доступа или подслушивания), коррекция квантовых кодов с заданным уровнем толерантности и др.

Квантовые алгоритмы (КА) основаны на физических законах теории квантовых вычислений, а именно в вычислениях участвуют унитарные, обратимые квантовые операторы. В общем виде КА, согласно рис. 15, состоит из трёх основных унитарных операций: суперпозиция; квантовая корреляция (квантовый оракул или запутанные операторы) и интерференция. Четвёртый оператор, оператор измерения результатов квантовых вычислений, является необратимым (классическим). Квантовые вычисления, основанные на перечисленных типах операторов, относятся к новому виду интеллектуальных вычислений.

• 8.2.    КА в задачах интеллектуального робастного управления

Одним из основных назначений и преимуществ эффективного применения ИСУ является возможность гарантированного достижения цели управления с максимальным качеством управления на верхнем уровне и минимальным расходом полезного ресурса системы « объект управления (ОУ) + регулятор » на нижнем (исполнительском) уровне иерархической системы автоматического управления (САУ).

На содержательном уровне данная возможность отражает назначение целенаправленной деятельности ИСУ в общем случае непредвиденных ситуаций управления. При этом эффективность применения ИСУ зависит от уровня интеллектуальности разработанной системы.

Важную роль при формировании уровня интеллектуальности САУ играет выбор используемого инструментария технологии интеллектуальных вычислений для проектирования соответствующей БЗ при заданной цели управления.

Положительные результаты применения классических технологий интеллектуальных вычислений (типа мягких вычислений) совместно с аппаратом квантовых вычислений привело к новому альтернативному подходу – применению технологии квантовых интеллектуальных вычислений в задачах оптимизации процессов управления классическими ОУ (физический аналог применения обратного метода исследования « квантовая система управления – классический ОУ »). Такой подход также существенно расширяет возможности самих интеллектуальных вычислений.

Рассмотрим классификацию КА. С точки зрения функциональных возможностей КА классифицируются на две группы: алгоритмы принятия решений и поисковые алгоритмы.

Классификация КА и их применение в задачах управления отражены рис. 16.

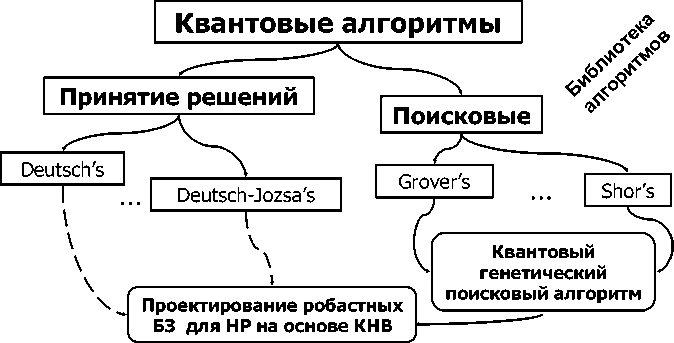
Рис. 16. Классификация КА

Аналогии между мягкими и квантовыми вычислениями приведены на рис. 17.

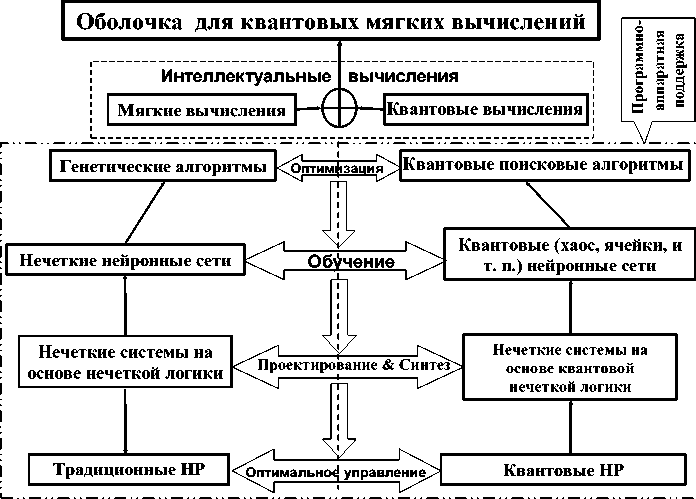
Рис. 17. Аналоги мягких и квантовых вычислений

Особенности эффекта существования «скрытой» квантовой информации в классических состояниях, извлечение которой дает дополнительные ресурсы для формирования эффективных интеллектуальных процессов управления в условиях риска и непредвиденных ситуаций управления за счет квантовой корреляции, включаются в структуру информационной технологии проектирования робастных самоорганизующихся ИСУ.

Физическая интерпретация данных особенностей и механизма извлечения скрытой квантовой информации подробно описаны в Части 2.

Выводы

Рассмотрены вопросы физической строгости и математической корректности интерпретации адекватности математической модели рассматриваемой физической модели конечного объекта управления.

Приведены оценки вычислительной и информационной сложности моделей конечного объекта и рассмотрены взаимосвязи соответствующих мер сложности.

Приведено описание особенностей процессов ИТ-образования при подготовке специалистов нового поколения квантовых сквозных ИТ для проектирования интеллектуальных систем управления.

Обсуждаются логические «парадоксы» технологии интеллектуальных вычислений, возникающие при применении указанных технологий в процессах ИТ - образования.