балансироваться на низких частотах с использованием только двух плоскостей коррекции.

Наибольшая сложность при балансировке гибких роторов связана с потребностью в высокочастотных балансировочных стендах, оснащенных вакуумными камерами, современной виброизмерительной аппаратурой и вычислительной техникой. Только в этом случае могут быть замерены динамические реакции или прогибы, определены балансировочные коэффициенты и выполнены соответствующие условия балансировки. Эффективность же известных способов низкочастотной балансировки носит статистический характер и не может служить гарантией надежной безвибрационной работы каждого отдельного изделия. Важное исключение составляют роторы, распределение дисбалансов которых может быть найдено по результатам измерений на низкочастотных балансировочных станках. К ним, в частности, относятся роторы, выполненные в виде центрального вала, несущего на себе ряд дисков (рис. 1).

Соответствующая технология включает следующие операции:          _{r r}

• 1.    Измерение дисбалансов A_o и B_o , центрального вала в плоскостях опорных подшипников.

• 2.    Сборка первого промежуточного узла, который состоит из вала и одного из дисков, _r и изм _r е-рение в тех же плоскостях дисбалансов A ₁ и B ₁ .

• 3.    Операция 2 последовательно повторяется для второго узла, который состоит из двух дисков, затем для третьего, четвертого, и, наконец, последнего N -го узла, представляющего уже окончательно собранный ротор.             _r

_r 4. По результатам измерения дисбалансов A_k и B_k ( k =0… N ) последовательно определяются:

• а)    проекции дисбалансов А_ky , А _kz и B_ky , B _kz на координатные плоскости YX и ZX , жестко связанные с ротором (ось Х направлена по оси вращения);

• б)    проекции статических U_ky , U_kz и моментных V_ky , V_kz дисбалансов самих дисков:

  

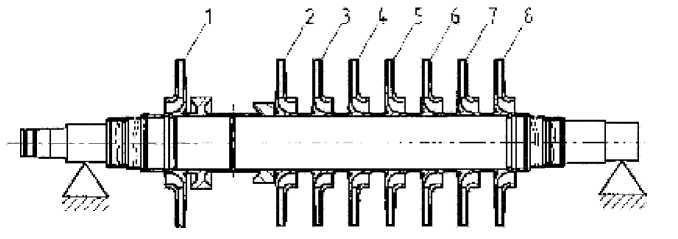
  Рис. 1. Ротор центробежного компрессора системы агрегатов “Синтезгаз”

  
  

  U ky - A A ky + A B ky ; U kz - A A kz + A B kz , (2)

  V - A A ky X k -A B ky (l - X k ); V y - A A kz X k -A B^l - x_k) , (3) где A A ky - A ky - A k — 1, y ; A B ky - B ky - B k — 1, y ; A A kz - A kz - A k - 1, z ; A B kz - B kz - B k - 1, z ; k - номер балансируемого узла; x_k – расстояние от левой опоры до центра масс k -го диска. Таким образом, функция распределения дисбалансов становится полностью определенной.

  Далее, в соответствии с принятыми условиями уравновешивания рассчитываются дисбалансы корректирующих масс. Приведем необходимые для этого формулы и уравнения, имея в виду следующие два метода балансировки:

  А. Балансировка по собственным формам колебаний в 4-х плоскостях коррекции:

  
  

  где а _рi , а _qi – коэффициенты динамической податливости, найденные для максимальной угло- ( 0 )      ( 0 )

  вой скорости вращения; r_pz , r_qz – проекции динамического прогиба, возбуждаемого началь-

  
  

  ным дисбалансом.

  
  

  Для определения динамических коэффици-

  
  

  ентов а _рi , а_qi решается следующая система уравнений:

  
  

  h_ki = ®¹

  
  

  Z mjhj^akj + Sa_ki k,

  
  
  
  

  [ Z D iz -- Z U kz ; ⁱ                     k

  Z D „ x, .- J^ + V , )•

  ' Z D.n , ( x , ) -- K (4)

  Z ^Dizn 2 ^{( X}i) ^{= - K} 2 z , ^ i

  где

  ^K 1 z ^-Zk n ^{( x}k ^{) +} V ky H i ^{( x}k ^)] ; k

  ^K 2 z ^- Z V^u k A2i ^{( x}k ^{) +} V ky n 2 ^{( x}k ^)] ; k

  П 1 ( x_k ) , П ₂ ( x_k ) — собственные формы колебаний ротора; K 1 z , K ₂ z - составляющие начального дисбаланса по указанным собственным формам.

  В. Балансировка с устранением прогибов в заданных точках p и q ротора:

  
  

  k,j' - 1 ...N, i - 1 ... 4 ,

  где S_i – единичный дисбаланс в одной из плоскостей коррекции; a _ki , a _k j - статические коэффициенты податливости. Искомые динамические коэффициенты будут при этом равны:

  а рi = h рi ; а qi = h qi . (7)

  Прогибы, определяемые начальным дисбалансом, будут найдены по результатам решения другой системы уравнений:

  
  

  _ r - ⁰ ) - _Ю ²

  
  

  Z ( ^mj r j ° e ^{+ u}> an ⁺ V jy P k^ • (8)

  
  

  j,k - 1 ...N,

  где a _k j , P _k j - статические коэффициенты податливости.

  
  

  Уравнения, аналогичные (4), (5), (8), записы ваются и для плоскости YX , после чего определя

  
  

  _-

  
  

  _-

  
  

  ются проекции корректирующих дисбалансов D_iy , а также модули и углы этих дисбалансов:

  ^D, ^- V ^Di ⁺ D iz ; a ^- arccos DDy ^.    (9)

  С. Балансировка в 3-х плоскостях к ⁱ оррекции с устранением прогиба в одной точке (точке p ):

  
  

  Z D iz -- Z U kz ik

  
  

  У D,x, - -У (u_tzx_t iz i                  kz k

  ik

  у D a =-r^{( 0} ); iz рi         pz

  i

  
  

  + V ky >-

  
  
  
  

  Z D ,z a q,-- г ( ⁰ ’ ■

  
  

  i

  
  

  ' 3

  Z D z -- Z U kz ;

  i ^{- 1}                  k

  \ Z ^D « X i --Z< ^U» x . + V ky )

  i - ^{1                     k}

  у D a =-r ⁽⁰⁾, / J Iz р I ^>z s

  . i - 1

  
  

Эффективность балансировки можно оценить коэффициентами:

γ _k = r_k/r k 0 ,               (10)

где r_k , r_{k 0} – динамические прогибы в точках x = x_k отбалансированного и неотбалансиро-ванного ротора.

При определении rk используются уравнения (8), в правые части которых включаются суммы: ∑ D izαki – при определении проекций r iz или ∑ D iyαki – при определении проекций rky .

Очевидна зависимость качества балансировки от множества факторов: распределения началь- ного дисбаланса, характера выдвигаемых динамических условий, положения плоскостей коррекции и т.д. Отсюда вытекает необходимость в оптимизации этого процесса с целью достижения минимальных значений коэффициентов γk и, что не менее важно, минимальных значений корректирующих дисбалансов. Быстродействие современных ПК позволяет решать эту задачу для каждого конкретного ротора непосредственно в производственных условиях.

Некоторые результаты такого расчета, выполненного для ротора компрессора высокого давления агрегата “Синтезгаз” (производство аммиака), представлены на рис. 2, 3, 4. Здесь ν =1…12 обозначают различные сочетания усло-

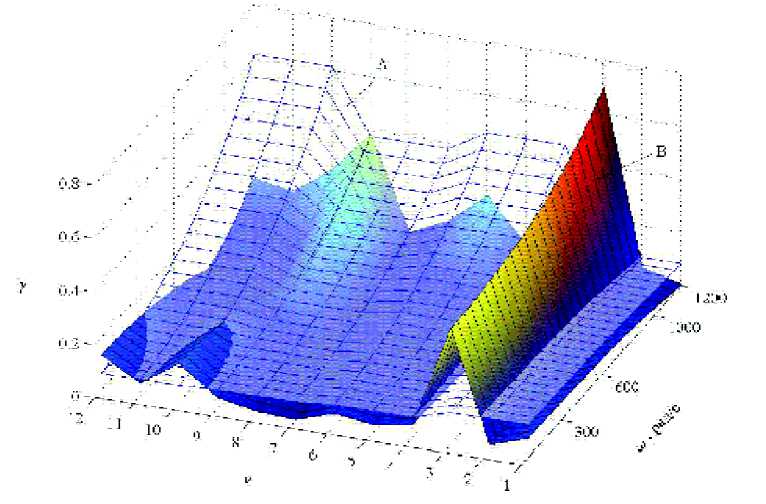
Рис. 2. Графики γ ( ν ), при ω =0…1200 рад/с

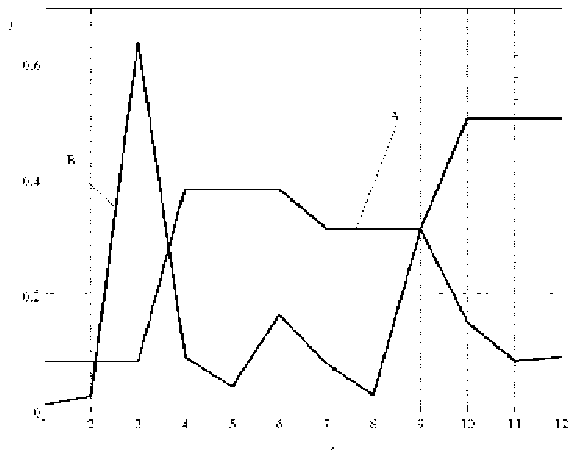
Рис. 3. Графики γ ( ν ), ω =1100 рад/с

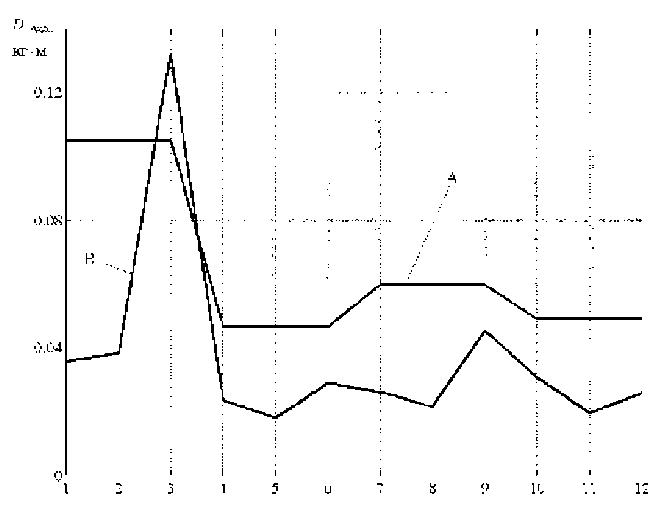
Рис. 4. Графики D max ( v ), а =1100 рад/с

вий, по которым определялись дисбалансы корректирующих масс (табл. 1). Результаты расчета приведены для центральной точки x = x 5 .

Довольно неожиданно возникла еще одна трудность – чрезмерно большие значения корректирующих масс, на один…два порядка превышающие уровень начальных дисбалансов. Данная ситуация была вызвана чрезмерно малой обусловленностью матриц, соответствующих системам уравнений (1)…(3).

Для решения этих проблем была разработана программа, работающая в среде MATLAB 6.1, которая позволяет рассматривать большое число вариантов балансировки, отличающихся друг от друга характером динамических условий, налагаемых на корректирующие массы, числом и расположением плоскостей коррекции, положением точек устранения прогиба, а также угловой скоростью балансировки. Быстродействие современных пер- сональных компьютеров позволяет решать эту задачу для каждого конкретного ротора и непосредственно в производственных условиях.

Некоторые результаты такого расчета, выполненного для ротора компрессора высокого давления агрегата “Синтезгаз” (производство аммиака), представлены на рис. 5, 6. Здесь v =1^12 обозначают различные сочетания условий, по которым определялись дисбалансы корректирующих масс (см. табл. 2). Результаты расчета приведены для центральной точки x = x 5 .

Полученные результаты позволяют уверенно выбрать оптимальное сочетание параметров балансировки, при котором достигается минимальные трудоемкость коррекции и уровень вибрации, возбуждаемой начальным дисбалансом.

Использование результатов расчета в производстве играет существенную роль, особенно в тех случаях, когда коррекция дисбаланса дос-

Таблица 1. Сочетания условий для определения дисбалансов корректирующих масс

V	1	2	з	4	5	6	7	8	9	10	П	12
Метод балансировки	А, В
Плоскости коррекции	1 4 7 8	1 4 7 8	1 2 6 8	1 2 6 8	1 2 6 8	1 3 6 8	1 3 6 8	1 3 6 8	1 2 5 8	1 2 5 8	1 2 5 8	1 4 7 8
Точки устранения прогибов	4 7	3 6	4 7	3 6	1 4	4 7	3 6	1 4	4 7	3 6	1 4	1 4
Метод балансировки	С
Плоскости коррекции	1 4 8	1 4 8	1 3 8	1 3 8	1 5 8	1 5 8	1 2 8	1 2 8	1 4 8	1 3 8	1 5 8	1 2 8
Точки устранения прогибов	4	5	3	4	5	3	4	5	3	4	5	3

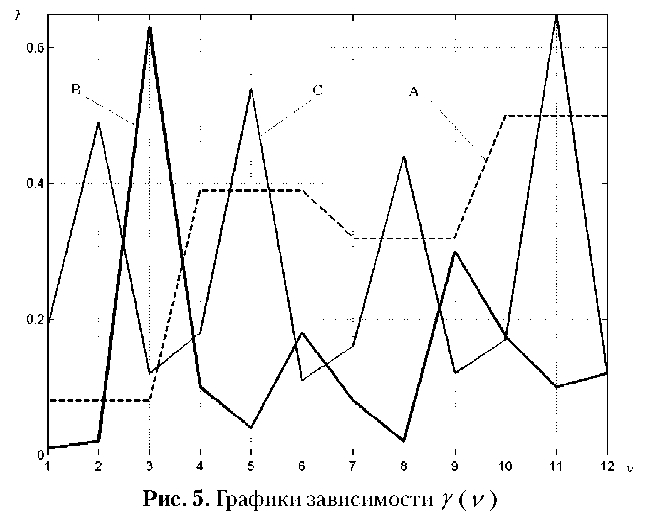
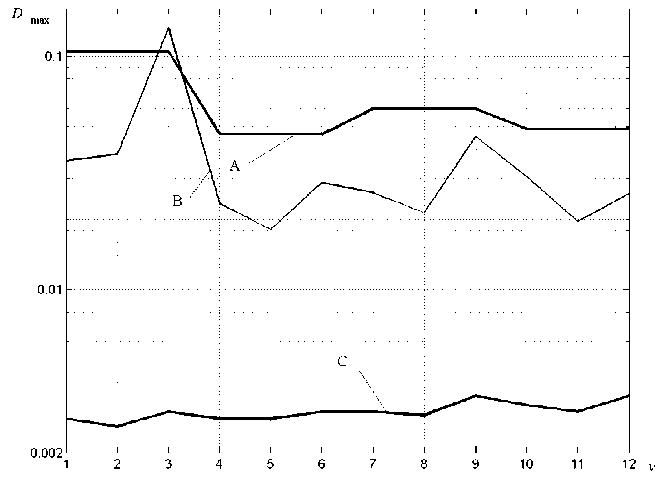
Рис. 6. Графики зависимости D _max ( ν )

Таблица 2. Сочетания условий для определения дисбалансов корректирующих масс

V 1 2 з 4 5 6 7 8 9 10 П 12 Метод балансировки А, В Плоскости коррекции 1 4 7 8 1 4 7 8 1 2 6 8 1 2 6 8 1 2 6 8 1 3 6 8 1 3 6 8 1 3 6 8 1 2 5 8 1 2 5 8 1 2 5 8 1 4 7 8 Точки устранения прогибов 4 7 3 6 4 7 3 6 1 4 4 7 3 6 1 4 4 7 3 6 1 4 1 4 Метод балансировки С Плоскости коррекции 1 4 8 1 4 8 1 3 8 1 3 8 1 5 8 1 5 8 1 2 8 1 2 8 1 4 8 1 3 8 1 5 8 1 2 8 Точки устранения прогибов 4 5 3 4 5 3 4 5 3 4 5 3 тигается за счет съема металла. Тогда необходимо обеспечить сочетаемость минимальных значений коэффициента γk с приемлемыми значениями дисбалансов корректирующих масс Di , поскольку резерв съема металла ограничен.