Технология моделирования нагружения несущих конструкций перерабатывающего оборудования с применением балочных элементов

Несущие конструкции являются одними из наиболее важных элементов оборудования различного назначения, в том числе перерабатывающего, поэтому точная оценка их напряженно-деформированного состояния в процессе эксплуатации определяет его надежность и безопасность.

Аналитические методы решения задач данного класса в настоящее время применяются достаточно редко, так как имеют более высокую трудоемкость и сложность по сравнению с численными методами. Последние получили широкое распространение с развитием технологий высокопроизводительных вычислений и соответствующего программного обеспечения (ANSYS, ABAQUS, LS-DYNA, NX CAE, ПК ЛИРА и др.). С учетом возможностей и популярности современных пакетов расчета, технологию моделирования несущих конструкций перерабатывающего оборудования целесообразно рассмотреть на примере расчета балочной несущей конструкции [1, с. 31] в системе конечно-элементного анализа ANSYS Mechanical APDL (MAPDL).

Расчетная схема нагружения рассматриваемой конструкции представлена на рисунке 1а. В ее рамках рассматривается нагружение двутавра немерной длины горячекатаного профиля 30Б2, выполненного из стали С345 категории 5 по ударной вязкости по ГОСТ 27772-2015 [2]: Двутавр НД – 30Б2 – ГК ГОСТ Р 57837-2017 /С345Б – 5 ГОСТ 27772-2015.

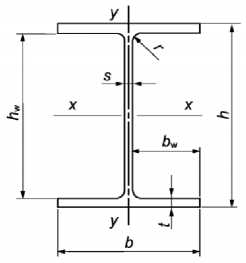
Параметры сечения двутавра приведены в таблице 1, а физико-механические характеристики материала, из которого он выполнен – в таблице 2.

В процессе нагружения двутавр опирается на две опоры, одна из которых неподвижная, а вторая – шарнирно-подвижная, допускающая перемещение двутавра вдоль его оси. К свободным концам двутавра приложена равномерно распределенная нагрузка w = 4000 Н/м.

Оценку напряженно-деформированного состояния несущей конструкции целесообразно выполнить на основе оценки максимальных изгибающих напряжений σ в средней части сечения балки и прогиба δ в ее центре.

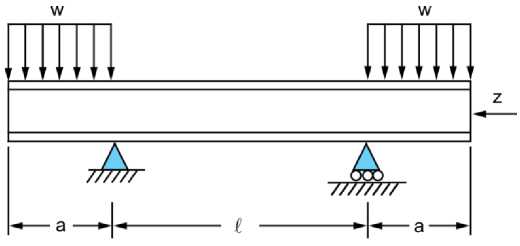
а)

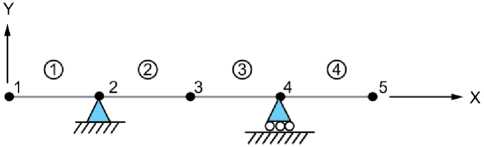
б)

Рис. 1. Расчетная схема (а) и конечно-элементная сетка (б) конструкции.

Таблица 1

Геометрические характеристики двутавра

•е о к & О о к	Номинальные размеры, мм							S о ^ ® ^ О g в 5 « 2 § к ® щ eg о	03 св .—1	Справочные величины для осей профиля
	h	b	s	t	h w	b w	r			I x , см4	W x , см3	S x , см3	i x , мм	I y , см4	W y , см3	S y , см3	i y , мм
30Б2	300	150	6,5	9,0	282	71,8	13	46,78	36,7	7209,3	480,6	271,1	124,1	507,5	67,7	52,6	32,9

Таблица 2

Основные физико-механические характеристики материала двутавра

Класс прочности	Толщина полки t , мм	Модуль Юнга E, Па	Предел текучести σ T , МПа	Временное сопротивление σ В , МПа	Относительное удлинение δ 5 , %
С345Б	9,0	2,1·1011	345	480	21

Моделирование нагружения балочных конструкций осуществляется с использованием графического интерфейса или командном (пакетном) режиме MAPDL в три этапа.

На первом этапе определяются свойства материалов, типы конечных элементов и их настройки, типы сечений балочных элементов и их параметры, задаются граничные (краевые) условия. Настройки параметров и запуск решения задачи осуществляется на втором этапе. На третьем этапе выводятся необходимые результаты решения. В случае, если прямое построение конечно-элементной модели имеет высокую трудоемкость, то как правило, сначала создается твердотельная модель конструкции, на которую затем наносится конечно-элементная сетка.

Для анализа балочных конструкций в MAPDL используются трехмерные линейные, квадратичные или кубические балочные элементы типа BEAM188 и BEAM189 (рисунок2), разработанные с учетом основных положений теории балок Тимошенко [3; 4] и допускающие искривление их поперечных сечений.

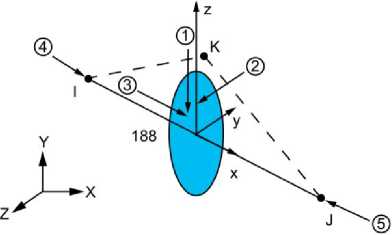
а)

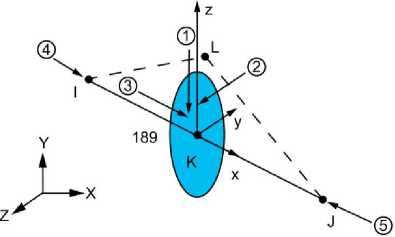
б)

Рис. 2. Геометрия элементов BEAM188 (а) и BEAM189 (б): I, J, K – узлы, X, Y, Z – оси.

Важно отметить, что ограничения теории деформации сдвига первого порядка позволяют адекватно описывать нагружение только тонких и умеренно толстых балок. Для оценки ее применимости используется коэффициент гибкости балочной конструкции :

к = GAL²/(EI z ) (1)

где G – модуль сдвига, Н/м²; А – площадь поперечного сечения, м²; L – длина сегмента балки, м; ( E I ) – изгибная жесткость, Н·м²; E – модуль упругости материала, Н/м²; I Z – главный момент инерции поперечного сечения балки относительно оси Z , м⁴.

Сравнение деформаций δ (таблица 3), полученных при нагружении консольнозакрепленной балки по схеме на рисунке 3, показывает, что с увеличением коэффициента гибкости адекватность результатов моделирования, полученных с использованием балочных элементов MAPDL,

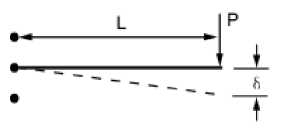
Рис. 3. Расчетная схема нагружения балки при оценке адекватности

моделирования.

нелинейно возрастает [5, с. 803]. С учетом этого ANSYS Inc. рекомендует [5, с. 803] использовать балочные элементы, когда значение коэффициента гибкости не менее 30.

Таблица 3

Влияние гибкости балки на адекватность результатов моделирования

№	Коэффициент гибкостиk	Соотношение деформаций, полученных с применением теорий Тимошенко δ T и Эйлера-Бернулли δ ЭБ k δ = δ T / δ ЭБ
1	25	1,120
2	50	1,060
3	100	1,030
4	1000	1,003

Кроме шести степеней свободы (перемещений и поворотов относительно X, Y и Z-осей) каждый узел балочных элементов может иметь седьмую степень свободы – деформацию.

Элементы BEAM188 и BEAM189 поддерживают модели упругости, пластичности, ползучести и другие нелинейные модели материалов, технологии рождения и смерти элементов, начальное состояние, большие отклонения и деформации, эффекты Кориолиса, нелинейную стабилизацию, самоупрочнение и другие.

В рамках рассматриваемой задачи создана конечно-элементная сетка, состоящая из 4 элементов типа BEAM188 и 5 узлов, как показано на рисунке 1б.Она построена таким образом, что в местах закрепления балки созданы узлы 2 и 4 , к которым применены соответствующие ограничения степеней свободы. Равномерно распределенная нагрузка w = 4000 кН/м приложена к балочным элементам 1 и 4 .

Тип сечения балок задается MAPDL-командой [6, c. 1453–1458]

SECTYPE,SECID,Type,Subtype,Name,REFINEKEY где SECID–идентификатор сечения; Type– тип сечения (для балок Type = BEAM); Subtype – тип формы сечения (рисунок 4); Name– имя сечения (не более 8 символов); REFINEKEY–уровень детализации сетки (0 – минимальная, 5 – максимальная).

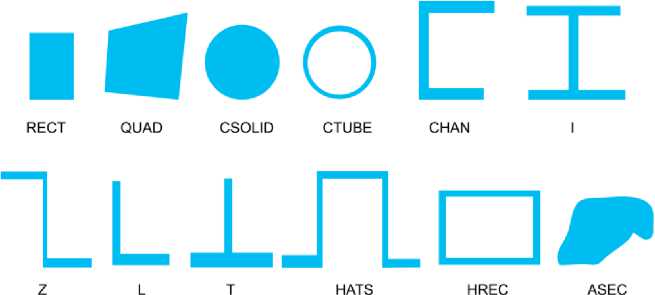
Рис. 4. Типы форм сечений балочных элементов MAPDL.

Применительно к рассматриваемой задаче в параметрах команды SECTYPE необходимо указать тип формы сечения (двутавр), задав Subtype = I .

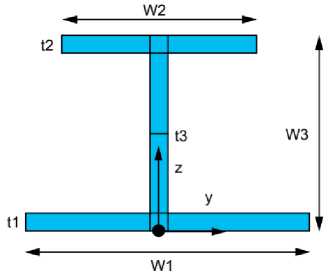
Рис. 5. Параметры двутавра.

В общем виде параметры формы сечения балки задаются командой

SECDATA VAL1, … VAL12

где VAL1 … VAL12 – значения параметров формы сечения [6, c. 1417-1439].

Применительно к сечению двутавра команда SECDATA должна быть записана в виде:

SECDATA W1 W2 W3 t1 t2 t3

где W1 W2 W3 t1 t2 и t3 – параметры двутавра (рисунок 5).

Ориентация Z и Y -осей сечения балочных элементов (рисунок 5) в MAPDL определяется положением узла K для элементов типа BEAM188 и узла L для BEAM189 (рисунок 2).

Ниже приведена последовательность команд для решения рассматриваемой задачи.

/PREP7 ANTYPE STATIC

! Вход в препроцессор PREP7 ! Тип анализа: статический

Задание свойств материала № 1

MP PRXY 0.3 MP EX 1 2.1e11

! Коэффициент Пуассона ! Модуль Юнга Ex = 2.1e11 Па

Выбор типа конечного элемента и его настройка

ET 1 BEAM188 KEYOPT 1 9 3 KEYOPT 1 3 3

! Тип элемента – BEAM188 ! Вывод данных: в 9 промежуточных точках ! Форма функции элемента вдоль оси: кубическая

Выбор типа сечения и настройка его параметров

Ih = 0.300 Ib = 0.150 It = 0.009 Is = 0.0065 SECT 1 BEAM I

! h = 0.3 м ! b = 0.15 м ! t = 0.009 м ! s = 0.0065 м ! Форма сечения №1: двутавр

SECDATA Ib Ib Ih It It Is     ! Задание размеров сечения швеллера

! Построение конечно-элементной сетки

N 1 N 5 4 N 6 0.5 0.1 N 10 3.5 0.1 FILL 1 5 FILL 6 10 E 1 2 6 EGEN 4 1 1 ! Задание граничных условий D 2 UX  UY D 4 UY NSEL S LOC Y 0 D ALL UZ D ALL ROTX D ALL ROTY NALL

! Создание узла № 1 с координатами (0;0;0) ! Создание узла № 5 с координатами (4;0;0) ! Создание узла ориентации № 6 с координатами (0.5;0.1;0) ! Создание узла ориентации № 10 с координатами (3.5;0.1;0) ! Генерирование узлов №№ 2-4 между узлами № 1 и № 5 ! Генерирование узлов ориентации между узлами № 6 и № 10 ! Создание элемента № 1 с узлами №№ 1, 2 и 6 ! Генерирование элементов №№ 2-4 по элементу-шаблону № 1 !    Запрет X Y-перемещений в узле № 2 !    Запрет Y-перемещений в узле № 4 !    Выбор узлов с Y = 0 !    Запрет Z-перемещений в выбранных узлах !    Запрет поворотов относительно оси X в выбранных узлах !    Запрет поворотов относительно оси Y в выбранных узлах !    Выбор всех узлов

Pw = 4000                ! Нагрузка w = 4000 Н/м

SFBEAM,1,1,PRES,Pw       ! Приложение нагрузки w к элементу 1

SFBEAM,4,1,PRES,Pw       ! Приложение нагрузки w к элементу 4

FINISH                   ! Выход из препроцессора PREP7

! Настройка и запуск решения

/SOLU                     ! Вход в процессор настройки решения Solution

OUTPR,BASIC,1 /OUT,SCRATCH

! Вывод результатов: основные величины, для каждого подшага

SOLVE                   ! Запуск решения

FINISH                  ! Выход из процессора SOLUTION

! Вывод результатов решения

/POST1                   ! Вход в постпроцессор POST1

SET,1,1                   ! Выбор результатов 1 подшага 1 шага решения

*GET,DISP,NODE,3,U,Y     ! ВыводY-перемещений в узле № 3

ETABLE,STRS,LS,1         ! Формирование таблицы напряжений в элементах

*GET,STRSS,ELEM,2,ETAB,STRS    ! Вывод напряжения в элементе № 2

FINISH                   ! Выход из постпроцессора POST1

Расчетная схема рассматриваемой задачи приведена на рисунке 6.

Рис. 6. Расчетная схема конструкции в MAPDL.

На рисунке 7 представлены исходное и деформированное состояния рассматриваемой балочной конструкции. Анализ полученных результатов решения показывает, что при заданной нагрузке максимальный прогиб в центральной части балки δ = 0,684 мм, а максимальное вертикальное перемещение ( U Y = 0,185 мм) наблюдалось на ее свободных концах. Максимальное напряжение в средней части сечения балки составило σ = 3,894 МПа, что значительно ниже соответствующих предельно допустимых значений.

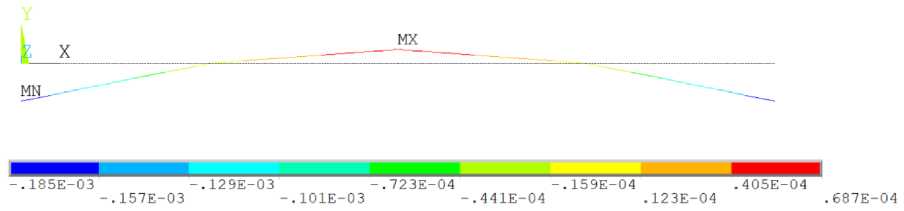
Рис. 7. Y-перемещения элементов конструкции.

Сравнение результатов аналитического расчета [7] и моделирования в MAPDL [1, с. 31], показывает, что погрешность не превышает 0,3%, поэтому балочные элементы типа BEAM188 могут эффективно использоваться для решения задач данного класса.

Настоящая работа является продолжением цикла работ [8–16], посвященных повышению эффективности применения современных технологий численного моделирования при разработке надежных и безопасных конструкций машин и оборудования АПК.