Технология нелинейного шифрования данных в высокоскоростных сетях связи

Широкое использование информационных систем в государственных учреждениях, финансовых структурах и военно-промышленном комплексе, а также быстрое развитие информационных систем общего пользования вызвало необходимость разработки средств защиты от несанкционированного доступа к информации и аутентификации пользователей [1-8]. Одним из критериев жизнеспособности современного государства является наличие защищенного, динамически развивающегося информационного пространства, пронизывающего все среды деятельности государства. На практике такое пространство складывается из информационных и автоматизированных систем управления, объединенных коммуникациями, и их создание становится задачей первостепенной важности.

Применение вычислительной техники в различных областях предопределяет необходимость разработки и создания адаптивных средств защиты информации в вычислительных сетях от несанкционированного доступа (НСД).

Основная часть

Защита информации представляет собой комплекс мероприятий, направленных на предотвращение несанкционированной утечки, модификации и удаления информации, осуществляемых с применением технических, в том числе и программных, средств [1-4]. Основной задачей обеспечения безопасности информационных компьютерных систем является защита информации и ограничение круга лиц, имеющих доступ к этой критичной информации.

При организации вычислительных сетей важная роль отводится защите сообщений, передаваемых по сети с использованием того или иного алгоритма шифрования. Анализ существующих систем защиты информации [1-8] показал, что все множество алгоритмов можно разбить на две основные группы. Основу первой группы составляют симметричные алгоритмы шифрования, работающие с секретным ключом. В данных системах защиты информации от НСД ключ расшифрования совпадает с ключом зашифрования.

Вторая группа включает в себя асимметричные алгоритмы шифрования, работающие с открытым ключом [1; 3; 5-6]. В таких алгоритмах для зашифрования и расшифрования используются разные ключи, причем знание одного из них не дает практической возможности определить другой. Асимметричные системы во многих случаях обеспечивают наилучшее решение проблемы распределения ключей. Однако следует отметить, что алгоритмы асимметричных систем защиты информации от НСД настолько трудоемки по сравнению с обычными алгоритмами симметричного шифрования, что на практике рационально их использовать там, где объем шифрованной информации незначителен. Поэтому, с помощью алгоритмов ассиметричных систем целесообразно распределять ключи и осуществлять аутентификацию пользователей путем использования электронной подписи, а с помощью симметричных алгоритмов осуществлять обмен большими шифровальными потоками [4-5; 8].

Современные системы поблочного шифрования потока данных используются до 32 раундов перемешивания и рассеивания символов для обеспечения высокой стойкости шифра и статической равномерности символов (битов) в шифрованном тексте. Применение в таких системах операций подстановок, перестановок и циклического сдвига позволяет использовать стандартные микропроцессоры и реализовать аппаратные средства с требуемым быстродействием. Однако в таких системах имеет место распространения ошибок на всю длину блока и обеспечивается низкая скорость шифрования при программной реализации из-за большого количества шифрующих операций [1-4].

С появлением новых средств мультимедиа и сетей с высокой пропускной способностью, обеспечивающих передачу мультимедийных данных большого объема, в современных вычислительных системах начинают применяться технологии, осуществляющие обработку и передачу больших массивов. Для обеспечения интерактивного обмена данными такие системы должны работать в реальном масштабе времени. Поэтому процедура обеспечения конфиденциальности и целостности информации должна реализоваться с использованием поточных алгоритмов зашифрования. Для реализации эффективных методов поточного шифрования данных требуется разработка псевдослучайных последовательностей (ПСП). Такие псевдослучайные последовательности могут быть получены в рамках теории конечного поля с использованием регистров сдвига на базе многократных фильтров [1-2; 4; 6]

Системы побитого шифрования потока данных обеспечивают высокое быстродействие процессов шифрования и дешифрования информации, как аппаратных, так и программных средств защиты информации. Несмотря на то, что шифр, основанный на сложении потока псевдослучайных битов с битами исходного текста по модулю два, в общем случае теоретически нераспознаваем, сама система шифрования не отличается стойкостью и может быть мгновенно раскрыта при наличии определенного количества символов исходного и шифрованного текста. Уязвимость системы к атакам на основе исходных и подобранных текстов обусловлено тем, что при битовом шифровании потока данных сложение символов по модулю два является единственным способом построения обратимой функции шифрования [6; 13].

Одним из наиболее перспективных способов защиты информации является применение систем поточного шифрования, использующие расширенные конечные поля GF(2v). Данные системы обладают более широкими возможностями по реализации различных криптографических функций обеспечения конфиденциальности и целостности информации. Применение различных операций, связанных со сложением, умножением, возведением в степень элементов конечного поля и их различных комбинаций позволяет реализовать адаптивные средства защиты информации, характеризующиеся высокой степенью информационной скрытности.

Нелинейное шифрование потока данных с операцией возведения в степень элемента конечного поля является одной из наиболее употребляемых криптографических процедур [1; 6-8]. Выбор данной процедуры обусловлен тем, что она нелинейна и для определения исходного текста по символам зашифрованного текста требуется вычисление дискретного логарифма [1; 3; 9-10]. Рассмотрим некоторые из них.

Как показано в [13] нелинейное шифрование потока данных можно реализовать с использованием операций сложения, умножения и возведения в степень элементов конечного поля, а также их комбинаций. При реализации нелинейного шифрования на основе операции сложения псевдослучайная последовательность элементов расширенного поля Галуа получается с помощью регистра сдвига, генерирующего двоичную ПСП. При этом двоичные числа снимаются одновременно с нескольких линий задержки на каждом такте работы регистра. Одновременно с регистра сдвига могут сниматься несколько псевдослучайных последовательностей элементов расширенного поля Галуа {x, y, …}. Данные символы могут сниматься с разных ячеек генератора двоичного ПСП и в разной последовательности, поэтому будут создавать различные последовательности символов расширенного поля Галуа, причем каждая из них не будет циклически сдвинутой относительно других псевдослучайных последовательностей элементов.

Тогда символы шифрованного текста определяются в результате решения уравнения

a(z) + yx1 (z) ^e(z)modn(z), (1) где х1 – целое число, которое выбирается заранее и используется постоянно или меняет- ся на каждом такте работы регистра сдвига; y(z) – полиномиальное представление псевдослучайной последовательности элементов поля Галуа; α(z) – символы исходного сообщения, представленные в полиномиальном виде; ord(α(z)) < ordπ(z) – степень полинома α(z); β(z) – полиномиальное представление шифрованного сообщения; π(z) – порождающий полином.

Дешифрование сообщений осуществляется путем решения уравнения

e(z) + (n(z) + y x ¹ (z)) mod n(z) = a(z) , (2)

где «+» – суммирование по модулю два.

В этом случае на приемной стороне вычисля-етсяпсевдослучайнаяпоследовательностьсимво-лов n (z) + y x ¹ (z) , сопряженная по отношению к псевдослучайной последовательности символов У x ^{1 (z) .}

При реализации нелинейного шифрования на основе операции умножения для шифрования символов исходного текста могут использоваться символы псевдослучайной последовательности конечного поля, возведенные в степень x . Аналогично, как и в предыдущем случае, x может быть постоянным числом или переменным, изменяемым по квазислучайному закону на каждом такте работы регистра сдвига или через определенное число тактов работы регистра сдвига. При этом зашифрованное сообщение определяется выражением

a(z)y(z) x ¹ =e(z)modn(z) .      (3)

Процедура дешифрования определяется следующим соотношением

^{e (}z)(y x ¹ (z)) ^{- 1} = ^a (z) mod ⁿ (z) ,

(4) где (y(z) х ¹ ) ^{- 1} mod n(z) - обратная величина функции y(z) x ¹ по модулю n(z).

В работе [13] показаны нелинейное шифрование потока данных с операцией возведения в степень символов конечного поля. В этом случае для шифрования поступающих на вход символов исходного текста, представленного в полиномиальной форме α(z)={αj(z)} вычисляются значениясимволовпсевдослучайной последовательности конечного поля х={xj} на различных текстах работы регистра сдвига j = 0; 1; 2 … и определяются символы шифрованного сообщения

a (z) ^x =e (z)mod n (z) .         (5)

Однако операция возведения элемента поля в степень трудоемка и требует больших затрат машинного времени. Для сокращения времени выполнения этой процедуры целесообразно перейти к обработке данных, представленных в полиномиальной системе классов вычетов (ПСКВ). Основные принципы построения этих непозиционных кодов, а также схемные реализации вычислительных устройств, функционирующих в ПСКВ, представлены в работах [11-12].

В этом случае поток входных битов разбивается на отдельные блоки. Каждый такой блок А двоичного кода представляется в полиномиальной форме А(z), причем степень данного полинома не должна превышать степень выбранного рабочего диапазона

n

P(z) = П p i ^(z) ,              (6)

i=1

то есть удовлетворять условию ordA(z) < ordP(z),           (7)

где p i (z) - неприводимый полином; i = 1; 2 .. n.

Тогда полином А(z), имея максимальную степень ordP(z) - 1, может быть представлен следующим образом:

ordP(z) - 1                  ordP(z) - 2

^A\z) = ¹ ordP(z) - 1 ^Z          + ¹ ordP(z) - 2 ^Z          +

1      0                  ⁽⁾

• • ••         1              0 Z-¹ ,

где l _k e {0;1... p -1}; k = 0;1 ... ordn(z) -1.

Исходя из условия построения системы криптографической защиты информации в расширенных полях Галуа на основе полиномиальной системы класса вычетов, имеем, что рабочий диапазон Р(z) представляет собой кольцо неприводимых полиномов p i (z), i = 1 ; 2 ... n , то есть определяется согласно выражению (6).

В этом случае, используя изоморфизм, порожденный китайской теоремой об остатках, а также учитывая условие (7), можно отметить, что каждый блок A(z), представленный в полиномиальной форме, однозначно представляется в виде набора остатков по выбранным основаниям P i ^(z)

A(z) = («1 (z),a2(z) ... an(z)).

При этом значение остатков будут заданы ordP(z)-1                  ordP(z)-2

ai (z) ( ordP(z)-1z         + ordP(z)-2z

... + l 1 z +1 0 )modp i (z);

где i = 1; 2 … n.

Для реализации алгоритма нелинейного шифрования с возведением в степень в расширенных полях Галуа GF(p ^v ) необходимо возвести j-ый блок А_j(z) в степень Х по модулю Р(z)

Χ j

P j (z) = А j (z)modP(z),        (11)

где j = 0; 1; 2; 3 …

Значение Х снимается с выходов линии задержки многотактового фильтра, генерирующего псевдослучайную последовательность. Структура многотактового фильтра будет определяться характеристическим многочленом p (z). Так как псевдослучайная последовательность может сниматься одновременно с выходов нескольких линий задержки, то желательно, чтобы степень порождающего полинома p (z) была значительно больше величины р ^v - 1 . Это позволит при определенных условиях нарушить детерминированные свойства ПСП. При этом последовательности Х, снимаемые с выходов разных линий задержки, не будут коррелированны друг с другом, что, в конечном итоге, позволит повысить степень криптографической защиты.

Двоичный поток псевдослучайной последовательности Х разбивается на блоки вида Х = {х₀; х₁; х₂…}, при этом каждый блок содержит не более чем р ^ν - 1 двоичных разряда. Данные блоки поступают на шифратор для реализации процедуры нелинейного шифрования согласно выражению (11). Так как блок A_j(z) представляется в виде набора остатков a i (z) , то справедливо следующее равенство

Χj в j (z) = А j (z)modP(z) =            (12)

= ((a1(z),a2(z)... aП(z))Xj modP(z), где aj (z) = Аj (z) mod pi (z).

Так как сравнения по одному и тому же модулю можно почленно умножать, то последнее выражение представляется в виде:

j xj                       j xj e j (z/ ((а1) (zA---Aa n ) (z))mu   \z)-V13)

Таким образом, операция возведения в степень по модулю Р(z), являющаяся основой разработанного алгоритма нелинейного шифрования, сводится к совокупности операций возведения в степень остатков a i (z) по соответствующим основаниям p i (z) .

На рис. 1 представлена структура нелинейного шифратора, функционирующего в полино- миальной системе классов вычетов. Исходный полином A(z) поступает на входы блоков, осуществляющих прямое преобразование из позиционного кода в ПСКВ (ПСС-ПСКВ). Полученные остатки aj (z), i = 1, 2... N, подаются на входы преобразователей «элемент-индекс» (Элеминд). С выходов данных преобразователей индексы в двоичном коде поступают на первые входы умножителей (Умн) по модулю рordpi (z) - 1 , где р – характеристика поля, ordp i (z) – степень i-го основания ПСКВ. На вторые входы поступает блок Xj, снимаемый с выхода генератора ПСП. Результаты произведения выдаются на входы преобразователей «индекс-элемент» (Инд-элем). На выходах этих преобразователей в двоичном коде получаются остатки зашифрованного сообщения, согласно (12).

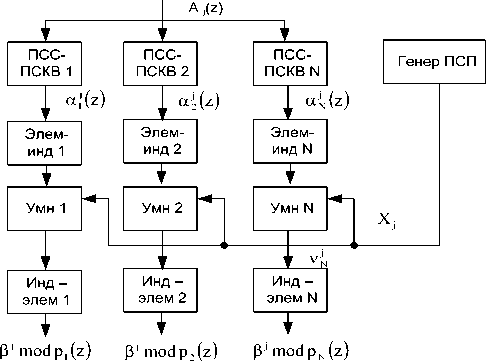
Рис. 1. Структура нелинейного шифратора, функционирующего в ПСКВ

Еслиi-ый остатокj-го блока отличен от нуля, то есть a j (z) ^ 0 , то он входит в состав мультипликативной группы, порождаемой неприводимым полиномом p i (z), взятым в состав оснований полиномиальной системы классов вычетов. Следовательно, при возведении в степень ненулевого элемента мультипликативной группы будет получен другой элемент этой группы, который является циклически сдвинутым на х_j разрядов влево.

В результате выполнения процедур нелинейного шифрования с использованием операции возведения в степень образуется кольцо, в котором будет отсутствовать делитель нуля. Таким образом, будет получена область целостности или целостное кольцо.

Если i-ый остаток j-го блока Aj(z) равен нулю, то при возведении в любую степень данный остаток будет равен также нулю.

Следует отметить, что если информацию о последовательности Х = {х0; х1; х2 …} снимать с выхода одной линии задержки многотактового фильтра, то может возникнуть ситуация, когда j-ый блок будет равен нулю. В этом случае целесообразно заменить нулевое значение блока хj на значение р ν - 2 . При этом такая замена должна осуществляться, соответственно, как на передающей стороне, так и на принимающей. Введение числа р ν - 2 вместо х = 0 позволит обеспечить j выполнение функции, обратной процедуре зашифрования, которая осуществлялась в шифраторе.

На приемной стороне осуществляется процедура расшифрования согласно

А j (z) = x j в j (z) modP(z).         (14)

Исходя из условия, что операции выполняются в кольце полинома Р(z), то справедливо aj (z) = xjpi (z) modpj (z),       (15)

где в i (z) = в j (z)modp i (z).

Очевидно, что применение параллельной обработки данных позволяет за счет выполнения мультипликативных операций с малоразрядными остатками повысить скорость зашифрования данных.

Рассмотрим процедуру расшифрования, выполняемую также с использованием полиномиальной системы. Как отмечалось ранее, для выполнения процедуры дешифрования используется выражение (15). Для вычисления корня степени х j из β j необходимо свести данную немодульную операцию к совокупности модульных. Исходя из условия

xj (xj)"1 = Imodpv -1,         (16)

необходимо определить мультипликативную обратную величину (x j ) ^{- 1} относительно x j по модулю p ^ν - 1. Для этого необходимо на приемной стороне использовать блок, позволяющий вычислить данную величину по значению x _j , поданному с выхода многотактового фильтра.

Рассмотрим пример реализации нелинейного шифрования в полиномиальной системе классов вычетов поле GF (23). В данном поле определены два неприводимых полинома третьей степени и один полином первой степени. Таким образом, данная система шифрования содержит следующие основания:

Pi (z) = z +1, p 2 (z) = z3 + z2 + 1, p 3 (z) = z3 + z + 1.

Произведение данных неприводимых полиномов образует рабочий диапазон, который

P(z) = П p i(z) = z 7 +11

i=1

Следовательно, для выполнения процедур нелинейного шифрования на основе возведения в степень по модулю с использованием ПСКВ необходимо поток битовой информации разбивать на блоки, содержащие по 7 бит каждый.

Пусть задана двоичная последовательность двоичных битов

Данная последовательность будет представлена в виде следующего набора блоков:

А1 = 0011110;

А2 = 1100011;

А3 = 0001111;

Представим эту последовательность блоков в полиномиальной форме. Получаем

A1 (z) = z4 + z3 + z2 + z ;

A2 (z) = z6 + z5 + z +1;

A 3 (z) = z3 + z2 + z +1.

Полученные значения поступают на входы модуля прямого преобразования двоичного позиционного кода в непозиционный код. Тогда блок А (z) в полиномиальной системе классов вычетов будет иметь вид

A1 (z) = z4 + z3 + z2 + z = (0, z2, z +1) .

Остальные блоки открытого текста представляются аналогичным образом:

A2 (z) = z6 + z5 + z +1 = (0, z2 + z, 1);

A3 (z) = z3 + z2 + z +1 = (0, z, z2) .

Чтобы повысить криптостойкость алгоритма нелинейного шифрования с использованием операции возведения в степень по модулю, предлагается снимать ПСП параллельно с выходов ν различных линий задержек генератора ПСП. Пусть двоичная последовательность двоичных разрядов в параллельном коде снимаемая с выходов трех линий задержек имеет вид

Х = {101, 110, 111, …}, что соответствует числам

Х5 = {5, 6, 7, …}.

Так как 7 = 0 mod 2³–1, то, как отмечалось ранее, это число меняем на p ^v - 2 = 2 3 - 2 = 6. В результате получаем последовательность

Х* = {5, 6, 6, …}.

Полученная последовательность Х* представляет собой показатели степеней, в которые необходимо возвести значение Аj(z), представленных в модулярном коде ПСКВ. Произведем криптографическое преобразование для блока А (z). Получаем

Р1 (z) = A5 (z) = (z4 + z3 + z2 + z)5 modz7 +1 = = z6 + z5 = 1100000.

Представим полученный результат в полиномиальной системе класса вычетов

a1 (z) = A5(z)modp1 (z) = |z6 + z5| 1 = 0 , a2(z) = А5(z)modp2(z) = |z6 + z51 3 2 1 = z2 +1,

a3 (z) = А5 (z)modp3(z) = |z6 + z5|     = z .

• ^{3             1                 3}                       z ³ + z + 1

Следовательно,

A5 (z) = z6 + z5 = (0,z2 + 1,z).

Выполним процедуру нелинейного шифрования в ПСКВ:

P1 (z) = A5 (z) = (z4 + z3 + z2 + z)5 modz7 +1 =

= (051+ |(z2)51+,       |(z +1) 51       ) = z+1           z3 +z2 +1             z3 +z+1

= (0, z2 +1, z).

Проведем криптографические преобразования с остальными блоками открытого текста. Для второго блока открытых данных получаем

в 2 (z) = A 6 (z) = |(z6 + z5 + z +1) 61 +, = z +1

=z6+z2 =1000100.

В полиномиальной системе класса вычетов данный результат получается в виде

p 2 (z) = A 2 (z) = z6 + z2 = (0,z,1) = (0,010,001).

Реализуем процедуру нелинейного шифрования в полиномиальной системе класса вычетов в2(z) = A6(z) = (z6 + z5 + z +1)6 modz7 +1 = = (|0 6|+ |(z2 + z) 6|+,      16|+,    ) = (0,z,1) = z+1                  z3 +z2 +1      z3 +z+1

= (0,010,001) .

Для третьего блока открытых данных вычислим значение зашифрованных данных:

в 3 (z) = A 3 (z) = |(z ³ + z ² + z + 1) 61 + 7 = z + 1

= z ⁴ + 1 = 0010001 .

Представим полученный результат в ПСКВ в 3 (z) = A 6 (z) = kz3 + z2 + z +1) 6| +7 = z +1

= z ⁴ + 1 = 0010001 .

Воспользуемся математическим аппаратом полиномиальной арифметики для выполнения процедур шифрования. Получаем

P3(z) = A6(z) = (z3 + z2 + z +1)6 modz7 +1 = = (0 6| + dz 6| +„ l(z2) 6| +    ) = z+1        z3z2 +1             z3 +z+1

= (0,z ² + z, z ² + z + 1) = (0,110,111) .

Полученный результат свидетельствует о возможности применения полиномиальной системы класса вычетов при реализации алгоритма нелинейного шифрования с использованием операции возведения в степень по модулю.

Очевидно, что применение параллельной обработки данных позволяет за счет выполнения мультипликативных операций с малоразрядными остатками повысить скорость зашифрования данных.

Рассмотрим процедуру расшифрования, выполняемую также с использованием полиномиальной системы. Как отмечалось ранее, для выполнения процедуры дешифрования используется выражение (14). Для вычисления корня степени х . из в з необходимо свести данную немодульную операцию к совокупности модульных. Исходя из условия (16), необходимо определить мультипликативную обратную величину (x j.) ¹ относительно х_j по модулю p ^ν - 1 . Для этого необходимо на приемной стороне использовать блок, позволяющий вычислить данную величину по значению х_j , поданному с выхода многотактового фильтра. В представленном примере для расширенного поля Галуа GF(2 ³ ) значения Х^-1 будут иметь следующий вид

Х ^-1 = {3, 6, 6,...}.

Осуществим операцию дешифрования с использованием и без полиномиальной системы классов вычетов.

Итак,полученный первый блок β₁(z)длиной 7 бит поступает на устройство,реализующее операцию дешифрования согласно (14).При этом с выхода блока вычисления обратной мультипликативной величины подается значение Х ₁ ^-1 = 3 в двоичном коде.В результате выполнения операции по модулю Р(z)получаем:

A (z) = x 1 P i (z) modP(z) =

= (z ⁶ + z ⁵ ) ^{- X|} modz ⁷ + 1 = (z ⁶ + z ⁵ ) ³ modz ⁷ + 1 =

= z ⁴ + z ³ + z ² + z = (0, z ² ,z + 1).

Реализуем процедуру дешифрования в 1 (z) в полиномиальной системе классов вычетов:

A (z) = ^x 1 (0,z ² + 1,z) modP(z) = |(0,z ² + 1,z) ³|* + 1 =

= (|03|+ |(z2 +1)3|+,      |z3|,    ) = z+1               z3 +z2 +1      z3 +z+1

= (0, z ² ,z + 1).

Аналогичным образом поступаем с последующими блоками зашифрованных данных в 1 (z) , в 2 (z) , в з (z).

Для блока в ₂ (z) получаем

^A 2 ^(z) = x ² p 2 (z) modP(z) = |(z ⁶ + z ² ) ^х 1+ 7 + 1 =

6.26 ⁺          6.5                     2

= (z + z )      = z + z + z + 1 = (0, z + z,1).

z ⁷ + 1

Воспользуемся полиномиальной системой класса вычетов для выполнения процедуры дешифрования

A 2 (z) = ^x J (0,z,1)modP(z) = |(0,z,1,z) ^ + 1 =

= (|0 61⁺ |z ⁶| +       1 ⁶| ,     ) = (0, z ² + z,1) .

z + 1        z ³ + z ² + 1       z ³ + z + 1

Проведем дешифрование блока P 3 (z) = z ⁴ + 1 :

A 3 (z) = ^x 3 p3 (z) modP(z) = |(z ⁴ + 1) - ^х ■ |+, +1 =

= |(z ⁴ + 1) 61 *    = z ³ + z ² + z + 1 = (0,z,z ² )

z ⁷ +1

При реализации дешифрования в полиномиальной системе класса вычетов получаем

A 3 (z) = ^x 3j в 3 (z) modP(z) =

(0,z ² + z,z ² + z + 1) ⁶ modz ⁷ + 1 =

= (061 + J(z2 + z)61 + 2 J(z2 + z +1)61+3    ) = z+1                    z3 +z2 +1                         z3 +z+1

= (0, z, z ² ).

Полученные результаты свидетельствуют о том, что при применении полиномиальной системы класса вычетов получается результат,аналогичный операции нелинейного шифрования с возведением в степень по модулю.

В ходе проведенных исследований было выявле-но,что применение полиномиальной системы классов вычетов для реализации нелинейного шифрова-нияпозволилоснизитьвременные затраты на 9,2%по сравнению с выполнением метода шифрования с возведением в степень по модулю в поле Галуа GF(2 3 ) . Следует отметить,что при увеличении разрядности обрабатываемых данных возрастает эффективность применения полиномиальной системы классов вычетов для реализации нелинейных криптографических процедур защиты данных от НСД.

Выводы

Проведенныеисследованияпоказали,чтосисте-мы поточного шифрования, использующие расширенные конечные поля, обладают более широкими возможностями по реализации различных криптографических функций обеспечения конфиденциальности и целостности информации. Применение в таких функциях различных операций, связанных со сложением, умножением, возведением в степень символов в конечном поле и их различных комбинаций и использование возможности генерации в конечном поле множества различных псевдослучайных последовательностеймаксимальнойдлины позволяет реализовать такие защиты информации, для которых наличие исходного и шифрованного текста не снижает криптостойкость системы. При этом применение полиномиальной системы классов вычетов позволяет повысить скорость выполнения процедур нелинейного шифрования.