Технология обработки сопровождающей измерительной информации для высоточной координатной привязки космических снимков

Качество получаемой космической наблюдательной информации существенно зависит от точности определения взаимного положения систем координат (СК), связанных с орбитальным телескопом (ОТ) и с основными измерительными приборами – астродатчиками (АД), жестко установленными на корпусе космического аппарата (КА). Для взаимной привязки этих СК организуется специальный режим, где выполняется сканирование телескопом звездного неба и одновременно фиксируются измерения оптико-электронных АД. Полученная при этом информация передается в наземный комплекс, где выполняется уточнение взаимного положения указанных СК и фактического положения телескопа относительно наземных объектов в процессе его маршрутного движения при оптико-электронной съемке, а также оформление космических снимков с высокоточной координатной привязкой к наземным объектам.

В типовой схеме съемочной системы сканирующего типа применятся набор ПЗС-матриц (линеек), расположенных в фокальной плоскости ОТ с небольшим взаимным перекрытием в продольном направлении и со сдвигом друг относительно друга в поперечном направлении. Такая конфигурация ПЗС-структур и законы съемки приводят к тому, что

• ♦    проекции ПЗС-матриц образуют на земной поверхности отдельные полосы со смещениями друг относительно друга в продольном и поперечном направлениях;

• ♦    величины продольных и поперечных смещений могут существенно изменяться на протя-

• Евгений Иванович Сомов, кандидат технических наук, доцент, заведующий отделом. E-mail: e_somov@mail.ru. Сергей Анфимович Бутырин, кандидат технических наук, ведущий научный сотрудник.

жении маршрута съемки;

• ♦    строка изображения, полученная сдвинутыми друг относительно друга в поперечном направлении ПЗС-матрицами, характеризуется своими индивидуальными параметрами движения съемочной системы, поэтому рассматривать изображения, полученные отдельными ПЗС- матрицами, как единое целое, можно только при учете общего набора кинематических параметров движения ОТ;

• ♦    космическим изображениям, полученным ОТ, присущи геометрические искажения, обусловленные панорамным эффектом, кривизной Земли, эллиптичностью орбиты, рельефом местности и другими факторами.

Большая часть указанных выше искажающих факторов имеется также и при кадровой съемки.

Наземные комплексы (центры) обработки космических снимков заказывают получение непосредственно с борта КА только предварительно обработанную электронную видеоинформацию по строго заданному наземному участку, дополненную сопровождающей (служебной) информацией о фактических условиях космической съемки, весьма часто без опорных (реперных) наземных объектов.

В статье кратко представляется компьютерная технология, основанная на разработанных инновационных методах уточнения фактической ориентации ОТ при реализации их в процессе апостериорной обработке сопровождающей измерительной информации от системы астродатчиков.

СИСТЕМЫ КООРДИНАТ И РЕШАЕМЫЕ ЗАДАЧИ

Вводятся базисы, составленные из ортов, и системы координат (СК):

• ♦    инерциальная (ИСК) I _⊕ ( O _⊕ X _I ^e Y_I ^e Z _I ^e ) с началом в центре Земли O _⊕ ;

• ♦    Гринвичская геодезическая (ГСК) E _e

( O _$ X^eY^eZ^e ), которая вращается относительно ИСК с вектором угловой скорости ю _е ^ to _e ;

• ♦    горизонтная (ГорСК) E h ( Cx Ch Y ^h z Ch ) с началом в точке C и эллипсоидальными геодезическими координатами – высотой H_c , долготой L_c и широтой B_c ;

• с вязанная с КА (ССК) B ( O xyz ) в его центре масс O ;

• о рбитальная система координат (ОСК) O ( O x^oy^oz^o );

• ♦    базис S = { s 1 , s ₂ , s ₃ } и СК оптического телескопа (ОпСК) O x^s y^sz^s ;

• С К поля изображения (ПСК) O_i x ⁱ y ⁱ z ⁱ с началом в центре O_i фокальной плоскости yⁱO_i zⁱ ;

• ♦    визирная СК (ВСК) V = { v 1 , v ₂ , v ₃ } ( O v x v y v z v ) с началом в центре O _v матрицы ПЗС в фокальной плоскости yⁱO_izⁱ телескопа, причем точки O i и O _v считаются совпадающими, а орты s 1 базиса S и v 1 базиса V - строго противоположными;

СК p -го астродатчика (СКА _p ) A p = { a p , b p , c p } ( O x p y p z p ) связана с ПЗС в его фокальной плоскости, p = 1,2,3,4 = 1 + 4, при этом угловое положение СКА _p фиксировано в ССК, орты a _p оптических осей астродатчиков принадлежат поверхности конуса с некоторым узлом полураствора, но их фактическое положение в ССК точно не известно;

виртуальная (расчетная) система координат астросистемы (СКАС) A = { a 1 , a ₂ , a ₃ } ( O x ^a y ^a z ^a ), вычисляемая на основе обработки доступной измерительной информации от произвольной комбинации астродатчиков.

Для простоты будем считать базисы B и S (ССК и ОпСК) совпадающими. Графическое отображение указанных СК представлено [1].

Состояние ССК относительно ИСК определяется кватернионом Л и вектором угловой скорости го . При известных пространственных координатах орбитального движения центра масс КА решаются задачи:

определения углового положения базиса S и фиксированного взаимного углового положения базисов V и S в режиме астрономического контроля согласования осей (АКСО), когда используется измерительная информация только от телескопа;

определения фиксированного взаимного углового положения базисов A и S , когда используется измерительная информация, полученная в режиме АКСО как от телескопа, так и от астродатчиков;

• ♦    уточнения кватерниона Л ( t ) фактического углового положения (при необходимости и вектора фактической угловой скорости го ( t ) ) базиса S относительно инерциального базиса I = I _$ для любого момента времени t е T n = [ t i , t _f ] из заданного интервала T n длительностью

T n = t _f — t i в режиме оптико-электронной съемки телескопом заданного участка поверхности Земли, когда используется измерительная информация только от астродатчиков.

МЕТОДЫ СГЛАЖИВАНИЯ ДИСКРЕТНЫХ ИЗМЕРЕНИЙ

Классическая задача полиномиальной аппроксимации значений y s = f ( x s ), s = 1 + n неизвестной скалярной функции y = f ( x ) полиномом y = ^ ax' степени m <  n по методу наименьших квадратов (МНК) состоит в определении коэффициентов a ,-, 1 = 0 + m из условия Ё { (j a i x ) — y s }² ^ min . ¹                                                  s = 1 i = 0

Степень m аппроксимирующего по МНК полинома должна выбираться с учетом размера выборки y_s = f ( x_s ), s = 1 + n , т.е. значения n . Решение практических задач [2] показывает, что при больших значениях n рационально применять метод (фильтр) полиномиального сглаживания Савицкого – Голея [3], который является модификацией МНК. Здесь выполняется аппроксимация последовательности дискретных значений y_s = f ( x_s ) в “скользящем” окне (кадре) длины n * <<  n , где n * является целым нечетным числом, также “скользящим” полиномом небольшого порядка m , например _m = 3 . Первый кадр формируется из значений y_s = f ( x_s ), s = 1 + n * , начиная с первого измерения, и для него по МНК строится полином заданного порядка. Далее кадр сдвигается на 1 отсчет и вновь выполняется аппроксимация. Всякий раз в выходную последовательность записывается единственное значение аппроксимирующего полинома, соответствующее центру ( n * — 1) / 2 текущего положения “скользящего” кадра. Исключениями являются первый и последний кадры, когда выходные значения процедуры сглаживания получаются в точках полиномов, соответствующих первой и последней половинам крайних кадров. Сглаживание значений трехмерной векторной функции y _s = f ( x_s ), s = 1 + n скалярного аргумента с помощью фильтра Савицкого–Голея реализуется стандартным применением данной процедуры для значений каждого компонента вектора-столбца из отображений значений векторной функции на оси некоторого ортогонального базиса.

Более сложной является задача определения взаимной ориентации двух ортогональных базисов на основе данных о произвольного расположенных в них двух наборов ортов. Пусть заданы совокупность ортов bi , измеренных в связанном базисе B , и совокупность значений соответствующих им ортов ri , заданных в инерциальном базисе I . Классическая задача векторного согласования (vector matching – задача Wahba) формулируется так: най- ти ортогональную матрицу A с определителем, равным +1, которая минимизирует квадратичный критерий L(A) = 15ai | bi - Ari |2, где неотрицательные числа ai являются весовыми коэффициентами. Решением этой задачи является оптимальный кватернион л, который эквивалентен искомой ортогональной матрице A и определяется как нормализованный собственный вектор матрицы K с наибольшим собственным значением q , т.е.

max

к л =

q max

Л ;

к =

tr B

z

z *

S - I ₃tr B

;

B = 5 a i b i r i ¹; S = B + B * ; z = 5 a i b i x r i . (1)

Соотношения (1) представляют собой алгоритм QUEST (Quaternion Estimation) [4] оценки кватерниона, который применяется в представляемой методике для обработки измерительной информации, полученной в режиме АКСО.

Кватернион Л = ( X ₀ , X ) взаимно-однозначно связан с вектором о модифицированных параметров Родрига (далее просто вектора Родри-га) явными аналитическими соотношениями

о = Х/ (1 + Х ₀ );     Х = 2 о /(1 + о ²);

Х о = (1 -о ²)/(1 + о ²)         ’    ⁽²⁾

общеизвестным прямым и обратным кватернионным кинематическим уравнениям соответствуют прямые и обратные векторные кинематические уравнения для вектора Родрига:

1       _2х о = -(1 -о )® + -ох® + -о<о,ю >;

4    ²²

® =

4[(1 - о ²) о - 2 ( о x о ) + 2 о <  о , о > ] (1 + о ²)²

Эти соотношения позволяют свести задачи сглаживания кватернионных данных к обычной задаче сглаживания векторных измерений. Экстраполяция дискретно заданных значений кватерниона Л k осуществляется с применением вектора Родрига о и аналитических соотношений (2).

ОПРЕДЕЛЕНИЕ ОРИЕНТАЦИИ ТЕЛЕСКОПА И ВСК В АКСО

При сканировании звездного поля с постоянной угловой скоростью to z « 0.015 ^o / c относительно оси тангажа и организации “скользящего окна” с полем зрения телескопа со строго фиксированной частотой накопления зарядовых пакетов электронного изображения вдоль столбцов матрицы ПЗС получаются последовательности значений как кватерниона Л V ориентации ВСК, так и кватерниона Л $ ориентации ОпСК относительно ИСК. Орт s 1 базиса S и орт v 1 базиса V считаются строго противоположными, поэтому сначала определяется последовательность

значений кватерниона ориентации Л ® оптического базиса S = { s_b s 2 , S 3 } телескопа с точной привязкой к моментам времени t_s по снимку звездного неба на основе следующей методики. Вся последовательность N распознанных звезд на снимке разбивается на группы (кадры) так, чтобы в каждом кадре (окне) было заданное нечетное число звезд n по следующим правилам:

звезды располагаются в порядке возрастания моментов времени t_s их регистрации без пропусков;

каждый последующий кадр включает только одну дополнительную звезду.

Каждый i -ый кадр “привязывается” к моменту времени t™ по его центральной звезде с номером i . Далее для каждого кадра определяются два набора ортов направлений на звезды: набор ортов r j в ВСК по относительным координатам звезд в фото-приемной плоскости матрицы ПЗС и набор ортов b j в ИСК по прямым восхождениям a _v и склонениям 5 _v , _v = 1 + n звезд (по звездному каталогу FK-5). В завершении вызывается процедура QUEST для определения массива значений кватерниона Л S ориентации ОпСК относительно ИСК в моменты времени t ™ , i = 1 + N k , где N k - число кадров на снимке. Полученные в [1] результаты свидетельствуют, что для обеспечения допустимой погрешности определения фактического положения оптической оси телескопа в ИСК достаточно десяти наблюдаемых звезд в кадре. Погрешность же определения разворота 5ф _x вокруг оптической оси телескопа в десятки раз хуже даже при большом числе звезд, что обусловлено малым полем зрения телескопа – недостаточной измерительной базой.

Разработанная методика уточнения положения базиса S относительно инерциального базиса I основывается на расширении измерительной астрономической базы за счет продолжительного сканирующего движения КА с угловой скоростью to Z » 0.015 ^o / c по каналу тангажа, возможно с технологическими перерывами в части наблюдения телескопом звезд: допускается возможность движения телескопа с закрытой крышкой. Например, при общем временном интервале сканирования длительностью 1000 сек достаточно получать изображения звезд только на трех участках длительностью 100 сек – в начале, в середине и в конце общего временного интервала. В итоге при угловой скорости ® * « 0.015 ^o / c перемещения оптической оси телескопа в “плоскости сканирования” получается измерительная астрономическая база с угловым размером 15 ⁰ . Как показали численные расчеты с применением фильтрации оценок кватерниона ориентации телескопа (точнее, оценок вектора Родрига) по методу Савицкого–Голея, такой измерительной

базы вполне достаточно для восстановления фактического положения базиса S относительно базиса I при среднеквадратичном отклонении (СКО) в определении разворота 5ф _х вокруг оптической оси телескопа не более 1 угл. сек.

Когда используется измерительная информация только от телескопа, определение фиксированного взаимного углового положения базисов V и S (их взаимного разворота относительно орта s 1 = — v 1 ) выполняется на основе специального дополнительного анализа номеров столбцов матрицы ПЗС, на выходе которых появляются накопленные изображения звезд в периферийной части линеек ПЗС. При этом удается определить постоянные технологические погрешности установки матрицы ПЗС в фокальной плоскости телескопа, которые в дальнейшем учитываются при планировании наблюдений заданных участков земной поверхности.

ОПРЕДЕЛЕНИЕ ОРИЕНТАЦИИ АСТРОСИСТЕМЫ В АКСО

Виртуальная СКАС A = { a 1 , a ₂ , a ₃ } вычисляется на основе обработки доступной измерительной информации, полученной в режиме АКСО от произвольной комбинации астродатчиков. Матрицы ПЗС в фокальной плоскости каждого АД фиксированы в ССК, поэтому “суммарное” поле зрения астросистемы на базе любой комбинации из не менее двух астродатчиков составляет измерительную астрономическую базу, вполне достаточную для высокоточного определения положения виртуальной СКАС относительно того же инерциального базиса I . Наилучшие результаты получаются при доступности измерительной информации от всех четырех АД и ее последующей бортовой обработки, сначала с помощью алгоритма QUEST и далее фильтрации по методу Савицкого–Голея. В другом предельном расчетном случае виртуальная СКАС строится на основе информации только об угловом положении в ИСК ортов a _p оптических осей любых двух АД. При наличии оценок кватерниона ориентации ВСК и кватерниона ориентации виртуальной СКАС относительно одного и того же инерциального базиса получается поправочный кватернион для учета их взаимного положения.

УТОЧНЕНИЕ ОРИЕНТАЦИИ ВСК ПРИ НАБЛЮДЕНИИ ЗЕМЛИ

Уточнение значений кватерниона Л ( t ) фактического углового положения и вектора фактической угловой скорости ю ( t ) базиса S относительно инерциального базиса I для любого момента времени t е T _n = [ t i , t _f ] в режиме оптико-электронной съемки ОТ заданного уча-

стка поверхности Земли, когда используется измерительная информация только от астродатчиков, является весьма непростой задачей.

Выполненная в режиме АКСО калибровка взаимного углового положения ВСК и виртуальной СКАС сначала проверяется в режиме наблюдения наземных полигонов с известными опорными объектами. Необходимость такой дополнительной калибровки обусловлена различием в условиях наблюдения “холодного” космоса и “теплой” Земли. В этом режиме калибровки система управления ориентацией КА реализует программное угловое движение телескопа в ИСК, заданное набором векторных сплайнов, которые рассчитываются из условий наблюдения полигона с назначенным азимутом сканирования.

Вычисление программных значений кватерниона ориентации Л и вектора ю , как явных функций времени, выполняется на основе векторного сложения всех элементарных движений телескопа (ОпСК) в ГСК с учетом текущей перспективы наблюдения при задании начальных координат наземного объекта и потребного азимута сканирования. Пусть векторы-столбцы ю s и v _e ^s представляют в ОпСК соответственно угловую скорость и скорость движения центра масс КА относительно ГСК, матрица C = || ^у у || определяет ориентацию ОпСК относительно ГорСК и скалярная функция D ( t ) представляет дальность наблюдения вдоль оси визирования. Тогда для произвольной точки (^у1 , ~ ¹ ) в фокальной плоскости телескопа компоненты

1 у1 1 1 у y = Vy(У ,z ) и ~ = V(y ,y1) векторанормиро-ванной скорости движения изображения вычисляются по векторно-матричному соотношению

' У1

~ ¹

У ¹

~ 1

z

i~s ~i q ve1 - У

'e । ~ s,^s ^Ю e 3 + Z Ю e 2

q ve2 — is q ve1 +

^Ю e 3 ^{— Z Ю} e 1

ю e 2 + У ю e 1

Здесь ^{у 1} = y ¹ / f e и У ¹ = z¹ / f e являются нормированными фокальными координатами указанной точки, где f_e – эквивалентное фокусное расстояние телескопа, скалярная функция q ¹ = 1 — ( c ₂₁ y + c ₃₁ z^l)lС 11 и компоненты вектора нормированной скорости поступательного движения y es. = v S ( t )/ D ( t ), I' = 1,2,3 , где D ( t ) - наклонная дальность наблюдения. На основе (4) получаются искомые программные значения компонентов вектора-столбца ю S , в явном виде при кадровой съемке (слежении) и с помощью единственного численного интегрирования уравнения для вектора Род-рига (3) при сканирующей съемке. В последнем случае набором векторных сплайнов 3 порядка выполняется высокоточная интерполяция программных значений кватерниона Л ( t ) и вектора ю ( t ).

Фактическая последовательность положений

ВСК относительно ИСК в процессе съемки наземного полигона получается по методу обратной динамической фотограмметрической засечки – с использованием точной привязки к моментам времени t_s появляющихся на снимке изображений опорных (реперных) объектов полигона. Здесь применяется методика, аналогичная представленной выше методике определения углового положения ВСК относительно ИСК в режиме АКСО.

Сопровождающая снимок измерительная информация от астросистемы обрабатывается с помощью алгоритма QUEST, фильтрации по методу Савицкого–Голея и экстраполяции векторными сплайнами. При этом оценка вектора угловой скорости ю ( t ) базиса S относительно ИСК получается по обратному векторному кинематическому уравнению для вектора Родрига (3) на основе дифференцирования векторного сплайна по явным аналитическим соотношениям.

Рассогласование между оцененным с помощью астросистемы и фактическим (по снимку полигона) движениями ВСК относительно ИСК дает с одной стороны оценку точности восстановления фактической ориентации ВСК в процессе съемки наземного участка, а с другой стороны – возможность уточнить постоянный поправочный кватернион для учета взаимного положения виртуальной СКАС и ВСК. После выполнения калибровки по наземным полигонам бортовые средства КА готовы для решения задач апостериорного уточнения (восстановления) фактического углового положения и вектора фактической угловой скорости ВСК для любого момента времени оптико-электронной съемке орбитальным телескопом произвольного участка земной поверхности, когда используется информация только от астросистемы.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

В данном разделе приводятся некоторые результаты отработки представляемой технологии на модельных задачах.

Моделирование режима АКСО

Данные для расчетов. Эквивалентноефокус-ное расстояние телескопа f e = 10 м; суммарная длина линейки ПЗС l e = 0.5 м; размер пикселя r p = 10 мкм; погрешности привязки шкалы времени д t = io ^{- 4} с; погрешности определения энергетического центра звезды на снимке д r = 5 пикселей; длительность маршрута АКСО T ma = 200 с; заданная продольная скорость движения изображения у * = 5 мм/с; кватернион начальной ориентации ВСК относительно ИСК

Л ( t ₀ ) = {0.9689124217, 0.0661214 894,

-0.1983644682, 0.1322429788}.

Программное движение в АКСО соответствует вращению ОТ с постоянной скоростью m Z = V * / f e относительно оси Oz ВСК от положения Л ( t ₀ ) . Ниже кратко приводятся результаты, полученные на основных этапах реализации предлагаемой технологии.

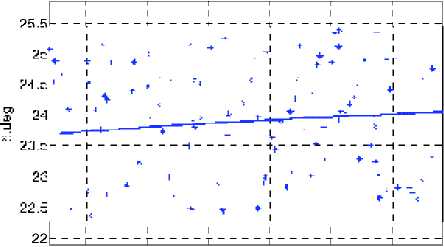
• 1.    Наблюдение звезд и получение снимка, рис. 1.

• 2.    Разбиение снимка на кадры (в этом примере число звезд в кадре m = 29 ) и восстановление кватерниона Л q ( t i ), i = 1 ^ n ориентации ВСК относительно ИСК алгоритмом QUEST, где t _i – моменты времени регистрации звезд. Угловые рассогласования 5ф ( t i ) = 2усс1( Л p ( t i ) о Л q ( t i )), i = 1 ^ n по осям ВСК между программным Л p ( t i ) и восстановленным Л q ( t i ) по снимку кватернионами представлены на рис. 2. Как отмечено выше, всегда наибольшие погрешности в восстановлении ориентации ОТ проявляются относительно оптической оси телескопа.

• 3.    Преобразование восстановленного кватерниона Л q ( t i ) в параметры вектора Родрига и фильтрация по методу Савицкого-Голея с окном _m = 17 полиномом 3 порядка, результат о f ( t i ), i = 1 + n , определение кватерниона Л f ( t i ) . Угловые рассогласования 5ф ( t i ) = 2усс1( Л p ( t i ) о Л f ( t i )), i = 1 + n по осям ВСК между программным и отфильтрованным Λ f кватернионами представлены на рис. 3.

• 4.    Восстановление вектора фактической угловой скорости: ° f ⁽ t i ) = ⁽ ° f ⁽ t i + 1 ) ° f ⁽ t i ^))/( t i + 1 - t i ); ю ( t i ) = f ( о f ( t i ), о f ( t i )). Вектор ю s восстановленной угловой скорости определяется по компонентам j как среднее арифметическое ю j ( t i ), j = 1 + 3 на множестве моментов времени t_i . Отклонение вектора ω _s от программного значения представлено на рис. 4.

• 5.    Разделение углового движения на 2 составляющие: движение с постоянной угловой скоростью с кватернионом ^Л s ⁽ t i ) = ^Л 0 ^{о [cos(} ® s t i I ²⁾ ; ^{( ю} s ^{1 ю} s ) ^sin( ® s t i I ^{2)] и} отклонение от него с кватернионом 5 Л s ( t i .) = Л s ( t i .) о Л ( t i .).

• 6.    Выполняется простейшая линейная аппроксимация кватерниона отклонения 5 Л _s ( t i ) с применением вектора Родрига. В результате получается аналитическая функция Л ( t ) = Л _s ( t ) о 5 Л _s ( t ) восстановленного кватерниона ориентации ВСК, заданного значениями Л 0 , ю s и коэффициентами a i , b i ,i = 1: n - 1 на массиве дискретных значений 1 1 ^ t i .< t n = 1 0 + T .

Погрешности определения ориентации ВСК по каналам в этом примере составили: СКО о x = 7", о y = 0.15", о z = 0.16", математическое ожидание m x =- 4", m y = 0.05", m z = 0.07".

Определение взаимной ориентации виртуальной СКАС и телескопа

Исходные данные. Пусть имеется два астродатчика, выходные сигналы которых соответствуют измеренным значениям ортов оптических их осей

15      16      17      18      19      20

a,deg

Рис. 1. След оси Ox ВСК и наблюдаемые 111 звезд на небесной сфере

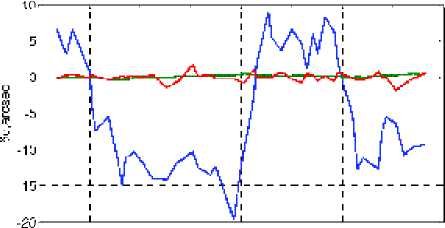
20     40     60     80     100    120    140    160    180

t, S

Рис. 2. Угловые рассогласования Зф ( t i ) по осям ВСК между программным

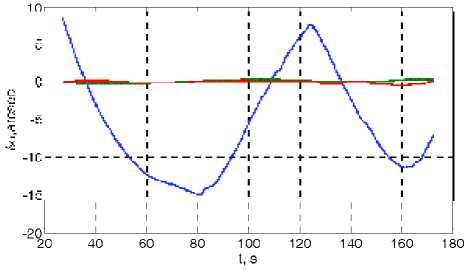
Рис. 3. Угловые рассогласования по осям ВСК между программным и отфильтрованным кватернионами

и восстановленным кватернионами

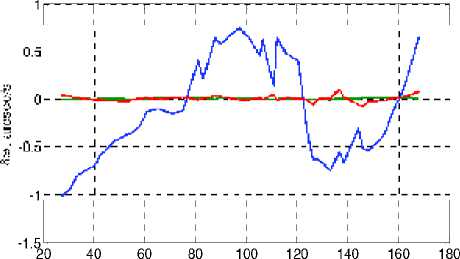
t, s

Рис. 4. Отклонение угловой скорости от программы

a 1 , a ₂ в ИСК. Обозначим выходные сигналы АД как a ⁰ = a ₀ i + A a ₀ i , a i = a ⁰ / a ⁰, i = 1,2 , где A a i = { ^ i , i = 1 ч 3}, a ^ i - случайные числа, распределенные по нормальному закону с нулевым математическим ожиданием и СКО= (2 /(3д/3)" - Пусть оптические оси АД конструктивно отклонены от оси визирования Ox телескопа на углы ± 30⁰ в плоскости xOz ВСК, а частота измерений АД составляет 4 Гц. Если построить виртуальную СКАС на измерениях АД с такими направлениями осей: Oz – по векторному произведению ортов a 1 и a ₂ , Ox - по сумме ортов a 1 и a ₂ , а Oy - дополнением до правой тройки, то в номинале виртуальная СКАС совпадает с номинальным положением ВСК.

• 1.    Моделирование измерений АД и построение виртуальной СКАС в двух вариантах: в номинальном положении и по фактическим измерениям в виде кватернионов Л _v ( t i ) - Далее следует определение вектора малого углового рассогласования 5ф = 2vect ( Л _p ( t i ) о Л _v ( t i )), i = 1 ч n . Полученные результаты представлены на рис. 5.

• 2.    Фильтрация значений кватерниона Л _v ( t i ) фильтром Савицкого-Голея с окном m = 17 и полиномом 3 порядка. С помощью полученного результата Л _v f ( t i ) далее определяется угловое рассогласование 5ф ( t i ) = 2vect( Л p ( t i ) о Л v f ( t i )), i = 1: n , см. рис. 6.

• 3.    Для моментов времени измерений астродачи-ков по значениям ^Л 0 , “ 5 и коэффициентов

a i , b i , i = 1 ч ( n - 1) вычисляется массив значений кватерниона ориентации ВСК Л ( t k ), к = 1 ч N и определяются отклонения виртуальной СКАС от визирной СК 5 Л ( t k ) = Л _p ( t k ) о Л _v f ( t k ), к = 1 ч N . Полученный при этом результат в вектора углового отклонения Зф ( t k ) = 2vect( 5 Л ( t k )) представлен на рис. 7.

Полученные в результате расчетов погрешности определения взаимной ориентации по каналам составили: СКО ст x = 6".8, ст _y = 0".19, ст z = 0".1б , математическое ожидание m x = 5".7, m y = 0".03, m z = 0".07 . Здесь также рассчитывается постоянный поправочный кватернион.

Восстановление внешнегоориентирования телескопа

Данные для расчетов

• 1)    Массивы кватернионов Л ( t i ) и угловых скоростей го ₅ ( t i ), t = 1 ч n на 2-х маршрутах, каждый длительностью 30 сек. Первый маршрут – съемка в надире, метод съемки – с постоянной ориентацией оси визирования ОТ в ОСК, максимальное значение модуля вектора угловой скорости в ИСК не превосходит 0.6 град/c. Второй маршрут – съемка поперек трассы, метод съемки – с выравниванием продольной скорости движения изображения в центре фокальной плоскости ОТ, максимальное значение модуля вектора угловой скорости в ИСК не превосходит 0.8 град/c.

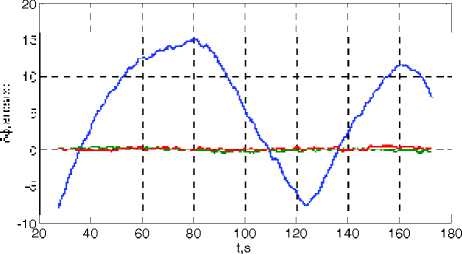
Рис. 7. Взаимные отклонения ВСК и виртуальной СКАС

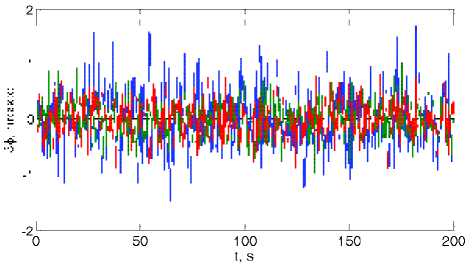
Рис. 5. Измеренные отклонения виртуальной СКАС

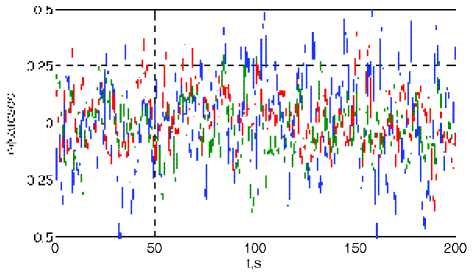
Рис. 6. Отклонение виртуальной СК после фильтрации

• 2)    Известен кватернион перехода из виртуальной СКАС в ВСК, определенный и уточненный в режиме АКСО.

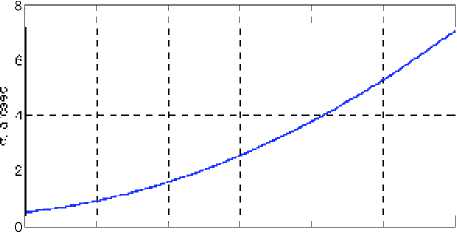
• 3)    Характеристика СКО погрешностей измерений АД в зависимости от модуля угловой скорости представлена на рис. 8.

• 1.    Моделирование измерений АД, представленных значениями ортов a ₁ ( t_i ),a ₂ ( t_i ) и построение кватерниона Λ_Ι^vi( t_i ) ориентации виртуальной СКАС относительно ИСК в моменты измерений t_i , i = 1 ÷ N . Полученные при этом результаты без фильтрации представлены на рис. 9 только для маршрута 2, как более напряженного.

• 2.    Фильтрация значений кватерниона Λ_Ι^vi( t_i ) , результаты для маршрута 2 представлены на рис. 10.

• 3.    Определение ориентации ВСК относительно ИСК, погрешности такого определения по оси Ox и осям Oy , Oz для маршрута 2 приведены на рис. 11 и рис. 12 соответственно.

На завершающем этапе выполняется аппроксимация углового движения ОТ векторными сплайнами третьего порядка и формирование значений кватерниона Λ _Ι^v ( t_k ) в любые требуемые моменты времени t_k , k = 1 ÷ K , с оценкой угловых элементов внешнего ориентирования и скоростей движения изображения в каждом пикселе матрицы ПЗС с применением универсального соотношения (4) . При высоте полета КА ≈ 600 км погрешности δ = m ± 3 σ (матожидание m ± утроенное СКО 3 σ ) привязки координат космических снимков в плане, измеряемые в метрах, как по отдельным каналам δ _x , δ _yz , так и в целом δ _r , были оценены в конечном итоге такими значениями:

маршрут 1:

δ x = 0.44 ± 0.024, δ _yz = 0.29 ± 1.92, δ r = 0.53 ± 1.92; маршрут 2:

δ _x = 0.43 ± 0.048, δ _yz = 0.27 ± 1.98, δ _r = 0.55 ± 1.98.

Таким образом, на тестовых задачах получена высокая точность привязки космических снимков к наземным объектам без опорных точек, что показывает эффективность предложенной технологии.

О 0.5         1          1.5         2         2.5         3

го, deg/s

Рис. 8. Характеристика СКО погрешностей измерений АД

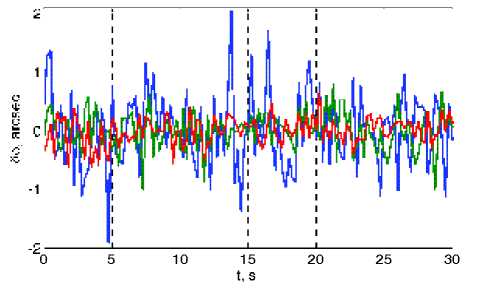
Рис. 9. Отклонение СКАС от номинала на маршруте 2

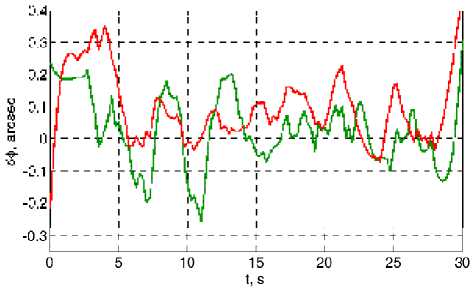
Рис. 12. Погрешности восстановления по осям Oy , Oz

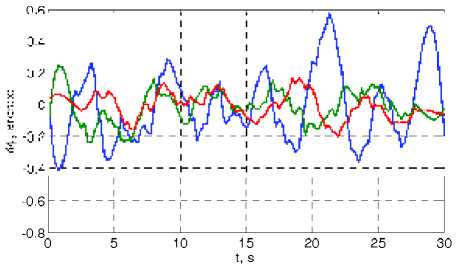
Рис. 10. Отклонение СКАС от номинала после фильтрации

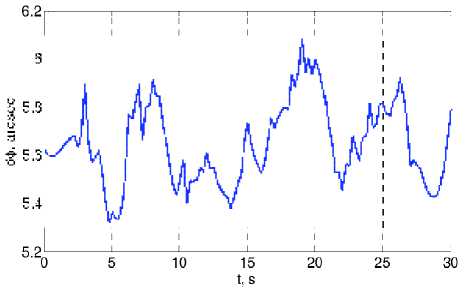
Рис. 11. Погрешность восстановления

ориентации по оси Ox

ЗАКЛЮЧЕНИЕ

Кратко представлена технология и разработанные инновационные методы для уточнения фактической ориентации орбитального телескопа на основе апостериорной наземной обработки сопровождающей измерительной информации. Эти методы основаны на известных приемах сглаживания – аппроксимации, фильтрации векторных измерений и интерполяции результатов фильтрации векторными сплайнами. Представлены некоторые конкретные численные результаты, демонстрирующие эффективность предложенной технологии.

Работа поддержана РФФИ (грант 08-0899101) и Отделением энергетики, механики, машиностроения и процессов управления РАН (программа 15).