Технология оперативной реконструкции трёхмерных сцен по разноракурсным изображениям

Задача реконструкции трёхмерных моделей сцен по разноракурсным изображениям является крайне востребованной в различных приложениях [1, 2]. При этом часто ставится задача восстановления 3D-сцен в реальном времени. Такие требования часто возникают при обработке данных ДЗЗ, например, с целью мониторинга чрезвычайных ситуаций, построения цифровых моделей местности (ЦММ) для анализа фоноцелевой обстановки и др. При этом к программным комплексам, решающим эти задачи, часто предъявляется также требование низкой стоимости и компактности исполнения. Поэтому актуальной является задача построения экономичных по требуемым вычислительным ресурсам технологий оперативной реконструкции 3D-сцен по разноракурсным изображениям.

Центральной проблемой в технологиях восстановления трёхмерных сцен по разноракурсным изображениям является нахождение соответствующих точек на разных видах. При решении этой задачи на изображениях с большими относительными сдвигами область поиска соответствующих фрагментов должна быть значительно увеличена. Это приводит как к повышению вычислительной сложности и увеличению времени поиска, так и к снижению надёжности определения соответствующих точек. В какой-то степени область поиска можно сузить, если сопоставление изображений осуществлять по ректифицированным изображениям [3]. Недостатком такого подхода является внесение дополнительных искажений при интерполяции отсчётов изображения в ходе ректификации.

В работе [4] рассматривалась технология, не требующая предварительной ректификации изображений. В рамках этого подхода соответствующие точки ищутся на соответствующих эпиполярных линях, для определения которых используется фундаментальная матрица. Если параметры камер (внутренние и внешние) известны, фундаментальная матрица может быть вычислена с использованием этих параметров. В ситуации, когда параметры камер не известны, фундаментальная матрица может быть оценена по небольшому числу (не менее семи) соответствующих точек на изображениях двух видов. В работе [5] рассматривалась реализующая этот подход информационная технология реконструкции ЦММ по стереоизображениям. Эта технология позволяет существенно сократить объём вычислений, однако не снимает всех проблем. Область поиска вдоль эпиполярных линий всё равно остаётся значительной при больших начальных относительных сдвигах и в особенности при различиях масштабов сопоставляемых разноракурсных изображений.

Цель настоящей работы – повышение качества восстановления трёхмерных сцен за счёт введения в технологию, рассмотренную в [5], дополнительного этапа начального совмещения разноракурсных изображений, а также существенное повышение быстродействия алгоритмов за счёт распараллеливания и реализации в CUDA среде на гибридных вычислительных устройствах, включающих графические процессоры. Приводятся результаты экспериментальных исследований, иллюстрирующие как повышение качества, так и значительное сокращение времени реализации сквозной технологии реконструкции 3D-сцен.

Описание основных этапов технологии

Общая схема основных этапов предлагаемой технологии реконструкции 3D-сцены по разноракурсным изображениям приведена на рис. 1. Эта технология отличается от технологии, рассматривавшейся в работе [5], наличием дополнительного этапа начального совмещения разноракурсных изображений. Необходимо подчеркнуть, что, строго говоря, разноракурсные изображения, тем более отличающиеся масштабом, совместить точно невозможно, поскольку локальные сдвиги соответствующих точек, которые на сцене не принадлежат одной плоскости, зависят от ракурса съемки. Поэтому на данном этапе речь идёт о совмещении некоторых средних «сечений» сцены.

• 1.    Предварительное совмещение, масштаб и сдвиг

• 2.    Предварительный поиск сдвигов для нахождения фундаментальной матрицы

• 3.    Идентификация фундаментальной матрицы

• 4.    Нахождение иготовых относительных сдвигов

• 5.    Формирование карты диспарантности

Рис 1. Схема этапов технологии

Этап предварительного совмещения предлагается осуществлять с помощью аффинного преобразования с тремя степенями свободы. В данном случае это преобразование учитывает сдвиг и изменение масштаба

и задаёт соотношения между точками некоторого сечения сцены, зарегистрированной соответственно на первом – ( x, y ) и втором – ( x’, y’ ) изображениях:

m

m

d ₁

d ₂

x

y

г

x

y

где коэффициент m определяет масштаб, а d ₁ и d ₂ за-

дают сдвиг.

Для нахождения параметров аффинного преобразования m , d 1 и d 2 в данном случае решается переопределённая система уравнений. В качестве известных исходных данных используются координаты соответствующих точек ( x, y ) и ( x’, y’ ), которые предварительно находятся, например, методом SIFT [6] или SURF [7], которые признаны в настоящее время наиболее эффективными. Для того, чтобы аффинному преобразованию подвергалось наиболее характерное сечение сцены, для его определения желательно использовать, по возможности, большое число соответствующих точек. В этом случае для решения переопределённой системы уравнений целесообразно воспользоваться алгоритмом RANSAC. Известно, что этот алгоритм является устойчивым к грубым ошибкам типа сбоев и обеспечивает высокое качество определения модели при большом числе наблюдений.

В ситуации, когда число соответствующих точек невелико (при малом числе информативных фрагментов на изображениях), более высокое качество определения параметров аффинного преобразования даёт метод согласованной идентификации. Исследованию этого факта в задачах определения параметров по малому числу наблюдений посвящены работы [8], [9].

Введение дополнительного этапа начального приближённого совмещения разноракурсных изображений обеспечивает существенное повышение надёжности и быстродействия последующих этапов, рассматривавшихся в работе [5]. В частности, это позволяет сущест-

венно повысить быстродействие этапа сопоставления с использованием так называемой пирамиды изображений. Этот этап, по существу, также решает проблему устранения больших относительных сдвигов. Однако если сдвиги и разница масштабов велики, реализация алгоритма пирамиды изображений имеет либо высокую вычислительную сложность, либо низкую надёжность вследствие большой высоты пирамиды.

Алгоритм пирамиды изображений применительно к двум разноракурсным изображениям, подвергшимся совмещению с помощью аффинного преобразования, строится в виде иерархической схемы вычислений. Пирамида изображений формируется в виде набора изображений, получаемых уменьшением разрешения в два раза по обеим координатам. Таким образом, на N -м уровне пирамиды формируется изображение, разрешение которого в 2 ^N раз меньше исходного разрешения. Число уровней пирамиды устанавливается пользователем в виде параметра. На первом шаге данного этапа обрабатывается изображение с наименьшим разрешением. При этом начальный сдвиг принимается равным нулю. При поиске соответствий на следующем шаге используется информация о сдвиге, найденном на предшествующем шаге, т.е. на каждом следующем шаге значения координат удваиваются.

Найденные описанным выше способом соответствующие точки используются для определения фундаментальной матрицы. Также как и при определении параметров афинного преобразования, на этапе начального совмещения разноракурсных изображений для определения параметров фундаментальной матрицы при большом числе найденных соответствующих точек используется алгоритм RANSAC, а при малом числе точек – метод согласованной идентификации.

На следующем этапе осуществляется детальный поиск соответствующих точек для построения карты диспарантности. Основная проблема сопоставления изображений на данном этапе состоит в том, что на изображениях видов могут быть значительные малоинформативные области (фона). При этом известные эффективные алгоритмы определения соответствующих точек, например, детектор Харриса [10] с дальнейшим сравнением с использованием признаков SIFT [6] или SURF [7], а также алгоритм SimpleFlow [11] оказываются неработоспособными. В данном случае используется метод, предложенный в работе [5]. Метод основан на использовании расстояния до эпиполярной линии в качестве штрафного коэффициента в минимизируемой функции. Привёдем краткое описание этого метода.

Обозначим координаты точек на первом изображении ( u, v ), а координаты соответствующих им точек на втором – ( u + ∆ u , v + ∆ v ), где ∆ u , ∆ v – относительные сдвиги координат u , v соответственно. Пусть I ( u, v ) и I’ ( u + ∆ u, v + ∆ v ) – функции распределения яркости отсчётов на этих изображениях.

Задача состоит в поиске для каждой точки ( u, v ) на первом изображении соответствующей точки ( u + ∆ u ,

v + A v ) на втором изображении посредством минимизации критерия сходства:

E ( и 0 , v 0 , A u , A v ) =

I    a (u, v )|I (u, v) -1 ‘(u + A u, v +

( u , v ) e D ( u 0 , v 0 )

где D ( u 0 , v 0 ) – заданная область вокруг точки ( u 0 , v 0 ), а a ( u 0 , v 0 ) – весовая функция, задаваемая в указанной области в виде произведения трёх коэффициентов:

a (u, v ) = Wc • Wd • Wf , где wd = exp {-||(u 0,v0)-(u, v )| 12} , wd = exp {-| II ( u 0,v0)-1'( u, v )| 12} ,

I au ‘ + bv ‘ + c| wd = exp i—I , , t.

[ ^a ² + b ²

Коэффициент w f по существу задаёт функцию «штрафа» при удалении точки ( u’, v’ ) от эпиполярной линии au ‘ + bv ‘ + c , определяемой по координатам точки ( u 0 , v 0 ) с использованием фундаментальной матрицы F [12,13]:

a = u 0 F11 + u 0 F12 + F13, b = u 0 F21 + u 0 F22 + F23, c = u 0 F31 + u 0 F32 + F33.

На заключительном этапе с использованием полученных значений относительных сдвигов соответствующих точек на разноракурсных изображениях формируется карта диспарантности.

Наиболее ресурсоёмкими в описанной технологии являются этапы сопоставления фрагментов изображений с целью определения соответствующих точек на втором и четвёртом этапах технологии (рис. 1). Вместе с тем реализация именно этих этапов хорошо декомпозируется по данным. В частности, нахождение относительных сдвигов для каждой точки ( x, y ) можно выполнять независимо на отдельных процессорах. Для этого на каждом процессоре должна решаться задача минимизации критерия сходства (2). Реализация алгоритма на четвёртом этапе отличается лишь тем, что при вычислении на каждой нити критерия сходства E ( u, v ) добавляется также вычисление функции штрафа. Алгоритмы на обоих этапах успешно распараллеливаются. При этом количество нитей равно произведению числа пикселей изображения и числа всех возможных сдвигов ( u, v ) в области поиска D ₂.

Результаты экспериментов

При проведении экспериментов использовались стереоизображения из набора изображений «Tsukuba», которые часто используются в качестве тестовых в задаче сопоставления изображений. Этот выбор был продиктован тем, что указанная база изображений содержит также эталонные карты диспарантности, по которым возможно сопоставление результатов. Исходные изображения представлены на рис. 2.

С помощью предлагаемой технологии для указанных изображений была сформирована карта диспарантности (рис. 3а). На рис. 3б для сравнения приве- дена эталонная карта диспарантности, рассчитанная по тем же изображениям с использованием априорной информации о параметрах камер и хранящаяся в наборе изображений «Tsukuba».

а)

Рис. 2. Исходные изображения

б)

а)

б)

Рис. 3. Вычисленная (а) и эталонная (б) карты диспарантности

Для проверки технологии в случае, когда разноракурсные изображения зарегистрированы на большом расстоянии между камерами, была проведена следующая предварительная процедура. Исходные разноракурсные изображения из базы данных «Tsukuba» (рис. 2) были смещены в противоположные стороны. Таким способом были смоделированы изображения (рис. 4) с большим относительным пиксельным сдвигом. Фактический параллакс при этом не изменился, однако применяемое моделирование больших сдвигов адекватно воспроизводит эффекты, возникающие при большом расстоянии между камерами.

а)

Рис. 4. Смещённые изображения

При реализации алгоритма сопоставления точек на смещённых изображениях (рис. 4) получена карта диспарантности, которая демонстрирует большие ошибки сопоставления изображений (рис. 5 а ). Применение предварительного этапа совмещения к тем же смещённым изображениям позволило значительно сократить определение ложных относительных сдвигов (рис. 5 б ). Нетрудно заметить, что визуально карта диспарантности, показанная на рис. 5 б ) имеет большее сходство с эталонной (рис. 3 б ).

Для сравнительной оценки эффективности полученных карт диспарантности был предложен критерий качества K , который вычислялся по формуле:

m - i n - i

K(11,12) = — III11 (i, j) - 12(i, j)|, mn i=0 j=0

где I 1 – функции распределения яркости полученной карты диспарантности, а I ₂ – эталонной.

а)

б)

Рис. 5. Результат обработки «смещённых» изображений: а) без предварительного совмещения, б) с предварительным совмещением

Значение критерия качества для исходных изображений (рис. 3 а ) составило K = 7,36, а для смещённых (рис. 5 б ) K = 11,9. Очевидно, что без этапа предварительного совмещения карта диспарантности (рис. 5 а ) получается менее точной.

В табл. 1 приведены результаты сравнительных исследований времени реализации технологии на CPU и GPU при различном числе уровней пирамиды, задаваемых на первом этапе устранения больших относительных сдвигов (данные получены при реализации с использованием Geforce GTX 780 и Intel Core i7-4770K).

Табл. 1. Время реализаций в миллисекундах

Уровень пирамиды	1	2	3	4	5	6
Разрешение изображения	20×15	40×30	80×60	160×120	320×240	640×480
Размер в пикселях	300	1200	4800	19200	76800	307200
Время выполнения на CPU (мс)	9,4	42,8	185,3	753,1	2994,5	12081,9
Время выполнения на GPU (мс)	1,1	2,1	6,5	24,6	93,7	363,4
Ускорение	8,5	20,3	28,5	30,6	32	33,2

На рис. 6 приведены графики зависимости времени реализации технологии на CPU и GPU от размера обрабатываемого изображения.

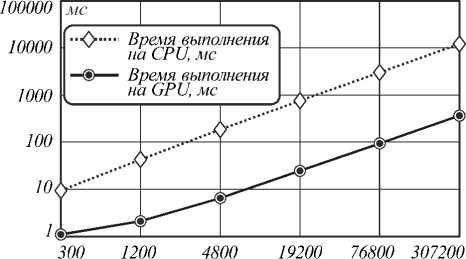
Рис. 6. Зависимость времени реализации на CPU и GPU от размеров изображения

Ниже приводятся также примеры, реализации разработанной технологии построения ЦММ, по данным ДЗЗ. В частности, использованы исходные тестовые изображения из того же набора, что и в работе [5]. В отличие от работы [5] использовались снимки той же местности под другим ракурсом с дополнительно введенным значительным смещени- б)

ем (рис. 7). Эти различия можно заметить по отбрасываемой тени от зданий.

Рис. 7. Смещённые снимки

На рис. 8 приведена карта диспарантности, полученная на смещённых разноракурсных изображениях при реализации технологии без этапа предварительного совмещения.

Рис. 8. Результат обработки «смещённых» снимков без предварительного совмещения

На рис. 9 приведена карта диспарантности, полученная с использованием предварительного этапа совмещения разноракурсных изображений. Приведённые изображения являются реальными аэрокосмическими снимками, на которых нельзя дать точные количественные оценки. Тем не менее, визуально заметно, что карта диспарантности, приведенная на рис. 9, в отличие от рис. 8 правдоподобна. Это подтвер- ждает, что предварительное совмещение разноракурсных изображений позволяет значительно уменьшить среднюю величину сдвига и, как следствие, сократить число ложных соответствий.

Рис. 9. Результат обработки «смещённых» снимков с предварительным совмещением

При сравнении этих изображений с приведёнными в работе [5] нетрудно заметить, что предложенная модификация технологии не снижает качество восстановления карты диспарантности, при этом позволяя обрабатывать снимки, полученные с больших ракурсов и с дополнительным смещением.

Заключение

Показано , что предложенная информационная технология сопоставления стереоизображений, основанная на использовании предварительного совмещения разноракурсных изображений и учёте эпиполярных ограничений обеспечивает достаточно высокое качество формирования трёхмерной модели сцены и цифровой модели местности. Сравнительные исследования времени построения карт диспарантности и восстановления 3D-сцен на CPU и на графических процессорах показывают увеличение быстродействия технологии в целом в 15 раз. Применение быстродействующего параллельного алгоритма в CUDA-среде вселяет надежду на возможность оперативной реализации технологии в реальном времени.

Работа выполнена при поддержке Российского научного фонда (РНФ), грант № 14-31-00014.