Технология оптимальной оценки направления линейной антенной решетки на источник сигнала при воздействии на нее коррелированных помех с неизвестной функцией распределения

При разработке современных гидроакустических систем дальнего обнаружения морских объектов и физических явлений значительное внимание уделяется методам обработки сигналов в эквидистантных линейных антенных решетках. Они представляют собой сенсорные системы, состоящие из размещенных на одинаковом расстоянии гидрофонов, предназначенных для интерпретации акустических волн. Обработку сигналов в указанных эквидистантных линейных решетках необходимо понимать как задачу оптимальной многоканальной фильтрации, основной целью которой является не только обнаружение полезного сигнала, но и оценка его параметров, несущих информацию о пространственном положении источника колебаний. При этом распространение сигнала происходит при наличии шума окружающей среды.

В связи с тем что многоэлементная антенная решетка в задачах гидролокации используется в основном для пространственной фильтрации или угловой селекции, многие работы по этим вопросам посвящены в основном методам получения требуемых диаграмм направленности с помощью весового суммирования сигналов отдельных элементов решетки. В основе такого подхода лежит предположение, что наилучшим способом, обеспечивающим большую эффективность обнаружения сигнала, является формирование некоторой диаграммы направленности решетки. Так как волна по определению есть функция пространства и времени, т.е. имеется функциональная зависимость между пространственной и временной переменными, то при более общем подходе к проблеме обнаружения сигнала и определения угловых характеристик его источника на форму диаграммы направленности не накладывается каких-либо ограничений. В этом случае технологии волновой обработки, включающие пространственное и временное измерения и основанные на методах пространственно-временной обработки сигналов, позволяют получить более значительное увеличение эффективности, чем при обычном подходе.

Основная часть

Обработка пространственно-временного сигнала обычно проводится в присутствии в гидроакустическом канале шумов и помех среды. Поэтому для таких условий надо говорить об оценке направления, т.е задача определения направления на источник уже относится к области статистической обработки. В таком случае для решения поставленной задачи необходимо предварительно задать статистические характеристики шума, определить критерии оптимальности и модель формирования пространственно-временного сигнала.

В традиционных методах оценки направления, как правило, предполагается, что функция распределения шума известна, шумы на гидрофонах не коррелированны и имеют одинаковую дисперсию. В реальной обстановке такие предположения выполняются редко. Например, помеха от точечного отражателя/излучателя формирует на решетке коррелированную помеху, в результате чего в гидрофонах помехи не только становятся коррелированными, но и имеют различную дисперсию [1]. В данной работе будем считать, что на интервале наблюдения шум (сюда входят и помехи) является стационарным процессом с нулевым средним, неизвестной функцией распределения, не обязательно белый. В качестве критерия оптимальности примем, что оценка должна быть несмещенной и с минимальной дисперсией.

Рассмотрим теперь модель пространственно-временного сигнала, формируемого линейной антенной решеткой.

В предположении плоского волнового фронта поле акустического давления формирует пространственно-временной сигнал, как показано на рис. 1.

Полагаем, что цель излучает/отражает гармонический сигнал вида

⁵ ( t ) - a- cos^ - f⁰¹ -^ ) ,                                                    (1)

где а - амплитуда сигнала; f - несущая частота; V - начальная фаза.

Считаем, что антенная решетка расположена в дальней зоне, когда волновой фронт сигнала плоский, как представлено на рис. 1. В таком случае сигнал на m -м гидрофоне запаздывает

d относительно (m - 1)-го на величину —sinф0, где d - расстояние между гидрофонами, c - ско-c рость звука в воде. Тогда на отдельном гидрофоне формируется информационный сигнал

I I d                     ।

5 ( m, t ) = a - cos I 2nf 0A t --sin ф ₀ - m 1- ^

= a - cos I 2.nf‘t - 2п I —sin ф I m -У I,

I 0       I A.      0 J J где λ0 – длина волны.

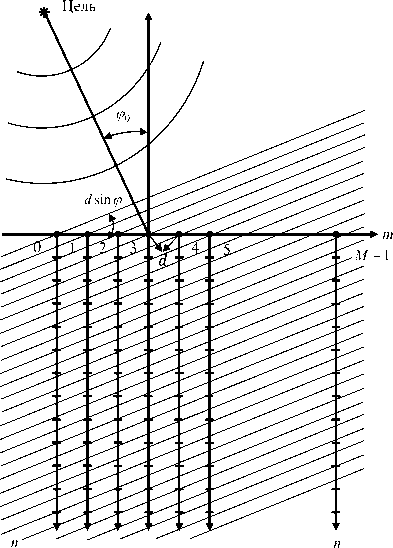
Рис. 1. Модель формирования пространственно-временного сигнала

После аналого-цифрового преобразования сигналов в каждом канале выражение (2) становится

I d 1^1 s(m, n) = a • cos I 2nf 0 n — 2п I —sin Ф0 I m -V I,

I                                                          J

\                   X v                      / fn'/ где n = 0 - N- 1 - номер отсчет в области времени; fj = °уд. ; fД - частота дискретизации.

В реальной обстановке информационный сигнал (3) приходит на антенную решетку в аддитивной смеси с шумом гидроакустического канала ω ( m , n ).

В результате на выходе гидрофона формируется сигнал

x ( m , n ) = s ( m , n ) + ω ( m , n ),

где ω ( m , n ) – шумовая составляющая, которая включает и помехи.

Перепишем выражение (4) в развернутом виде:

x

( m , n ) = a • cos I 2nf 0 n - 2 n

— sin ф₀ | m -Y

+ to (m, n ) =

= a • cos (2n f 0 n) • cos (2nS0 m -Y) + a • sin (2n f 0 n) • sin (2nS0 m -Y) + to (m, n), где

d

S o = —sin ф ₀.

Sergei V. Shostak, Paul A. Starodubtsev… Best Technology Assessment Areas Linear Array on the Source when Exposed… _

Раскрывая изменение сигнала во времени (по переменной n), получим x (m,0) = a • cos (2n J0 • 0) • cos (2nS0 m -V)+ a• sin (2nf 3 • 0)• sin (2я90 m - V)+ o( m ,0)

x ( m ,1) = a • cos (2 n f 0 • 1) • cos ( 2 я9 ₀ m -V )+ a • sin (2 n J 0 • 1) • sin (2я 9 ₀ m -V )+ o ( m ,1)

• •••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••••A*

-. (6)

x ^{( m} , N ^- 1)= a • cos ( 2^nf ₃ •( N ^- 1)⁾• cos Г - ^m-V ) +

+ a • sin (Ml 0 • ⁽ N ^{- 1))}• sin 12 -Д, ^{m -V )+ o ( m} , N ^- 1)

Выражение (6) несложно представить в векторно-матричной форме

где

X = H'-9' +W ^л m ^{AA v}m ⁺ ’’m ,

	x ( m ,0 )		_            1                        0
X m =	x ( m ,1 ) M	;             H ' =	cos ( 2 n f 0 • 1 )        sin ( 2 n f 0 • 1 ) MM
	[ x ( m , N - 1 ) _		_ cos ( 2 n f 0 ( N - 1 )) sin ( 2 n f 0 ( N - 1 ))

a • CoS ^{( 2 n} ^ 0 ^{m -V} ) = a COS (^{2 n} ^ 0 ^{m -V} ) ; a • sin ( 2 пЭ ₀ m -V )      sin ( 2 пУ ₀ m -V )

W

m

o ( m , 0 ) o ( m ,1 )

o ( m , N - 1 ) _

из соотношения (7) следует, что информацию об амплитуде сигнала a и направлении на источник ф 0 несет вектор 0m при искажающем воздействии шумового вектора W_m . Для получения последующих результатов представим пространственно-временной сигнал, сформированный антенной решеткой, в общем векторно-матричном виде, в результате чего образуются следующие выражения:

X 0

x ( 0, N - 1 ) x ( 1,0 )

X =

XM-1

x ( 1, N - 1 )

x ( M - 1,0 )

x (M -,1, N -3, MN^i cos (2nf 0 (N -1))

^{sin ( 2 n f} 1 ^{( N -} 1 ))

H =

0 LL

0          cos ( 2 n f _D ( N - 1 )) sin ( 2 n f _D ( N - 1 ))

cos ⁽ 2 n f 0 ⁽ N - 1 )) sin ⁽ 2 n f 0 ⁽ N - 1 )) .

MN x 2 M

0 =

⁰ M-i

M

2 M x 1

W =

W M-1

to (0,0)

® ( 0, N - 1 )

to . M - ^1, 4 - 13.

MN ^ i

Окончательно в компактном

виде модель пространственно-временного сигнала решетки можно записать таким образом:

где X – вектор измерений размерностью ( MN × 1); H – матрица связи размерностью ( MN × 2 M ); θ – вектор параметров размерностью (2 M × 1); W – вектор шума размерностью ( MN × 1).

В выражении (12) вектор X является вектором сигналов, измеренных на гидрофонах, H – известная матрица.

Из выражения (12) видно, что модель формирования сигнала в антенной решетке представляется в виде линейного векторно-матричного уравнения, где искомой величиной выступает вектор θ . Для оценки θ в подобного рода моделях применимы методы линейного оценивания, когда оценки вычисляются как линейные комбинации взвешенных с определенными весами, которые необходимо определить, наблюдаемых сигналов [2, 3]. К достоинствам таких оценок относится возможность получать несмещенные оценки, а также то, что они не требуют точного знания статистик шума, а только моменты до второго порядка включительно.

Обобщенный метод линейного оценивания основан на выражении

0 = A • X ,                                                                  (13)

где A – неизвестная матрица весов, которую требуется определить.

Как известно, основным требованием к методам оценивания является требование выделения насколько можно точнее некоторых величин из зашумленных данных [2, 3 ,4]. К такому требованию относится требование несмещенности оценки

E [ 6 ] = 0,                                                                             (14)

где E – оператор математического ожидания.

Из-за наличия шума при оценке θ снова формируется случайный процесс, и тогда метод линейного оценивания дает

е [ 6 ] = E [ AX ] = E [ A ( H0 + W )] = E [ AH0 • AW ] = AHE [ 0 ] + AE [ W ] = AH0 + AE [ W ] . (15)

Так как ранее было положено, что среднее значение шума равно нулю, т.е. E[W] = 0 , то матрица A должна удовлетворять условию

A ∙ H = I ,                                                                  (16)

где I – единичная матрица.

Получим теперь выражение для дисперсии вектора оценки θˆ через ковариационную матрицу еГ(6 - 0)(0 - 0)T

= e [ ( AX - 0 )( AX - 0 ) ^T ] = e [ ( AH0 + AW - 0 )( AH0 - AW - 0 ) ^T ] , (17)

где Т – операция транспортирования.

С учетом условий (16) получим

E r ( e — _e ⁾⁽ 0 — 0 ^{) T}

= e [ ( AW )( AW ) ^t ] = e [ aWW ^t A T ] = Ae [ wW ^t ] a ^t = AC_WA ^T,

(17а)

где C W – ковариационная матрица шума.

Кроме требования несмещенности, другим требованием к оценке служит оценивание с минимальной дисперсией. Для этого необходимо найти матрицу весовых коэффициентов A , которая давала бы минимальное значение (17) с учетом условий (16). Эта задача на поиск условного минимума и решение ее получено в [2-4] на основе теоремы Гаусса-Маркова, из которой следует, что если данные измерений есть общая линейная модель вида

X = H ■ 0 + W , (18)

где H – известная ( MN × 2 M ) матрица, θ есть (2 M × 1) вектор параметров для оценивания, W есть ( MN × 1) произвольно распределенный шумовой вектор с нулевым средним и известной ( MN × MN ) ковариационной матрицей C W , то наилучшей линейной несмещенной оценкой для θ ^ˆ является

0 H CWH1 HTCW X.(19)

TTA

При этом дисперсия оценки θ определяется выражением var (0 )=(H TCW H)-1,(20)

а минимальная дисперсия оценки отдельного параметра Ут varfe. )=[(H T C—1H Г1 ] mm.

Для нашего случая получили, что

A-(HTCWW H) HTCW.

В частном случае, если W белый шум с ковариационной матрицей

где °w - дисперсия шума, то Cw = — • I, и тогда выражение оценки (19) приобретает вид °W e = (htc-1h)-1

• H T C - 1 X = II ¹ 1 I H

I    ° W .

• H T

> I

• X = ( H ^{T H} ) ^{- 1} • H T X , (24)

т.е. сводится к стандартной процедуре наименьших квадратов.

- I

Множитель С_W в (19) проводит предварительное предотбеливание данных до усреднения, т.е. выравнивает шумовой вклад каждого гидрофона. Тогда, если W имеет гауссовское распределение, то в результате вектор θ также будет распределен по нормальному закону с ковариационной матрицей вида (22).

Как показывает (10), вектор θ состоит из ряда косинусов и синусов, искаженных шумом, который приведен к белому. Последовательности косинусов и синусов в θ являются функция- d ми, где в качестве аргумента выступает номер гидрофона, а постоянная величина 50 = — sin ф0

имеет смысл пространственной частоты, т.е.

sin ( 2 ⁿ^ 0 m ^-y ) = sin 2 ⁿ _; sin Ф о I m ^-y .

В результате задача оценки направления на источник сводится к оценке пространственной частоты ϑ0 гармонического колебания на фоне белого шума с минимальной дисперси ей.

Вектор оценок параметров (19) с помощью ( M × 2 M ) матрицы

D =

1 j 0 0 L 0 001 j L 0

0 LLL 1 j

M x2 M где j = -i 1 - мнимая единица, несложно преобразовать в комплексный вид

Z = D • 0 .

Далее вектор Z легко представить в виде комплексного сигнала переменной m :

j l 2л \ —sin ф о I m ^{- y}

В работе [5] проведено решение задачи оценки амплитуды, частоты и начальной фазы гармонического сигнала вида (28) на фоне белого гауссовского шума методом максимального правдоподобия. Представленные результаты показывают, что наилучшим методом оценки частоты является метод периодограммы [5, 6], который для нашего случая имеет вид

M

M - 1

m = 0

где – абсолютное значение (модуль) выражения.

Подставим в (29) информационную часть (28):

-V ) ■ exp ( - j 2 n9 m )] =

M

m_ — 1       r .

E a ■ exp [ j (2nf0 m m=0

—

M

a ²

M

M - 1

m = 0

M_ - 1

E exp m=0

j S ^--sin ^ф y^m

Несложно заметить, что в случае 9 = 9 ₀ = — • sin ф ₀ (30) имеет максимальное значение.

Следовательно, оценка пространственной частоты S ₀ и угла □ 0 соответственно определяется выбором частоты ϑ , для которой периодограмма достигает максимального значения. При этом неравенство Рао-Крамера дисперсии оценки 9 ₀ имеет вид [2, 5]

var 9 ) .

a ■ M

I M ^ ^r a ^TT- ам и [ „ | j M ^{( м - 1)}

a ²

где q = —2 - отношение сигнал/шум. о_Е

Выражение (31) показывает, что граница Рао-Крамера оценки пространственной частоты обратно пропорциональна отношению сигнал/шум и уменьшается обратно пропорционально третьей степени числа гидрофонов в линейной антенной решетке, что делает рассмотренный способ достаточно помехоустойчивым.

тт

По предложенной технологии оценки направления на источник излучения несложно сформулировать алгоритм обработки сигналов, который содержит совокупность следующих методов и инструментов:

• 1)    оценка автокорреляционной матрицы помех C_W ;

• 2)    формирование вектора входных сигналов в соответствии с (8);

• 3)    формирование матрицы H в соответствии с (9);

• 4)    получение матрицы A в соответствии с (22);

• 5)    вычисление θ ˆ в соответствии с (13);

• 6)    формирование матрица D в соответствии с (26);

• 7)    определение Z в соответствии с (27);

• 8)    вычисление периодограммы (29);

• 9)    нормирование частотной оси периодограммы в угловых единицах.

Заключение

Таким образом, в настоящей работе получена технология оптимальной оценки направления на источник сигнала для линейной антенной решетки при воздействии на нее некоррелированных помех с неизвестной функцией распределения. При этом предполагается, что плотность вероятности щума неизвестна, но он может быть описан первым и вторым моментами. Сформированный антенной решеткой пространственно-временной сигнал описан в виде линейной модели (7), которая включает и шумовую составляющую. В рамках данной модели (10) представляет собой вектор параметров, который несет информацию о направлении и который необходимо предварительно оценить.

Требования несмещенности и минимума дисперсии оценки реализованы на основе теоремы Гаусса-Маркова в виде матрицы весовых коэффициентов, которыми взвешиваются сигналы на выходе отдельных гидрофонов, в результате чего «отбеливается» шумовая составляющая пространственно-временного сигнала и минимизируется ее дисперсия.

Оценка (13) с помощью матрицы (26) легко преобразуется в дискретную экспоненту (28), у которой пространственная частота определяется направлением на источник отражения/излу-чения. Тем самым задача оценки направления свелась к задаче оценки частоты гармонического сигнала в «белом» шуме. Анализ решения такой задачи методом максимального правдоподобия показал, что наиболее удобным и реализуемым является метод на основе периодограммы (29), (30).

Необходимо также отметить важное свойство оценки частоты гармонического сигнала: из неравенства Рао-Крамера следует, что дисперсия такой оценки обратно пропорциональна третьей степени числа гидрофонов и обратно пропорциональна отношению сигнал/шум (31). Поэтому изложенная в настоящей статье технология основана на линейной модели представления пространственно-временного сигнала, удовлетворяющей условиям несмещенности и минимума дисперсии оценок, включающей периодограмму для оценки частоты.

Данная технология легко реализуема в современных гидроакустических системах дальнего обнаружения морских объектов и физических явлений и, следовательно, привлекательна для практического применения.