Технология оптимизации энергосбережения в гибридной ветро–солнечной системе накопления энергии

В последние годы в литературе усилилось внимание к методам оптимального управления гибридными источниками и виртуальными электростанциями, где важно учитывать неопределённости и отзывчивые нагрузки — так, в работе [1] показан риск-ориентированный подход к оптимизации управления виртуальной ветряной электростанции, что обосновывает использование адаптивных алгоритмов оптимизации. Параллельно исследования по управлению ветровыми установками с батарейным накоплением [2], [3] демонстрируют эффективность координации источников и накопителей для сглаживания выработки и обеспечения надёжности при переменных режимах работы.

Важную роль в повышении быстродействия и продлении ресурса батарей в гибридных системах занимают комбинированные схемы хранения: обзор [4] даёт общее представление о типах гибридных систем накопления энергии и их достоинствах/ ограничениях. Из–за нестабильности и непредсказуемости, мощность гибридной ветро-солнечной системы накопления энергии может изменяться случайным образом и с перерывами. По сравнению с традиционными источниками энергии, такими как атомные и угольные тепловые электростанции, возобновляемые источники энергии могут быть труднодоступными для использования в сети [5]. Учитывая, что выходная мощность ветро-солнечной гибридной системы накопления энергии должна достигать идеально стабильного уровня, необходимо внедрить диспетчеризуемое накопление энергии.

Отдельно следует отметить проблему управления реактивной мощностью и координации компенсирующих устройств: авторы работы [6] демонстрируют успешное применение PSO для согласования SVC/TCSC при управлении потоками мощности, что служит опорой для выбора PSO/алгоритмов роя в задачах статической компенсации. В то же время по совмещению всех элементов — ветро-PV генерации, двухуровневой гибридной системы накопления энергии (суперконденсаторы + батареи), адаптивных MPPT/PSO-алгоритмов и систем статической компенсации — в одном интегрированном решении и особенно с фокусом на суровые (арктические) условия в доступной литературе наблюдается пробел. Настоящая работа направлена именно на заполнение этой ниши.

В кандидатской диссертации Абдали Л. М. [7] представлена детальная разработка системы управления и алгоритма повышения эффективности гибридных ветро-солнечных электростанций с фокусом на моделирование режимов генерации и оптимизацию работы основных элементов. В отличие от этого, настоящая работа расширяет область исследования за счёт интеграции двухуровневой системы накопления энергии (суперконденсаторы + аккумуляторы), включения механизмов статической компенсации реактивной мощности (SVC/STATCOM) и применения комбинированной стратегии управления, объединяющей MPPT для PV, адаптивные регуляторы и алгоритм оптимизации роя частиц (PSO) совместно с VSS-ПРМ для быстрого перехода между режимами. Кроме того, в работе уделено внимание влиянию низких температур и эксплуатационным условиям Крайнего Севера, а также практическим аспектам реализации (техническая спецификация, требования к обогреву и обслуживанию). Такое сочетание быстродействующих накопителей, средств поддержания качества напряжения и адаптивных алгоритмов управления направлено на решение задач, не полностью охваченных в ранее выполненной диссертации, и обеспечивает большую прикладную ценность для внедрения в отдалённых и арктических регионах.

В данном исследовании объединены конденсатор и аккумулятор в единую систему накопления энергии. Как по энергетической емкости, так и по продолжительности цикла заряда–разряда эта технология превосходит отдельные конденсаторы и акку- муляторные батареи. Рассматривается процесс улучшения эффективности гибридной ветро-солнечной системы хранения энергии, использующей комбинацию конденсаторов и аккумуляторов для накопления энергии. Для повышения производительности системы применяются методы, такие как оптимизация с использованием алгоритма потока частиц (ОПЧ) и система слежения за максимальной мощностью (ОТММ). Система, подключённая к сети, эффективно сочетает ветер и солнечную энергию благодаря их взаимодополняемости. Важное улучшение в управлении энергией достигается благодаря двухрежимному алгоритму, который также упрощает распределение мощностей. Это решение не только снижает затраты на хранение энергии, но и повышает как экологическую, так и экономическую целесообразность.

Таким образом, основной целью работы является анализ и оптимизация гибридной ветро–солнечной системы накопления энергии с целью повышения ее эффективности, увеличения емкости накопителя и выходной мощности за счет применения методов двухрежимного управления и статической компенсации реактивной мощности, а также оптимизация системы с использованием программного моделирования в MATLAB/Simulink.

Материалы и методы

В данном разделе описана конструкция гибридной системы, предназначенной для накопления энергии, которая функционирует на основе ветровой и солнечной генерации. Рассматриваются математические модели для основных элементов системы, таких как солнечные панели (ФЭМ), ветрогенераторы, конденсаторы, инверторы и преобразователи мощности.

Модель фотоэлектрического модуля (ФЭМ).

На схеме (рис. 1) показана гибридная система накопления энергии, работающая на ветровой и солнечной энергии. В состав системы включены ветрогенераторы, инверторы, шины постоянного и переменного тока, солнечная панель и устройство накопления энергии. В распределённой системе генерации электроэнергия сначала поступает на шину постоянного тока, а затем преобразуется в переменный ток с использованием инвертора. Система накопления управляет распределением энергии, обеспечивая стабильное электроснабжение как потребителей, так и сетей [8].

Шина постоянного тока

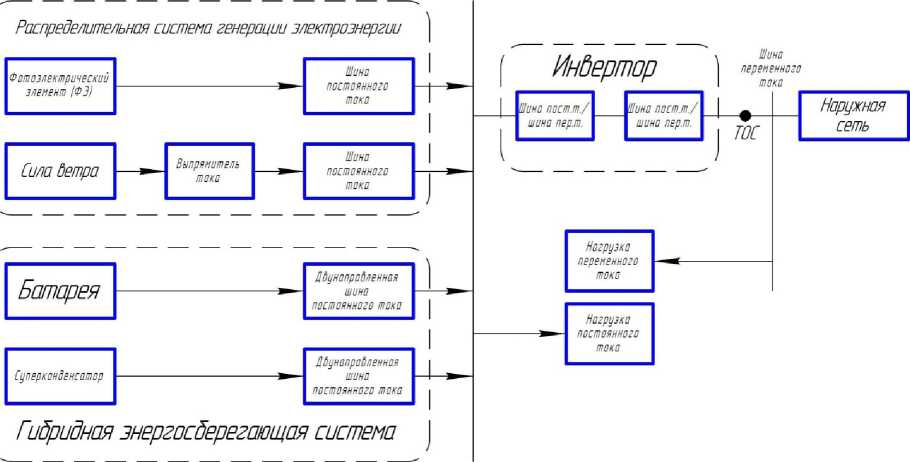
Рисунок 1. Схема подключенной к сети гибридной системы накопления энергии ветра и солнца

Фотоэлемент является самым базовым элементом солнечной энергетической системы. Соотношение выходной мощности между фотоэлектрическими элементами составляет:

г              ч ( Г V+,R^1

P = IV = (Jph -Id- ISJ • v = [lpn - /0      -1]^]V

• r         V+1R_S v + IR^

• - \lph~ ^Oe A “ ^0 n '

где I – выходной ток;

I_d – ток диода в этой эквивалентной схеме;

I_ph – ток, генерируемый фотоэлектрической решеткой;

I_sh – ток, протекающий по параллельному сопротивлению;

A – идеальный коэффициент для P – N перехода (полупроводники – P –тип (positive) и N –тип (negative));

V – напряжение на клеммах нагрузки;

R_s – последовательное сопротивление.

Эту формулу можно упростить в виде следующей формулы, поскольку Rsh бесконечно велико, а Rs бесконечно мало:

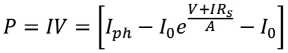
V

Математическая модель для ветряных турбин.

Для оценки плотности вероятности данных о скорости ветра воспользуемся распределением Вейбулла. Формула представлена следующим образом:

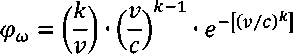
Функция распределения плотности вероятности получается путем интегрирования данной функции:

фы — 1 — e l^/^, (/с > 0, с > 1)

В предыдущей формуле k определяет форму кривой. c – параметр масштабирования, и c обычно считается средней скоростью ветра.

Для определения значения перемотки выходной мощности выполняется расчет линейной интерполяции по формуле, представленной авторами в источнике [5]:

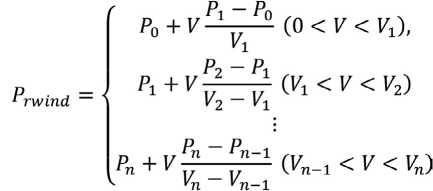
Математическая модель для суперконденсаторов.

В работе [5] показано, что ёмкостные значения и напряжения соответствуют обеим сторонам конденсатора, а AW представляет собой изменение энергии суперконденсатора в эквивалентной схеме ( AW представляет собой интеграцию PC(t) с t) в интервале [t(n-1),t(n + 1)] . Изменение энергии конденсатора происходит следующим образом:

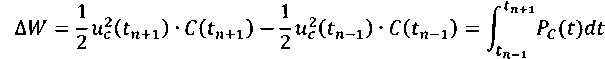
где uc(t) – напряжение на конденсаторе

R_s – последовательное сопротивление конденсатора

C(t) – измеренное значение для конденсатора us(t) – напряжение на последовательном сопротивлении.

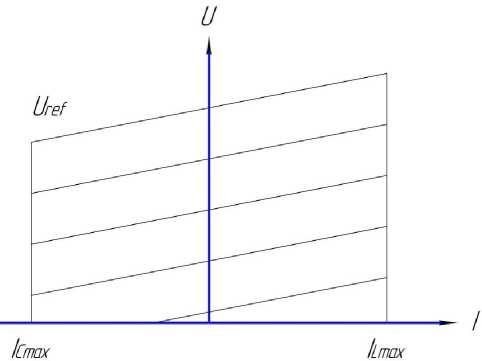
Рисунок 2. Вольт-амперные характеристики СВГ

Согласно рис. 2, мгновенная мощность конденсатора выражается общей мгновенной мощностью и мгновенной мощностью сопротивления [9]:

P c (t) = u(t) • i(t) - i²(t) • R s

Математическая модель выходной мощности инверторов.

Питание нагрузки в основном поступает от инвертированной батареи. Выходная мощность инвертора равна P_out , а входная – P_in . Таким образом, коэффициент полезного действия η рассчитывается как:

Входная мощность равна сумме выходной мощности и потерянной мощности, что следует из источника [10]:

P _in = P _out + P _loss = p ₀ + kp²

Тогда получим:

p        _d Po + kp²

T] = ---------- =1-- p + p0 + kp2 p + p0 + kp2

В предыдущей формуле p = P_ou/P_in ( p — инвертор, a P_in - номинальная мощность инвертора); уравнение выражения для P₀ с k имеет вид:

_ 9 / 10      1      \2

11 \9?]₁₀ 9р₁₀₀    /

КПД инвертора при напряжении 10 % равен η10 , а КПД инвертора при напряжении 100 % равен η100 .Эти характеристики приведены в следующем уравнении:

к =-- р₀ - 1 Рюо

Математическая модель преобразователей.

Преобразователи способны конвертировать мощность из шины переменного тока в шину постоянного тока. Двунаправленный преобразователь можно представить системой уравнений, как предлагаю авторы [5]:

Pinv Pinv        Peon,DC > Pinv

Peon,DC ' ^inv 0 <  Peon,DC < Pinv

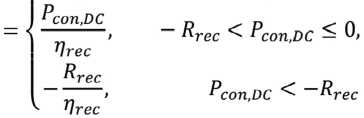
где P_conAC – питание на стороне переменного тока. Положительное значение указывает на и ^, нвертирование, а отрицательное – на выпрямление;

P_conDC – общая мощность на стороне постоянного тока;

R_rec^, – максимальная мощность, когда инвертор находится в режиме выпрямления.

Система хранения энергии ветра и солнца, подключенная к сети.

Стационарный компенсатор реактивности позволяет точно контролировать стабильность электросети, улучшает управляемость и обеспечивает быстрое реагирование. Согласно теории реактивной мощности, блок статического генератора переменного тока и сеть не имеют потерь при обмене энергией; тогда общая мгновенная мощность сети фиксирована и не приводит к потерям энергии в компенсаторе [11].

Мощность статического компенсатора определяется изменением напряжения на шине. Используется метод расчета расхода электроэнергии. Чтобы гарантировать, что мощность системы составляет 1 ≥ cosφ ≈ ≥ 97,0 %, необходимо добавить параллельные конденсаторы в качестве компенсации, тогда коэффициент мощности системы показан ниже:

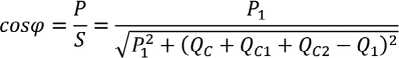
где S – мощность ветроэлектростанции;

Q_C2 – источник реактивной мощности;

Q_C1 – мощность емкостной зарядки линии;

P₁ и Q₁ , соответственно, указывают активную и реактивную мощность ветроэлектростанции до компенсации.

Стратегия управления статическим варьируемым генератором (СВГ).

В соответствии с математической моделью СВГ, для отслеживания максимальной мощности (ОТММ) был создан контроллер с двойной системой обратной связи, а для регулирования напряжения внешней цепи применяется ПИ-регулятор (пропорционально-интегральный).

Входными значениями являются команда напряжения на стороне постоянного тока U_C * и команда напряжения в точке общего соединения (ТОС) U_PCC *, которые генерируют опорные сигналы для текущего внутреннего контура. На рис. 3 два опорных сигнала соответствуют двум напряжениям на внешнем кольце и линейному активному регулятору подавления помех (ЛАРПП) на внутреннем кольце. На выходе устройства подается импульсный сигнал напряжения [12].

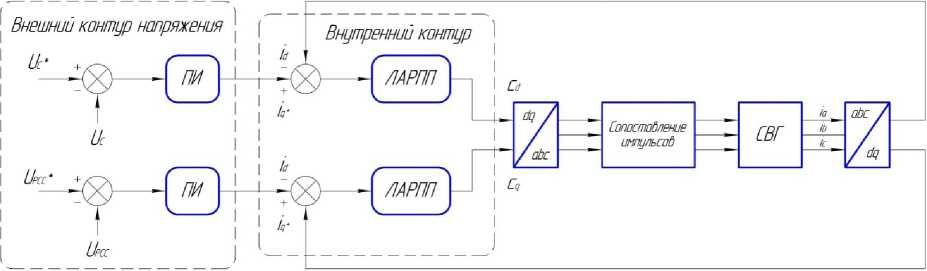
Рисунок 3. Схема двойной замкнутой системы управления СВГ

Для обеспечения стабильности значения напряжения необходимо добавить систему управления по замкнутому контуру, чтобы достичь заданного значения напряжения на шине и коэффициента мощности системы ≥0,95 [13].

Улучшенная ОТММ–оптимизация метода двухрежимного управления.

Традиционный метод увеличения проводимости основывается на характеристиках самого фотоэлектрического элемента, который сохраняет стабильность даже при внешних изменениях, а колебания после достижения устойчивого состояния остаются минимальными. Для оценки, работает ли фотоэлектрическая панель на максимальной эффективности, используется её характеристическая кривая [6].

В соответствии с источником [5] алгоритм оптимизации потока частиц работает следующим образом: рассмотрим K–мерное пространство поиска, в котором количество частиц равно n , а положение и скорость частицы под номером i равны xi = (x1ⁱ, x2ⁱ,…, xkⁱ), V_i = (V1ⁱ, V2ⁱ,…, Vkⁱ) . Затем скорость и положение частиц обновляются, как показано на рис. 4.

, j_i ;           Pk ~ xk           Pk ~ xk vk+1 = pvk + v-prend——--1- v2rend——— vi + l _ I „i+1 xk ~ xk vk где pik – оптимальное положение i–й частицы в момент времени;

• p^g_k – оптимальное положение группы частиц k;

• ρ – коэффициент инерции;

• v₁ – локальный параметр надежности;

• v₂ – параметр надежности группы частиц.

Усовершенствованный метод увеличения проводимости, основанный на алгоритме оптимизации потока частиц, изменяет размер шага метода увеличения проводимости в соответствии с учетом расстояния между частицами и его порогового показателя, а это, в свою очередь, дает возможность отследить максимальную выходную мощность системы.

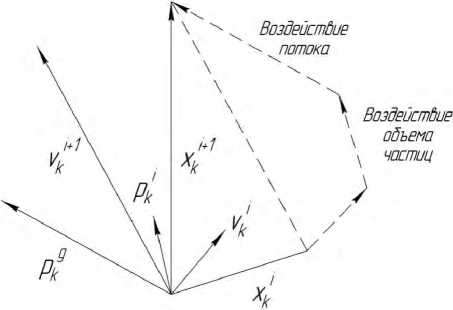
Рисунок 4. Изменение скорости и положения ОПЧ

Алгоритм нечеткого управления.

Нечетким управлением называют контроллер, разработанный исходя из опыта пользователя, не требующий создания собственной отдельной математической модели.

Принцип работы с потоком заключается в определении функции принадлежности контроллера и правил управления путем ввода номера и характеристик пользователя, а затем выбора подходящей функции. Управление завершается, как показано на рис. 5.

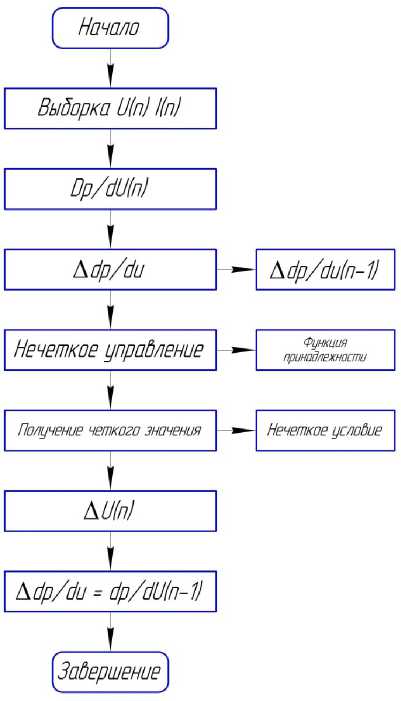
Рисунок 5. Схема метода нечеткого управления ОТММ

Учитывая, что метод нечеткого управления не требует специальной математической модели, отказоустойчивость может быть очень высокой. Однако нечеткая обработка информации приводит к снижению точности управления системой и динамического качества [14].

Результаты

Для проверки эффективности предложенной стратегии управления было проведено моделирование системы с возрастающей нагрузкой в сети, использующей ветро-солнечную энергогенерацию. Для моделирования системы в исследовании использовался инструмент MATLAB/Simulink. Параметры солнечной панели и схемы наддувочного устройства задаются следующим образом: интенсивность солнечного излучения на панели изменяется от 1000 Вт/м2 до 600 Вт/м2, а затем повышается до 800 Вт/м2; скорость ветра варьируется от 8 м/с до 10 м/с и затем снова снижается до 8 м/с. Входные и выходные ёмкости схемы составляют 500 мкФ, индуктивность – 5 мГн, а нагрузка – 25 Ом.

Рис. 6 показывает, что при скорости ветра 8 м/с и начальном освещении 1000 Вт/м2 оптимизированная гибридная система отражает максимальные показатели выходной мощности, за 0,16 с достигая стабильного состояния.

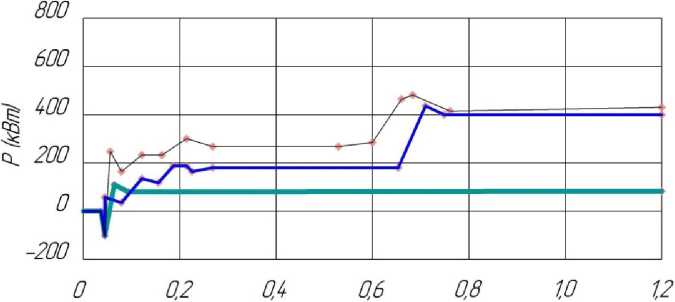
---------- Гибридная бетро-солнечная система, подключенная к сети ^^^^— Отдельная фотоэлектрическая система --------- Отдельная Ветробоя система

Рисунок 6. Сравнение выходной мощности отдельных систем выработки электроэнергии с подключенными к сети ветроэнергетическими системами

Переход фотоэлектрической системы в устойчивое состояние занимает около 0,05 с. В традиционной ветроэнергетической системе на это требуется примерно 0,115 с, при этом погрешность отслеживания в этой системе составляет около 0,23 %, а в двух других системах она в 1–2 раза выше. На этом этапе выходная мощность ветро-солнечной системы демонстрирует более долгий период устойчивого состояния с меньшими колебаниями кривой. Через 0,3 с скорость ветра увеличивается с 8 м/с до 10 м/с, при этом колебания кривых выходной мощности двух систем оказываются неравномерными [14].

Оптимизированной системе, дополняющей ветро-солнечную систему, требуется приблизительно 0,073 с, чтобы снова достичь устойчивого состояния. После оптимизации время, необходимое для достижения стационарного состояния ветро-солнечной системы, составляет приблизительно 0,05 с. Продолжительность составляет приблизительно 0,089 с, а погрешность отслеживания на 400 % выше, чем у оптимизированной ветро-солнечной системы [9].

Колебания кривых выходной мощности у них различны. За одну секунду интенсивность окружающего освещения увеличивается с 600 Вт/м2 до 800 Вт/м2, скорость ветра снижается с 10 м/с до 8 м/с, а время, необходимое для достижения устойчивой работы ветро-солнечной системы, оптимизируется с помощью обычных фотоэлектрических систем управления. В ходе процесса отслеживания, по мере улучшения оптимизации, кривая выходной мощности ветро-солнечной системы постепенно приобретает более плавный характер, что составляет половину времени по сравнению с традиционной ветровой системой управления и треть времени, необходимого для фотоэлектрической системы.

Дополнительная система показывает увеличение среднего времени отслеживания на 90 % по сравнению с двумя другими системами, использующими ту же энергетическую базу. Таким образом, оптимизированная производительность дополнительной ветро-солнечной системы выше [8].

Обсуждение

В данной статье проведена оптимизация гибридной ветро-солнечной системы накопления энергии путем пошагового усовершенствования емкостных характеристик структуры суперконденсатора. Система компенсации статического ветра и метод двухрежимного управления с нечеткой проводимостью применяются для оптимизации емкости. На основе MATLAB рассчитана и проанализирована модель оптимальной конфигурации гибридной системы накопления энергии.

Внедрение устройства статической компенсации для ветряных электростанций способствует стабилизации напряжения и снижает влияние колебаний мощности на напряжение в энергосети. Моделирование в среде MATLAB/Simulink показало, что при изменении скорости ветра мощность системы достигает стабильных и более быстрых колебаний.

Алгоритмы увеличения проводимости с оптимизацией группы частиц, двухрежимное управление с нечёткой проводимостью и традиционное нечёткое управление были смоделированы и проверены при различных уровнях освещенности. Результаты показывают, что двухрежимный алгоритм управления обеспечивает более быстрый переход к устойчивому состоянию с высокой точностью. Кроме того, он способствует увеличению времени автономной работы и снижению энергозатрат.

Оптимальные условия электроснабжения при интеграции различных энергоисточников достигаются путем синтеза ветро-солнечной и гибридной энергетических систем. Гибридные системы хранения энергии в будущем потребуют дополнительной оптимизации с помощью контроля уровня заряда суперконденсаторов и батарей.

Комбинация суперконденсаторов и аккумуляторов увеличивает ёмкость и скорость отклика системы, что снижает пиковую нагрузку и продлевает ресурс батарей — это важно для объектов Крайнего Севера.

Статическая компенсация реактивной мощности (SVC/статком) улучшает качество напряжения и стабилизирует слабые локальные сети, что критично для районов с малыми сетями (пример: отдалённые посёлки и промплощадки Ямала). Моделирование подтвердило сокращение времени установления устойчивого режима и уменьшение колебаний выходной мощности — это повышает автономность станций в таких пунктах, как радиометеорологические центры Тикси и Диксон. Технология целесообразна для пилотных внедрений на добычных площадках, береговых базах и отдалённых населённых пунктах (например, базы Ямала, порты Мурманской области) с целью снижения расхода дизельного топлива и повышения надёжности энергоснабжения.

В качестве направлений дальнейших исследований целесообразно организовать стендовые и пилотные испытания в условиях, приближённых к арктическим, чтобы получить эмпирические данные для калибровки моделей и оценки эксплуатационной надежности. Параллельно выгодно развивать адаптивные методы управления с он-лайн-обучением, гибридизуя эвристические алгоритмы (PSO) с методами машинного обучения, — это позволит повысить адаптивность системы без ручной перенастройки. Необходимо также углубить экономический анализ (CAPEX/OPEX, LCOE) и разработать методики техобслуживания и логистики для удалённых объектов, поскольку экономическая и операционная составляющие определяют реальную возможность внедрения решений на практике. Дополнительные исследования по термоконструктивной защите, методам противообледенения и стандартизованным процедурам тестирования HESS при экстремальных температурах обеспечат воспроизводимость испытаний и простоту сертификации.

Выводы

Оптимизированная гибридная ветро-солнечная система накопления энергии способствует стабилизации напряжения и снижает влияние колебаний мощности на напряжение в энергосети, а двухрежимный алгоритм управления способствует увеличению времени автономной работы и снижению энергозатрат. Результаты моделирования показывают некоторое увеличение выходных характеристик, что дает положительную оценку исследования и указывает на достижение поставленной цели.

Как и предполагалось, комбинация суперконденсаторов и аккумуляторов увеличивает ёмкость и скорость отклика системы, что снижает пиковую нагрузку и продлевает ресурс батарей.

Приведённая в данном исследовании модель целесообразна для пилотных внедрений на добычных площадках, береговых базах и отдалённых населённых пунктах (например, базы Ямала, порты Мурманской области и т.д.) с целью снижения расхода дизельного топлива и повышения надёжности энергоснабжения. Однако, моделирование проводилось на базе программного комплекса MATLAB/Simulink с заданными критериями, которые, к сожалению, не всегда соответствуют реальной картине внешних факторов того или иного субъекта Российской Федерации и очень сильно зависят от ряда других факторов, не учтённых при моделировании (например, разные параметры солнечного излучения в разные времена года). Таким образом, при исследовании произведено допущение, что параметры внешних факторов сохраняются на протяжении всего календарного года. Для более точного исследования требуется создание инженерных решений.

В целом, дальнейшая работа должна быть направлена на превращение моделируемых преимуществ гибридных систем в проверенные инженерные решения: это требует комплексного подхода — от уточнения физики элементов и силовой техники до испытаний в полевых условиях и экономической оценки, что в совокупности позволит обеспечить надёжное и эффективное независимое энергоснабжение в отдалённых и арктических регионах.

Также одним из направлений дальнейших исследований встает дополнительная оптимизация гибридной системы хранения энергии с помощью контроля уровня заряда суперконденсаторов и батарей.