Технология проектирования робастных баз знаний: сравнение управления нечетких регуляторов на разных типах регуляторов с помощью инструментария оптимизатора баз знаний

Известно, что при исследовании процессов управления сложных и слабоструктурированных динамических систем в условиях неопределенности, применение методов, базирующихся на использовании точных математических моделей, не позволяет построить адекватные модели и алгоритмы, позволяющих достигнуть оптимального управления. В последнее время, с увеличением сложности задач управления, все большее распространение получают технологии интеллектуального управления. Одним из важнейших направлений в теории интеллектуального управления в течение последних десятилетий является поиск решения проблемы оптимального управления сложными техническими системами в условиях неопределенности и возникновения дефицита или ограниченного полезного ресурса. Одним из самых эффективных методов решения задач в таких условиях является синтез системы с переменной структурой на скользящих режимах (СР).

Исследования в области СР являются одними из наиболее актуальных в настоящее время. Задача синтеза в системах с разрывными управлениями обычно сводится к построению поверхностей переключений в фазовом пространстве, на которых функции управления претерпевают разрывы. При выполнении определенных соотношений, в таких системах на данных поверхностях может возникнуть специфический вид движения – скользящий режим. Подобрать оптимальную структуру поверхности переключения управления является нелегкой задачей, даже для опытного эксперта. Для решения данных проблем были использованы технологии интеллектуальных вычислений, включающих мягкие вычисления с использованием ряда важных термодинамических, информационноэнтропийных и динамических критериев управления [1].

На практике часто для решения подобных задач используется нечеткий регулятор (НР), управляющий коэффициентами усиления ПИД-регулятора. НР осуществляет управление за счет интегрированной в него базы знаний (БЗ), включающей данные о виде и параметрах функций принадлежности входных и выходных нечетких переменных, а также набор нечетких продукционных правил.

Целью данной работы является сравнение качества управления НР на двух разных типах управления с помощью Оптимизатора баз знаний (ОБЗ).

Система со СР управления

Динамическое поведение нечеткого регулятора характеризуется множеством лингвистических правил, составленных экспертом. Пользуясь этим множеством, механизм нечеткого вывода выдает соответствующее управляющие воздействие [2]. Для двухмерного случая нечеткое управление может использовать: ошибку e и скорость изменения ошибки e в виде входных лингвистических переменных нечеткого правила. Таблица нечётких правил приведена ниже [3].

Таблица 1. Нечеткие правила

Аи	е
	NB      NM     NS      Z       PS      PM      РВ
РВ РМ PS ё       г NS NM NB	Z NZ NS NM NB NB NB PZ Z NZ NS NM NB NB PS PZ Z NZ NS NM NB PM PS PZ Z NZ NS NM РВ PM PS PZ Z NZ NS РВ РВ PM PS PZ Z NZ РВ РВ РВ PM PS PZ Z

Другой способ рассмотрения правил таблицы – это фазовая траектория, показанная на рис. 1, стрелки показывают направление усиления.

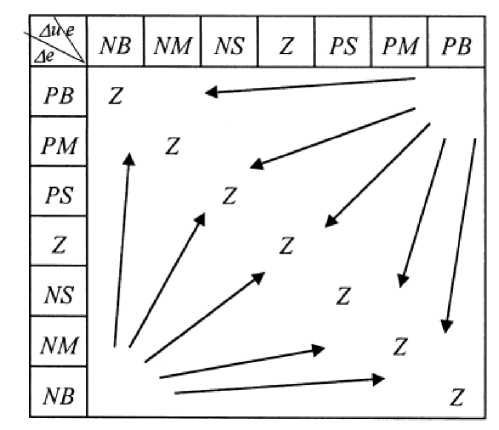
Рис. 1. Фазовая траектория НР

На рис. 1 Z - поверхность переключения. Из табл. 1 можно заключить, что если e и e близки к поверхности, то нечеткое управляющие воздействие сильное, чем дальше оно от поверхности, тем оно слабее. Поэтому, поверхность скольжения принимает вид: s = e + e (где w - положительная переменная и определяет скорость сходимости для e и e ).

Структура интеллектуальной системы управления(ИСУ) со скользя-щим режимом

На рис. 2 показана структура ИСУ для регулятора со СР. На вход блока вычислений s и s ' подается текущая ошибка управления (вычисляется как разность состояния ОУ и задающего сигнала) и скорость ошибки управления, после этого полученные значения поступают на вход НР, который выдает управляющее воздействие на ОУ [4].

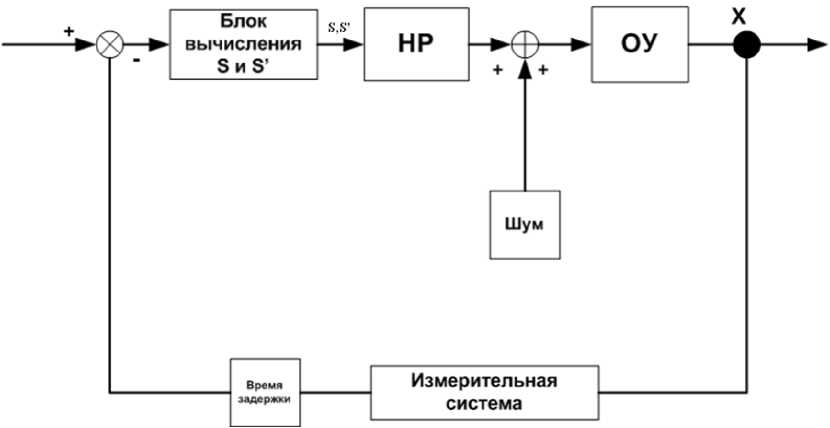
Рис. 2. Схема ИСУ

Структура ИСУ с ПИД -регулятором

На рис. 3 изображена структура ИСУ, где x ( t ) - вектор состояния объекта управления (ОУ), X d -«задающий сигнал» (цель управления), e(t ) - ошибка управления, вычисляемая как разность состояния ОУ и задающего сигнала: e(t ) = x ^ — x(t ) . На вход НР подаётся вектор ошибки управления: ошибка управления e(t ) , интегральная ошибка управления ie = J edt и производная ошибки управления e ( t ) .

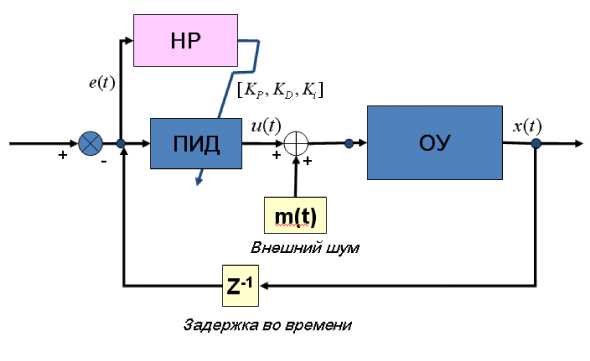
Рис. 3. Структура ИСУ

Структура НР представлена на рис. 4.

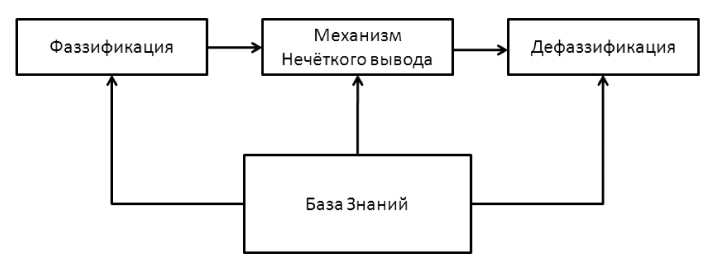
Рис. 4. Структура НР

НР состоит из следующих блоков:

• -    База Знаний, включающая базу нечетких правил и базу данных.

• -    База нечетких правил состоит из множества правил типа «если – то». База данных содержит информацию о типах и параметрах функций принадлежности, используемых в нечетких правилах.

• -    Механизм нечеткого вывода.

• -    Блоки фазификации и дефазификации. Блок фазификации преобразует входное, точное, значение в нечеткое значение. Блок дефазификации, наоборот, преобразует значения нечеткого множества в выходное, четкое значение.

Выходом НР является вектор значений коэффициентов усиления, которые поступают в ПИД-регулятор для формирования управляющего воздействия:

t u (t) = Kp (t) e (t) + K (t) J edt + KD (t) e (t)                                  (1)

o

Таким образом, функционирование ОУ существенным образом зависит от выбранных коэффициентов ПИД-регулятора. Поэтому, для разработчиков системы управления становится весьма актуальной проблема эффективного способа выбора этих параметров для обеспечения высокого качества управления [5].

Рассмотрим технологию получения БЗ с помощью инструментария ОБЗ для двух типов управления.

Математическая модель системы

В качестве примера применения ОБЗ рассмотрим задачу управления неустойчивой динамической системой «движущаяся каретка - перевернутый маятник» (рис. 5).

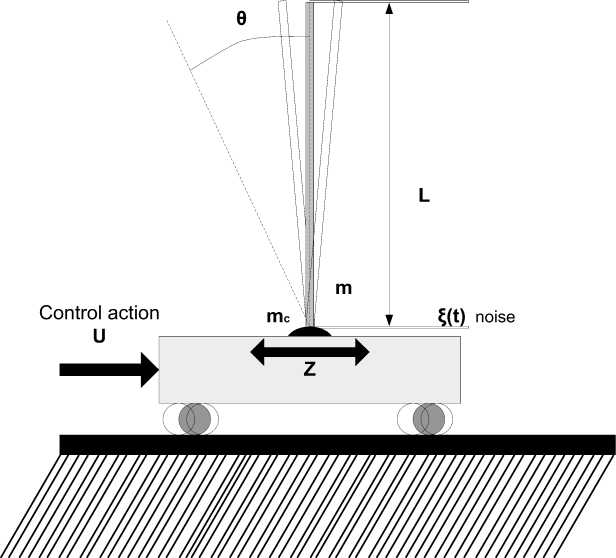
Рис. 5. Динамическая система «движущаяся каретка – перевернутый маятник»

Динамическое поведение этой системы при воздействии силы управления и описывается систе- мой дифференциальных уравнений второго порядка:

ycivO + xocO

и + ^(т) + а£ + a2Z - цХ0 civ0

<

0 =

Цх+Ц

^ 4   ЦХ°с²6 ^

,3 М х +ц^

— к0

и + ^(т) - aZ — a₂Z + mX(0²civ0 — 0%oc0) М х + М

В системе уравнений (1) Z и 6 - обобщенные координаты; у- ускорение свободного падения 9.8 m/sec2,^z - масса тележки, ц - перевернутого маятника (называемого «шест»),X - половина длины маятника, к и ai коэффициенты трения в Zи 9 соответственно, а2 - сила упругости тележки, £ -внешний стохастический шум.

Без управления маятник не может быть удержан в вертикальном положении [6]. Цель управления – сбалансировать положение маятника в условиях существенных ограничений на скорость и положение тележки, а также в условиях ограниченной силы управления. В этом случае для стабилизации необходимо выполнения условия θ = 0. Рассмотрим модель динамической системы c параметрами, представленную в табл. 2.

Таблица 2. Параметры системы

Параметры системы ц[кг] Ц [кг] Я [м] Коэфф. трения в0, к Коэфф. трения вZ a2 Сила упругости, a1 1.0 0.1 0.5 0.4 0.1 5.0 и следующими начальными условиями: ^0О0О J = [100.1](grad);^ZoZo] = [00] • Построим Matlab - модели для выбранных систем управления.

Проектирование нечеткого ПИД -регулятора в ОБЗ

Для создания нечеткого регулятора в ОБЗ получен обучающий сигнал (ОС) на ситуации с внешними воздействиями (шум с распределением Гаусса). На рис. 6-8 показаны спроектированные с помощью ОБЗ функции принадлежности.

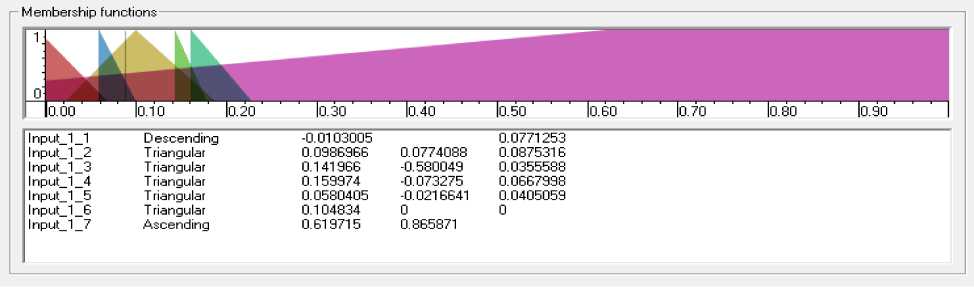
Рис. 6. Функции принадлежности для первой входной переменной

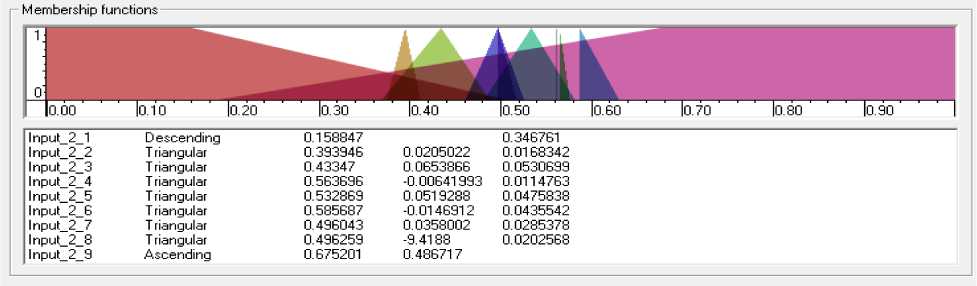
Рис. 7. Функции принадлежности для второй входной переменной

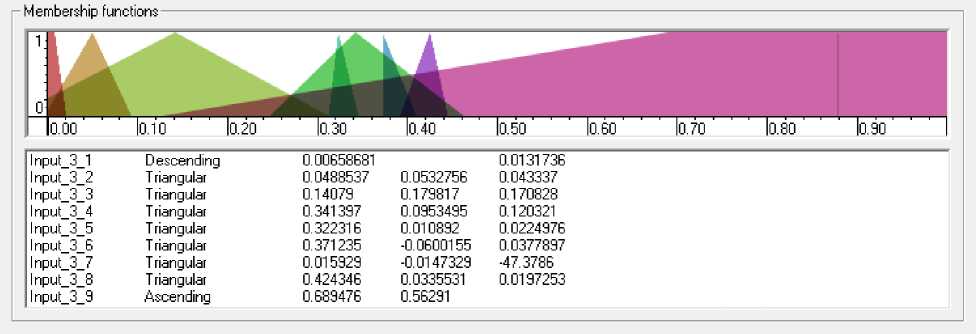
Рис. 8. Функции принадлежности для третьей входной переменной

Построим базу знаний в интеллектуальном инструментарии ОБЗ для скользящего типа управления.

Проектирование регулятора с СР в ОБЗ

Для создания НР в ОБЗ получен ОС на ситуации с внешними воздействиями (шум с распределением Гаусса). На рис. 9-11 показаны спроектированные с помощью ОБЗ функции принадлежности [7, 8].

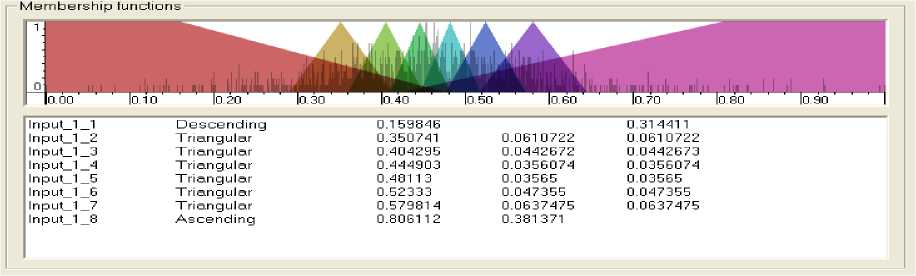
Рис. 9. Функции принадлежности для входной переменной S

— Membership functions

1 0
	обо' ' ' |0.10' ' ' |0.20 ' ' |0.30 ' ' ' |о.4о’ '       |о.5О ' ' KlGQ '        ^70            |о.во ' ■ ■ Го.ЭО " ■ ■

lnput_2_1	Triangular	0.268341	0.534742	0.534742
lnput_2_2	Triangular	0.547825	0.0222034	0.0222034
lnput_2_3	Triangular	0.566162	0.01 43389	0.01 43389
lnput_2_4	Triangular	0.579155	0.011552	0.011552
lnput_2_5	Triangular	0.591398	0.01 28456	0.01 28457
lnput_2_6	Triangular	0.604815	0.01 38922	0.01 38922
lnput_2_7	Triangular	0.62434	0.0250169	0.0250171
lnput_2_8	T riangular	0.818447	0.361 793	0.361 793

Рис. 10. Функции принадлежности для входной переменной dS

Output_1 _1	Descending	0.00342236		0.00419171
Output_1 _2	Triangular	0.0592487	0.0649892	0.231639
Output_1 _3	Triangular	0.294834	0.0603022	0.0131966
Output—1 _4	Triangular	0.493055	0.232442	0.139407
Output_1 _5	Triangular	0.740809	0.167613	0.309692
Output_1 _6	Ascending	0.997795	0.00876843

Рис. 11. Функции принадлежности для выходной переменной U

Membership functions

Сравнение результатов моделирования

Будем рассматривать модель динамической системы c параметрами, представленными в табл. 3.

Таблица 3. Параметры системы

Параметры системы ц [кг] Ц [кг] X [м] Коэфф. трения в 0, к Коэфф. трения в Z а2 Сила упругости, a1 1.0 0.1 0.5 0.4 0.1 5.0 и следующими начальными условиями:^0oOoJ = [100.1](grad);^ZoZo] = [00]• Весовой параметр w = 5.9.

Непредвиденная ситуация 1

Шум Гаусса (максимальная амплитуда = 2); Задающий сигнал = 0.

Сравнение работы регуляторов (скользящий режим и ПИД-коэффициенты) в непредвиденной ситуации 1 (рис. 12-15)

Pendulum angle

~ X -         ^^WAWfp'

SCO(PID) SCO(Sliding mode)

Рис. 12. Изменение угла маятника

Time

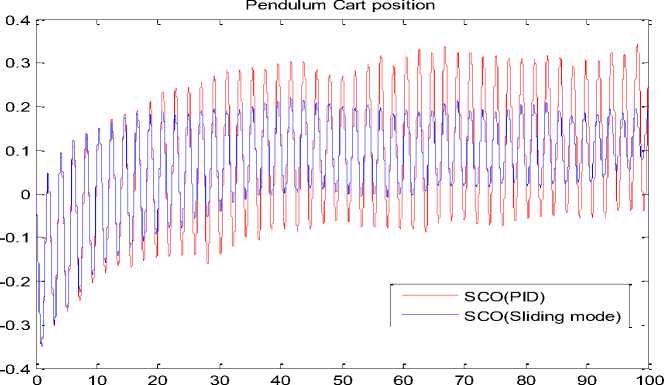
Рис. 13. Изменение положения каретки

Control force

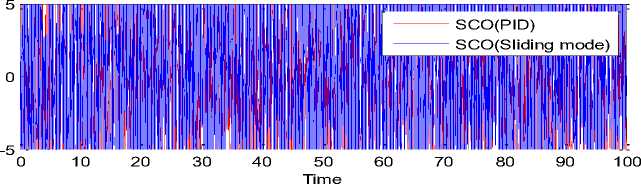
Integral control force

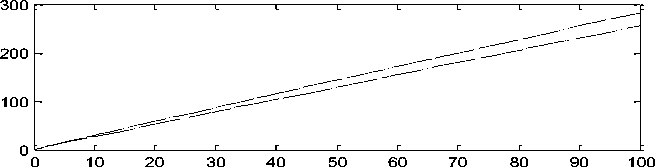
Time

Рис. 14. Изменение силы управления

Control error

0.2

-0.2 t____________E____________Г____________Е____________Е____________Г____________Г____________Е____________Е____________Е____________t

. 0     10    20    30    40    50    60    70    80    90    100

Time

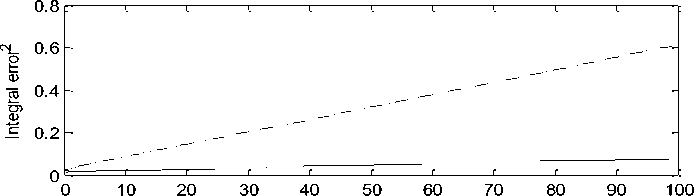
Integral quadratic error

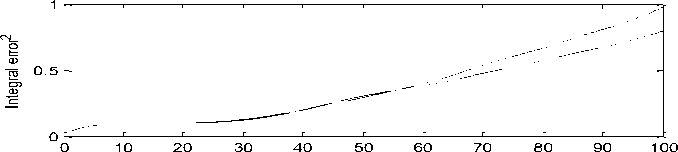
Time

. Изменение ошибки управления и интегральной квадратичной ошибки управления

Непредвиденная ситуация 2

Шум Гаусса (максимальная амплитуда = 2,5); задержка в каналах измерения = 0.001; задающий сигнал = 0.

Сравнение работы регуляторов (СР и ПИД-коэффициенты) в непредвиденной ситуации 2 (рис. 16-19).

Pendulum angle

0.2

SCO(PID)

SCO(Sliding mode)

0.15

0.1

"О

X

0.05

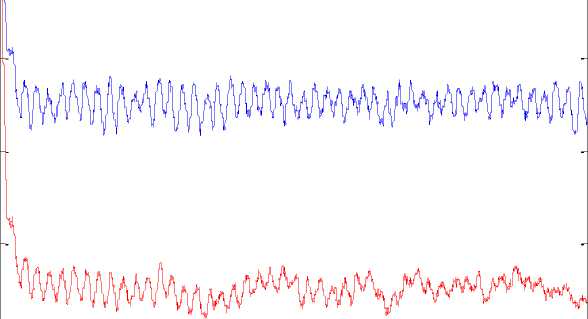
0     10    20    30    40    50    60    70    80    90    100

Time

Рис. 16. Изменение угла маятника

-0.05

Pendulum Cart position

Time

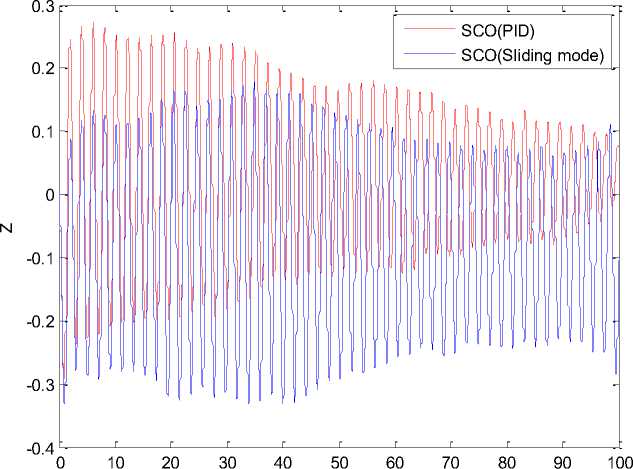
Рис. 17. Изменение положения каретки

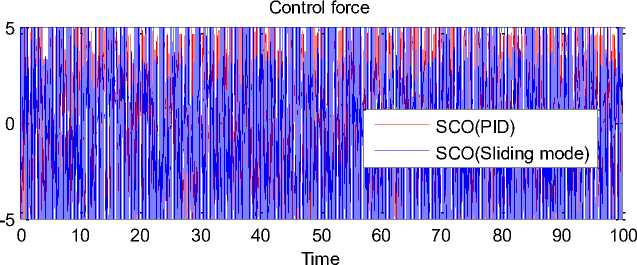
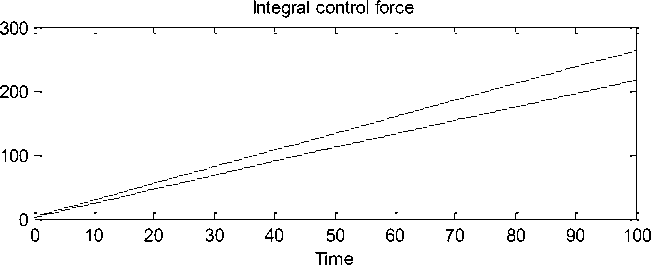
Рис. 18. Изменение силы управления

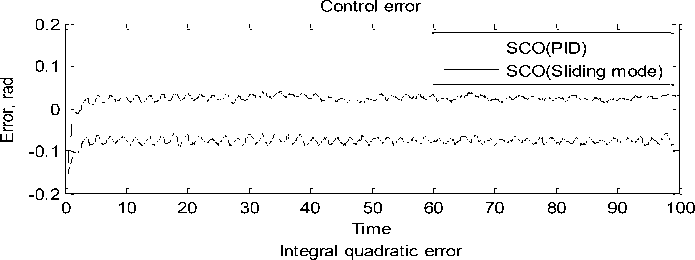
Time

Рис. 19. Изменение ошибки управления и интегральной квадратичной ошибки управления

Вывод

Из представленных результатов видно, что БЗ, спроектированные в ОБЗ, справляются с целью управления, причем в одном случае лучше использовать скользящий режим управления, а в другом, на ПИД-управлении.

Заключение

В этой статье показано сравнение двух типов управления – нечеткого скользящего типа управления и нечеткого ПИД-управления. Показана интеллектуальная структура обоих систем управления. Проведено сравнение, которое показало, что оба типа управления являются эффективными и способны достигать цели управления даже в непредвиденных ситуациях управления. Стоит отметить, что тип управления с СР в одном из случаев является менее эффективным, чем другой и достигает цели управления, но ресурса управления требует меньше, что может оказаться привлекательным для систем, которые не обладают мощным ресурсом управления.

Проектирование робастных ИСУ на основе такого подхода требует минимума исходной информации, как о поведении ОУ, так и о внешних возмущениях. Таким образом, новый разработанный инструментарий ОБЗ может строить робастные интеллектуальные системы управления, способные функционировать на множестве как обучающих (типовых), так и новых (непредвиденных) ситуаций управления для систем, использующих скользящий режим управления.