Телевизионное обнаружение объектов при малом количестве пространственно совпадающих реализаций сигнала в кадрах видеопоследовательности

Н елинейные методы фильтрации, основанные на максимизации (минимизации) отсчетов яркости видеопоследовательности представляют интерес как для визуализации динамических процессов [1], когда число пространственно совпадающих реализаций сигнала в кадрах видеопоследовательности достаточно мало, так и для других практических задач, в частности, для видеонаблюдения в реальном времени следов движения малоразмерных объектов, кратковременно появляющихся на неподвижном фоне.

Сущность данных нелинейных методов фильтрации заключается в сравнении цифровых кодов элементов кадра с цифровыми кодами соответствующих элементов кадра, полученного в результате предыдущего срав-

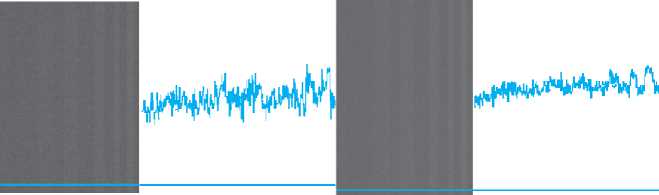
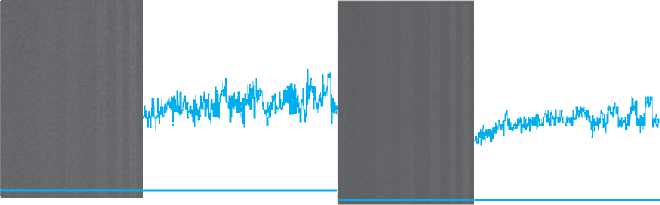
Рис. 1. Изображения тестовых полос на равномерном фоне и осцилограммы сигнала вдоль выделенной строки. Слева исходное изображение, справа – результаты обработки путем максимизации (вверху), путем минимизации (внизу)

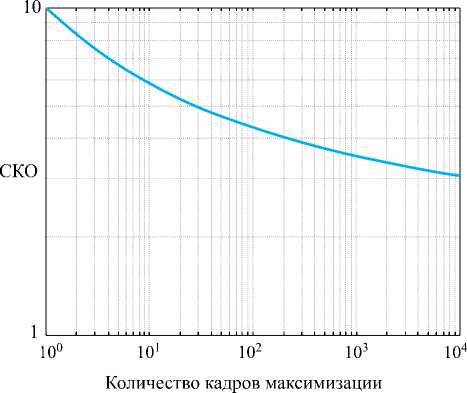
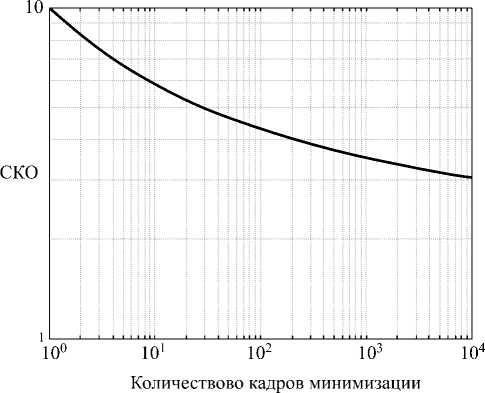
Рис. 2. Результаты моделирования изменения среднеквадратического отклонения (СКО) на выходе максимизирующего (слева) и минимизирующего (справа) фильтра

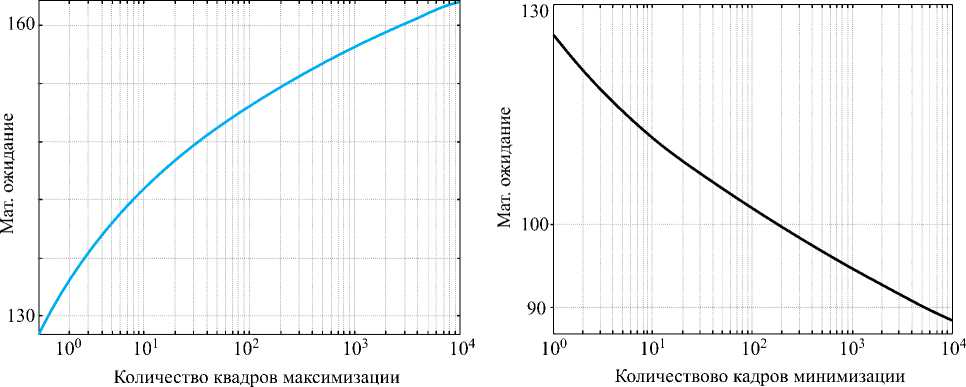
Рис. 3. Результаты моделирования сдвига математического ожидания на выходе максимизирующего (слева) и минимизирующего (справа) фильтра

нения, вычислении максимальных (максимизация) или минимальных (минимизация) значений цифровых кодов.

На рис. 1 представлены осцилограм-мы сигнала тестовых полос на равномерном фоне, характеризующие разброс значений яркости в изображении вдоль выделенной строки (дисперсию шума) в исходном одиночном кадре видеопоследовательности и в обработанном. Как видно из рис. 1, дисперсия шума в изображении, обработанном путем максимизации или минимизации существенно меньше, чем в исходном одиночном кадре видеопоследовательности, а ма- тематическое ожидание смещается относительно исходного значения.

На рис. 2, 3 представлены результаты моделирования в виде графиков для параметров выходного распределения, получаемых в результате нелинейной обработки методом максимизации (минимизации). Из данных графиков видно, что с ростом числа кадров обработки СКО выходного шума уменьшается и не зависит от входного СКО шума. При 20 кадрах обработки оно достигает значения 1,9, при 100 кадрах – значения 2,3, а при увеличении количества кадров обработки до 100 000 СКО уменьшается в 3,6 раза. Вместе с тем при обработке происходит сдвиг математического ожидания, который зависит как от числа кадров обработки, так и от входного СКО.

Максимизация эффективна при обработке сигнала объектов с положительным контрастом, а минимизация - при обработке сигнала объектов с отрицательным контрастом при априорно неизвестном числе реализаций сигнала в кадрах видеопоследовательности, в частности, когда число этих реализаций невелико по сравнению с общим числом кадров, содержащихся в этой видеопоследовательности.

Сравним изменение отношения сигнал-шум в зависимости от числа реализаций сигнала 1 ≤ k ≤ n в смеси с гаус-

совским шумом в видеопоследовательности из n кадров после ее обработки методом линейного усреднения отсчетов яркости, после их максимизации (минимизации).

С учетом независимых флуктуаций шума как на фоне, так и на сигнале исходное отношение сигнал-шум Ψ₁ составляет

% = Uc /(о, V2), где Uс – среднее значение (математическое ожидание) сигнала, σ1 – СКО входного шума.

После линейного усреднения отсчетов яркости видеопоследовательности, состоящей из n кадров, при наличии в ней k реализаций сигнала отношение сигнал-шум на выходе Ψ_2k составит

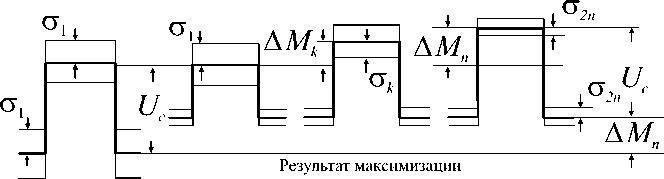
Исходный      одна реализация     А-реализаций      /7 реализаций сигнал         из п                 из п               из и

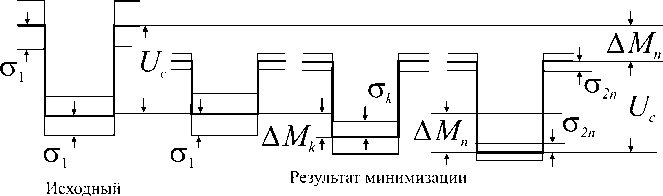
сигнал          одна реализация А-реализаций »реализаций из /7                      ,„                      ИЗ 77

Рис. 4 Исходный сигнал и результат максимизации (вверху) и минимизации (внизу) при изменении числа k реализаций сигнала в видеопоследовательности из n кадров с учетом шума на уровне сигнала

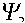
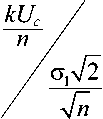
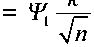
Таким образом, после линейного усреднения отношение сигнал-шум в зависимости от числа реализаций сигнала 1 ≤ k ≤ n изменяетс _– я в пределах Ψ₂₁ ≤ Ψ₂ ≤ Ψ_2n , где Ψ₂₁ = Ψ₁/√n – отношение сигнал-шум, получаемое при единственной реализации сигнала в видеопоследовательности из n кадров, а –

Ψ 2n = Ψ 1 /√n – отношение сигнал-шум, получаемое при реализациях сигнала в каждом из n кадров видеопоследовательности.

Рассмотрим отношение сигнал-шум после максимизации и минимизации ( рис. 4 ).

Из рис. 4 видно, что при максимизации и минимизации, кроме сдвигов математического ожидания уровня фона и математического ожидания уровня сигнала, изменяется величина СКО шума на сигнале σ_k . Это изменение лежит в пределах σ₁ ≤ σ_2k ≤ σ_2n , где σ_2n – СКО шума после обработки при k = n (т. е. при наличии реализаций сигнала во всех кадрах видеопоследовательности).

Таким образом, после обработки отношение сигнал-шум при k реализациях сигнала в видеопоследовательности, состоящей из n кадров, составит

Uc -(∆Mn-∆Mk)

22 σ _{2 n} + σ _{2 k}

Ψ1σ12-(∆Mn-∆Mk)

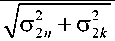
Соответственно при изменении k от

1 до n величина Ψ_2k меняется в пределах

Ψ 1 σ 1 2 -∆ M n σ ₂ ² _n + σ ₂ ² _k

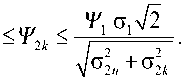
Таким образом, повышение отношения сигнал шум (т.е. Ψ_2k > 1 ) в результате максимизации (минимизации) достигается при условии:

^ 1 0,7 2 - ( A M n -A M k ) > ДГ^

Выполнение данного условия зависит от числа реализаций сигнала k, от исходного отношения сигнал-шум Ψ1, исходного СКО σ1 и от числа обрабаты- ваемых кадров n.

Рассмотрим предельные случаи, когда k = 1 и k = n . В первом случае

^i =  Ua 7°2 n +°?

^2 k O^UA\M )

а во втором –

^ =^ 2 n

V ₂ k    O i

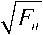
Тогда для того, чтобы при k = 1 выполнялось F ₁ ≤ 1 необходимо

Uc J ^2 n + ^2 <^iV2(Uc -A Mn), а с учетом того, что Ψ1 = Uc/σ1, получим условие:

A M n / ^O ,

° 2 n ±°_L

< У , .

При числе реализаций 1 < k < n данное условие определится соотношением:

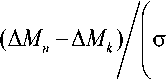
i 2 : г

]^

У

< ^ 1

На рис. 5 показаны графики зависимостей отношения сигнал-шум от числа реализаций k сигнала в n = 20 кадрах видеопоследовательности для линейного усреднения и для максимизации (минимизации). Для линейного усреднения при n = 20 величина сигнала, в зависимости от числа его реализаций в смеси с шумом, будет меняться от 0,05 до 1 относительно потенциально достигаемого значения. При этом величина СКО выходного шума составит ≈ 0,22 относительно входного СКО. График для максимизации (минимизации) построен приближенно путем аппроксимации единичного и потенциально

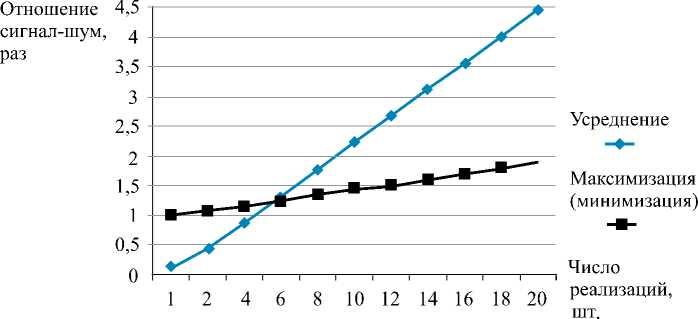
Рис. 5. Зависимость отношения сигнал-шум от числа n реализаций сигнала в n = 20 кадрах видеопоследовательности

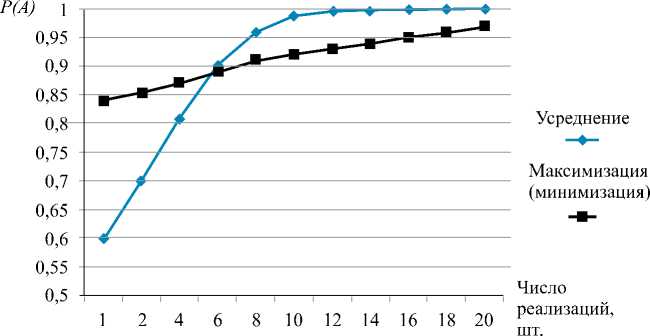
Рис. 6. Зависимость вероятности правильного обнаружения Р от числа n реализаций сигнала в n = 20 кадрах видеопоследовательности

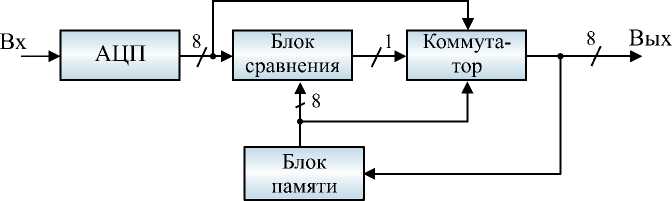
Рис. 7. Структурная схема максимизирующего (минимизирующего) фильтра

достигаемого отношения сигнал-шум, равного ≈1,9.

Вероятность правильного обнаружения объекта с положительным конт- растом при максимизации определяется как

P+= 1 - P(^вых > f^), где

Р ( ^ выых >  V_n p_p ) = I f (^ ) ^

∞ вых пop вероятность превышения случайной величины ξвых (выходным шумом) порогового отношения сигнал-шум Ψпор, кратного ее среднеквадратическому отклонению.

Вероятность правильного обнаружения объекта с отрицательным конт- растом при минимизации аналогичным образом определяется как

P =1-P(^

пop

P [5- s (-^op)] = J f №.. )^.

вых

-to

вероятность того, что случайная величина ξвых окажется меньше порогового отношения сигнал-шум (Ψпор), кратного ее среднеквадратическому отклонению. В силу симметричности гауссова распределения вероятности P+ и P–численно совпадают. На рис. 6 приведены графики зависимостей вероятности правильного обнаружения сигнала в зависимости от числа k его реализаций в n = 20 кадрах видеопоследовательности для линей- ного усреднения и для максимизации (минимизации).

Как видно из рис. 5, 6 , при числе реализаций n < 5 в видеопоследовательности из n = 20 кадров нелинейная фильтрация более эффективна, чем линейное усреднение. Таким образом, можно сделать общий вывод о том, что существенное преимущество нелинейной обработки видеопоследовательности достигается при числе реализаций сигнала в смеси с гауссовым шумом, не превышающим целого значения числа √n , где n – общее число кадров видеопоследовательности [2].

Для наблюдения в реальном времени следов объектов, появляющихся на неподвижном фоне, целесообразна аппаратная реализация нелинейной фильтрации, которая может быть вы- полнена на программируемых логических интегральных схемах (ПЛИС) в соответствии со структурной схемой, представленной на рис. 7.

Нелинейный фильтр содержит аналого-цифровой преобразователь (АЦП), блок памяти, блок сравнения и коммутатор. АЦП осуществляет преобразование телевизионного сигнала в цифровой код, который поступает на вход коммутатора и на вход блока сравнения, на второй вход которого поступает цифровой код с блока памяти. Блок памяти предназначен для запоминания цифрового телевизионного кадра. При этом он работает в режиме считывание – модификация – запись и после считывания резуль- тата предыдущего сравнения запоминает результат текущего сравнения – цифровой код с выхода коммутатора. Блок сравнения производит сравнение текущего и задержанного на время кадра цифровых кодов и формирует управляющий сигнал «≥» в случае максимизации (или «≤» в случае минимизации). Управляющий сигнал переключает коммутатор, на выходе которого формируется либо текущий цифровой код от АЦП, либо предыдущий цифровой код от блока памяти. Если фильтр максимизирующий, то блок памяти предварительно обнуляется, если фильтр минимизирующий, то в блок памяти предварительно заносятся максимальные значения отсчетов яркости.

При необходимости одновременной работы с сигналом разной полярности по отношению к фону возможна реализация двухканальной схемы ( рис. 8 ) нелинейного фильтра.

Двухканальный нелинейный фильтр содержит максимизирующий и параллельно работающий минимизирующий фильтр, выполненные в соответствии с приведенным выше описанием. Для формирования общего бинарного сигнала от объектов разной полярности первый и второй выходы фильтра подключаются к соответствующим блокам сравнения с порогом, выходы которых объединяются через схему ИЛИ ( рис. 9 ).

Выводы

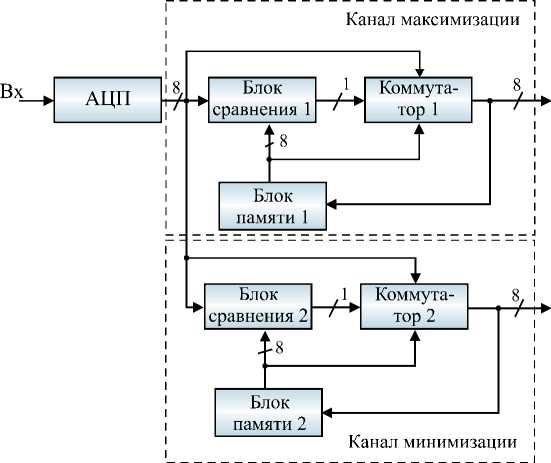
Рис. 8. Структурная схема двухканального нелинейного фильтра

Вых 1

Вых 2

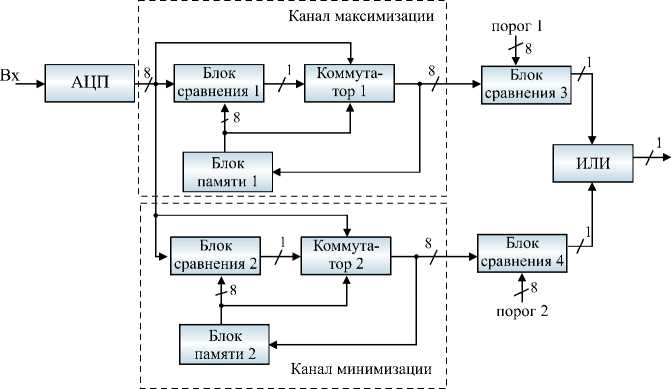
Рис. 9. Схема двухканального нелинейного фильтра с пороговыми устройствами

• 1    Преимущество нелинейной обработки видеопоследовательности на основе максимизации по сравнению с линейным усреднением достигается при числе реализаций сигнала в смеси с гауссовым шумом, не превышающим целого значения числа √n , где n – общее число кадров видеопоследовательности.

• 2    Потенциально достигаемое повышение отношения сигнал-шум при пространственном совпадении реализаций сигнала в каждом из кадров видеопоследовательности изменяется в пределах ≈1,9 ÷ 3,6 при числе кадров обработки от 20 до 100 000 ■

  Литература

  
  

  • 1.    Е.В. Андреева, Н.П. Корнышев, Н.С.Никитин, Н.И. Смирнов, А.В. Хаймин. Способ визуализации структуры газоразрядного свечения объекта в электромагнитном поле. Заявка №2009125/09/28(034719) МПК G03B41/00. Решение о выдаче патента от 28.12.10 г.

  • 2.    Н.П. Корнышев, А.В. Лифар, А.В. Хаймин. Сравнение отношения сигнал-шум и вероятности правильного обнаружения после максимизации и линейного усреднения видеопоследовательности. /Труды ХХ Международной научнотехнической конференции «Современное телевидение». – М.: ФГУП МКБ «Электрон», март 2012.