Тематическая классификация гиперспектральных изображений по показателю сопряжённости

Постановка задачи

В последние годы всё большую актуальность приобретает задача тематической классификации гиперспектральных изображений. Число публикаций по этой тематике быстро нарастает. В качестве примера приведём классическое учебное пособие [1] и одну из работ коллективов Московского государственного университета геодезии и картографии, Московского физико-технического института ЗАО «НПО «Лептон» [2].

Многоспектральные и гиперспектральные изображения, получаемые при дистанционном зондировании земной поверхности, позволяют решать широкий круг тематических задач геологии, климатологии, лесного хозяйства, океанологии, землепользования, контроля водных ресурсов и т. д. При этом для автоматизированной сегментации часто используются алгоритмы пороговой обработки, гиперпараллелепи-педного метода и кластерного анализа. Популярным программным комплексом, в котором реализованы функции кластерного анализа для обработки гиперспектральных изображений, является пакет ENVI [3].

Программный комплекс ENVI включает функции обработки и глубокого анализа гиперспектральных снимков, радиометрической и геометрической коррекции, улучшения качества изображений, дешифрирования и классификации и др. Для решения указанных задач в пакете могут использоваться различные алгоритмы. Одним из таких алгоритмов, который предлагается для решения задач тематической классификации, является алгоритм классификации с помощью метода спектрального угла [4], [5]. При этом задача ставится и решается следующим образом.

Введём в рассмотрение N ×1-вектор, характеризующий j -й гиперпиксель изображения:

xj = [ x1 ( j ) , x 2 ( j )’—’ xi ( j ) ’-’ xN ( j ) ] T , (1) где xi(j) - значение интенсивности отражения регистрируемого объекта в i-м спектральном диапазоне в j-й точке гиперспектрального изображения по пространственной координате. Задача контролируемой классификации состоит в конструировании решающей функции f : Rn ֏{0,1,2,…,k}, которая для каждого вектора xj вырабатывает решение о его принадлежности к некоторому классу.

Будем полагать, что для каждого типа (класса) задано M обучающих векторов, так, что для каждого k -го класса может быть составлена N × M -матрица:

X k = [ x 1 ( k ), x ₂( k ),..., x M ( k )], k = 1, K .           (2)

Реализованный в ENVI алгоритм классификации, основанный на методе спектрального угла, описывается следующим образом. Для каждого класса вычисляется вектор ͞ x ( k ):

1M x (k) = 77 Exj (k), k = 1, K ,                  (3)

M ~"t j который является прототипом k-го класса. Гиперпиксель, характеризующийся вектором признаков xj, относят к k-му классу, если достигается максимум пока- зателя спектрального угла:

= cos ¹

/ i------------------------------\ -1 "A

N       N

JE X2 (j)E X2 (k)

V i =1              i =1

NL

E X ⁽ j ) X ^{( k} )

i = 1

V

В настоящей работе исследуется алгоритм, который можно рассматривать как его обобщение. В данном случае вместо вычисления угла между классифицируе- мым вектором и средним вектором класса предлагается вычислять угол между вектором и подпространством, натянутым на множество векторов из этого класса.

Данный метод был впервые описан в работе [6]. Дальнейшее развитие получил в работах [7], [8]. В работах [9], [10], [11] описано применение метода для распознавания лиц. В настоящей работе приводятся результаты экспериментов на тестовых гиперспектральных изображениях, показывающие более высокое качество классификации по сравнению с методом спектрального угла.

Описание алгоритма классификации

Предлагаемый классификатор основан на использовании так называемого показателя сопряжённости с подпространством, натянутым на векторы признаков образов объектов из заданного класса. Пусть x j - вектор признаков, являющийся образом j -го гиперпикселя, предъявленного для установления близости к k -му классу, а X _k – N × M -матрица (2), составленная из обучающих векторов (гиперпикселей) этого класса.

Алгоритм строится на основе следующих соотношений. Для каждого ( k -го) класса формируется N × M матрица Q k :

Q k = X k [ X T X k ] - 1 X T , k = 1, K . (5)

Решающая функция f ( x ) строится следующим образом. Вектор x j является образом искомого объекта (гиперпикселя) и принадлежит m -му классу, т.е. f ( x ) = m , m = 1,2,... k , если

R m ( j ) = ma ^x R k ( j ) , ⁽⁶⁾ где

R k ( j ) = "Qx . (7) x ^T j x j

Таким образом, для построения процедуры распознавания необходимо на этапе обучения для каждого предполагаемого типа (класса) с использованием матрицы (2) построить по соотношению (5) N × M -матрицу Q k . Подчеркнём, что для каждого вектора x j признаков, являющегося образом некоторого гиперпикселя, максимум показателя сопряжённости R k ( j ) ищется по всем классам гиперспектрального изображения.

Нетрудно заметить, что при использовании описанного алгоритма качество классификации будет существенным образом зависеть от способа задания матриц классов (2). Простейший способ формирования матриц X _k – случайный выбор заданного числа векторов на участке изображения, принадлежащего известному классу. Для полной характеристики класса в этом случае число отбираемых векторов должно быть достаточно большим. Однако это увеличивает вычислительную сложность алгоритма и может приводить к ошибкам классификации вследствие ухудшения обусловленности матрицы X ^T _k X _k .

Снижение вычислительной сложности и повышение качества классификации может быть достигнуто путём разбиения класса на подклассы. Процедура строится следующим образом. На первом шаге из всего множества M векторов выбираются два (обозначим их x 1 , x M ) наиболее «удалённых» вектора, для которых величина

^R 1, M = x^Xl x M ^/U x lll ll x M II ⁽⁸⁾ минимальна. Затем из оставшегося множества векторов к ним присоединяется по одному вектору ( x 2 , x M- 1 ), для которых величины

R 1,2 = ^X TI 2 2)/|| ^X 1|| || x 2 ||, ⁽⁹⁾

R M -1, M = ( MM -1 ^Xm V|| ^XM -1|| ll x M II ⁽¹⁰⁾

принимают максимальные значения. Пары векторов x1, x2 и xM-1, xM образуют два подпространства, описываемых матрицами X1,2 и XM-1,M соответственно. Далее определяются следующие два вектора x3, xM-2, бли- жайшие к этим двум подпространствам по критерию максимальной сопряжённости:

^R 1,2,3 =

V TX T X 1 ¹ X T V

^Х 3^Л1,2 L ^Л1,2^Л1,2 ] ^Л1,2 ^Х 3

T x ^T ₃ x ₃

^RM - 2, M - 1, M

VT X    Гх T   X    T1 XT xm-2^m-1,M L m-1,m m-1,m ]    M-1,M

. (12)

x M - 2

кукуруза и соя, находятся на раннем этапе и покрывают меньше 5% изображения. Разработчиками тестового изображения предложен сокращённый вариант, включающий 200 спектральных полос изображения с разбиением изображения на 16 классов, притом не все из них являются взаимоисключающими. В частности, на снимке имеется неразмеченная область, которая не отнесена ни к одному из 16 классов. Данная область при проведении эксперимента не использовалась. Тестовое изображение, разбитое на классы, приведено на рис. 1, неразмеченная область показана белым цветом.

а)

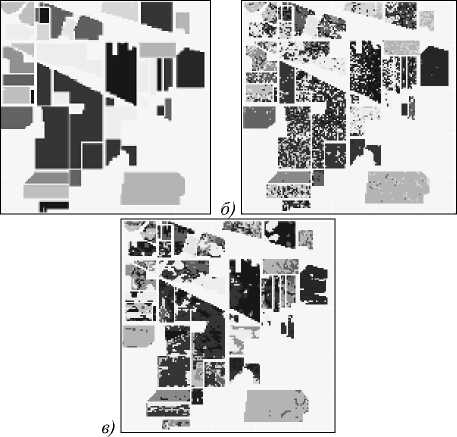
Рис. 1. Тестовое изображение с разбиением на классы:

• а)    исходное изображение;

• б)    классификация по критерию спектрального угла;

• в)    классификация по показателю сопряжённости

В эксперименте исследовалось достижимое качество классификации по показателю сопряжённости в сравнении с методом спектрального угла. В качестве критерия качества использовалось отношение числа правильно распознанных гиперпикселей к общему числу гиперпикселей тестового изображения. Поскольку доступным для экспериментов было только одно тестовое изображение без априорного разбиения на тестовую и обучающую части, для оценки качества алгоритмов распознавания применялась процедура скользящего контроля. Эта процедура позволяет разбить исходные данные N различными способами на две непересекающиеся подвыборки, одна из которых будет обучающей, а другая – тестовой. При этом тестовая выборка имеет долю 1/ N векторов, а обучающая – ( N –1)/ N .

Отметим, что полученное случайное разбиение обладает существенным недостатком – несбалансированностью количества представителей разных классов. В случае отсутствия (или недостаточного количества) представителей одного или нескольких классов в обучающей выборке качество классификации может быть существенно снижено. Для преодоления проблемы несбалансированности использовалась процедура стратифицированного скользящего контроля, разбивающего данные таким образом, что общая доля векторов каждого класса сохраняется как в тестовой, так и в обучающей выборке. При этом возможна оценка обобщающей способности алгоритма.

В табл. 1 и на рис. 1 а и б представлены сравнительные (по показателю сопряжённости и методу спектрального угла) результаты выполнения процедуры стратифицированного скользящего контроля с 5 блоками. На рисунках белыми точками на всех классах отмечены неверно классифицированные гиперпиксели.

Таблица 1. Результаты классификации

№ этапа	% верных классификаций
	по показателю сопряжённости	по методу спектрального угла
1	62,7	50,9
2	64,1	48,7
3	61,0	48,7
4	61,6	49,4
5	65,2	50,1
Средний результат	62,9	49,6

В экспериментах исследовалась также описанная выше процедура разбиения класса на подклассы с использованием соотношений (8)–(12). В табл. 2 и на рис. 2 а приведены результаты классификации по показателю сопряжённости с предварительным разбиением каждого класса на 2 подкласса. На рис. 2 а , как и ранее, белыми точками на всех классах отмечены неверно классифицированные гиперпиксели.

Таблица 2. Результаты классификации с предварительным

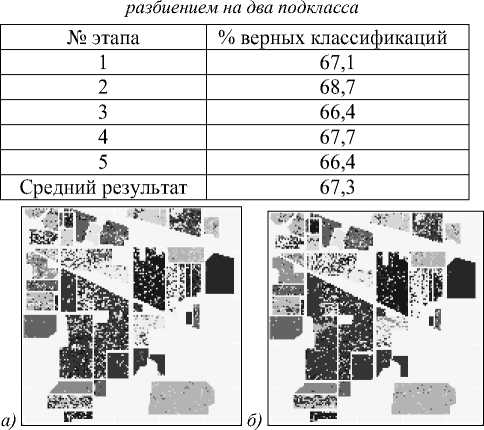
Рис. 2. Результат классификации: а) с разбиением на два подкласса;

б) с вычитанием среднего и разбиением на подклассы

Был проведён также эксперимент по проверке степени влияния на качество классификации преобразования, заключающегося в вычитании из всех векторов среднего вектора, вычисленного по всем гиперпикселям тестового изображения. В табл. 3 и на рис. 2 б приведены результаты работы классификатора, основанного на показателе сопряжённости, с предварительным вычитанием среднего вектора и разбиением классов на подклассы.

Таблица 3. Результаты с вычитанием среднего и разбиением на подклассы

№ этапа	% верных классификаций
1	71,2
2	71,8
3	71,2
4	74,0
5	69,6
Средний результат	71,6

Заключение

Приведённые эксперименты показывают возможность достижения более высокого качества тематической классификации с использованием показателя сопряжённости по сравнению с методом спектрального угла. Подчеркнём, что векторы признаков в данном случае должны иметь одинаковые размерности, а их компоненты – характеризовать одноимённые спектральные диапазоны. Если в качестве обучающих гиперпикселей для классифицируемых областей используются данные из разных библиотек, содержащих данные в разных спектральных шкалах, необходимо решать задачу предварительного приведения данных к унифицированной спектральной шкале путём их интерполяции.

Работа выполнена при поддержке Министерства образования и РФФИ (проекты №13-07-12030 офи_м, № 12-07-00581-а).