Температурная зависимость коэффициентов модели анизотропной пристеночной турбулентности для воды и воздуха

В модели анизотропной пристеночной турбулентности турбулентное течение жидкости рассматривается как течение анизотропной жидкости, анизотропия которой определяется когерентной системой вихрей, вытянутых по потоку [1], [2]. Кинематическими параметрами, которыми задается движение в точке потока в декартовых координатах x р x2, x3, являются скорость u и единичный вектор, задающий локальную анизотропию, - директор п ..

Все локальные величины, характеризующие состояние и движение системы, по определению считаются объемно осредненными. Для несжимаемой жидкости уравнения движения имеют вид [1], [2]:

= 0 (1) дxi du,   дp,„

Р — =   + Р f, dt    дx а d (тПп,) др у

Р— I I — I = —~ + g, + РF, dt ( dt J дxy    ‘‘ dU

Р,    Pjej + РijNj - giNi + Q - Ti", dt J J J Jдx-

где t - время, p - плотность жидкости, u i - скорость, p . - напряжения, f _ - плотность массовой силы, U- внутренняя энергия единицы массы, Q - интенсивность источника тепла, q . - поток тепла. Величины e ij , g, F _t называются соответственно обобщенным напряжением, обобщенной внутренней и обобщенной внешней массовой силой. Величина I характеризует осредненную инерционность структуры при повороте элементов вихревой структуры. По повторяющимся индексам предполагается суммирование от 1 до 3.

Определяющие уравнения учитывают специфику среды. В рассматриваемой модели они имеют вид

Pj = - Р ^у + Су + Ту,(5)

С У = Knа/ny,а- nа,у + nynpПа,р ),(6)

Ту = Р1 nan в e аР ninj + Ро ey,(

Ру = КуП, + K(n у - nji - nnаnia),(8)

g , = Xn, - (КРn, ),Р + KnanР,аnР,, ,(9)

q.=-(X о T.+X1 nj),

• д n,            1 1 д u, д u, | d д д . dn,

n i , = —^L, е_у = —I— i -+---I,— = —+ u , —, n, = —i -,

• ¹¹ дx_y ¹ 2 ^д x_y д x i J dt д t ¹ x_y dt

N i = n i ^- ® i a ⁿ а ,      N y = ⁿi,y ^- ® i a ⁿ а ,у , ² ® у = u у ^- u ji .

Здесь р - давление, T - температура, a j - напряжения, обусловленные наличием в среде вихревой структуры, т j - вязкие напряжения, X₀, X j , р₀, р_р K - коэффициенты модели, S j - символ Кронекера, х и к. - произвольные скалярная и векторная функции соответственно. Поскольку свойства жидкости вблизи твердой стенки определяются пристеночной вихревой структурой потока, то коэффициенты X₀, X 1 , р₀, P j , K могут зависеть от параметров, глобально характеризующих течение, например от числа Рейнольдса.

Характерными величинами, определяющими турбулентную вязкость и турбулентную теплопроводность жидкости, являются коэффициенты X₀, X 1 , р₀, P j . При течениях в трубе радиусом R и в плоском канале шириной 2 H их величины для воздуха при температуре T = 20 °С и при нормальном давлении найдены [1], [2] сравнением решений ряда задач с опытными данными: р₀ = 1,85^10^-6 Па^с, р 1 = 0,047 u * Па^с, X₀ = 0,28 Ru * Вт/ (мК (0,28 Hu * для^плоского канала), X 1 = 46,5 и * Вт/(м^К), где u , = 7т w / р - динамическая скорость. Определению зависимости коэффициентов р₀,

μ1, λ0, λ1 для воды и воздуха от температуры посвящена настоящая работа.

коэффициенты μ ₀ и μ ₁

Решение задачи об установившемся турбулентном течении несжимаемой жидкости (воды или воздуха) в круглой трубе при постоянной температуре в рамках рассматриваемой модели в цилиндрической системе координат r , φ, x (ось x – по оси трубы в направлении течения) имеет вид [1], [2]

u = ^u .[ ф ( ^ ) -Ф (1)], Ф© = F ( t ©), t © = [1 - 3 bR (1 -У ]^|/3 , (11)

На рис. 1 и 2 профили скоростей (точки) для течений воды и воздуха в гладкой трубе диаметром d = 80 мм и гладком канале шириной 2H = 80 мм при 0 °С или 10 °С и 100 °С, вычисленные с учетом формул (13) и (14), при разных числах Рейнольдса (Re = 2wR/ν для круга и Re = 4wH/ν для канала, w – средняя скорость) сравниваются с универсальным профилем скоростей [4]

usu

— = 5,75lgn + 5,5, n = —, u *

F ( t ) =

3 bR - 1 2 / ² -1

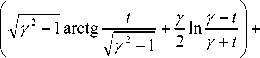
1 + 2e , y ² — t ln

4(2 Y ² - 1)    t ² + Y 2 — 1

+ —In I t⁴ 4

^^^^^B

t ²

e

t ²

⁺ 2 ^,

A = '' , 3ц_х b² R

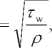
, = 20L 2_Ц;

2 y ² = 1 + 4 1 + 4 e , 5 = - , R

где b – постоянная интегрирования уравнения, задающего изменение директора по сечению потока, определяется экспериментально.

Определяя профили скоростей (11) при разных температурах с учетом теплофизических свойств обеих сред [7], [8] и сравнивая эти профили с универсальным профилем трубы [4]

- = 5,75lg ⁽ R - r ) u * + 5,5 , (12) u . v

где s - расстояние от твердой стенки до точки в потоке.

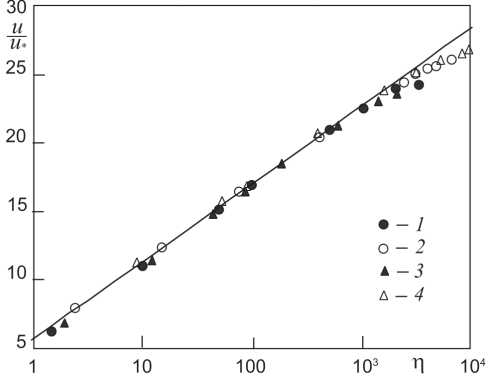
Рис. 1. Профили скоростей при течении воды в трубе и плоском канале при T = 10 °С, 100 °С. Кривая -универсальный профиль (16). Точки - результат расчета: 1 - труба, 10°, Re = 285000; 2 - труба, 100°, Re = 420000; 3 - канал, 10°, Re = 404000; 4 - канал, 100°, Re = 970000

где ν – кинематическая вязкость воды или воздуха, для каждого значения температуры получаем величины μ₀, μ₁ и b.

Ограничимся диапазоном температур от 0 до 100 °С. Как оказалось, коэффициенты μ0, μ1 для воды и воздуха при изменении температуры ведут себя различно. Для воды при 5 °С ≤ T ≤ 100 °С имеем b 4,80м-1, 0 (2,63 1,20lgT) 4 , 1 40u , (13) тогда как для сухого воздуха при 0 °С ≤ T ≤ 100 °С b = 4,80 м ■ 1, м0 = 2,0 • I0-6, M1 = u * (0,051 - 0,00012T ),(14)

где T – температура в градусах Цельсия, μ₀ и μ₁ – в Па ∙ с, u_* – в м/с .

Совершенно аналогично, сравнивая профили скоростей при течении несжимаемой жидкости в плоском канале шириной 2 H , полученные на базе рассматриваемой модели [1], [3], с универсальным профилем для канала

- = 5,75lg(H -^)U* + 5,5, (15) u * v получаем те же формулы (13) и (14). В формуле (15) (H – |y|) – расстояние от стенки канала до точки потока с координатой y, отсчитываемой от срединной плоскости канала перпендикулярно течению.

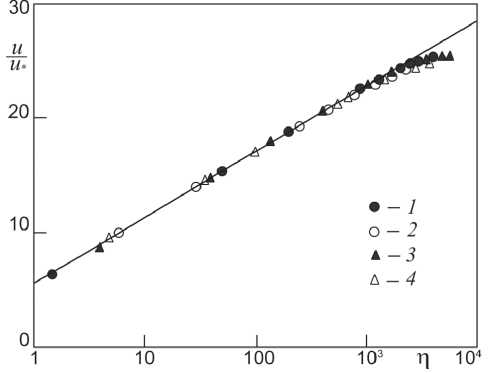
Рис. 2. Профили скоростей при течении воздуха в трубе и плоском канале при T = 0 °С, 100 °С. Кривая -универсальный профиль (16). Точки - результат расчета: 1 - труба, 0°, Re =243000; 2 - труба, 100°, Re = 227000; 3 - канал, 0°, Re = 510000; 4 - канал, 100°, Re =474000

Стоит отметить, что значения μ0, μ1 для воздуха при 20 °С, которые следуют из формул (14), близки указанным во введении значениям, которые ранее были получены на основе конкретных опытных данных.

коэффициенты λ ₀ и λ ₁

Процессы теплообмена в трубах и каналах описываются уравнением распространения тепла, которое в рамках данной модели следует из уравнений (4) и (10). Пусть в гладкой круглой по-лубесконечной трубе x ≥ 0 радиуса R требуется найти установившееся распределение температуры T ( r , x ) при установившемся турбулентном течении несжимаемой жидкости, при постоянной температуре стенки T _w и постоянной температуре T ₀ на входном сечении x = 0. В безразмерных переменных

pv c„

Pr =      , - =

X

(1,821g Re - 1,64)² .

Как и для коэффициентов μ0, μ1, зависимость коэффициентов λ0, λ1 от температуры для воды и воздуха различна. Для воды при течении в трубе при 5 °С ≤ T ≤ 100 °С она имеет вид

X 0 = G ( T )V T 78, X , = 12000 u ., G ( T ) = 0,0360 - 0,000211 T .(25)

T - T w T 0 - T w ,

5 = ^L,   X = x ,

RR

в цилиндрических координатах r , φ, x при Q = 0 уравнение распространения тепла имеет вид [1]

^4+^, (o — = ^₂ (y— d^    1^ ’ ^    ²^ I X x

W =

1 -        2 X 1 bR

I t ( ^ ) [ X _O +x 1 (1 - 1 ²(У) ] ]

Для воздуха

X 0 = u . R (0,30 - 0,001 T ), X 1 = 46,5 u . .        (26)

В формулах (25) и (26) T – температура в градусах Цельсия, λ₀, λ₁ – в Вт/(м ∙ К), R – в метрах, u _* – в м/с.

Следуя работе [3], при условии, что пристеночная турбулентность заполняет всю область течения, сравнением с эмпирическими формулами (21)–(23) можно получить аналоги формул (25) и (26) при теплообмене в плоском канале шириной 2 H . Для воды

X 0 = 0,5 G ( T )7 / 78, X ₁ = 12000 u ., G ( T ) = 0,0360 - 0,000211 T .(27)

²(^У     x 0 +X 1 (1 - 1 ²O

Для воздуха

X 0 = u . H (0,30 - 0,001 T ), X 1 = 46,5 u . .          (28)

где c_p – теплоемкость при постоянном давлении, ^p λ₀, и λ₁ – коэффициенты, через которые определяется поток тепла q_i по формуле (10), t (ξ) и Φ(ξ) – функции, определенные в (11).

Решение уравнения (18) с граничными условиями

При течении в канале числа Рейнольдса Re и Нуссельта Nu определяются формулами [5]:

4 wH

Re =----- ,

v

Nu =

2 X ₀ Гд®Л

X© J

где Θ – средняя массовая температура по сечению трубы, λ – коэффициент молекулярной те-

плопроводности, w – средняя скорость.

Значения числа Нуссельта Nu, вычисленные

при температурах воды и воздуха в диапазоне от нуля до 100 °С и при разных числах Рейнольдса Re, сравнивались со значениями Nu, которые при

тех же условиях течения для предельного числа Нуссельта Nu∞ даются соответственно работам [5], [9], [6] эмпирическими формулами:

Nu „

f Re Pr/ 8

2,

1 + ⁹⁰⁰ + 12,7, V- 1 Pr^/3 - 1 1

Re V 8 ( J

Nu „

RePr f 2

4,241n(Re V - /16) + 25,0 Pr^2/3 + 4,24 In Pr - 20,2

,(22)

Nu„ = 7,6 —3,6- + 0,0096Re °■ ⁸⁷Pr °■ ⁶ ° ⁵ ,       (23)

“ IgRe                      ,       v )

, © = - f© ( ^ , X ) u®d ^, (30) w ₀

где Θ – безразмерн а я температура, определяемая формулой (17), Θ – средняя массовая температура, ξ = y/H – безразмерная поперечная координата в канале, отсчитываемая от срединной плоскости канала.

На рис. 3 представлены графики зависимостей предельного числа Нуссельта Nu_∞ от числа Рейнольдса Re при течении воды в трубе и плоском канале при постоянной температуре стенок, вычисленные на основе решений [1], [2], [3] при температуре воды 10 °С и при 100 °С с использованием формул (13), (25) и (27) (точки), а также соответствующие графики формул (21)–(23) (кривые 1 – 3 для 10 °С; кривые 1 ´– 3 ´ для 100 °С). Поскольку для воздуха аналогичные зависимости вплоть до 100 °С различаются несильно, на рис. 4 приведены графики расчетных величин (точки) и формул (21)–(23) только при температуре 100 °С. Все расчеты проведены для трубы диаметром d = 80 мм и канала шириной 2 H = 80 мм. Как видим, результаты расчетов вполне удовлетворительно согласуются с эмпирическими формулами. Отметим, что при 20 °С для воздуха из формул (28) следуют значения λ₀, λ₁, указанные во введении.

Nu =

^^^^^s

4 X 0

d©

X© (d^

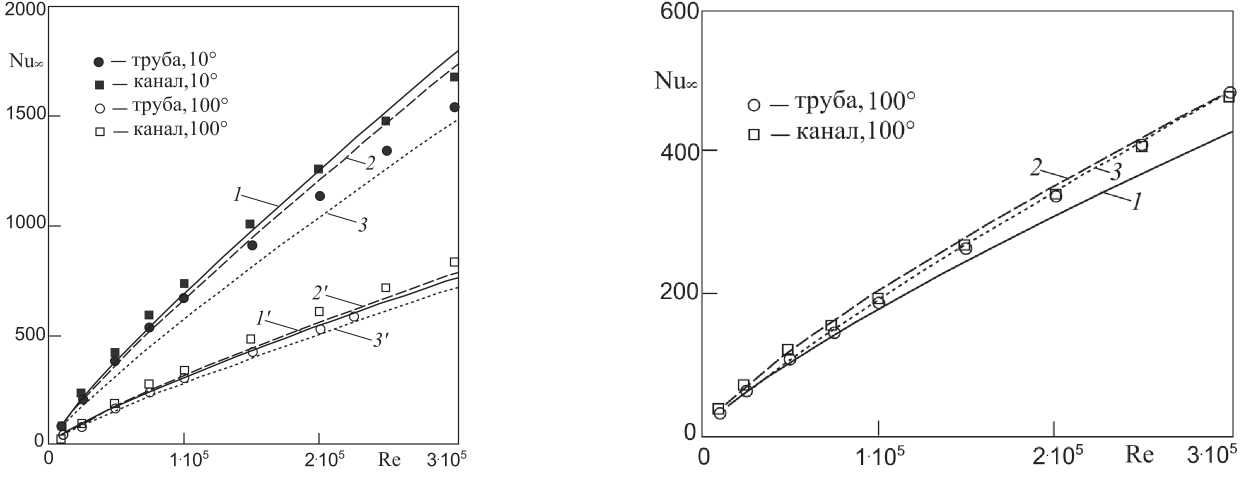
Рис. 3. Зависимость предельного числа Нуссельта Nu_∞ от числа Рейнольдса Re для воды в трубе и канале при T = 10 °С, 100 °С. Точки - результат расчета; кривые - графики эмпирических формул: 1 , 1' - (21) [5]; 2 , 2' - (22) [9]; 3 , 3' - (23) [6]

Рис. 4. Зависимость предельного числа Нуссельта Nu∞ от числа Рейнольдса Re для воздуха в трубе и канале при

T = 100 °С. Точки - результат расчета; кривые - графики эмпирических формул: 1 - (21) [5]; 2 - (22) [9]; 3 - (23) [6]

ЗАКЛЮЧЕНИЕ

Полученные в данной работе зависимости коэффициентов μ0, μ1, λ0, λ1 от температуры, с одной стороны, увеличивают круг задач, которые можно численно решать в рамках модели пристеночной анизотропной турбулентности, а с другой стороны, расширяют наши представления о тур-

булентности в таких широко используемых средах, как вода и воздух. В частности, очевидно наблюдаемое различие в поведении коэффициентов, определяющих турбулентную вязкость и турбулентную теплопроводность воды и воздуха при увеличении температуры сред.

* Работа выполнена при поддержке Программы стратегического развития (ПСР) ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.