Температурная зависимость теплоемкости и изменение термодинамических функций свинцового сплава ССУЗ с кальцием

В гидроэлектрометаллургии, гальванотехнике, аккумуляторном производстве и кабельной технике свинец и его сплавы широко используются в качестве материала анода и защитной оболочки. Несмотря на ряд разработанных новых анодных материалов и защитных покрытий, свинец, несомненно, останется основным материалом для крупномасштабных электрохимических производств и кабельной техники. В этой связи особо актуален вопрос правильного выбора легирующих элементов, которые не только способствовали бы повышению анодной стойкости свинца, но и удовлетворяли бы требования технологии в случае, если ионы этих элементов будут поступать с анода в раствор и оказывать воздействие как на катодный, так и на анодный процессы [1–4].

Согласно другой точке зрения, стойкость свинца зависит от изменения или модифици- рования его структуры при легировании, т. е. от величины кристаллов сплава. Модификаторами структуры сплава могут служить металлы, имеющие малую межатомную связь и, следовательно, низкую температуру плавления, малую прочность и твёрдость. Адсорбируясь на зарождающихся кристаллах, они тормозят их рост, уменьшают поверхностную энергию вновь зарождающегося кристалла, в результате чего образуется высокодисперсный сплав. Таким образом, исследование физико-химических, теплофизических и термодинамических свойств сплавов свинца с щелочноземельными металлами является актуальной задачей, так как позволяет научно обосновать выбор состава двойных и многокомпонентных сплавов для различных отраслей техники, в том числе кабельной [3, 4].

Целью настоящей работы является изучение влияния добавок кальция на теплофизические свойства и термодинамические функции сплава свинца с сурьмой марки ССуЗ.

Теория метода и описание установки

Одним из методов, позволяющий корректно установить температурную зависимость теплоемкости металлов и сплавов в области высоких температур, является метод сравнения скоростей охлаждения двух образцов, исследуемого и эталонного, по закону охлаждения Ньютона – Рихмана.

Расчет теплоемкости основывается на следующих уравнениях.

Количество тепла, переданное образцом объёма dV за время dτ , равно

• 5    Q = С 0 pdTdVd т , (1) ^P d т

где С_P – удельная теплоёмкость металла; p - плотность металла; Т - температура образца (принимается одинаковая во всех точках образца, так как линейные размеры тела малы, а теплопроводность металла велика).

С другой стороны, количество тепла, переданное образцом за отрезок времени d τ в окружающую среду, можно вычислить по закону

5 Q = a (T - T _o) dSd т , (2) где а - коэффициент теплоотдачи, зависящий от состояния поверхности образца; Т – температура поверхности; Т ₀ – температура окружающей среды; S – площадь поверхности всего образца.

Приравнивая выражения (1) и (2), получим

С 0 p—dV = a (T - T ) dS .            (3)

^Р d т               ⁰

Здесь

dT d т

скорость охлаждения, показы- вающая, как быстро меняется температура остывающего образца со временем, т. е. изме- няется его температура за единицу времени.

Количество тепла, которое теряет весь объём образца, равно

Q = J С0 pdTdV = / a (T - T o )dS ,      (4)

v     d т      S

dT

Полагая, что СP , p и не зависят от d т координат точек объема, а a, T и T0 не зависят от координат точек поверхности образца, можно записать

СРpVdT = а ( T - T o) S , d т

или

С 0 mdT = а (T - T_o ) S , ^Р d т           ^o

где V – объем всего образца, а ρ V = m – масса.

Соотношение (6) для двух образцов одинакового размера при допущении, что S 1 = S 2 ,

T 1 = T 2 , α 1 = α 2 , запишется так:

P 1

P 2

m ₁

m ₂

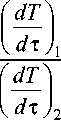
где m1 = ρ1V1 – масса эталона; m2 = ρ2V2 – масса исследуемого образца;

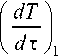
dT ^ d ^тР ₂

скорости охлаждения эталона и изучаемых образцов при данной температуре.

Для определения теплоемкости строятся кривые охлаждения исследуемых образцов и эталона (Cu). Кривая охлаждения представляет собой зависимость температуры образца от времени при охлаждении его в неподвижном воздухе.

Тройные сплавы, т. е. сплав ССу3 с кальцием, получали в шахтной лабораторной печи сопротивления типа СШОЛ при температуре 650–700 °С. Содержание кальция в сплавах варьировалось в передах 0,01–0,5 мас. %. Из полученных сплавов отливались цилиндрические образцы диаметром 16 мм, длиной 30 мм в графитовую изложницу заданной фор- мы для исследования теплоемкости. Содержание кальция в сплавах определяли гравиметрическим методом путём перевода его в оксалатную.

Измерение теплоемкости проводилось на установке, схема которой представлена на рис. 1. Установка состоит из следующих узлов: электропечь 3 смонтирована на стойке 6 , по которой она может перемещаться вверх и вниз (стрелкой показано направление перемещения). Образец 4 и эталон 5 (тоже могут перемещаться) представляют собой цилиндр длиной 30 мм и диаметром 16 мм с высверленными каналами с одного конца, в которые вставлены термопары 4 и 5 . Концы термопар подведены к цифровому многоканальному термометру 7 , который подсоединен к компьютеру 8 .

Включаем электропечь 3 через автотрансформатор 1 , установив нужную температуру с помощью терморегулятора 2 . По показаниям цифрового многоканального термометра 7 отмечаем значение начальной температуры. Вдвигаем измеряемый образец 4 и эталон 5 в электропечь 3 и нагреваем до нужной температуры, контролируя температуру по показаниям цифрового многоканального термометра на компьютере 8 . Далее измеряемый образец 4

и эталон 5 одновременно выдвигаем из электропечи 3 . С этого момента фиксируем снижение температуры. Записываем показания цифрового термометра 7 на компьютере 8 через фиксированное время (от 0,1 до 20 с). Охлаждаем образец и эталон ниже 30 °С.

Теплоёмкость сплава ССу3 с кальцием измеряли в режиме «охлаждения» по методикам, описанным в работах [5–16]. Обработка результатов измерений и построение графиков производилось с помощью программ MS Excel и Sigma Plot. Значения коэффициента корреляции ^ _корр >  0,998 , что подтверждает правильность выбора аппроксимирующей функции. Временной интервал фиксации температуры составлял 10 с. Относительная ошибка измерения температуры в интервале от 40 до 400 °С составляла ±1 %, а в интервале более 400 °С – ±2,5 %. Погрешность измерения теплоемкости по предлагаемой методике не превышает 4 %.

Полученные зависимости скорости охлаждения образцов сплавов описываются уравнением вида

T = - a exp( - b т ) - p exp( k т ), (8) где a , b , p , k – постоянные для данного образца, τ – время охлаждения.

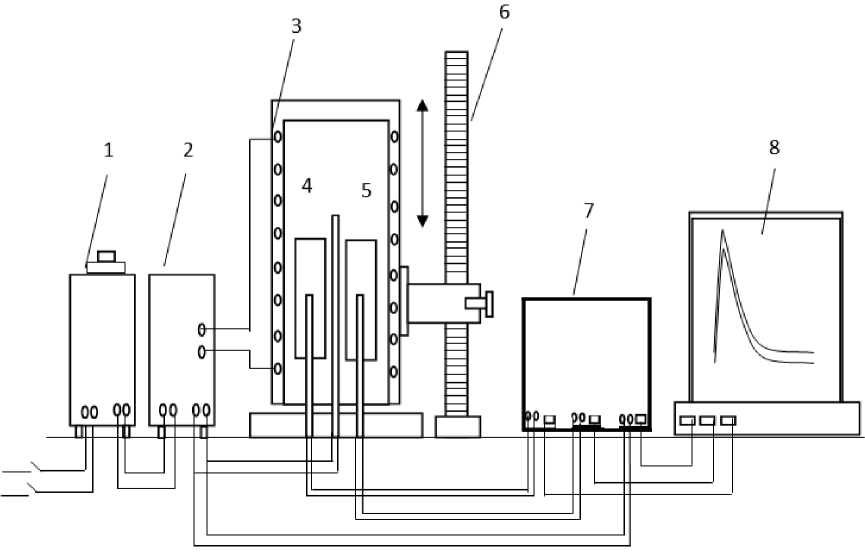
Рис. 1. Установка для определения теплоемкости твердых тел в режиме «охлаждения»: 1 – автотрансформатор; 2 – терморегулятор; 3 – электропечь; 4 – образец измеряемый; 5 – эталон; 6 – стойка электропечи; 7 – многоканальный цифровой термометр; 8 – регистрирующий прибор (компьютер). (Малый патент РТ № ТJ 877. Установка для определений теплоемкости и теплопроводности твердых тел. Приоритет изобретения от 20.04.2017)

Дифференцируя уравнение (8) по τ, получаем уравнение для определения скорости охлаждения сплавов

dT = -abe-bτ - pke-kτ. (9) dτ

По этой формуле нами были вычислены скорости охлаждения эталона и образцов из сплава ССу3 с кальцием.

Результаты и их обсуждение

Результаты исследования температуры охлаждения изучаемых сплавов представлены на рис. 2. В общем случае полученный график температуры образцов ( Т ) от времени охлаждения (τ) для образцов сплава ССу3 с кальцием имеют вид наклонных линий, которые отражают непрерывное уменьшение температуры образцов и эталона по мере их охлаждения. На кривых охлаждения термические эффекты, связанные с фазовым превращением, не обнаружены.

Обработкой кривых скорости охлаждения образцов установлены экспериментальные значения коэффициентов a , b , p , k , ab , pk уравнения (9), которые приведены в табл. 1.

Кривые скорости охлаждения сплавов представлены на рис. 3.

Расчет скорости охлаждения образцов проводился по уравнению (9).

Для определения удельной теплоемкости сплава ССу3 с кальцием использовали формулу (7). Проводя полиномную регрессию, получили следующее общее уравнение для температурной зависимости удельной теплоёмкости эталона (Cu марки М00) и сплава ССу3 с кальцием:

С_P ⁰ = a + bT + cT ² + dT ³.              (10)

Значения коэффициентов в уравнении (10) представлены в табл. 2.

На рис. 4 и в табл. 3 приведены результаты расчетов температурной зависимости

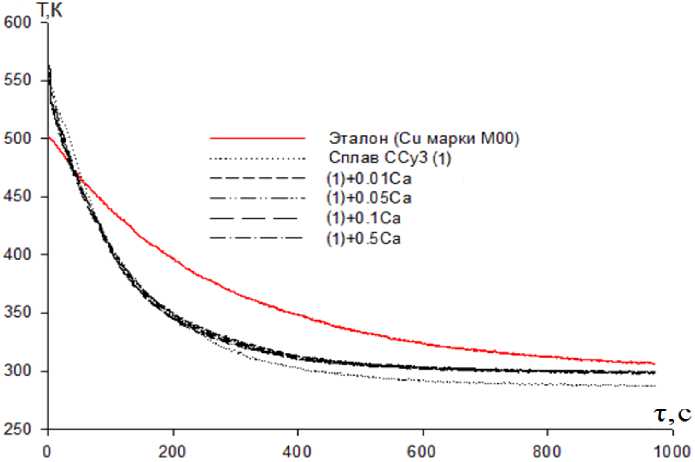
Рис. 2. График зависимости температуры ( Т ) от времени охлаждения ( τ ) для образцов из сплава ССу3 с кальцием

Таблица 1

Значения коэффициентов a , b , p , k , ab , pk в уравнении (9) для сплава ССу3 с кальцием

Содержание кальция в сплаве ССу3, мас. %	α , К	b ⋅ 10 - 3, c - 1	ρ , К	k ⋅ 10 - 5, c - 1	ab , К ⋅ c - 1	pk ⋅ 10 - 2, К ⋅ c - 1
Сплав ССу3 (1)	262,0	8,13	296,42	3,50	2,13	1,04
(1) + 0,01 Са	232,0	8,58	311,20	4,47	1,99	1,39
(1) + 0,05 Са	235,9	8,81	310,55	4,25	2,08	1,32
(1) + 0,1 Са	231,1	8,89	309,97	4,35	2,06	1,35
(1) + 0,5 Са	245,0	9,35	309,74	3,98	2,29	1,23
Эталон (Сu марки М00)	186,0	4,06	316,51	4,59	7,56	1,45

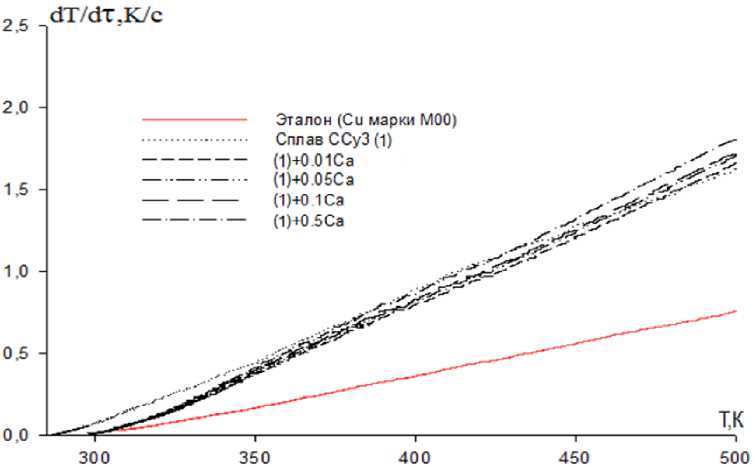
Рис. 3. Температурная зависимость скорости охлаждения образцов из эталона (Cu) и сплава ССу3 с кальцием

Таблица 2

Значения коэффициентов a , b , с , d в уравнении (10) для эталона и сплава ССу3 с кальцием

Содержание кальция в сплаве ССу3, мас. %	а , Дж/кг·К	b , Дж/кг·К2	с , Дж/кг·К3	d , Дж/кг·К4	Коэффициент корреляции R 2, %
Сплав ССу3 (1)	–3643,537	23,193	–0,044	3,07	0,9989
(1) + 0,01 Сa	–951,4588	20,700	0,0065	–8,28	0,9998
(1) + 0,05 Сa	–1200,216	3,5171	0,0038	–6,73	0,9997
(1) + 0,1 Сa	–1054,343	2,5748	0,0058	–7,93	0,9988
(1) + 0,5 Сa	–1356,691	4,5972	0,0013	–4,14	0,9999
Эталон (Сu марки М00)	324,4543	0,2751	0,000287	1,42·10–6	1,00

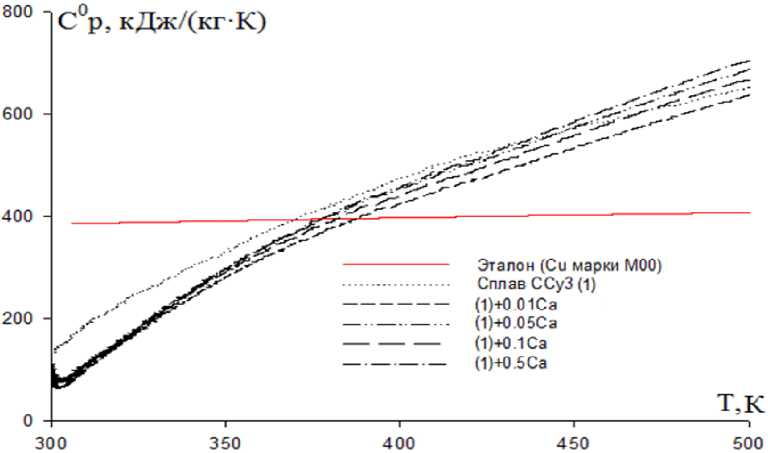
Рис. 4. Температурная зависимость удельной теплоёмкости (кДж/кг·К) эталона (Cu марки М00) и сплава ССу3 с кальцием

Таблица 3

Температурная зависимость удельной теплоёмкости (кДж/кг·К) сплава ССу3 с кальцием, эталона (Cu марки М00) и свинца С2

Содержание кальция в сплаве ССу3, мас. %	Т, К					Рост СP 0 , %
	300	350	400	450	500
Сплав ССу3 (1)	0,2043	0,3528	0,3911	0,3979	0,4539	122,17
(1) + 0,01 Са	0,1400	0,2228	0,3914	0,5299	0,6756	382,57
(1) + 0,05 Са	0,1343	0,2376	0,4160	0,5697	0,7279	441,99
(1) + 0,1 Са	0,1316	0,2355	0,4071	0,5596	0,7077	437,76
(1) + 0,5 Са	0,1290	0,2396	0,4222	0,5811	0,7414	474,73
Рост СP 0 , %	–36,86	–32,09	7,95	46,04	63,34
Эталон (Сu марки М00)	0,3859	0,3917	0,3976	0,4031	0,4081	5,74
Cu [17]	0,3839	0,3916	0,3976	0,4030	0,4079	6,25
Pb [17]	0,1275	–	0,1328	–	0,1376	7,92
Pb [18]	0,1191	0,1221	0,1284	0,1355	0,1408	18,22
Свинец (Pb марки С2) [19]	0,1191	0,1221	0,1284	0,1355	0,1408	18,22

Таблица 4

Температурная зависимость изменения термодинамических функций сплава ССу3 с кальцием и эталона (Cu марки М00)

Содержание кальция в сплаве ССу3, мас.%	[ H o ( T ) - H o ( T o * )], кДж/кг для сплавов
	Т, К
	300	350	400	450	500
Сплав ССу3 (1)	0,221741	11,53511	30,72191	55,12277	83,20707
(1) + 0,01 Сa	0,049268	6,160797	21,1717	44,37573	74,75613
(1) + 0,05 Сa	0,04574	6,509412	22,61349	47,52641	80,17774
(1) + 0,1 Сa	0,048638	6,411224	22,14334	46,47968	78,35754
(1) + 0,5 Сa	0,038968	6,481416	22,8228	48,21625	81,65963
Эталон (Cu марки М00)	0,711986	20,13154	39,8675	59,88805	80,16671
	[ SoTT ) - S o( T o * )], кДж кг^К для сплавов
Сплав ССу3 (1)	0,000841	0,038516	0,093793	0,1566	0,222494
(1) + 0,01 Сa	0,000165	0,018644	0,058477	0,112959	0,176855
(1) + 0,05 Сa	0,000153	0,019685	0,062418	0,120912	0,189583
(1) + 0,1 Сa	0,000163	0,019397	0,061144	0,118285	0,185331
(1) + 0,5 Сa	0,00013	0,019586	0,062945	0,122565	0,192898
Эталон (Cu марки М00)	–0,01033	0,049525	0,102223	0,149379	0,192105
	[ G o( T ) - G o( T o * )], кДж/кг для сплавов
Сплав ССу3 (1)	–0,03046	–1,94538	–6,79524	–15,3472	–28,0398
(1) + 0,01 Сa	–0,00015	–0,36466	–2,21910	–6,45572	–13,6714
(1) + 0,05 Сa	–0,00013	–0,38043	–2,35363	–6,88391	–14,6138
(1) + 0,1 Сa	–0,00015	–0,37775	–2,31417	–6,74843	–14,3078
(1) + 0,5 Сa	–0,00011	–0,37354	–2,35515	–6,93792	–14,7895
Эталон (Cu марки М00)	3,811822	2,797884	–1,02179	–7,33232	–15,886

* To = 298,15 К удельной теплоемкости эталона (Cu) и сплава ССу3 с кальцием через 50 К. Из рис. 4 видно, что в исследованном температурном интервале с ростом температуры теплоемкость сплава ССу3 с кальцием растёт, а у эталона (меди) изменяется незначительно. Приведённые в табл. 3 значения теплоёмкости свинца, полученные нами [19] по вышеописанной методике, хорошо согласуются с данными, представленными в справочниках [17, 18].

Используя вычисленные данные по теплоемкости сплава ССу3 с кальцием и экспе-

риментально полученные величины скорости охлаждения образцов, нами был рассчитан коэффициент теплоотдачи α( T ) (Вт/(К·м²)) для эталона (Cu) и сплава ССу3 с кальцием по следующей формуле

a =

⁰ C_P

dT d т

( T - T o ) S'

Для сплава ССу3 с кальцием температурная зависимость коэффициента теплоотдачи представлена на рис. 5.

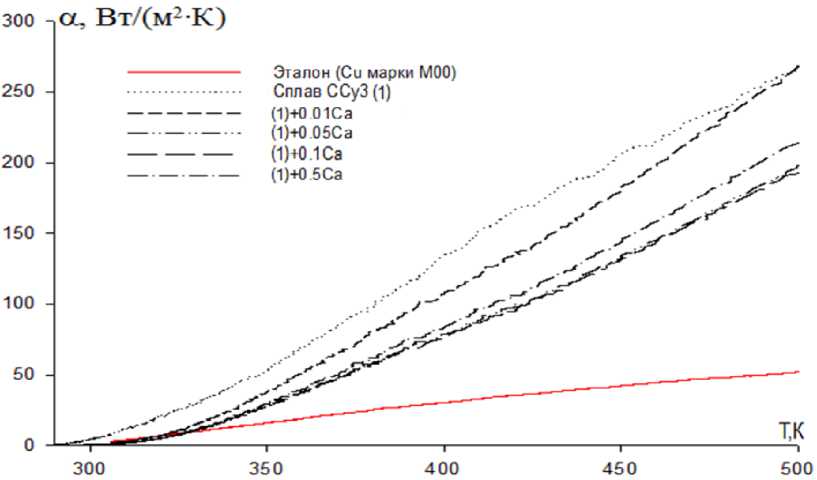
Рис. 5. Температурная зависимость коэффициента теплоотдачи эталона (Сu) и сплава ССу3 с кальцием

Для расчета температурной зависимости изменений энтальпии, энтропии и энергии Гиббса для сплава ССу3 с кальцием были использованы интегралы от удельной теплоемкости по уравнению (10):

H ^o( T ) - H ° (T₀) = a ( T - T o ) + 2( T ² - T 2) +

+ C (T — To3) + fT4 — To4);(12)

S ^o( T ) - S ^o( T o) = a In - + b (T - T o ) +

T 0

+ 2(T2 - To2) + y(T3 - To3);(13)

[ G ^o ( T ) - G ^o (298,15)] = [ H ^o ( T ) - H ^o (298,15)] -

-T [ S o(T) - S o(298,15)].(14)

Результаты расчетов температурной зависимости изменения энтальпии (кДж/кг), энтропии (кДж/кг·К) и энергии Гиббса (кДж/кг)

для эталона (Сu марки М00) и сплава ССу3 с кальцием по уравнениям (12)–(14) через 50 К представлены в табл. 4.

Заключение

Получены полиномы температурной зависимости теплоемкости и изменение термодинамических функций (энтальпия, энтропия и энергия Гиббса) для эталона (Cu марки М00) и сплава ССу3 с кальцием, которые с коэффициентом корреляции Rкорр = 0,999 описывают их изменения. Показано, что с ростом температуры удельная теплоёмкость, энтальпия и энтропия сплава ССу3 с кальцием увеличиваются, а значения энергии Гиббса уменьшаются. С ростом содержания кальция теплоемкость исходного сплава ССу3 до температуры 400 К уменьшается, далее до 500 К незначительно растёт. Указанные изменения теплоёмкости сплавов связаны с ростом сте- пени гетерогенности структуры сплава ССу3 при легировании его кальцием [20, 21].