Температурная зависимость вязкости стеклообразующих жидкостей

Вязкость является принципиально важным свойством, определяющим специфику стеклообразного состояния вещества. Стеклообразующие жидкости отличаются высокой вязкостью, которая снижает скорость кристаллизации. Представление о стекле как о сложном расплаве высокой вязкости было сформулировано еще Д.И. Менделеевым. Однако при этом до сих пор нет общепризнанного объяснения как причины резкого повышения вязкости в области стеклования жидкостей, так и природы самого перехода жидкость-стекло [1-17]. Атомный механизм вязкого течения неорганических стекол и их расплавов описан Дугласом [13], Смитом, Финлейсоном, Ремде [14], Мюллером [15] и другими авторами [1-3, 6, 16, 17].

Дырочная теория жидкостей в ее простейшей форме [18] неприменима к текучести тугоплавких стеклообразующих расплавов вследствие высокого значения у них энергии валентных связей [15]. Мюллером [15] впервые развито представление о том, что механизм вязкого течения стекол и их расплавов заключается в активационном переключении валентных связей между атомами. Эта идея получила дальнейшее развитие в валентно-конфигурационной теории Немилова [1, 19, 20]. Смит, Финлейсон и Ремде [14] предложили модель вязкого течения силикатных стекол, в которой предусматривается возможность разрыва связи Si-O и переключения связей Si-O на ненасыщенные ионы кремния и кислорода. Если мостиковый ион кислорода в мостике Si-O-Si в результате поперечных тепловых колебаний приблизится близко к ненасыщенному иону кремния, то может произойти переключение валентной связи (рис. в [14]). На рис. 1 приводится схема механизма переключения мостиковых связей Si-O-Si в силикатных стеклах по Немилову [20].

Из соотношений для коэффициента вязкого течения жидкостей наибольшее распространение получило уравнение Эйринга [1, 21]

П

Nh I ( F „ ---- I exp I —ⁿ

Vn ) I RT где Fn - свободная энергия активации процесса вязкого течения, равная изменению свободной энергии системы при изотермическом переходе из равновесного в активированное состояние, Vn - активационный объем вязкого течения, h – постоянная Планка, N – число кинетических единиц (атомов, молекул).

Для стеклообразующих жидкостей величина F _n ( T) существенно зависит от температуры, особенно в области перехода жидкость-стекло. В настоящее время нет общепризнанной формулы, выражающей явный вид функции F _n ( T).

В валентно-конфигурационной теории [1, 19, 20] свободной энергии активации текучести Fn в области размягчения стекла придается смысл флуктуационного изменения упругой энергии, при котором упругий элемент структуры превращается в вязкий элемент. Активационный объем вязкого те- чения Vn соответствует масштабу элементарного активационного смещения мостикового атома при переключении соседних мостиковых связей в направлении сдвигающего напряжения (рис. 1)

F

V = n G где G - мгновенный модуль сдвига (при комнатной температуре), Fn - свободная энергия активации текучести в области стеклования ((1))

F η = 2.3 RT g (lgη g – lg η 0 ),

n g - значение n при температуре стеклования T g , п о — предэкспоненциальный множитель в уравнении вязкости

Nh

п = — oV п

который определяется экстраполяцией кривой lg n - 1/ T к высоким температурам 1/ T =0.

В данной теории величина F _n представляется в виде суммы потенциала переключения мостиковых связей F η⁰ и потенциала конфигурационного изменения структуры вокруг места переключения связей F n k ( T) [19, 20]

F η = F η⁰ + F ηk (Т) (5)

При этом явный вид функции F _n k ( T) не раскрывается. Идея разделения свободной энергии активации текучести на две составляющие – энергию переключения связи и энергию, необходимую для из-

менения взаимных ориентаций групп атомов, – была высказана ранее Адамом и Гиббсом [22], Фили-

повичем и Калининой [23].

(а)(b)

I I I I

Si О Si            Si О Si

+ о          O          a r^z OO -

Si O Si            Si O Si

Illi

(c)

Si O Si

O          O

II

Si O Si

II

Настоящая работа посвящена анализу природы температурной зависимости вязкости стеклообразующих жидкостей в области перехода жидкость-стекло на основе сравнения уравнения Эйринга с эмпирическими соотношениями с привлечением дырочно-активационной [11, 17, 24] и валентно-конфигурационной [1, 19] теорий вязкого течения жидкостей. При этом используется новый подход к понятию о флуктуационной дырке [9, 10] (при сохранении формализма дырочно-активационной модели) [11, 18].

Эмпирические уравнения вязкости и их взаимосвязь

Неоднократно предпринимались попытки установить,

какое из существующих соотношений лучше всего описывает температурную зависимость вязкости. Меерлендер [28] в результате сравнения эмпирических уравнений вязкости с опытными данными для стеклообразующих распла-

Рис. 1. Схема переключения мостиковых связей Si – O – Si в силикатных стеклах [20]

вов и других жидкостей Енкеля [29] в виде

пришел к выводу, что уравнение

П = A exp

B

— +

T

C

_T exp

D )

T J

лучше описывает экспериментальные данные в широком интервале температуры, чем другие выра-

жения.

При сравнительно низких температурах, вблизи области стеклования, часто используются сле-

дующие соотношения Уотертона [27]:

n = По exp

Фогеля-Фулчера-Таммана [28-30]

П = A exp

/

B

T

^^^^^^^^.

T

a

_T exp

Вильямса-Ландела-Ферри [31]

ln a _T

^- C 1

T - T ^g

T - T_g + C

где a_T = n ( T)/ n (T g ) - относительная вязкость. «Двойная экспонента» типа формулы Уотертона (7) предлагалась Бредбури [32], Шишкиным [33], она подробно исследована Поспеловым [34], где показана ее оправданность в области стеклования.

При относительно низких температурах (в области стеклования), когда в квадратных скобках (6) можно пренебречь первым слагаемым в сравнении с экспонентой, уравнение Енкеля (6) переходит в соотношение Уотертона (7). Следовательно, уравнение Енкеля (6) оказывается обобщенным вариантом соотношения Уотертона (7). В свою очередь из формулы типа Уотертона-Шишкина (7) выводит-

ся уравнение Вильямса-Ландела-Ферри (9), которое эквивалентно соотношению Фогеля-Фулчера-Таммана (8) [11, с. 91].

В самом деле, для логарифма относительной вязкости из уравнения Уотертона (7) следует выражение

, a I b

In a _T = — exp I —

T g V T g

T I T - T I

—- exp I - b ------— I - 1

T I TT I

V             g 7

Если вблизи T » T g принять обозначение b ( T-T g )/ TT_g = x и при x <<1 положить

e^x = 1 + x + x , 2

1 + x = I 1

2 V

x

¹ , ТТ ^g ≈ T g² ,

то это равенство (10) переходит в уравнение Вильямса-Ландела-Ферри (9)

/

ln a _T

V

2 a ь / t I

----e ^g I —

T g | t

T - T g

- T g + (2 T g ² / b )

Легко видеть, что из уравнения Фогеля-Фулчера-Таммана выводится формула Вильямса-Ландела-Ферри и их параметры связаны следующими соотношениями [11]

C, = — 1 T ^g

B

, С 2 = T g – T 0

T

o

Таким образом, приходим к выводу о том, что выражение Енкеля (6) является наиболее предпочтительным обобщенным вариантом основных эмпирических уравнений вязкости стеклообразующих жидкостей. Поэтому представляет интерес выяснение его природы.

Сравнение уравнений Эйринга и Енкеля

Активационный объем текучести У_п, рассчитанный по формуле Немилова (2), оказывается равным объему мостиковых атомов (- O -, – S -, -Se -, – F -), ответственных за вязкое течение. Кроме того, Немиловым [1, 19] установлено, что независимо от выбранной модели предэкспоненциальный множитель в различных уравнениях вязкого течения определяется молекулярным или атомным объемом кинетических единиц, участвующих в вязком течении, а наиболее общим выражением для предэкс-поненциального множителя п о является соотношение Эйринга (4).

Поэтому естественно принять, что параметр A в соотношении Енкеля (6) совпадает с предэкспо-нентой в уравнении Эйринга

Nh

A =---

V n

Сравнение уравнений (1) и (6) при условии (11) приводит к следующей температурной зависимости свободной энергии активации вязкого течения

F = RB + RC exp I D n                       1 I T где R – газовая постоянная.

Можно убедиться, что соотношение (12) находится в согласии с экспериментальными данными для F _n ( T), полученными с помощью уравнения Эйринга (1) из опытных значений вязкости п ( Т)

F η = 2.3 RT (lgη – lg η 0 )

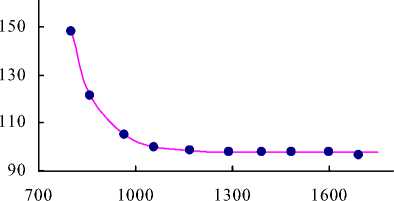
С целью получения надежных значений п о при экстраполяции кривой lg n — 1/ T к 1/ T =0 в нашей работе использован известный математический метод экстраполяции с помощью полинома Лагранжа (пункт 5). Как видно из рис. 2, свободная энергия активации текучести F _n при повышенных температурах фактически постоянна, а при понижении температуры в области стеклования резко возрастает. Путем соответствующего подбора значений параметров B , C и D с помощью соотношения (12) можно успешно описать кривую F _n ( T) на рис. 2 (пункт 5) [35]. Естественно полагать, что в формуле свободной энергии активации вязкого течения (12) второе слагаемое, которое экспоненциально зависит от температуры, отражает структурные изменения стеклообразующего расплава в процессе вязкого течения. Показатель экспоненты D , умноженный на газовую постоянную R , можно рассматривать как потенциал некоторого элементарного акта изменения структуры: e _k = RD . Низкое значение s k , например, для щелочносиликатного стекла ( D =2500 K [25])

sk = RD = 21 кДж/моль, указывает на тот факт, что элементарный акт изменения структуры при вязком течении стекол относится к низкоэнергетическим процессам.

E η , кДж/моль∙K

T, K

Рис. 2. Температурная зависимость свободной энергии активации вязкого течения расплава силикатного стекла, определенная из экспериментальных данных о вязкости по формуле (13) [15]. Содержание SiO 2 50 мол.% (образец №6 в работе [15])

При повышенных температурах RT >> ε k указанное экспоненциальное слагаемое в формуле (12) обращается в нуль и свободная энергия активации вязкого течения определяется первым слагаемым, которое практически не зависит от температуры (рис. 2)

F η (Т → ∞) = F η⁰ ≅ const = RB .

Следовательно, величина RB представляет собой предельное значение F η при T →∞. Оценка F η⁰ по этой формуле для щелочносиликатного стекла ( B =13226 K [25])

Fη0 = RB = 110 кДж/моль согласуется с предельными значениями свободной энергии активации вязкого течения силикатных стекол при повышенных температурах (рис. 2):

F η⁰ = 90-125 кДж/моль [15].

Постоянство F _η = F _η ⁰ ≅ const означает, что при высоких температурах ( T >> D ) стеклообразующий расплав ведет себя как простая жидкость типа расплавов металлов с постоянной свободной энергией активации. Следовательно, наличие второго слагаемого в формуле (12) для зависимости F η ( T ) характерно для стеклообразующих жидкостей.

На основе сравнения соотношения валентно-конфигурационной теории (5) с зависимостью (12) можно полагать, что потенциал локального конфигурационного изменения структуры F η k с большой вероятностью экспоненциально зависит от температуры

F ηk = RC exp (D/T),                                        (15)

а потенциал переключения мостиковых связей E η⁰ соответствует пределу свободной энергии активации E η⁰ = RB при T → ∞.

С этих позиций низкое значение ε k = RD (14) в соотношении (15) свидетельствует о том, что элементарный акт конфигурационного изменения структуры вокруг места переключения валентных связей является низкоактивационным процессом.

Дырочно-активационная модель и уравнение Енкеля

Обращается внимание на тот факт, что потенциал элементарного акта изменения структуры в процессе вязкого течения щелочносиликатного стекла ε k = RD (14) по величине совпадает с энергией образования флуктуационной дырки ε h в силикатных стеклах, определенной по формуле дырочной модели жидкостей и стекол [11]

ε h = RT g ln(1/f g ) ≈ 20-23кДж/моль,                                 (16)

где f_g – доля флуктуационного свободного объема, замороженная при T_g .

Это наводит на мысль о том, что хотя «дыркообразование с обрывами валентных связей не может служить механизмом процесса текучести» тугоплавких стеклообразующих расплавов [15], процессы образования и исчезновения флуктуационных дырок могут играть важную роль в локальных низкоэнергетических изменениях структуры, подготавливающих необходимое условие для переключения (или разрыва) межатомных связей.

По Мюллеру [2], переключению валентных связей предшествует низкоактивационное растяжение структурной сетки, которое тесно связано с возбуждением колебаний валентных связей. После дос- тижения некоторого критического растяжения сетки наступает взаимодействие вращательно колеблющихся возбужденных валентных связей. Средняя энергия возбуждения валентных колебаний в силикатных стеклах, по Мюллеру [15], составляет около eV® 20 кДж/моль (5 ккал/моль), что совпадает с энергией образования флуктуационной дырки eh. По-видимому, «дыркообразование» соответствует процессу возбуждения валентных колебаний, которые приводят к критической локальной деформации структурной сетки.

Ранее нами была предложена интерпретация понятия о флуктуационных дырках в жидкостях и стеклах, согласно которой «образование флуктуационной дырки» соответствует локальной предельной деформации межатомной связи, обусловленной критическим смещением (возбуждением) мостикового атома [9, 10]. Они не имеют никакого отношения к геометрическим микропустотам между атомами и молекулами, а характеризуют динамику локальных структурных изменений в аморфных средах.

В терминах формализма дырочно-активационной модели [11, 17, 24] ниже рассматривается обоснование уравнения Енкеля (6). Под понятием «образование дырки» подразумевается указанный выше его физический смысл [10]. С учетом данного замечания проводится обсуждение полученных результатов (пункт 7).

Френкелем [36], Маседо и Литовицем [37] развито представление о том, что вероятность перехода W кинетической единицы из одного положения в другое (молекулярная подвижность в жидкостях) определяется двумя независимыми факторами: вероятностью W1 образования дырки у данной частицы и вероятностью W2 того, что частица имеет энергию U∞, необходимую для перескока в соседнюю дырку,

W = W 1 W 2                                             (17)

При высоких температурах, как правило, в жидкостях всегда имеется достаточное количество ды рок (Wi~1), так что молекулярная подвижность определяется главным образом вероятностью пере- скока частицы в «готовую микропустоту»

( U

W , = exp - —^:

² V kT

С понижением температуры структура жидкости уплотняется (уменьшается количество дырок) и в подвижности молекул существенную роль начинает играть дефицит дырок – вероятность образования дырки (локального разрыхления структуры), которая по Коену и Тернбулу [38] выражается сле- дующим соотношением

W 1 = exp

- ^Y

V v f 7

где v o – минимальный объем дырки, куда может перескочить молекула, v f = V f / N – средний флуктуационный свободный объем, приходящийся на одну частицу, у - фактор перекрывания микропустот (0.5 <  у < 1).

Под «вероятностью образования дырки» W1, по нашему мнению, следует понимать в более широ- ком смысле вероятность локального изменения структуры, которое, в свою очередь, определяется процессом возбуждения мостикового атома (пункт 7). Однако здесь сохраняем термины и формализм дырочно-активационной модели [11, 24]. В равенстве (19) раскроем явный вид температурной зависимости флуктуационного свободного объема vf (T). С этой целью рассмотрим зависимость концентрации дырок Nh/N от температуры.

Будем полагать, что общее число узлов в решетке как занятых, так и вакантных, равно N + N h . Конфигурационная энтропия перемешивания дырок по возможным для них узлам определяется выражением [11, 18]

S = k ln ' N ⁺ N h ) N ! N h !

Та часть термодинамического потенциала Φ , которая обусловлена присутствием дырок, записывается в виде

Ф = N h £ - IS , e = e h - IS + v h p , (20) где e , e h , 5 , v_h - изменения термодинамического потенциала, энергии, энтропии и объема жидкости, обусловленные изменениями в структуре и динамике молекулярного движения в жидкости в целом, вызванными образованием дырки. Здесь s учитывает все прочие изменения энтропии жидкости, которые не входят в конфигурационную энтропию, отражающую лишь различные возможности размещения дырок.

Требуя минимума Ф в состоянии термодинамического равновесия между актами образования и

исчезновения дырок, из условия

dФ = ^{д Ф} dN = 0 d N h     h

с учетом приведенных выше соотношений можно прийти к следующей температурной зависимости

концентрации дырок

N h =      1

N e ^e / ^kT - 1

В данной модели важную роль играет флуктуационный свободный объем V f = v h N h , доля которого определяется главным образом концентрацией дырок N h / N

f = V f = ^Vh f N A ^J V v I N

, f = V f exp

^e h kT

- 1

-1

где v=V / N – объем, приходящийся на кинетическую единицу. Для упрощения при переходе к равенству (22) термодинамический потенциал процесса образования дырки e в выражении (21) заменили энергией образования дырки e h , ибо при атмосферном давлении p = const ® 1ат в формуле (20) можно принять e h >>  v_hP [11] и, кроме того, считать, что степень неупорядоченности структуры жидкости при образовании дырки существенно не меняется: s ® 0.

В формуле (19) показатель экспоненты связан с долей флуктуационного свободного объема f v v /v v 1

Y -°- = 7 o = Y — —, v v /v v f ff откуда с учетом (22) температурная зависимость W1 (19) выражается «двойной экспонентой»

W , = exp

v

Y -^ exp

I ^v h L

Используя известную связь между n и W [36, 37]

^e h kT

- 1

n

~

W

W 1 W 2

из соотношений (17), (18) и (23) приходим к следующему уравнению вязкости

U

v

n = П о ^e xp j kT    Y VT L exp

^ ^ I - 1 kT )

,

где коэффициент пропорциональности п _о будем полагать равным предэкспоненте в уравнении Эйринга (4): П о = Nh / V ^

Это выражение (24) фактически совпадает с эмпирическим уравнением Енкеля (6) и постоянные этого уравнения оказываются связанными с параметрами дырочно-активационной модели вязкого течения в виде

B = UJR,(25)

D = eh/R,(26)

C = y f VjL-1T

I V h )

A = N h / V η

Здесь постоянная Больцмана k заменена на газовую постоянную R , тем самым величины U „ и e h отнесены к одному молю.

Важно отметить, что, как и следовало ожидать, параметр уравнения Енкеля RD имеет смысл энергии образования флуктуационной дырки e _h (26). Величина e _h = RD , рассчитанная по формуле (26) из данных о постоянной уравнения Енкеля D , находится в согласии с результатом расчета e _h по соотношению дырочной модели ((14) и (16)).

Таким образом, два независимых способа расчета e _h приводят к одинаковым результатам, что, в свою очередь, служит одним из аргументов совпадения уравнений вязкости дырочно-активационной модели (24) и Енкеля (6).

Свободная энергия активации текучести

Из сравнения полученного выражения вязкости (24) с уравнением Эйринга (1) приходим к следующей температурной зависимости свободной энергии активации вязкого течения

F n = U

+ Y vo- I kT j exp I I - 1 l Vh ) l l kT )

которая фактически совпадает с эмпирической зависимостью (12).

При T →∞ второе слагаемое в этом равенстве обращается в нуль, откуда следует, что величина U ∞ имеет смысл свободной энергии активации при T →∞

U „ = F n ( T ^ » ) = F n⁰ .

Как отмечалось выше, оценка U ∞ = RB по формуле (25) из данных о постоянной уравнения Енкеля для щелочносиликатного стекла согласуется с предельными значениями свободной энергии активации силикатных стекол при повышенных температурах F _η ⁰ [15].

Величина F _n ( T) может быть представлена в виде суммы двух слагаемых

F n = U . + U s ( Т) ,                                                   (29)

где U_∞ будем называть потенциалом перескока частицы в дырку, а U_s ( T ) – потенциалом локального изменения структуры, который является функцией температуры:

Us (T )= I Y v I kT Г exp f £,1 - 1 l v.) L lkT )

По-видимому, объемы v_o и v h по величине и смыслу близки: v_o / v h ~ 1 ( v_o - объем дырки, куда может перескочить частица, а v h – изменение объема аморфной среды, вызванное образованием дырки (20)). Среднее значение коэффициента перекрытия дырок можно принять равным около y = 0.7 (0.5 <  y < 1). Тогда коэффициент в круглых скобках в соотношении (28) равен

Y v ~ 0.7 v_h

В таком приближении полуэмпирическая формула (28) для свободной энергии активации вязкого течения содержит два подгоночных параметра £ и U„

I ^£k I , exp I I - 1

F „ = U „ + 0.7 kT

На рисунках 3-6 приводится зависимость F _n ( T) для ряда расплавов стекол. Точки представляют собой экспериментальные значения F _n ( T), полученные из данных о вязкости по формуле (13), а сплошные линии отражают результаты расчета F _n ( T) по формуле (32) при соответствующих значениях £ и U „ , которые подобраны так, чтобы расчетная кривая легла на экспериментальные точки (табл. 1). Примечательно то, что подобранные при таком условии значения £ согласуются с результатами вычисления £ по независимой формуле (16). В таблице 1 в последнем столбце приводятся значения £ , полученные с помощью соотношения (16), а в третьем столбце - подобранные величины £ . Как видно из таблицы 1, наблюдается удовлетворительное согласие между ними. Варьирование коэффициента ( y v_o / v h ) в равенстве (28) в пределах от 0.5 до 1 вместо постоянного значения 0.7 не меняет существенно полученные результаты (табл. 2).

Таким образом, температурная зависимость свободной энергии активации вязкого течения стеклообразующих расплавов (28), основанная на дырочно-активационной модели, соответствует экспериментально наблюдаемой закономерности.

Дырочно-активационная модель и валентно-конфигурационная теория вязкого течения

Естественно ожидать определенную взаимосвязь между параметрами указанных выше теорий, в частности, между объемом дырки v h и активационным объемом вязкого течения V η , который в валентно-конфигурационной теории определяется по формуле Немилова (2), а величина v_h – по соотношению [11, 39]

= 3 ( 1 - 2 ц ) RT g = RT g                                         (33)

v*         f E         f Вт g         gT где ц - коэффициент Пуассона, E - модуль упругости при одноосной деформации, BT - упругий модуль всестороннего сжатия.

В самом деле, как видно из табл. 3-6, между этими величинами наблюдается приближенная линейная корреляция

υ h /V η ≈ const ≈ 0.6-0.8                                                 (34)

Постоянство данного отношения лучше выполняется у стекол одного структурного типа с одинаковыми коэффициентами Пуассона ц = const .

Действительно, легко убедиться, что отношение объема флуктуационной дырки к активационному объему вязкого течения тесно связано с коэффициентом Пуассона. Согласно равенствам (2) и (33), отношение этих объемов зависит главным образом от упругих модулей vh

V п

RT g ] G f F J B т

,

J g п / T ибо множитель (RTg/F^) оказывается близким к единице [11, с. 114]

RT g

« 1

fF

J g п

Здесь F _n =F^g ) - свободная энергия активации вязкого течения при температуре стеклования, которая рассчитывается из данных о вязкости по формуле (3).

Таблица 1

Характеристики вязкого течения неорганических стекол R 2 O-SiO 2 (R = Li, Na, K), PbO–SiO 2 , Na 2 O– GeO 2 и Na 2 O–B 2 O 3

R 2 O, PbO, мол.%	T g , K	ε h	U ∞	F η ( T g )	- lg( η 0 , П)	f g	v h / v	εh , кДж/моль (16)
		кДж/моль
Li 2 O	Li 2 O – SiO 2
10	814	21.8	135	245	2.55	0.028	-	24.2
14	788	21	130	237	2.57	0.028	-	23.4
25	738	20.8	100	219	2.41	0.028	0.72	22.0
30	721	20.7	87	212	2.25	0.028	0.6	21.4
33.3	708	20.8	78	208	2.23	0.028	0.64	21.1
Na 2 O	Na 2 O – SiO 2
15	783	21.5	124	235	2.53	0.028	0.55	23.3
20	759	21.1	109	225	2.35	0.028	0.58	22.6
25	739	21	100	219	2.36	0.028	-	23.0
30	721	20.8	91	214	2.36	0.028	0.46	21.5
33	712	20.5	84	209	2.26	0.028	0.51	21.2
K 2 O	K 2 O – SiO 2
13	795	21.5	127	235	2.33	0.028	0.57	23.7
15	793	21	125	232	2.31	0.028	0.59	23.6
20	759	21.2	105	222	2.14	0.025	0.54	23.3
25	739	21	97	217	2.22	0.025	0.47	22.7
PbO	PbO – SiO 2
25	785	22.7	110	245	3.15	0.027	0.58	23.6
30	761	23	87	234	2.95	0.027	0.76	22.9
45	696	21	68	218	3.34	0.027	0.65	20.9
50	674	21	53	212	3.33	0.027	0.56	20.2
55	654	20.5	51	213	3.91	0.026	0.62	19.9
Na 2 O	Na 2 O – Ge 2 O
5	847	24.5	120	284	4.36	0.025	0.69	26.0
15	801	24.5	90	259	3.81	0.026	0.59	24.3
20	773	23.7	69	241	3.21	0.027	0.55	23.2
25	749	23	62	232	3.1	0.027	0.54	22.5
30	727	22.8	51	225	3.12	0.027	0.52	21.9
Na 2 O	Na 2 O – B 2 O 3
10	618	19	56	194	3.45	0.026	0.83	18.8
15	680	21.2	57	221	3.93	0.026	0.82	20.7
20	727	23.2	40	229	3.41	0.026	0.81	22.1
25	735	24.1	26	237	3.77	0.026	0.82	22.3
30	748	25	15	250	4.45	0.025	0.86	23.0

Таблица 2

О влиянии изменения коэффициента γ( v 0 / v h ) на результаты расчета для стекла Na 2 O–SiO 2 (содержание Na 2 O 15 мол. %)

γ( v 0 / v h )	ε h	U ∞	F η ( T g )	- lg( η 0 , П)
	кДж/моль
1	20	118	235	2.533
0.7	22	124	235	2.533
0.6	22	129	235	2.533
0.5	23	132	235	2.533

Следовательно, согласно известной взаимосвязи упругих постоянных в теории упругости, отношение vh/ Vn является фактически однозначной функцией коэффициента Пуассона vh ~ G                                         (35)

V п Вт v^ « 3 Г 1^2^).                            (36)

Vn   2 I 1 + М )

Оценка по этому соотношению (36) находится в согласии с экспериментальными данными. Так, подстановка типичных значений ц = 0.20-0.25 для стекол (табл. 3-6) в равенство (36) приводит к значениям v h / V _n = 0.6-0.8, что совпадает с опытными данными (34) (табл. 3-6). У щелочносиликатных стекол с ростом коэффициента Пуассона в ряду Li-Na-K отношение v h / V _n уменьшается (табл. 3), что соответствует выражению (36). Уменьшение v h / V _n у натриевогерманатных стекол при росте содержания Na₂O находится также в согласии с ростом коэффициента Пуассона (табл. 4).

Небольшая разница между величинами vh и Vn объясняется, по всей вероятности, тем, что объем дырки vh относится к случаю всестороннего сжатия, а Vn - деформации сдвига. В самом деле, как видно из равенства (35), величина vh/Vn равна отношению модуля сдвига к модулю объемного сжатия G/BT. Наряду с корреляцией между vh и Vn наблюдается линейная связь между энергией образования флуктуационной дырки eh и свободной энергией активации вязкого течения вблизи температуры стеклования Fn = Fn(Tg) (табл. 3-6)

e h / F _n = const ~ 0.08-0.09,                                       (37)

где величины e h и F _n рассчитаны соответственно с помощью формул (16) и (3).

Существование такой корреляции можно пояснить следующим образом. При низких температу- рах, вблизи T%Tg, единицей в квадратных скобках в формуле (30) можно пренебречь в сравнении с экспонентой, а также принять Yvo/vh)«1,

U s ( T g ) = kT g exp

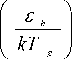
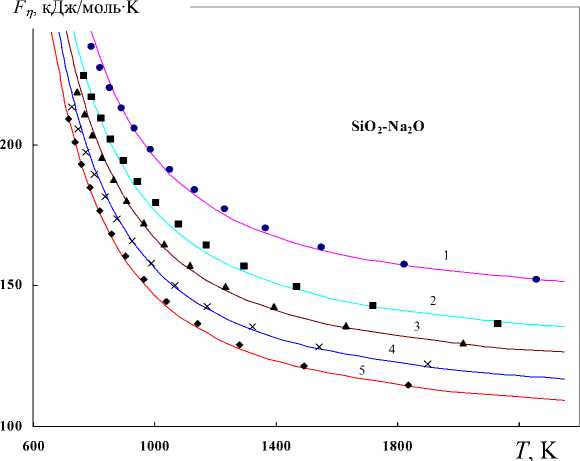
Рис. 3. Температурная зависимость свободной энергии активации вязкого течения натриевосиликатных стекол Na2O–SiO2. Точки – экспериментальные данные, кривые – расчет по уравнению (32). Содержание Na2O, мол.%: 1 – 15, 2 – 20, 4 – 30, 5 – 33

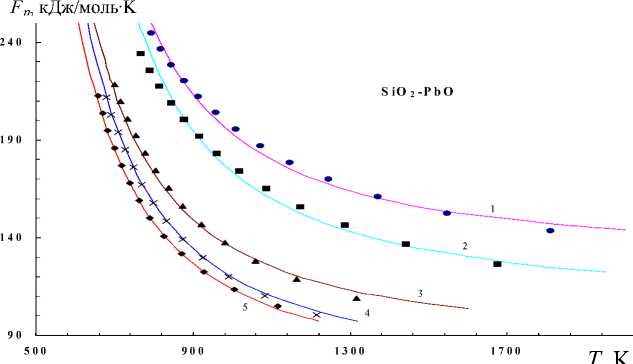
Рис. 4. Зависимость F η ( T ) для свинцовосиликатных стекол. Содержание PbO, мол.%:

1 – 24.6, 2 – 30, 3 – 45, 4 – 50, 5 – 55

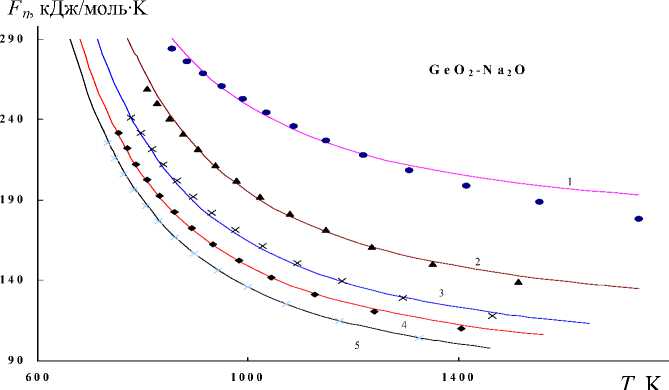
Рис. 5. Зависимость F_η ( T ) для натриевогерманатных стекол. Содержание Na₂O, мол.%:

1 – 10, 2 – 15, 3 – 20, 4 – 25, 5 – 30

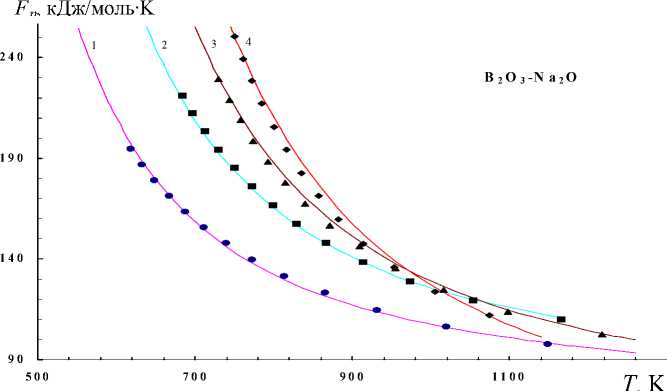
Рис. 6. Зависимость F η ( T ) для натриевоборатных стекол. Содержание Na 2 O, мол.%:

1 – 10, 2 – 15, 3 – 20, 4 – 30

Принимая во внимание (16), это равенство легко привести к следующему виду

—^h ---= f In ( 1 / f ) .

U s ( T g ) ^{g            g}

При понижении температуры в области стеклования потенциал локального изменения структуры U s ( T ) резко (экспоненциально) возрастает и становится значительно больше первого слагаемого в равенстве (29): U s ( T g )>> U „ , так что при T = T g величина F _n практически совпадает с U s

F* T g ) = U s (T g ) .

Это означает, что уравнение Енкеля (6) переходит в соотношение Уотертона (7).

Заменив в выражении (38) величину Us(Tg) на Fn(Tg), приходим к выводу, что отношение eh к Fn в области стеклования является постоянным еь/Fn = fg ln(1/fg) ~ const ~ 0.09,                                         (39)

где принято среднее «универсальное» значение f g = 0.025 [11, 31] (табл. 3-6). Оценка (39) согласуется с экспериментальными данными (37) (табл. 3-6).

При повышенных температурах в определенном интервале kT>> e _h ( T>>T g ) выражение в квадратных скобках равенства (30) равно e h / kT , ибо exp ( e h / kT) = 1+( e _h / kT), откуда потенциал локального изменения структуры при у ( v o / v h ) « 1 совпадает с энергией образования флуктуационной дырки

U s ( T >>  T g ) - е ь .

Из выражения (38) следует, что величина U , ( T g ) в области стеклования в Z . « 10 раз превышает его значение U , « e _h при повышенных температурах (40)

U,^(T, ) =

/

V

I e= Z e« 10 e f. In (1/f, )J ‘      ' ‘         *

где учтено, что f g ln (1 f g ) « const « 0.1 [11]. По-видимому, величину Z = [ / ln(1/f)] "1

можно рассматривать как число частиц или структурных единиц, вовлекаемых в перегруппировку молекул при локальном изменении структуры: Z . « 10 вблизи T . , а при T>>T . , где кинетические единицы движутся фактически свободно, имеем Z « 1 (40)).

Таблица 3

Параметры дырочно-активационной модели и валентно-конфигурационной теории щелочно-силикатных стекол R 2 O – SiO 2 (R = Li, Na, K)

R2O, мол.%	E, ГПа	μ	T g , К	- lg( η 0 , П)	f g	v h , Å3	V η , Å3	v h V η	εh , кДж/моль	F η , кДж/моль	ε h F η
Li 2 O	Li 2 O-SiO 2
10	70.8	0.187	814	2.552	0.027	6.53	9.12	0.72	24.3	273.3	0.09
14	71.9	0.153	788	2.568	0.027	6.88	8.73	0.79	23.5	264.7	0.09
25	75.0	0.223	738	2.408	0.027	4.90	7.87	0.62	21.9	245.7	0.09
30	76.4	0.235	720	2.248	0.027	4.47	7.51	0.60	21.4	237.7	0.09
33.3	77.3	0.232	709	2.236	0.028	4.38	7.33	0.60	21.1	234.0	0.09
40	79.2	0.236	689	2.166	0.028	4.07	6.98	0.58	20.4	226.4	0.09
45	80.6	0.24	675	2.330	0.028	3.84	6.82	0.56	20.0	223.7	0.09
Na 2 O	Na 2 O-SiO 2
15	62.4	0.18	782	2.533	0.028	7.10	9.95	0.71	23	262	0.09
20	60.6	0.20	758	2.347	0.028	6.61	9.88	0.67	23	252	0.09
25	58.7	0.22	738	2.360	0.028	6.25	9.98	0.63	22	245	0.09
30	56.9	0.23	721	2.357	0.028	5.89	10.1	0.58	21	239	0.09
33	55.7	0.24	711	2.262	0.028	5.62	10.1	0.55	21	235	0.09
35	55.1	0.24	705	2.233	0.029	5.65	10.2	0.55	21	232	0.09
K 2 O	K 2 O-SiO 2
13	56.6	0.23	794	2.330	0.028	6.69	11.1	0.60	23.5	263.4	0.09
15	54.9	0.225	783	2.314	0.028	6.92	11.3	0.61	23.2	259.4	0.09
20	50.6	0.25	759	2.140	0.028	6.60	11.8	0.56	22.4	248.8	0.09
25	46.2	0.27	739	2.216	0.028	6.47	12.7	0.51	21.8	243.3	0.09

Таблица 4

Параметры дырочно-активационной модели и валентно-конфигурационной теории натриевогерманатных стекол Na 2 O-GeO 2

Na 2 O, мол.%	E , ГПа	μ	т g , К	f g	v h , Å3	V η , Å3	v h V η	ε h , кДж/моль	Fη , кДж/моль	ε h F η	lg η 0
5	48.7	0.23	847	0.022	10.5	15.1	0.69	27	314	0.09	-4.35
10	50.3	0.25	831	0.022	9.4	14.4	0.65	26	306	0.09	-4.23
15	53.8	0.26	801	0.023	7.6	12.8	0.59	25	288	0.09	-3.8
20	54.9	0.265	773	0.025	6.6	11.8	0.55	24	269	0.09	-3.21
25	54.5	0.269	748	0.025	6.3	11.5	0.54	23	259	0.09	-3.1
30	53	0.273	727	0.025	6.1	11.6	0.52	22	252	0.09	-3.12

Таблица 5

Параметры дырочно-активационной модели и валентно-конфигурационной теории для стекол системы Na 2 O-SiO 2 -GeO 2

Na 2 O	SiO 2	GeO 2	E , ГПа	μ	т g , К	f g	v h , Å3	V η , Å3	v h V η	ε h , кДж/моль	Fη , кДж/моль	ε h Fη	lg η 0
мол. %
7.17	6.95	85.87	70.5	0.21	822	0.023	7.4	10.5	0.70	25.9	296	0.08	-3.84
6.78	12.11	81.11	70.4	0.24	832	0.023	6.5	10.7	0.60	26.0	304	0.08	-4.07
6.55	15.04	78.41	70.3	0.227	841	0.024	6.8	10.4	0.65	26.1	297	0.08	-3.49
6.11	20.75	73.14	69.8	0.223	845	0.024	7	10.5	0.66	26.2	300	0.08	-3.56
5.81	24.68	69.52	69.2	0.215	847	0.024	7.2	10.5	0.68	26.3	298	0.08	-3.39
5.58	27.57	66.85	68.1	0.218	849	0.024	7.3	10.9	0.67	26.4	303	0.08	-3.66

Таблица 6

Параметры дырочно-активационной модели и валентно-конфигурационной теории для стекол системы B2O3-Na2O

B 2 O 3 , мол.%	E , ГПа	μ	т g , К	f g	v h , Å 3	V η , Å 3	v h V η	εh , кДж/моль	Fη , кДж / моль	ε h F η	lg η 0
90	29.04	0.280	614	0.024	15.9	19.1	0.83	19	216	0.09	-3.45
85	35.35	0.281	679	0.024	14.6	17.8	0.82	21.1	246	0.09	-3.93
80	41.67	0.285	726	0.024	12.7	15.7	0.81	22.4	255	0.09	-3.41
75	47.92	0.282	735	0.024	11.6	14.1	0.82	22.8	264	0.09	-3.77
70	53.96	0.281	747	0.022	11.3	13.2	0.86	23.7	278	0.09	-4.45
65	56.05	0.276	750	0.020	12.1	13.1	0.92	24.3	285	0.09	-4.89
60	53.39	0.270	731	0.020	12.9	13.2	0.98	23.8	276	0.09	-4.77

Из сравнения соотношений валентно-конфигурационной теории (5) и дырочно-активационной модели (29) с учетом (30) следует, что потенциал переключения мостиковых связей Fη0 равен U∞, а по- тенциал конфигурационного изменения структуры вокруг места переключения связей Fnk совпадает с потенциалом локального изменения структуры Us(T)

F n k ( T ) = | Y — | kT I v h )

exp

s

h

kT

Таким образом, из приведенных данных следует, что дырочно-активационная модель тесно связана с валентно-конфигурационной теорией вязкого течения.

О природе основных параметров дырочно-активационной модели вязкого течения

Параметр модели U ∞ , как отмечалось выше, имеет смысл потенциала переключения мостиковых связей F η⁰ . Его можно оценить по данным о коэффициентах уравнения Вильямса-Ландела-Ферри (9) [40, с. 31] U _ю = RC 1 C 2 . Например, для листового силикатного стекла ( C 1 = 36.5, C 2 = 305 K [40, с. 32]) имеем U „ = 92 кДж/моль, что находится в согласии с приведенными выше значениями F _п ⁰ для силикатных стекол [15]. Более детального обсуждения требует природа параметров s _h и v h - природа «дыркообразования» в стеклах и их расплавах.

Низкие значения энергии образования флуктуационной дырки ε _h ≈ 20-25 кДж/моль и объема дырки v h ≈ 8-12 Å ³ в силикатных и других неорганических стеклах (табл. 1-6) указывают на то, что «дыр-кообразование» в них относится к низкоэнергетическим мелкомасштабным процессам и не может быть прямо связано с разрывом или переключением валентных связей. Однако, как уже отмечалось, «образование дырки» играет важную роль в предварительной подготовке структуры для реализации переключения связей.

Известны, по крайней мере, два-три релаксационных процесса в силикатных стеклах с низкой энергией активации порядка ≈ 20 кДж/моль (5 ккал/моль). Во-первых, это первая стадия уплотнения стекол под высоким давлением и обратный процесс их термостимулируемого разуплотнения [11, 41,

42], основные закономерности которых удовлетворительно описываются в рамках дырочной модели [11, 41]. Предполагается, что уплотнение стекол под давлением обусловлено низкоактивационными процессами деформации сетки. Во-вторых, в исследованиях внутреннего трения, а также диэлектри-

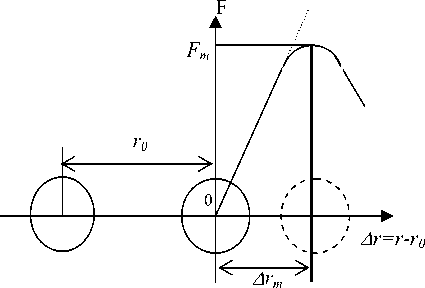
Рис. 7. Схема возбуждения атома (образования флуктуационной дырки)

ческих потерь в силикатных стеклах наблюдается релаксационный процесс с такой же низкой энергией активации ≈ 20 кДж/моль [40]. Обычно предлагаемые механизмы указанных потерь связаны с локальными деформациями кремнекислородной сетки в результате смещения мостикового атома кислорода перпендикулярно [43] или вдоль [44] направления цепочки Si-O-Si. В-третьих, процесс возбуждения валентных колебаний в силикатных стеклах, обуславливающих локальные деформации структурной сетки, характеризуется энергией активации около 20 кДж/моль [15].

Поэтому естественно полагать, что «образованию флуктуационной дырки» в стеклах и их расплавах соответствует низкоэнергетический мелкомасштабный процесс локальной деформации структурной сетки. Однако конкретный механизм и природа такой деформации сет- ки стекла остаются не совсем ясными.

Исходя из связи энергии образования дырки ε h с потенциалом конфигурационного изменения структуры вокруг места переключения связей F η k в виде (42) и из линейных корреляций между v h и V η , ε h и F η вблизи T g (табл. 3-6), можно предположить, что «процесс образования дырки» в силикатном стекле представляет собой критическое смещение мостикового атома кислорода Δ r m в структурном фрагменте Si-O-Si перед переключением соседних валентных связей (рис. 1). Линейный размер «дырки» в силикатных стеклах ν h^1/3 ≈ 1.5-2 Å (табл. 3) по порядку величины близок к масштабу критического смещения мостикового атома кислорода Δ r m (рис. 1).

Критическое смещение мостикового атома кислорода перед переключением валентных связей (рис. 1) – «дыркообразование» – можно рассматривать как процесс возбуждения атома или межатомной валентной связи, обуславливающий локальную предельную деформацию кремнекислородной сетки [2, 10]. С этой точки зрения «образование флуктуационной дырки» представляет собой предельную упругую деформацию межатомной или межмолекулярной связи Δ r m , соответствующую максимуму квазиупругой силы (рис. 7). Такой элементарный процесс можно интерпретировать по-другому: как критическое смещение кинетической единицы (атома, группы атомов) на предельное расстояние Δ r m , соответствующее максимуму силы межатомного притяжения F m (рис. 7). Кинетическая единица, способная к критическому смещению, названа возбужденным атомом, а сам подход – моделью возбужденного состояния [9, 10].

Рождение возбужденного мостикового атома – «дырки» – обусловлено флуктуационной перегруппировкой соседних частиц и носит энтропийный характер [45]. Из приведенных выше данных следует, что среднее число структурных единиц, вовлекаемых в локальную перегруппировку молекул, вблизи T_g составляет около Z_g ≈ 10 (41)). В связи с этим отметим работу [46], где методом молекулярной динамики показано, что перед разрывом межатомной связи возникает флуктуация плотности и энергии, охватывающая около десяти атомов или молекул ( Z ≈ 10) и характеризующаяся деформацией растяжения связей и коррелированным характером движения частиц в области флуктуации.

Таким образом, параметры дырочно-активационной модели вязкого течения ε h и v h входят в формулу (30) для потенциала локального изменения структуры U s ( T ) и характеризуют локальную предельную упругую деформацию структурной сетки стекла и его расплава. Они практически не имеют никакого отношения к обычным геометрическим микропустотам структуры.

Заключение

Если для простых жидкостей, например, типа спиртов с водородными связями, процесс образования флуктуационной дырки представляет собой непосредственно элементарный акт вязкого течения, то для тугоплавких стеклообразующих расплавов «дыркообразование» с обрывом валентных связей не может служить механизмом текучести из-за высоких значений у них энергии валентных связей. Однако низкоактивационные мелкомасштабные процессы образования и исчезновения флуктуационных дырок играют важную роль в локальных изменениях структуры, подготавливающих «почву» для основного акта текучести – переключения или разрыва валентных связей.

В силикатных стеклах «процесс образования флуктуационной дырки» представляет собой предельную локальную деформацию кремнекислородной сетки, обусловленную критическим смещением возбужденного мостикового атома кислорода в мостике Si-O-Si перед переключением соседних связей (рис. 1). В этом смысле флуктуационные дырки в стеклах и их расплавах оказываются эффективными величинами и фактически не имеют никакого отношения к традиционным геометрическим микропустотам между атомами (свободному вандерваальсову объему).

В дырочно-активационной модели свободная энергия активации вязкого течения F η может быть представлена в виде двух слагаемых: потенциала локального изменения структуры U s ( T ) и потенциала перескока кинетической единицы в дырку (переключения связей) U_∞ . При высоких температурах ( T → ∞) для реализации основного элементарного акта вязкого течения – переключения валентных связей между атомами – не требуется локальное изменение структуры: U_s ( T ) ≅ 0, ибо в этой области валентно-деформационное колебательное движение атомов достигает предельного всесторонне беспорядочного характера и имеется достаточное количество возбужденных мостиковых атомов, создающих, в свою очередь, предельно деформированные локальные участки сетки, так что переключения валентных связей происходят самопроизвольно при «готовых локальных изменениях структуры». В терминах дырочно-активационной модели это означает, что при повышенных температурах вязкое течение происходит за счет перескоков частиц в готовые дырки.

При низких температурах, в области стеклования, энергия возбуждения мостикового атома ε h становится сравнимой со средней энергией теплового молекулярного движения kT и количество возбужденных мостиковых атомов (локально деформированных участков сетки) резко уменьшается (экспоненциально exp (- ε h / kT )), поэтому для реализации переключения валентных связей требуется предварительное локальное изменение структуры. Этим объясняется резкий рост свободной энергии активации вязкого течения в области стеклования.