Температурное состояние и оценка отклонения формы сферической оболочки калибровочного космического аппарата на теневом участке околоземной орбиты

Калибровочные космические аппараты (ККА) применяют для оценки и контроля энергетического потенциала радиолокационного канала наземного комплекса мониторинга движения космических объектов [1; 2]. Распространенным вариантом геометрической формы ККА, называемого также калибровочно-юстировочным, является выполненная с высокой точностью сферическая оболочка. Аналогичную форму имеют пассивные ретрансляторы сигналов и используемые в целях калибровки и юстировки радиолокационной аппаратуры некоторые типы малоразмерных эталонных отражателей [1; 3], а также крупноразмерные надувные конструкции [4–6].

Орбиты ККА могут быть как круговыми с высотой около 1000 км, в том числе близкими к полярным, так и эллиптическими с апогеем до 2200 км [2; 3]. Основным фактором, влияющим на форму оболочки ККА, является распределение температуры по ее поверхности, зависящее от солнечного излучения и собственного излучения Земли [7; 8]. На теневом участке околоземной орбиты температурное состояние оболочки ККА наряду с собственным излучением Земли в некоторой степени может зависеть от энергии соударения с молекулами и атомами атмосферных газов и рекомбинации этих молекул [9]. На высоте 300 км над поверхностью Земли оценки плотности локальных тепловых потоков, вызванных этими процессами, не превышают 10 % от плотности потока излучения Земли, а на высоте более 350 км составляют менее 1 % [10].

Оболочку ККА выполняют из полимерной пленки толщиной несколько десятков микрометров, покрытой тонким слоем (толщиной несколько нанометров) напыленного алюминия [11].

Том 2

После вывода ККА на околоземную орбиту оболочка принимает сферическую форму путем наполнения ее газом при сравнительно невысоком давлении. При этом возможно получить сферическую оболочку достаточно большого диаметра, что характерно для современных тенденций развертывания на орбите крупногабаритных трансформируемых конструкций [12].

Для орбиты ККА с теневым участком в силу периодической смены интенсивности облучения оболочки происходит существенное изменение ее температурного состояния. Это приводит не ¹⁴8 только к периодическому изменению формы оболочки, но может повлиять на ресурс работоспособности ее материала в силу циклического термомеханического воздействия. Количественный анализ термомеханического состояния оболочки ККА может быть проведен методами математического моделирования [13], используя ее тепловую модель [9] и определяющие соотношения для безмоментной сферической оболочки [14].

Условия облучения оболочки

Интенсивность собственного излучения Земли, определяющего температурное состояние оболочки ККА на теневом участке орбиты, зависит от температуры участков поверхности Земли, влажности и температуры атмосферы и от состояния облачного покрова [15]. Плотность потока собственного излучения различных участков поверхности Земли, измеренная оптикоэлектронными приборами, установленными на орбитальной обсерватории, имеет существенный разброс и достигает значения 357 Вт/м2 [16]. Для экваториальной области Земли в летний период плотность этого потока составляет от 175 (при сплошной облачности с верхней границей на высоте 9 км) до 247 Вт/м2 при отсутствии облаков, а для участков в зоне северного полярного круга при тех же условиях от 145 до 225 Вт/м2 [17].

Среднее значение плотности потока собственного излучения Земли можно оценить из условия ее радиационного баланса по формуле [10; 15] q0 = qs (1 – αs) / 4, где qs – солнечная постоянная для среднего расстояния Земли от Солнца (по рекомендации Всемирного центра радиационного мониторинга (Давос, Швейцария) qs =1368 Вт/м2), αs – альбедо Земли (среднее значение коэффициента отражения солнечного излучения поверхностью Земли). Однако значение qs (несмотря на принятое название этой величины) не является строго постоянным. Интенсивность солнечного излучения зависит от текущего состояния поверхности Солнца и от положения Земли на ее эллиптической орбите при движении вокруг Солнца (эксцентриситет этой орбиты ≈ 0,0167). Многолетние наблюдения показали, что изме- нения солнечной активности слабо влияют на значение qs, вызывая отклонения в пределах 1 %, тогда как влияние положения Земли на ее орбите более существенно.

С изменением расстояния L от Солнца плотность потока солнечного излучения изменяется пропорционально квадрату отношения L ₀/ L , где L ₀ ≈ 1,49·10⁸ км – среднее расстояние Земли от Солнца. Поэтому даже при достаточно малом эксцентриситете орбиты Земли в перигелии q_s =1414 Вт/м², а в афелии – 1322 Вт/м² [10; 18]. В инженерных расчетах в случаях, когда увеличение может ухудшить характеристики КА или повлиять на его работоспособность, обычно принимают завышенное значение q_s (например, 1420 Вт/м² [19] и 1400 Вт/м² [20]). Для последующих числовых расчетов температурного состояния оболочки ККА примем значение q_s = 1420 Вт/м². Тогда при среднем значении α_s = 0,37 [18] из условия радиационного баланса Земли получим q ₀ ≈ 215 Вт/м².

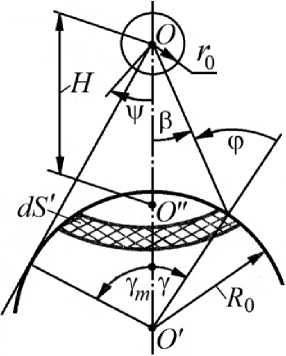
Рис. 1. Расчетная схема

При наблюдении с Земли угловой размер ККА даже при радиусе r ₀ его сферической оболочки порядка 10 м начиная с высоты H = 200 км аппарата над поверхностью Земли не превышает δ = 10^–4 рад. Поэтому при заданном значении H (расстояние между точками O и O" на рис. 1) можно считать, что на оболочку ККА падает собственное излучение Земли с участка ее поверхности, площадь которого зависит от угла

Ym = arccos(1/(1+т/)), где ƞ = H/R0, R0 ≈ 6371 км – средний радиус поверхности Земли. Выделим на этом участке поверхности кольцевой слой бесконечно малой ширины R0dγ (γ ϵ [0; γm]) площадью

dS′ = 2πR2 sin γdγ

(на рис. 1 этот слой заштрихован).

Пренебрежимо малое значение δ позволяет положить угол φ между нормалью к выделенному кольцевому слою и направлением на различные участки поверхности оболочки равным β + γ, а квадрат расстояния между этим слоем и ККА равным.

l ² = R ^!(1 + (1 + n)² -2(1 + n)cosу) .

Если принять, что распределение по отдельным направлениям излучения с поверхности Земли определяется законом Ламберта [21], то суммарный поток этого излучения, падающий на поверхность оболочки ККА, составит [9]:

Q = ^{2 n} r q о ( i^- 7 n (2 +n) / (i+n) )

Но распределение q '( у ) плотности потока этого излучения по поверхности оболочки будет неравномерным, зависящим от угла ψ , отсчитываемого от ближайшей к поверхности Земли точки на ее поверхности (рис. 1) вдоль любой дуги большого круга радиусом r 0 , проходящей через эту точку, в которой плотность потока будет равна [9] q 0 = q '(°) = q о /(1+n ^{) 2} .

С возрастанием угла у функция q'(y) убывает и в соответствии с принятым выше допущением о возможности пренебречь угловым размером оболочки примет нулевое значение при у_т = П — Y m , т. е. q' ( W m ) = 0 и, кроме того, dq '( у )/ dyI_у = _у = 0. Из симметрии распределения q' ( у ) относительно прямой O'O следует dq '( у )/ dyI_у = ₀ = 0. Этим условиям удовлетворяет аппроксимирующее соотношение

πψπψ q′(ψ) = q0′cos2+q1′sin2,      (1)

2ψm      ψm в котором коэффициент q ′ найдем из баланса потоков падающего излучения в виде равенства

Q = 2пГ2 (q‘Iо + qIJ , где m     πψ

I = cos²    sinψ d ψ=

₀      2ψ _m

1-cosψ _m -2(ψ _m /π)²

2-2(ψ m /π)²

^{ψ m}     πψ             1-cosψ

I = sin²    sinψ d ψ=2         ^m

^{1    ∫} 0      2ψ m             4-(ψ m /π)²

В итоге получим

q,= q 4 - (У m In)2 .1    ° 2(1 - cos Vm )

, _ УП ⁽² + П) _ ^{1 -} cos V m ^{- 2(} V m ^{1 П}У _k        ¹ + П       ^{2(1 +} П ^{)2(1 - (} V m I ^{П )2} ,

Так как V m = л-у m = n- arctg^n(2 + n) и cos xy_m =-cos Y_m =-1/(1 + r| ) , отношения

q(0) = q'(0)/qo, q = q‘ /qо и q = q/(nr2q0)

и угол у_т можно представить функциями лишь одного аргумента η (рис. 2). На рис. 3 построены рассчитанные с использованием ф о рмулы (1) графики зависимости от отношения У = У / У m относительной плотности q (У) = q (у) / q ₀ падающего на поверхность оболочки собственного излучения поверхности Земли для различных значений параметра η .

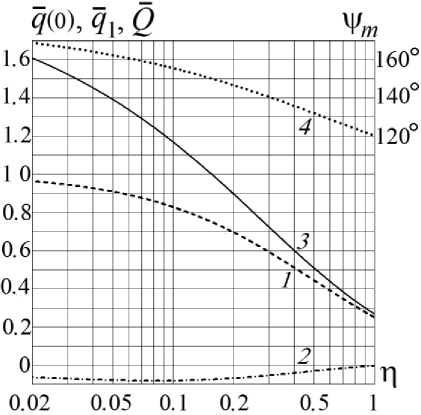
Рис. 2. Графики зависимостей от параметра ƞ :

^{1 —} q ⁽⁰⁾ ; ^{2 —} q 1 ; ^{3 —} Q ; ^{4 — у} т

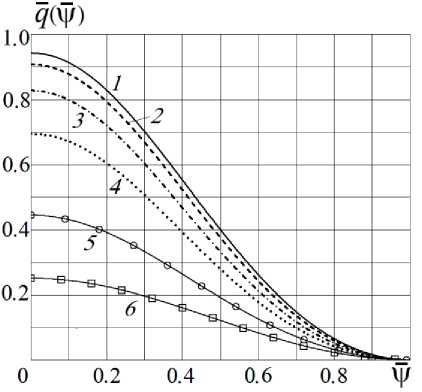
_Рис. 3. Графики зависимостей q (\ |/ ) от отношения У = У / у m при различных значениях параметра q :

1 – 0,03; 2 – 0,05; 3 – 0,1; 4 – 0,2; 5 – 0,5; 6 – 1

Температурное состояние сферической оболочки

Оценки термического сопротивления оболочки из тонкой алюминированной полимерной пленки в направлении нормали к поверхности по- казывают, что температуру оболочки можно принять однородной по ее толщине. Действительно, оболочка из каптона [11], аналогом которого является полиимидная пленка ПМФ-352 с двусторонним покрытием политетрафторэтиленом (тефлоном) [22; 23] с коэффициентом теплопроводности X = 0,17 Вт/(м-К), при толщине h = 30 мкм имеет весьма малое термическое сопротивление h / X ~ 1,8 •Ю-4 м2-К/Вт. Слой напыленного алюминия толщиной h' = 10 нм при коэффициенте теплопроводности X' = 206 Вт/(м-К) [24] обладает термическим сопротивлением h'/X'~ 5-10-11 м2-К/Вт. Даже 150 при завышенной оценке в 200 Вт/м2 возможного значения плотности теплового потока, проходящего через оболочку, получим также завышен- ную оценку перепада температуры по толщине оболочки, не превышающую 0,04 К.

Эффективный коэффициент теплопроводности оболочки в тангенциальных направлениях, оцениваемый по формуле X* = (Xh + X'h) / (h + h ) составит не более 0,18 Вт/(м∙К). Это позволяет при формировании тепловой модели оболочки не учитывать перенос тепловой энергии путем теплопроводности вдоль поверхности оболочки. Малое значение полной теплоемкости оболочки позволяет считать ее температурное состояние установившимся при движении ККА на теневом участке орбиты.

Собственное излучение Земли относится к инфракрасной части спектра и для средней температуры излучающей поверхности Земли, оцениваемой значением 288 К, наибольшая интенсивность этого излучения соответствует, согласно закону Вина [21], длине волны около 10 мкм. При близких к указанному значению температурах допустимо считать коэффициент A' поглощения излучения поверхностью равным ее коэффициенту s' излучения, часто называемому «степенью черноты».

Материал оболочки примем непрозрачным для излучения. Свойства внутренней поверхности оболочки примем соответствующими модели диффузно-серой поверхности [21], что позволяет считать равными коэффициенты A поглощения и ε излучения этой поверхности. Все упомянутые оптические характеристики внешней и внутренней поверхности оболочки полагаем неизменными на каждой из поверхностей. При наличии в оболочке оборудования ККА считаем, что занимаемый им объем достаточно мал. Это дает возможность при анализе переноса излучения внутри оболочки не учитывать возможного взаимного затенения участков ее внутренней поверхности. Отсюда следует, что при осесимметричном относительно прямой O'O (рис. 1) распределении плотности падающего собственного излучения Земли искомое установившееся распределение температуры в оболочке также долж-

Том 2 но быть осесимметричным, описываемым функцией T ( у ) лишь одного аргумента у . Поскольку давление газа в полости оболочки ККА диаметром даже порядка метра не превышает значения в 10 Па [7], а для более крупных оболочек имеет еще меньшее значение, переносом тепловой энергии в этой полости за счет теплопроводности газа (даже в случае использования высокотеплопроводного гелия) можно пренебречь и учитывать теплоперенос лишь путем излучения.

Принятые допущения позволяют перейти к рассмотрению модели непрозрачной для излучения сферической оболочки нулевой толщины радиусом r ₀, равным радиусу средней поверхности реальной оболочки ККА. Двумя близкими сечениями, перпендикулярными прямой O O (рис. 1), выделим из такой условной оболочки кольцевую полосу, положение которой характеризует угол ψ . Ее внешняя поверхность поглощает часть A q '( у ) потока, падающего на оболочку излучения Земли плотностью q' ( у ), и испускает поток собственного излучения плотностью s О 0 T ⁴( у ), где о 0 ~ 5,6693 • 10^-8 Вт/(м2 • К) - постоянная Стефана-Больцмана. Разность плотностей этих потоков составляет плотность q * ( у ) результирующего излучения с внутренней поверхности этой полосы, поступающего в полость оболочки. Тогда уравнение баланса потоков для единичной площадки внешней поверхности кольцевой полосы можно представить в виде

Aq W) —s‘^ 0 ^Т %) = q Чу).      ⁽²⁾

В силу вогнутости внутренней поверхности оболочки на рассматриваемую полосу от соседних кольцевых полос падает поток излучения плотностью q * . Часть Aq * этого потока поглощается, а часть (1 - A ) q^* , отражаясь, снова поступает в полость оболочки (коэффициенты поглощения и отражения для непрозрачной оболочки в сумме составляют единицу). Особенность полости сферической оболочки состоит в том, что для нее q * = const [7-9] т.е. не зависит от угла у . В данном случае при s' = A' имеем

q * = q '= Q / (4n r0)

– среднее по внешней поверхности оболочки значение плотности потока падающего на нее излучения Земли. В итоге уравнение баланса тепловых потоков для единичной площадки внутренней поверхности кольцевой полосы примет вид

Aq '+ q *( v ) = £^ 0 t ⁴( v )           (3)

Исключив из соотношений (2) и (3) величину q^* , при s = A получим формулу

T ⁴(v) = ( Aq ' + Aq ’(v) ) / ( ( A + A ') ^o ) ,  (4)

определяющую установившееся распределение температуры по поверхности оболочки. Из этой формулы, в частности, следует, что температура участка оболочки при ψ ≥ ψ_m , на которую не падает излучение Земли, не зависит от угловых координат. Эту температуру определяют параметр η и значения A и A' .

Оценка отклонения формы оболочки от сферической

Оболочку ККА при неизменной по ее толщине температуре и нагружении только внутренним давлением p допустимо считать безмомент-ной [14], а ее полимерный материал изотропным. Поскольку температурное состояние оболочки осесимметрично относительно прямой O'O (рис. 1), она будет симметричной относительно оси, совпадающей с этой прямой, т. е. безмо-ментной оболочкой вращения относительно этой оси. Для такой оболочки уравнение равновесия в проекции на нормаль к ее средней поверхности (уравнение Лапласа) имеет вид

NV R1 + N2/ R2 = p (5)

где N ₁ и N ₂ – погонные усилия соответственно в меридиональном и окружном направлениях; а R ₁ и R ₂ – радиусы кривизны средней поверхности оболочки в этих направлениях. Для полных деформаций безмоментной оболочки вращения в этих направлениях справедливы соотношения [14]:

e, = (du / d0 + w)/R,e2 (w + u ctg 0) / R2 = ur / r,

где u и w – перемещения точки средней поверхности в меридиональном направлении и в направлении нормали к этой поверхности; θ – угол между осью оболочки и этой нормалью; u r = u • cos 9 + w • sin 9 - перемещение перпендикулярно оси оболочки; r – радиус контура поперечного сечения средней поверхности плоскостью, перпендикулярной оси оболочки.

В предположении упругой работы материала оболочки, согласно обобщенному закону Гука, для полных деформаций в меридиональном и окружном направлениях запишем

e, = (N - vN )/ (Eh + a AT(v)), e2 = (N2 - vN ) / (Eh + a AT(v)), где v, E и α – соответственно коэффициент Пуассона, модуль Юнга и температурный коэффициент линейного расширения материала оболочки; AT(у) = T(у) - T0 - приращение температуры оболочки по сравнению с однородной по ее поверхности температурой T0, при которой оболочка имела сферическую форму с радиусом r0 средней поверхности. При нагружении оболочки вращения только внутренним избыточным давлением p в ее поперечном сечении радиусом r суммарная сила в направлении оси будет равна P = 2πrN1sinθ = πr2p. Отсюда, с учетом равенства r = R2 sinθ и уравнения (5), следует N1 = pr / (2 · sinθ) = pR2 / 2 и N2 = (pR2/2)(2 – R2/R1). Для сферической оболочки в этом случае R1 = R2 и N1 = N2 = pR1/2. Если при осесимметричном распределении температуры по поверхности оболочки ККА в первом приближении принять R1 ≈ R2 ≈ r0, то получим N2 ≈ pR2 / 2 = N1, что, согласно соотношениям (7), приводит к приближенному равенству ε1 ≈ ε2. Тогда из формул (6) следует du/d9 ~ u • ctg9, т. е. u ~ C • sin9, где C = const. В итоге принятого приближения из первых равенств (6) и (7) находим

w * pr2 (1 — v) / (2Eh) + arAT(y) — C cos 0

Перемещение точек средней поверхности оболочки в направлении ее оси равно [14] u 1 = u • sin 9 - w • cos 9 , что с учетом формул для перемещений u и w дает

U « C — (pr0 (1—v) / (2Eh)+aTT(y ))r0cos6

Если за нуль отсчета перемещения u ₁ принять ближайшую к Земле точку при ψ = θ = 0 (рис. 1), то получим

C = P ( Г ) + ^ o)²(1 - v )/ (2 Eh )+ «0 r o + W o)A T ( ^ )

и

U1 *( p (r0 + wo)(! -v)/(2Eh ) + aA T (v) )• (8)•( r0 + w0)(1 - cos 6)

Из вторых равенств (6) и (7) следует

ur * (РГ (1—v) / (2Eh) + a^T(y)) r0 sin 0 (9)

Из формул (8) и (9) видно, что изменение давления в рамках принятого приближения не искажает форму сферической оболочки, а лишь приводит к одинаковому во всех точках средней поверхности некоторому приращению ее первоначального радиуса r ₀. Отклонение формы оболочки от сферической непосредственно связано с неравномерностью распределения температуры по ее поверхности, причем эта неравномерность возникает, согласно формуле (4), только на облучаемой Землей части этой поверхности. Из соотношений (8) и (9) следует, что перемещения, вызванные лишь неравномерностью распределения температуры, при отождествлении в первом приближении угла θ с углом ψ можно оценить по формулам

u* = aAT(y) r0 sin ^, ux* = aAT(y) r0 (1 - cos y)

Том 2

Результаты расчетов

Степень влияния излучения Земли на температурное состояние оболочки ККА зависит от значения параметра η . Для сравнения проведем вычисления при четырех значениях этого параметра, равных 0,03; 0,05; 0,1 и 0,2, что соответствует значениям высоты H над ее поверхностью Земли, равным 191,3; 318,6; 637,1 и 1274,3 км.

Пусть оболочка ККА изготовлена из упомянутой выше полиимидной пленки ПМФ-352 с напылением алюминием на внешней поверхно-152 сти. Коэффициент поглощения A внутренней поверхности такой оболочки будет не менее 0,5 [25]. Увеличение значения A приводит к выравнива- нию распределения температуры по поверхности оболочки и уменьшению наибольшего значения T(0) температуры при ψ = 0 в точке, ближайшей к поверхности Земли. Для сравнения при проведении расчетов примем два крайних значения A = 0,5 и A = 1 (второе значение для полости оболочки соответствует модели абсолютно черного тела [21]).

Для коэффициента поглощения слоя напыленного алюминия в его исходном состоянии после напыления можно использовать линейную зависимость A' ( T) = 0,025 - 0,00007 • (300 - T) от температуры T [26], установленную в промежутке от 100 К до 300 К для охлажденного расплава алюминия с неокисленной поверхностью. Однако при контакте слоя алюминиевого покрытия с атмосферным воздухом происходит окисление поверхности этого слоя и увеличение этого коэффициента. Кроме того, в процессе пребывания в космосе поверхность оболочки подвержена микрометеоритному воздействию, что приводит к возникновению шероховатости поверхности покрытия и возрастанию его коэффициента излучения. В силу отсутствия определенности величины коэффициента A' расчеты проведены для трех его дискретных значений, равных 0,015; 0,05 и 0,15.

Результаты расчетов распределения температуры по поверхности сфериче с кой оболочки ККА в зависимости от отношения V = V / V m Для указанных значений параметра η приведены на рис. 4–7. На всех этих рисунках сплошные кривые построены при значении A = 0,5, а штрих-пунктирные – при значении A = 1. Кривые 1, 2 и 3 отвечают значениям соответственно 0,015; 0,05 и 0,15.

При фиксированном сочетании коэффициентов поглощения A и A' наибольшая температура сферической оболочки, соответствующая значению ф = 0, и температура изотермического участка, отвечающая значению ф = 1, убывают по мере возрастания параметра η. Это вызвано увеличением высоты ККА над поверхностью Земли и связано с уменьшением потока излучения, падающего на поверхность оболочки. Но даже при η = 0,2 общий уровень температур (рис. 7) остается допустимым для такого полимерного материала, как пленка ПМФ-352 [27; 28]. Из представленных результатов видно, что при фиксированных значениях параметра η и коэффициента A неравномерность распределения температуры увеличивается с увеличением коэффициента A', а при неизменных значениях η и A' переход от A = 0,5 к A = 1, как и следовало ожидать, в связи с выравниванием распределения температуры по поверхности оболочки температура изотермического участка оболочки возрастает.

Найденные распределения температуры по поверхности оболочки ККА могут быть использованы для оценки по формулам (10) отклонения формы этой оболочки от исходной сферической.

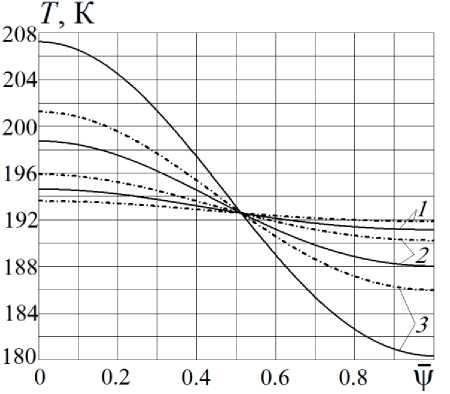
Рис. 4. Графики зависимости T ( v ) от V при значении параметра η = 0,03

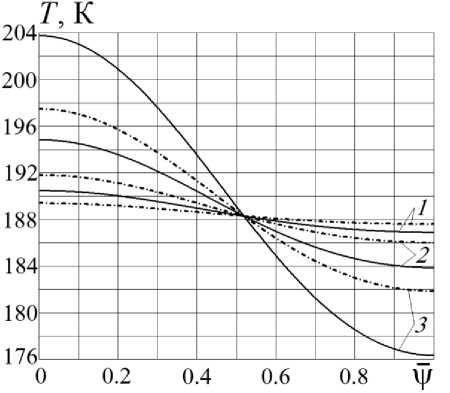
Рис. 5. Графики зависимости T ( v ) от V при значении параметра η = 0,05

На рис. 8 и рис. 9 штрихпунктирной дугой полуокружности представлен контур продольного сечения средней поверхности оболочки при однородном распределении температуры T ₀, равной рассчитанному значению T ( п /2) (отсчет угла ψ происходит от положительного направления оси Ox ₁).

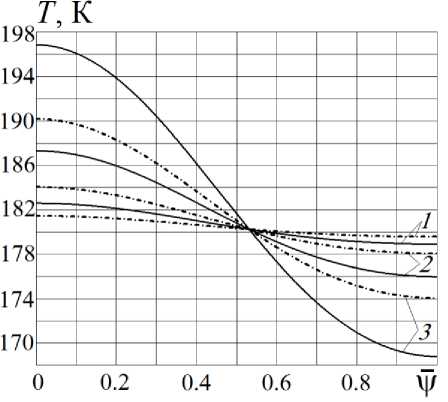
Рис. 6. Графики зависимости T ( у ) от \|/ при значении параметра η = 0,1

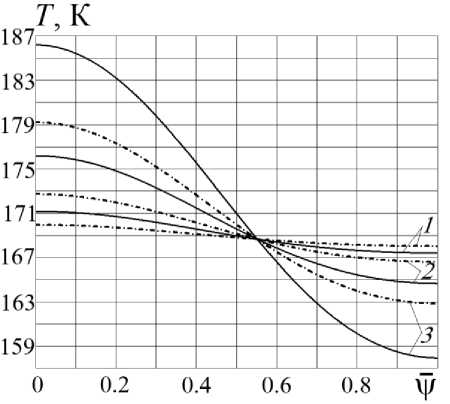
Рис. 7. Графики зависимости T ( у ) от )|/ при значении параметра η = 0,2

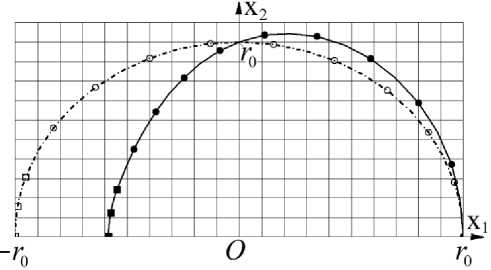
Светлыми кружками на этой полуокружности отмечена часть контура, на которую падает излучение Земли, а светлыми квадратами – его часть с постоянной температурой. Смещение темных кружков и квадратов на сплошной кривой по отношению к светлым позволяет сравнить степень локального искажения исходного контура средней поверхности при рассчитанном неоднородном распределении температуры T ( у ). На участке контура с темными квадратами температура постоянна. Поэтому эта часть оболочки сохраняет сферическую форму, но с меньшим по сравнению с r 0 радиусом r * , определяемым отношением ( r₀ - r ) / r ₀ = a (T П 1 2) - T( п )). Для наглядности относительное изменение этого радиуса и смещение темных кружков по отношению к светлым увеличено на рис. 8 в 0,02 • К^-1/а раз, а на рис. 9 - в 0,05 • К^-1/а раз.

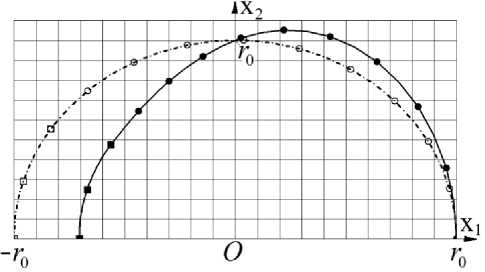
Рис. 9. Отклонение формы контура средней поверхности оболочки при η = 0,2

Из сравнения штрихпунктирной полуокружности со сплошной кривой видно, что в окрестности наиболее близкой к Земле точки оболочки ее радиусы кривизны увеличиваются по сравнению с исходным значением, равным r ₀. Затем по мере возрастания угла ψ при продолжающемся росте значения R ₂ радиус кривизны R ₁ начинает убывать. При ψ >  π /2 после достижения радиусом R ₂ максимальной величины его значение начинает убывать и сближается с возрастающим значением R ₁ до их совпадения при у ~ 2,83 ~ 162° на рис. 8 и при у ~ 2,56 ~ 146° на рис. 9.

Заключение

Тепловая часть представленной комплексной математической модели, описывающая установившееся температурное состояние алюминированной полимерной сферической оболочки ККА, находящегося на затененном участке околоземной орбиты, позволяет установить зависимость распределения температуры по поверхности этой оболочки от высоты космического

^{Рис. 8. Отклонение формы контура средней} аппарата над поверхностью Земли и от коэффи-^{поверхности оболочки при η = 0,05} циентов излучения внешней и внутренней по-

Том 2

верхностей оболочки. Эта зависимость исполь- зультаты могут быть полезны для прогноза рабо-зована для оценки отклонения формы оболочки тоспособности ККА на затененном участке око-от сферической, вызванного неравномерностью лоземной орбиты.

распределения температуры. Полученные ре