Температуропроводность и электросопротивление стали 38ХН3МА вблизи фазовых превращений

Для улучшения механических свойств и эксплуатационных характеристик горного инструмента учеными ведутся исследовательские работы не только по созданию новых высокопрочных конструкционных материалов, но и по формированию высокопрочного состояния в уже известных сталях и сплавах. В последнем случае основные усилия направлены на использовании различных видов фазовых превращений, возникающих в сплавах при изменении температуры. Так, например, существование в железе и его сплавах прямого α → γ и обратного γ → α мартенситного превращения, который, как правило, сопровождается большим температурным гистерезисом, открывает возможность с помощью локального нагрева (лазерного или индукционного) изменять заданным образом фазовый состав по объему изделия, т.е. получить материал с неоднородными физическими свойствами [1, 2]. Однако для практического применения такого метода необходимо достаточно точно идентифицировать температуры начала и конца фазовых превращений в конкретном сплаве, а также величину температурного гистерезиса с учетом скорости его нагрева и охлаждения.

Как известно, важную информацию о температуре и виде фазового превращения в металлах и сплавах могут дать исследования температурных зависимостей удельного электросопротивления ρ и коэффициента температуропроводности a [3, 4]. Такой подход обусловлен тем, что зависимости ρ ( Т ) и a ( Т ) в окрестности температур фазового перехода ведут себя строго определенным образом. При фазовом переходе первого рода (полиморфные превращения) удельное электросопротивление и температуропроводность изменяются скачком. Вблизи температур фазового превращения второго рода (точка Кюри, порядок-беспорядок) зависимость ρ ( Т ) имеет аномалию в виде точки излома или точки перегиба, а зависимость a ( Т ) имеет ярко выраженную форму λ -образного минимума [5, 6].

Кроме того, эффективное применение конструкционных материалов невозможно без знания их температурных зависимостей теплофизических и кинетических свойств в широком интервале температур (вплоть до плавления). Недостаток такой экспериментальной информации является основным препятствием на пути выяснения особенностей физических процессов, протекающих в этих сплавах. Такие данные необходимы также для математического моделирования процесса распространения тепла в них, которое требуется при проведении разнообразных проектно-конструкторских работ и при разработке технологических приемов по упрочнению сплавов.

Целью настоящей работы является измерение температуропроводности, удельного электросопротивления и оценка коэффициента теплопроводности хромоникельмолибденовой среднелегированной стали марки 38ХН3МА, а также определение температур начала и конца фазовых превращений в процессе нагрева и охлаждения в интервале температур от 300 до 1600 K. Интерес к данным исследованиям обусловлен тем, что сталь марки 38ХН3МА широко применяется для изготовления ответственных деталей с высокими требованиями по механическим свойствам при нормальных и повышенных температурах.

Обзор научной и справочной литературы показал, что экспериментального исследования температурной зависимости коэффициента температуропроводности a ( Т) этой марки стали не проводилось, а сведения о температурных зависимостях удельного электросопротивления р ( Т) и коэффициента теплопроводности Х ( Т ) имеются только до температуры 1073 K (800 ° С) [7, 8].

Методика измерений

Образцы для исследования температуропроводности и удельного электросопротивления вырезались из одного и того же прутка стали марки 38ХН3МА электроискровым методом с постоянным охлаждением в масле. Готовые образцы перед загрузкой в измерительную ячейку подвергали дополнительной ручной шлифовки. Измерения размеров, полученных образцов, выполняли на приборе ИЗВ-1 с точностью ±1 мкм. Химический состав стали 38ХН3МА приведен в [7].

Измерения температурных зависимостей температуропроводности a ( T) выполняли методом плоских температурных волн [9] на двух оригинальных автоматизированных установках, с общей относительной среднеквадратичной погрешностью, не превышающей 3 % при доверительной вероятности 0.95.

На первой установке измерения температуропроводности проводили в атмосфере чистого гелия, который запускали в водоохлаждаемую камеру после предварительного вакуумирования до давления 10^-2 Па. Среднюю температуру образца изменяли при помощи кольцевой печи электросопротивления по заданному временному графику, а температурные волны возбуждали модулированным по амплитуде излучением лазера ЛГН-701 [10]. Образец для проведения исследований на этой установке имел форму плоскопараллельной квадратной пластины размером 12x12 мм² и толщиной 1.489 мм. Оптимальную частоту модуляции лазерного излучения для данного образца выбирали из интервала 6 <  v < 12 Гц. Средняя скорость нагрева и охлаждения образца на этой установке не превышала 10 K/мин.

На второй установке нагрев образца и генерацию колебаний температуры на его поверхности осуществляли в вакууме частично модулированным пучком электронов, ускоряемых высоковольтным электрическим полем, приложенным между катодом и образцом [11]. Образцы представляли собой плоскопараллельные диски диаметром 10 мм и толщиной 0.503 и 0.66 мм. Модуляцию электронного пучка осуществляли с частотой, лежащей в интервале от 8 до 32 Гц. Максимальная скорость нагрева исследуемых образцов за пределами температур фазовых переходов на этой установке достигала значений ~200 K/мин.

Колебания температуры на поверхности образцов (противоположной к нагреваемой) на обеих установках регистрировали фотодатчиками на основе германиевого фотодиода. Среднюю температуру образцов измеряли термопарой ВР5/ВР20 толщиной 50 мкм, концы которой приваривали точечной сваркой к поверхности в центре образца без образования спая. Сигналы с датчиков после прохождения через линейные нормирующие цепи подавались на внешний анало- го-цифровой преобразователь Е14-440 и затем поступали в компьютер для дальнейшей обработки. Определение амплитуды и фазового сдвига колебаний температуры на второй поверхности образца по отношению к колебаниям теплового потока осуществляли в соответствии с процедурой, использующей преобразование Фурье.

Измерения удельного электросопротивления выполняли четырехзондовым потенциометрическим стационарным методом в атмосфере гелия [5, 12]. Исследуемые образцы представляли собой параллелепипеды высотой 12 мм и сечением 1.5×1.5 мм2. К ним на расстоянии 8-10 мм друг от друга на одной и той же плоскости образца приваривались две платина-платинородиевые термопары толщиной 50 мкм, одноименные ветви которых использовались затем в качестве потенциальных электродов для измерения напряжений при заданном токе в образце. Максимальная (при доверительной вероятности 0.95) относительная погрешность, обусловленная в основном погрешностью определения геометрических размеров рабочего участка, не превышала 2 %. Скорость нагрева и охлаждения образца на этой установке при переходе из одного стационарного состояния в другое не превышала 10 K/мин.

Экспериментальные результаты и обсуждение

Результаты экспериментального исследования температурных зависимостей коэффициента температуропроводности стали марки 38ХН3МА частично представлены на рис. 1. Эти данные получены нами в серии измерений при нагреве (кривая 1 ) и охлаждении (кривая 2 ) исходного (не отожженного) образца в интервале температур 600–1400 K, а затем при нагреве того же образца (кривая 3 ) до температуры 1600 K.

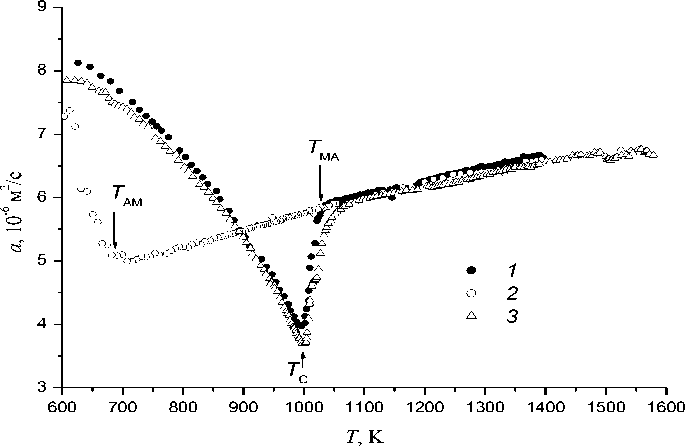
Рис. 1. Температурная зависимость температуропроводности стали марки 38ХН3МА: 1 — первый нагрев, 2 — охлаждение, 3 — повторный нагрев

Из хода графических зависимостей a ( Т ) видно, что при нагреве образца вблизи T С = 1000±5 K наблюдается четко выраженный λ -минимум температуропроводности, соответствующий фазовому переходу второго рода. Значение T С совпадает с температурной Кюри бинарного сплава Fe-Ni с содержанием никеля 3 ат. % [12]. Поскольку в исследуемой нами стали 38ХН3МА основным легирующим элементом являются Ni (~3%), то можно считать, что при 1000 K сталь претерпевает магнитное фазовое превращение (температура Кюри), при котором ферромагнитный мартенсит (α-железо) переходит в парамагнитное состояние (β-железо).

При дальнейшем повышении температуры в интервале от 1030 до 1060 K на кривой 3 виден резкий скачок температуропроводности от 4.5 ⋅ 10^-6 до 5.8 ⋅ 10^-6 м²/с, который по форме соответствует размытому фазовому переходу первого рода. Поэтому можно предположить, что в этом интервале температур парамагнитный мартенсит постепенно переходит в аустенит ( γ -железо). Поскольку выше этого интервала температур зависимости a ( Т ), полученные при нагреве и затем при охлаждении от 1600 K, совпадают, то можно утверждать, что полное превращение мартенсита в аустенит происходит при Т МА = 1060 K. Полученные значения температур фазовых превращений хорошо согласуются с температурами критических точек A C 1 (993 K) и A C 3 (1063 K), представленными для стали марки 38ХН3МА в [7].

При понижении температуры равновесная парамагнитная аустенитная фаза переохлаждается до T AM = 670 ± 5 К и затем начинает переходить в ферромагнитный мартенсит, что характеризуется изломом на кривой a ( T ). Подобный температурный гистерезис температуропроводности наблюдается для других типов сталей на основе железа, например 16Х12В2ФТаР и ЧС-139 [13, 14].

При повторном нагреве образца значения температуропроводности во всем исследованном диапазоне температур лежат ниже значений, полученных при первом нагреве образца. Можно предположить, что эта разница, сравнимая с погрешностью измерения температуропроводности, связана с исходным состоянием не отожженного образца.

Анализ кривых удельного электросопротивления по выявлению температур фазовых переходов выполним с учетом следующих соображений. В случае отсутствия каких-либо превращений в исследуемом сплаве 38ХН3МА температурный ход зависимости ρ ( Т ) образца должен иметь линейный вид. Возникновение любых отклонений от линейности в процессе нагрева или охлаждения следует рассматривать как развитие в образце фазовых или внутри фазовых превращений.

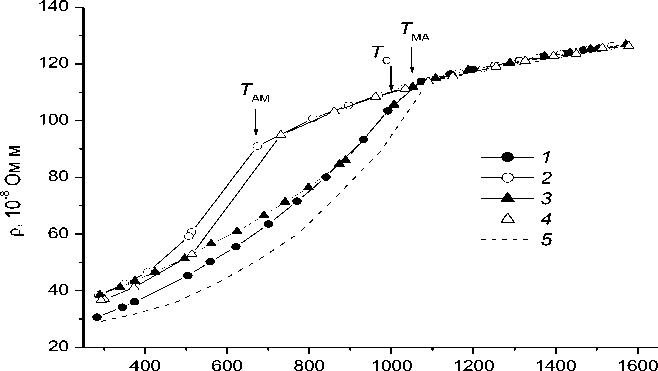
Экспериментальные данные по удельному электросопротивлению в виде температурных зависимостей представлены на рис. 2. Здесь показаны зависимости ρ ( Т ) (кривые 1 и 2 ), полученные нами в цикле «нагрев-охлаждение» исходного образца, и кривые 3 и 4 , полученные при повторных циклированиях того же образца до температуры ~1600 K.

Измерения показывают, что при нагреве стали 38ХН3МА от 300 до 1060 K наблюдается явный нелинейный рост электросопротивления (кривые 1 и 3) с изменением кривизны нелинейности (с положительной на отрицательную) вблизи 1000 K. Такая зависимость ρ(Т) в сплавах на основе железа связана с магнитным разупорядочением, происходящем в α-железе. Значит, вблизи 1000 K мартенсит переходит из феромагнитного состояния в парамагнитное состояние. Линейный рост электросопротивления выше TМА = 1060 K свидетельствует о завершении перехода парамагнитного мартенсита в парамагнитный аустенит в интервале 1000–1060 K.

Охлаждение образцов от 1600 K показывает, что обратное превращение аустенита в мартенсит начинается при более низкой температуре. На это указывает резкое отклонение от линейности зависимости ρ ( Т ) (кривые 2 и 4 ) вблизи T AM = 670 K. Однако точно определить температуру окончания данного превращения невозможно из-за плохой воспроизводимости результатов измерения электросопротивления при T = 300 K.

Следует также заметить, что форма экспериментальных кривых, полученных при нагреве, в интервале температур от 300 до 1060 K хорошо согласуется с ходом зависимости ρ(Т), построенной по справочным данным для этой марки стали (кривая 5) [7]. В то же время видно, что разница в численных значениях удельного электросопротивления при фиксированной температуре существенна и превышает погрешность измерений. Действительно, при Т = 873 K измеренное нами значение ρ(Т) = 84.6×10-8 Ом⋅м больше справочного значения на 10.4×10-8 Ом⋅м. Отклонение составляет 12 %. Если при этом учесть, что кривая ρ(Т) при первом нагреве исходного образца (кривая 1) до 900 K лежит ниже кривой 3, полученной при его повторном нагреве, то можно предположить, что данные расхождения могут быть связаны, во-первых, со скоростью нагрева и охлаждения стали (кривая 1), а, во-вторых, с наличием остаточного аустенита после охлаждения образца от высокой температуры (кривая 3).

T , K

Рис. 2. Температурные зависимости электросопротивления стали марки 38ХН3МА при термоциклировании: 1 — первый нагрев; 2 — охлаждение; 3,4 — повторный нагрев и охлаждение; 5 — справочные данные [7].

В связи со сложной зависимостью коэффициента температуропроводности и удельного электросопротивления от температуры получить единую аппроксимацию экспериментальных данных не представляется возможным. Поэтому ис- 52

пользовалась обработка в ограниченных температурных диапазонах. В интервале 600–1000 K получены следующие зависимости:

a ( T ) = (9.484 - 5.523 ⋅ 10 ^{- 3} T + 1.283 ⋅ 10 ^{- 5} T ² - 1.312 ⋅ 10 ^{- 8} T ³ ) ⋅ 10 ^{- 6} м²/с, ρ ( T ) = (10.28 + 0.13 T - 1.508 ⋅ 10 ^{- 4} T ² + 1.138 ⋅ 10 ^{- 7} T ³ ) ⋅ 10 ^{- 8} Ом м.

При охлаждении от 1600 K до температуры Т АМ аппроксимационные уравнения имеют вид:

a ( T ) = (2.514 + 4.08 ⋅ 10 ^{- 3} T - 8.59 ⋅ 10 ^{- 7} T ² ) ⋅ 10 ^{- 6} м²/с, ρ ( T ) = (8.992 + 0.18 T - 9.967 ⋅ 10 ^{- 5} T ² + 2.076 ⋅ 10 ^{- 8} T ³ ) ⋅ 10 ^{- 8} Ом м.

Достоверность аппроксимации составила R2 = 0,9996. Эти зависимости описывают данные, полученные на отожженных образцах при скоростях нагрева не превышающих 10 K/мин.

Для определения коэффициента теплопроводности использовали соотношение [16]:

λ = ac_p d ,                                    (1)

где а — температуропроводность; с p — удельная теплоемкость при постоянном давлении; d — плотность образца.

С помощью соотношения (1) по результатам измерения температуропроводности была рассчитана температурная зависимость коэффициента теплопроводности λ ( Т ). В расчетах зависимости λ ( Т ) использовали результаты измерения температуропроводности a ( T ), а также литературные данные по температурным зависимостям удельной теплоемкости с р ( Т ) и плотности d ( Т ) для чистого железа [4] с учетом смещения температуры Кюри и температуры полиморфного β → γ превращения, характерных для стали 38ХН3МА. Такое заимствование вполне оправдано, поскольку в данном сплаве содержание железа составляет 94 вес. %, а основными легирующими элементами являются Ni (~3 вес. %) и Cr (~1 вес. %).

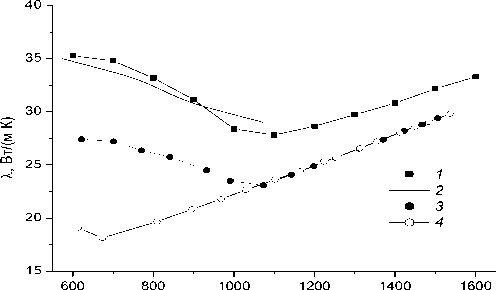
T , K

Рис. 3. Температурные зависимости коэффициента теплопроводности стали марки 38ХН3МА: 1 — коэффициент полной теплопроводности; 2 — справочные данные [8];

3, 4 — электронная составляющая коэффициента теплопроводности при нагреве и охлаждении соответственно

Результаты расчета температурной зависимости коэффициента теплопроводности представлены на рис. 3 (кривая 1 ). Общая погрешность определения X ( Т) , исключая окрестности температур фазовых переходов, оценивается нами в 5-7 %. Полученные значения в интервале температур от 600 до 1073 K хорошо согласуются с экспериментальными данными (кривая 2 ), представленными в марочнике [8]. Расхождение наших результатов и литературных данных не превышает 4 %.

В металлах и сплавах, испытывающих разного рода фазовые превращения, теплопроводность можно оценить также исходя из того, что перенос тепловой энергии в них осуществляется двумя типами носителей: электронами проводимости и колебаниями кристаллической решетки [4], т.е.

x = x э + X ф , где X э — электронная составляющая, X ф — решеточная составляющая теплопроводности.

Температурную зависимость электронной составляющей теплопроводности можно определить с помощью закона Видемана-Франца X = LT / р по результатам измерения электросопротивления р ( Т ) в цикле «нагрев-охлаждение». Такая оценка X э ( Т) с использованием стандартного числа Лоренца представлена на рис. 3 (кривые 3 и 4 ).

Из рисунка видно, что с повышением температуры полная теплопроводность Х ( Т мартенсита нелинейно (с отрицательной кривизной) убывает, а полная теплопроводность Х ( Т аустенита линейно возрастает. Аналогичным образом ведет себя при нагреве образца и электронная составляющая X э (кривая 3 ). Из сравнения графиков можно заключить, что рост полной теплопроводности аустенита (выше 1100 К) обусловлен вкладом электронной составляющей X э , которая при высоких температурах дает основной вклад в полную теплопроводность. Вклад решеточной составляющей X ф здесь не превышает 10 %. Вклад X ф в теплопроводность мартенсита более существенен и составляет 18-20 %.

Заключение

Получены новые экспериментальные данные по коэффициенту температуропроводности а и удельному сопротивлению р ферритно-мартенситной стали 38ХН3МА при циклировании в режиме «нагрев-охлаждение» от 300 до 1600 K. По этим данным определены температуры начала и конца структурного фазового перехода мартенсит-аустенит и температура магнитного (ферромагнетик-парамагнетик) превращения в мартенсите при скоростях нагрева образцов, не превышающих 10 K/мин.

Показано, что магнитное превращение в сплаве проявляется в виде глубокого минимума на температурной зависимости a (T), а взаимные фазовые переходы аустенит-мартенсит происходят со значительным температурным гистерезисом. Показано также, что для определения температур начала и конца фазовых превращений аустенит-мартенсит, а также величины температурного гистерезиса в стали 38ХН3МА лучше всего подходит анализ температурной зависимости температуропроводности а ( Т).

Полученные данные могут быть использованы при тепловых расчётах узлов и деталей, изготовленных из стали 38ХН3МА и работающих при высоких темпе- ратурах. На основании полученных результатов осуществима возможность с помощью локального нагрева (лазерного или индукционного) изменять заданным образом фазовый состав по объему готового изделия, т.е. получить материал с требуемыми физическими свойствами.