Тензорная методология для поиска оптимальной структуры системы

Задачи поиска оптимальной структуры сети

Поиск  решений оптимальных в том или ином смысле составляет важный класс исследовательских инженерных задач. Здесь можно сослаться на многочисленные постановки задач такого рода в различных предметных областях, вместе с тем демонстрирующих единство в описании, методах решения [1, 2, 3, 4, 5, 6].  Для нас более важным является рассмотрение вопросов связанных с поиском оптимальной структуры системы, а также получение ответа на следующие вопросы:

• 1.    Можно ли решать данный класс задач тензорными методами;

• 2.    Существует ли особенности в описании, построении, преобразовании тензорных моделей для задач данного класса;

• 3.    Что дополнительно дают тензорное описание и тензорные методы решения.

В данной работе ограничимся рассмотрением часто встречающихся моделей прикладных задач линейного программирования, которые имеют сетевую структуру. Сетевая структура обладает особенностью: во всех ограничениях коэффициенты при управляемых переменных могут принимать одно из двух ненулевых значений, а именно +1 или -1 в соответствии с установленным правилом выбора знака. При наличии такой структуры задачу можно свести к оптимизации потоков некоторой однородной продукции на определенной сети. Определение оптимальных потоков на сети требует построения не только оптимальных планов, за каждым планом перевозок закрепляется определенная структура сети, которая итерационно трансформируется к оптимальной. Исследование данного класса задач тензорными методами анализа сетей впервые было дано в книге Г.Крона «Исследование сложных систем по частям - диакоптика» [1]. Изучение предложенных в ней электрических моделей транспортных задач оставило много вопросов, которые и послужили стимулом для предлагаемой работы.

Нами предполагается пройти путь от описания, построения и преобразования структуры сетевых моделей относительно простых транспортных систем, к задачам описания, построения и преобразования структуры моделей более сложных экономических, технических систем, которые будут рассмотрены в другой работе.

Базовые понятия и соотношения для сетевых моделей транспортной задачи

Введем сетевые понятия для транспортной задачи. Начнем с понятия сети. Под сетью будем понимать информационную модель задачи, имеющей вид ориентированного или не ориентированного графа, вершины и дуги (ветви), которого соответствуют элементам предметной области.

Чаще всего вершины (узлы) соответствуют отправителям или получателям некоторой продукции соответствующей некоторой предметной области, а дуги различным путям или каналам доставки.

Количество ветвей в транспортной задаче равно числу путей. Обозначим переменные, связанные с каждой ветвью как .'’ 729; = ■ 1 ^ j они будут обозначать потоки вещества, энергии, информации (ВЭИ), которые передаются по данной ветви.

Количество узлов в сетевой схеме транспортной задачи равно общему числу пунктов отправления и пунктов назначения. Обозначим переменные связанные с каждым узлом через у. 7~9 ; = ■ 1 "; j; они будут обозначать потенциальные затраты, которые несет поставщик или потребитель на единицу передаваемого или потребляемого в данном узле количества вещества, энергии, информации, образуя при этом доход владельцев транспортной системы. Обозначим через: 7 j = ■ 1 к j; - затраты, связанные с транспортировкой груза по каждому j-му пути; .".^:. - значения отгружаемых и потребляемых ресурсов в каждом :- ом узле; :у - матрица коэффициентов, принимающая значения коэффициентов {1,-1,0} в зависимости от того, входит j-ая ветвь в i-ый узел или выходит из него или вообще не связана с данным узлом.

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление»

www.rypravlenie. ru

том 8 № 2 (15), 2012, ст. 5

Теперь можно сделать формальную постановку прямой и двойственной транспортной задачи определения оптимального распределения потоков по транспортным каналам или потенциалов в узлах следующим образом [2]:

Прямая задача.                         Двойственная задача

f(x)=                          (A)             g(y)=                    (B)

(C)                                        (D)

;                                        любое число.

Для прямой задачи при заданных           – найти такие значения потоков для отправителей и получателей ресурсов, которые обеспечат функции f(x) затрат минимальное значение при заданных ограничениях.

Для двойственной задачи при заданных           – найти такие значения доходов владельцев транспортной системы , которые обеспечат функции g(y) максимальное значение при заданных ограничениях.

Для любых допустимых планов x=(        ) и   y=(         ) прямой и двойственной задач справедливо неравенство:

у™ h v. < Уп ст                                     m

Существуют две очень важные теоремы двойственности, которыми пользуются при решении задач линейного программирования. Для транспортной сети они могут быть сформулированы так:

• •    первая теорема двойственности.

Если одна из пары двойственных задач разрешима, то разрешима и другая задача, причем оптимальное значение целевой функции прямой и двойственной задач совпадают

у™ = У" сх*

где:         оптимальные планы двойственных задач.

• •    вторая теорема двойственности.

Чтобы допустимые решения { } и { } пары двойственных задач были оптимальными необходимо и достаточно, чтобы выполнялись условия

v*/y«  а-Х*-ЬЛ = 0(3)

0(3)

у« т-Чс — Уm d -v4 = 0

= 0(4)

Из этих двух соотношений следуют следующие условия оптимальности для пары двойственных задач:

• 1)    Если2”=!^/^ < ^i то ^ = 0,

• 2)    Если^>° , то S/=i^aij"^xj — ^i ,

• 3)    Если У™ n.w* то r* = 0

• 3)    Если                   , то Xj — и ,

• 4)    Если г* > 0 то У™ _ Если         , то

Можно отметить, что в сетевой формулировке транспортная задача становится геометрически наглядной, чем в алгебраической постановке, более удобной для формирования образов, обеспечивающих геометрический фон поиска оптимального решения. Однако сама сеть, представляется, по сути, графом, имеет существенно упрощенные модели элементов, связей, структуры, которые, для различных предметных областей, могут иметь более сложные линейные и не линейные формы. Структура сети здесь не становится самостоятельным объектом исследований, а используется для задания ограничений и интерпретации промежуточных и конечных результатов. Далее мы будем говорить о сети, состоящей из элементов потокового и потенциального типа, на которых оказывают действие внутренние и внешние факторы (внешние и внутренние источники потоков, потенциалов), а сами элементы могут обладать дополнительными свойствами. Сеть такого рода представляет собой уже гораздо более богатую с содержательной точки зрения модель процессов некоторой предметной области.

Тензорно-геометрическая интерпретация описания, построения и решения сетевой транспортной задачи

Сеть как физическая структура

• 1.    Будем рассматривать сеть как физическую структуру, то есть ориентированный граф, вместе с наложенными на него потоковыми или потенциальными процессами. В этом смысле транспортная сеть, связанная с транспортировкой чего либо, представляется структурой, на которую наложены физически измеримые потоковые (контравариантные) и потенциальные (ковариантные) переменные.   «Природа» контравариантности и

• ковариантности переменных связана с законами их преобразования и существованием инварианта мощности [1, 5]. Говоря о «транспортных» задачах мы будем иметь в виду транспортировку ресурсов в виде вещества, энергии, информации, коротко ВЭИ, которые могут быть переданы по транспортным каналам (путям) от поставщика к потребителю. Причем, потоковые переменные, всегда будут связаны с ветвями сети, а потенциальные

• 2.    Потоковые и потенциальные переменные, посредством которых мы параметризуем замкнутые и разомкнутые пути, полностью характеризуют сеть. Задаваемые связи между

• 3.    Сеть может быть выделена из другой сети и эта другая сеть может оказывать влияние на поведение рассматриваемой сети. Можно сказать иначе:  на сеть могут быть

• 4.    Каждый элемент в транспортной сети, в общем случае, может входить как в некоторый замкнутый путь, так и одновременно в некоторый разомкнутый путь. Поэтому, по такому элементу могут протекать одновременно разные потоки: во-первых, те, которые образуются внутри замкнутых контуров, и, во-вторых, те, которые вызваны внешними потоковыми воздействиями и протекают по открытым путям. При преобразовании системы координат сети происходит перераспределение внутренних потоков и внешних потоков в каждом элементе. Каждый элемент сети может иметь  связь с  источником потенциала

переменные с двумя узлами ветви. n - независимых потоковых переменных будут характеризовать аналогичное количество независимых путей, по которым транспортируются ВЭИ. Будем различать два вида путей: разомкнутый путь и замкнутый путь. Каждый путь характеризуется своей границей, в качестве которой будем рассматривать узлы, ограничивающие тот или иной путь, имеющий свое начало и конец. У замкнутого пути – начало пути и конец пути совпадают. Понятно, что число узлов, введенное таким образом у замкнутого пути, будет -n, а разомкнутого пути будет равно -2n. Если с каждым узлом разомкнутого пути связать некоторый потенциал, то разности потенциалов можно придать определенные знак и смысл потенциальной переменой, которая также будет характеризовать тот или иной путь, но несколько в другом смысле. Число потенциальных переменных (когда все разомкнутые пути независимы) будет совпадать с - n.

Когда из разомкнутых путей построена сеть, в которой ветви, связанные посредством своих границ, образуют число узлов, совпадающее с числом ветвей, т.е. m = n, то такая связанная сеть будет относиться к чисто узловой. Если число узлов m< n, то сеть обязательно будет иметь замкнутые пути (контуры), число которых будет: n-(m-1)=N и независимые разомкнутые пути - число которых M=m-1. Построение сетевой структуры определенного типа приводит к тому, что потоковые и потенциальные переменные, накладываемые на каждый элемент пути со своими границами, перестают быть независимыми. Для данных переменных построенная сетевая структура формирует определенные связи (ограничения). Если таких независимых ограничений M, то каждое из множеств потоковых и потенциальных переменных может быть разделено на два непересекающихся подмножества. Если обозначить множество потоковых переменных через     , где j= 1,...,n; и связать их с замкнутыми путями, а множество потенциальных переменных через     где i= 1,...,n; и связать их с разомкнутыми путями, то множество обозначенных переменных разбиваются на следующие подмножества {:<"'• :< '},{ ";. , w.}, где: Л= ■ 1 Л j; х= N — 1 Л — М ■; N=n-M – число степеней свободы (число независимых потоковых переменных) для потоковой переменной и число независимых ограничений для потенциальной переменной, M – число независимых ограничений для потоковой переменной и число степеней свободы для потенциальной переменной. Эти множества и подмножества потоковых и потенциальных переменных при построении геометрической теории сети образуют соответствующие пространства и подпространства.

потоковыми и потенциальными переменными позволяют построить геометрические объекты прямого       и обратного преобразования , осуществляющие взаимосвязь между представлениями потоковых и потенциальных переменных в разных системах координат, а также полностью характеризуют структуру и многочисленные свойства самой сети. Между потоковыми и потенциальными переменными, заданными на сети существуют глубокие связи, которые порождают двойственный характер их поведения и преобразования. Любая связанная сеть, за исключением не связанной - примитивной сети, т.е. сети состоящей из не связанных между собой элементов, накладывает на потоковые и/или потенциальные переменные определенные ограничения – связи. Если какой либо контравариантный потоковый вектор, заданный в новой системе координат, обращается в ноль – т.е. задано ограничение, то это означает, что замкнутый путь разорван, по нему в новой системе координат не может идти поток. В то же время в связанной сети подобный разрыв не может пройти бесследно. В ответ на операцию разрыва замкнутого пути появляется разомкнутый путь, т.е. появится соответствующая потенциальная переменная, которая до момента разрыва замкнутого пути была нулевой.  И наоборот, если какая либо потенциальная переменная обращается в ноль в новой системе координат, т.е. задано ограничение на потенциальную переменную, то это означает появление замкнутого пути и появление соответствующей потоковой переменной. Взаимосвязь между потоковой и потенциальной переменной может проявляться посредством отражения природы элемента сети и характером воздействия на него. В случае стационарной взаимосвязи между переменными, каждый элемент может характеризоваться некоторыми константами, имеющими природу сопротивляемости движению или воздействию или, обратной ему величины - пропускной способности транспортного канала. Если воздействие имеет потенциальный характер, то ответная реакция на это воздействие - поток. И наоборот, если воздействие имеет потоковый характер, то реакция на это воздействие будет сформирована в виде разности потенциалов, при условии что канал не идеальный. Естественно, что феноменологическая природа элемента сети для каждой предметной области может иметь семантические особенности и специальный характер взаимосвязи между потоковыми и потенциальными переменными. Вмести с тем опыт, приобретенный в изучении физической природы различных явлений, подсказывает о глубоких аналогиях, которые обнаруживаются в описании, построении и преобразовании ее моделей.

наложены внешние воздействия, и эти воздействия могут иметь как потоковую, так и потенциальную природу. Потоки могут быть входными или выходными и действовать на сеть через ее границы (узлы). Иначе говоря, в каждом узле транспортной сети может быть задан некоторый приток или расход ВЭИ, который мы обозначили - J" . Если внешний поток <г > С¹, то он является источником, если поток О" < С¹, то внешний поток выполняет функцию потребления, если j" = С¹ то в узле имеется простая точка разветвления. Суммарная производительность источников, должна совпадать с суммарным расходом потребителей. Потенциальное воздействие также может быть входным или выходным и приложенным к паре узлов сети. Воздействия, характеризующиеся внешними потоковыми и потенциальными переменными, формируют дополнительные потоки и разности потенциалов, возникающие на ветвях сети, которые также как и внутренние переменные подчиняются законам преобразования, вытекающим из структурных (топологических) свойств сети.

(прихода или расхода). Сам источник потенциала подобно э.д.с. и генератору в электрических сетях может находиться в двух состояниях: активном и пассивном. В активном состоянии он генерирует "приток ", задаваемый в виде потенциала ВЭИ подводимого в точку. В пассивном он отбирает часть ВЭИ "расход", т.е. отбирает часть потенциала.  Для транспортной сети это означает, что в пассивном состоянии потенциал формирует затраты мощности на каждую единицу протекающего по данному элементу потока ВЭИ. Одновременно сеть действует на этот элемент через  границы или связи данного элемента с остальной сетью. Тем самым формируется некоторая внешняя по отношению к элементу разность потенциалов, как реакция сети на присутствие или поведение данного элемента. Для транспортной сети эта разность потенциалов может определять, например, добавленную стоимость, которую приобретает единица товара в результате ее транспортировки по данному пути.

Модели элементов в сети

В системах транспортировки ВЭИ, моделируемых потоковыми сетями можно выделить различные элементы. Всегда можно выделить входные и выходные каналы, транспортные каналы, накопительные элементы. При занятости выходных каналов, потоки ВЭИ вынуждены ожидать своей очереди на потребление ВЭИ в накопительных элементах (складах, устройствах накопления информации, емкостях ...). Любую такую сеть можно представить состоящей из множества последовательно связанных накопительных элементов (НЭ) и потоковых элементов (ПЭ), входных и выходных потоковых и\или потенциальных воздействий.

Формируемые и передаваемые некоторым источником ВЭИ могут иметь партионный характер: партия товаров, пакеты информации определенной длинны, тонны вещества и т.п. Потоки, поступающие в узлы (НЭ) проходящие по пути НЭ→ПЭ→НЭ в виду ограниченной пропускной способности, производительности каналов испытывают сопротивление, в результате чего ВЭИ накапливаются в НЭ, ожидая своей очереди на передачу, поставку. Если говорить о производительности потоковой сети, то ее можно охарактеризовать количественным показателем, например, объемом ВЭИ переданным от поставщика к потребителю в единицу времени. Время транспортировки ВЭИ от поставщика к потребителю может служить характеристикой качества передаваемой информации, вещества или энергии по сети. Если транспортировать через сеть определенный объем ВЭИ с определенной скоростью, то при этом будет затрачиваться определенная работа. На передачу с некоторой скоростью и в заданных объемах ВЭИ от отправителей к потребителям по каналам транспортировки потребуется сделать затраты, поэтому общий объем затрат по всей совокупности каналов может служить критерием оценки экономической эффективности потоковой сети.  Сеть можно анализировать в различных контекстах или как говорят метриках, инвариантными останутся методы описания, построения и преобразования сети, ориентированные на получение требуемого результата.

Построим инвариантную модель потокового (контурного) элемента вырванного из сети. Для этого по аналогии с электрическими сетями возьмем некоторый путь и рассмотрим его как контурный элемент с внутренним воздействием и внешним воздействием со стороны сети. В таком случае мы придем к соотношению где:

x - поток внутренний (поток ВЭИ по замкнутому пути ветви);

b - поток внешний (то, что должно отправляться или потребляться, поток в узле);

c – внутреннее потенциальное воздействие. Его интерпретация для разных предметных областей: затраты на транспортировку единицы товара по данному пути, накопления в канале, подводимый источник напора или напряжения т.п.;

y – внешнее потенциальное воздействие: затраты, поставщиков и потребителей, накопления в узлах, давление или напряжение в узлах;.

z – аналог сопротивления движению среды по сети.

Понятие сопротивления приобретает разный смысл в многообразии постановок задач для разных предметных областей.

В сетях связанных с передачей ВЭИ (z) - определяется инструментами измерения отношения c\x. Для каждой предметной области это отношение будет определять некоторое свойство канала транспортировки. Если c - это затраты в рублях, а x - это потоков товаров измеряемый в тоннах/ в день, z - будет выражать стоимость транспортировки единичного потока товаров. Если c - это число пакетов информации (или инфцугов), а x -информационный поток выраженный в пакетов\сек, то z - может отражать временную задержку в передаче по каналу передаваемой информации. Если c -напор, равный давлению, подводимого в точку в канале гидравлической цепи, x - объемный поток, например, воды, то z - это гидравлическое сопротивление, которое, вообще говоря, нелинейно зависит от скорости движения жидкости.

Различным постановкам задач, связанных с транспортировкой ВЭИ, может быть дана различная интерпретация в зависимости от инструментов измерения потоков и потенциалов. Поэтому очень важно понимать, что унификация процессов описания, построения сетей не отменяет задач более точного представления моделей потоковых и потенциальных элементов и связей между ними.

Будем рассматривать задачу оценки стоимости транспортировки по сети потоков товаров, для которой параметры x,c- можно отнести к перевозчику который несет затраты на перевозку, а параметры b,y -к поставщикам и потребителям, которые должны оплатить ему эти расходы, т.е. принести доход.

Поведение сети из n- несвязанных между собой потоковых элементов, вырванных из сети, можно представить следующим образом:

yj 4- hJ ) = fr . +                                                             (74

Здесь:          задаваемые параметры воздействия на элементы транспортной сети, а         определяемые параметры (отклик и реакция). В транспортных задачах матрице можно придать:

• -    диагональный вид, в этом случае каналы транспортировки ВЭИ рассматриваются как независимые,

• -    не диагональный вид, в этом случае можно рассматривать задачи с взаимовлиянием каналов.

Данная система уравнений является полной в смысле воздействующих величин и откликов и представлена в ковариантной форме. Ей можно придать и контравариантную форму, разрешая уравнения относительно контравариантных переменных:

(7) где:       дважды контравариантный геометрический объект - квадратная матрица, аналог проводимости в электрической сети;                . В задачах транспортной сети проводимость будет означать пропускную способность транспортного канала (может измеряться в количестве товаров, информации передаваемых по каналу в единицу времени). В остальном уравнения (7) содержат задаваемые величины и определяемые параметры те же , что и для уравнений (6).

Элементы транспортной сети можно параметризовать двойственным образом, выбрав в качестве переменных параметров потенциальные переменные -   . Тогда уравнения, например (7), можно записать относительно задаваемых и определяемых параметров в том же виде:

(7а)

Отличие состоит лишь в том, что здесь      являются переменными параметрами, которые носят ковариантный характер и на которые накладываются ограничения (связи, аналог второго закона Кирхгофа), а поток      представляют собой вектор реакции связей, возникающий в ответ на вводимые ограничения. Здесь определяемыми переменными будут - потенциальный доход, который получит транспортная система с каждого отправителя и потребителя.

Поскольку в данном варианте моделирования сетей мы не рассматриваем переходные процессы, которые могут существовать в элементах системы, то и модели рассматриваемых элементов у нас носят алгебраический характер инвариантный относительно времени.

Рассмотрим склад или буфер как накопительный элемент, связанный с поставщиками и потребителями посредством каналов транспортировки ресурса. Выделим его из сети. В этом случае воздействием будет внешний поток - b , а откликом потенциальные затраты - y, пропорциональные некоторой пропускной способности склада - Y (поток товара, которое может поступить на склад за единицу затрат). Для склада, как потенциального элемента сети, можно записать соотношения, которое характеризует данный накопительный элемент. Соотношение должно включать появление внутреннего потока - x на складе, который образуется в результате связывания НЭ потоковыми каналами и затрат c - возникающих в связи с прохождением товара через склад (предлагаемая модель и интерпретация характеристических параметров модели накопительного элемента не единственна). Модель некоторого НЭ с индексом (а) можно представить следующим образом:

Если в несвязанной сети существует i= 1,2,...,m ; таких независимых НЭ, то для этого множества элементов можно записать систему инвариантных уравнений:

(9) здесь : k,i= 1,2,...,m;

Поскольку НЭ находятся в узлах сети, то число этих элементов равно числу узлов. Уравнениям (9) можно придать ковариантную форму, разрешив их относительно ковариантных переменных где:                       .

Сравнивая между собой уравнения описывающие поведение контурных и узловых элементов в сети (6),(7),(9),(10) можно заключить, что они носят инвариантный характер. Поэтому в сети можно рассматривать сразу все множество контурных   и узловых

(накопительных) элементов, число которых будет (n+m), а различать их можно придав элементам определенные идентификационные номера и параметры (постоянные и переменные).

Мы не будем останавливаться на доказательстве инвариантности, а также контравариантности и ковариантности отношений для моделей базовых элементов транспортной сети, а перейдем к вопросам, связанным с преобразованиями геометрических объектов, входящих в эти отношения.

Основные преобразования потоковых и потенциальных переменных в транспортной сети

Будем рассматривать поток как контравариантный геометрический объект первого порядка (вектор) и обозначим его                        Закон прямого и обратного преобразования контравариантного вектора потока определим следующим образом (далее в выражениях по повторяющимся индексам выполняется операция суммирования):

yS = c^syJ ■                                                            Г1Л

()

;                                                                                       (12)

иначе

(11а)

(12а) где: j,s = (    );   – символ, отличающий новую систему координат от исходной системы координат;    – квадратная матрица прямого преобразования вектора потока ВЭИ из исходной в новую систему координат;          - квадратная матрица обратного преобразования вектора потока ВЭИ из новой системы координат в исходную систему координат;

Между геометрическими  объектами                 существует  отношение ортогональности:

(13) где:

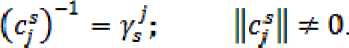
Мы определили объект прямого     и обратного       преобразования, при этом никак не ограничивали значения элементов матриц преобразования.       Для     сетевых структур эти элементы имеют следующие значения:

{-1,0,1}. Тем самым мы определяем интересующий нас класс моделей предметных областей структурные свойства которых укладываются в сетевое представление.

Введем преобразование координат следующим образом:

! Л р — rip X                                                                       .

™ ^T ,Агг.„г„                                  J ’ где: j,s = 1.....n; Лд = ИТТТх = .V - 1 .V - .'/i; .< = :J :

Здесь         потоковые координаты принятые за независимые координаты

(свободные переменные, степени свободы); m=M - число независимых ограничений (уравнений связи); N- число степеней свободы, в принятых обозначениях они совпадают с некоторыми выбранными координатами вектора ; - символ Кронекера; коэффициенты преобразования выбраны так , чтобы они совпадали с коэффициентами ограничений (C) в прямой задаче:

и, следовательно , правые части уравнений (С) должны совпасть с представлением вектора потока в новой системе координат:

Таким образом     результат преобразования вектора потока в новую систему координат -контравариантный вектор. Ограничения (14) в прямой задаче линейного программирования могут быть представлены в новой системе координат просто :

^k2                               '*'3'*   Хч^ "4*Adf ...... к где:

Равенство (17) записано для новой системы координат. Оно сохраняется для произвольной системы координат, поэтому его можно представить в исходной системе координат, используя закон обратного преобразования контравариантного вектора.

Используя закон обратного преобразования потокового вектора (12а) и зная его значения в новой системе координат      можно определить значения в исходной системе координат:

;

где:

Разложим преобразование (18) по подпространствам, получим:

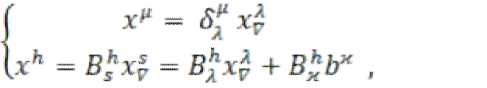
(18а)

где: h, =                      , =                       ;        - символы Кронекера.

Таким образом, если известно значения вектора     в новой системе координат, то можно определить его значение в исходной системе координат.

Ниже представлены законы прямого обратного преобразования потенциальной (ковариантной переменной) переменной:

= qp                                             .

=           ;        =           ;

(18b)

где: i,s = 1,^,n; Л='1 .\"j; ; x = .V - 1 _\ —.Vj:

Объекты        , выбранные в соответствии с равенствами (15) и (17), полностью характеризуют пространство - структуру сети и, вместе с тем, законы преобразования потоковых и потенциальных переменных из исходной системы координат в новую систему координат и наоборот. В выбранном варианте    - строки объекта перечисляют - независимые потоковые переменные;     -строки объекта перечисляют переменные, входящие в  -уравнение связи с соответствующим знаком;      -    столбцов объекта перечисляют переменные входящие в -ый замкнутый путь ;    -    столбцов объекта перечисляют переменные, которые входят в -ый разомкнутый путь.

Такого рода объекты осуществляют операции преобразования различных геометрических объектов накладываемых на сеть. Множество допустимых преобразований сети можно разделить на следующие категории :

• •    преобразования чисто контурной сети (т.е. сети состоящей только из элементов, образующих замкнутые пути);

• •   преобразования чисто узловой сети (т.е. сети состоящей   из элементов

• о бразующих только разомкнутые пути); преобразования связанные с выбором независимых замкнутых путей и разомкнутых путей;

• •    преобразования, связанные с объединением независимых элементов в сеть;

• •    преобразования перехода от одной построенной сети к другой.

И за каждым преобразованием разомкнутых и замкнутых путей стоят преобразования контравариантных (потоковых) и ковариантных (потенциальных) векторов, посредством которых мы параметризуем геометрическое пространство сети. Таким образом, если связать с каждым замкнутым путем переменную , то преобразование замкнутых путей будет связано с преобразованием данного вектора. Если с каждым разомкнутым независимым путем связать потенциальную переменную      (разность потенциалов), где i=1,...,n; то преобразование разомкнутых путей будет связано с преобразованием ковариантного вектора

V.

Модели пространства транспортной сети

Сеть можно всегда разделить на два независимых подпространства: одно подпространство характеризует поведение контурной части сети, другое подпространство будет характеризовать поведение ее древовидной структуры, узловой части сети. То есть необходимо выбрать такие хорды топологической структуры сети, редукция в ноль которых приводит к разорву замкнутых путей и древовидной структуре, обеспечивающей минимальную стоимость транспортировки. По сути, работа, например, симплекс-метода для транспортной задачи заключается в организации процедуры поиска древовидной структуры сети, на которой f(x) = f( ) -приобретает минимальное значение.

Последовательным преобразованием системы координат, параметризованной векторами                  , (где: =             =                  ) в новую систему координат с другими координатами                    , можно получить функции f(x) или g(x), которые изменятся в сторону своего экстремума. Общее число независимых потоковых и потенциальных переменных будет оставаться инвариантным.

Для сети можно предложить два способа задания уравнений связи между потоковыми переменными, которые, тем не менее, приводят к одним и тем же моделям пространства. Первый способ рассматривает уравнения связи в виде законов аналогичных первому или второму закону Кирхгофа. В этом случае уравнения связи для потоковой переменной в новой системе координат представляются в виде :

— Д^к¥^ — П                                                     П Re')

(18с)

а внешнее воздействие в новой системе координат    является заданным.

Второй способ позволяет представлять уравнения связи в виде равенства:

Yx _ Ди: Yj = КИ

(18d)

=

В этом случае внешнее потоковое воздействие принимается равным нулю, а значение     принимается равным   . И в том и другом случае мы придем к одним и тем же уравнениям, которые могут быть представлены в ковариантном и контравариантном виде [3]:

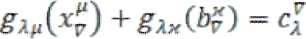
(i)

^<+^) = 4+ у*

г = crWc^ + H*fc^F + уП

(ii)

I й? - gh^ (c^) + ^(с^ + Ух)

где:                               ;                                 ;                                 ;                                 ;

;                                                            ;                                                          ;                                                           ;

;                 ;                    ; , =1,...,N; ,h =N+1,...,N+M.

Уравнения (i) и (ii) позволяют рассчитывать неизвестные потоковые и потенциальные переменные при заданных входных потоковых и потенциальных воздействиях с учетом заданных параметров каналов, а также ограничений 18с или 18d. Использование уравнений (i) или (ii) расширяет возможные постановки прямых и обратных задач анализа транспортных сетей, и изменяет задачу оптимизации структуры сети. Полученные изменения касаются ограничений, накладываемых на потоковые или потенциальные переменные, которые вытекают из полученных соотношений (i) и (ii). Для каждого варианта характеристик каналов, структуры замкнутых и открытых путей можно получить частное распределение транспортных потоков, которые будут удовлетворять заданным ограничениям в прямой задаче,  или определить затраты поставщиков и потребителей в двойственной задаче. Для каналов имеющих единичные характеристики сопротивления, кроме изменения выбора независимых и зависимых потоковых координат, структуру сети можно изменить при помощи задания больших величин сопротивления по каналу. Там, где большое сопротивление на потоковом элементе, движение потока будет минимальным. Таким образом, можно подобрать такую древовидную структуру, обеспечив ее элементы единичными сопротивлениями (остальные сопротивления будут иметь большое число), при которых будет обеспечен min f(x). Как найти оптимальное решение? - остается самостоятельной задачей. Покажем, что транспортная задача в тензорно-геометрической постановке имеет достаточно эффективные методы построения оптимального решения.

Рассмотрим сначала идеализированный вариант решения транспортной задачи не учитывающий потери в транспортных каналах. Представляется, что применяемые методы описания и алгоритмы решения могут использоваться и для более общих постановок задач, где каналы не идеальны, а    ,   могут иметь характер линейного преобразования.

Тензорная интерпретация критериев оптимальности

Рассмотри критерии оптимальности и ограничения с тензорной точки зрения: f(x)=                          (A)             g(y)=(B)

В тензорных обозначениях их следует переписать следующим образом: f(x)=                     (A1 )           g(y)=(B1)

(C1)(D1)

где: j=          =.

В выражениях (А) и (В) отсутствует понимание  - в каких системах координат представлены геометрические объекты и с какими законами преобразования они связаны. В выражениях (А1) и (В1) функции представлены геометрическими объектами разной природы, одни объекты – потоки контравариантные:        , а другие объекты – разности потенциалов:             – ковариантные. Данные объекты имеют разные законы преобразования. Обратим внимание, что функции записаны в разных системах координат: f(x) в исходной системе координат, а g(y) в новой системе координат.  Второе на что необходимо обратить внимание это то, что согласно (17)        это контравариантный потоковый вектор, представленный в новой системе координат. Поэтому, согласно обратному тензорному признаку (в силу того, что В1 в каждой системе координат это скаляр)      ковариантный вектор, который также представлен в новой системе координат

. Более правильная запись критерия оптимальности для двойственной задачи совпадает с (В1).

Заметим, что если вернуться к каналам транспортировки с сопротивлением и определить   в соответствии с равенством (6) как

, то критерий минимизации f(x)=               будет определять уравнение рассеяния мощности в потоковой сети, который надо минимизировать при ограничениях (i).

Если определить уравнение для потока в виде            , умножить его на и полученное выражение преобразовать в новую систему координат, то получим

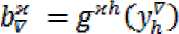
и тогда g(y)=        =                 будет определять уравнение мощности для потенциальной сети, записанное в новой системе координат, которое надо максимизировать при ограничениях (ii) .

Преобразуем (А1) в новую систему координат. Для этого подставим вместо вектора его представление в новой системе координат, получим

f(x)=(19)

где:                                 .(19a)

Разложим составляющие функции f(x) по подпространствам. При этом, учтем равенство (17) и  равенство          . Оптимальное решение достигается в одном из подпространств, для которых контурные переменные обращаются в нуль:.

Действительно, если транспортный поток будет двигаться по какому либо замкнутому пути, то не все потоки имеющиеся на входе, попадут на выход, и значит нарушится одно из условий решаемой задачи: суммарные запасы и суммарные заявки должны быть равны между собой. Тогда

f(x )=                                                                                  (20)

д,                                                            .

Мы видим, что если критерии оптимальности рассматривать в одной системе координат, то их оптимальные значения совпадают. Координаты вектора     - можно рассматривать как подпространство потенциальных переменных, связанных с независимой парой узлов на сети. Поскольку количество узлов в сети на единицу больше числа независимых уравнений связи, то одно из уравнений связи (С1) можно отбросить. В результате индекс -пробегает значения =                  , где M+1=m (число узлов).

Это эквивалентно тому, что одну из потенциальных переменных , связанную с отбрасываемым узлом можно принять равным нулю. В этом случае все другие значения потенциальных переменных базисного множества путей будут рассматриваться относительно данного нуля, т.е. будут выражать подмножество значений разностей потенциалов, которые и принимаются за потенциальные переменные.

Поиск оптимального плана при использовании критерия минимизации

Рассмотрим уравнение связи для потоковых переменных в виде

=    , где - известное внешнее потоковое воздействие.

Выбор начального множества независимых и зависимых переменных будем определять одним из известных методов или одним из алгоритмов построения дерева на заданной структуре сети [4,5].

При параметризации сети потоковыми переменными                =

=                 , N – независимых переменных будет характеризовать хорды сети, а M

• - зависимых переменных будет характеризовать ветви, определяющие дерево сети.

Допустимый набор зависимых переменных для потоковой сети является базисным для задачи линейного программирования . Независимые переменные - хорды, замыкают переменные характеризующие ветви дерева до замкнутого пути, т.е. образуют независимые замкнутые пути, причем единственным образом.

Замена одного базиса другим, который приводит к уменьшению f(x), может быть выполнена путем анализа - замкнутых путей, которые можно получить замыканием соответствующих независимых переменных - хорд рассматриваемого на каждом шаге дерева. Суть этого анализа сводится к поиску такой хордовой переменной, которая максимально уменьшит значение линейного функционала, и поиску такой базовой переменной, которая в силу ограничений, должна выйти из базиса.

Рассмотрим критерий минимизации прямой задачи транспортной сети в новой системе координат и разложим его по подпространствам:

f(x )=                                                                                       (21)

где: =            =                  ,        базовые потоковые переменные в новой системе координат;      независимые переменные в новой системе координат;

поскольку решение ищется в подпространстве, когда все контурные переменные обращаются в нуль.

Рассмотрим обратное преобразование (18), (18а), с помощью которого можно определить значение потокового вектора базисных переменных в исходной системе координат

,                                                                                             (22)

здесь:   - заданные внешние потоковые воздействия;   - обратное преобразование.

Выражение (22) можно разложить по подпространствам:

,

(23) где:   - значение вектора потоковой переменной в исходной системе координат; учтено, что

=0.

Из соотношений (23) видно, что значения вектора базисных переменных полностью определяются   геометрическим   объектом

Поэтому, решение задачи определения min f(x ) напрямую связывается с построением такого преобразования    при котором обеспечивается min      .

В начальной точке рассмотрим единичное потоковое воздействие, которое можно задать на хордах транспортной сети         и его влияния на значения критерия (21):

f(x )=                                                                                          (24)

начальное значение f(x)

Если среди всех      найдется такое, что         , то оно потенциально может уменьшить значение линейной функции f(x). Поэтому, сначала определим, а затем выберем среди всех                  наименьшее из отрицательных значений. Обозначим эту переменную фиксированным индексом - a, т.е. . Напомним, что - ковариантный объект (сумма затрат по ветвям - ого замкнутого контура, взятых со своим знаком) определяемый по закону преобразования:

(25) где:     затраты по путям, входящим  замкнутый контур определяемый -ым столбцом матрицы .

Введем в рассмотрение потоковую переменную , представляющую собой хорду некоторого а-го замкнутого пути. Эта переменная является лишней, поэтому ее введение потребует пересмотра потоковых базисных переменных, входящих в замкнутый путь, одна из базисных переменных должна будет уйти. Будем постепенно увеличивать значение , тогда, в силу уравнений связи (18c), будет происходить нарушение существующего баланса между поставщиками и потребителями. Чтобы сохранить баланс в каждом узле сети, нарушенный хордой , необходимо пересчитать значения базисных потоков, полученных на предыдущей итерации. Для этого мысленно к потокам ветвей входящих в контур будем добавлять величину    , если данный поток имеет знак (+) и вычитать аналогичную величину, если поток имеет знак (-). Поскольку значения базисных потоков должны быть всегда положительными, то та базисная переменная, которая раньше всех обратиться в ноль, будет претендентом на выбывание. Эта та переменная из множества, которые входят в контур со знаком (-), имеющая минимальное значение.   Таким образом, можно не пересчитывать новые значения , лишь определить ту ветвь, ту переменную, которая выйдет из базиса. Теперь мы имеем новую переменную    , которая войдет в базис и ту базисную переменную, которая выйдет из базиса.

Подобные действия приводят к построению объекта      , в котором скользящие индексы h1 и 1 пробегают новые значения индексов потоковых базисных переменных. В соответствии с (23) можно определить значения новых базисных переменных и функции:

_ D filial   J Fil                                                                  r-x^x f^x )= f^ f(x )=

Для нового объекта      можно проделать ту же логическую последовательность действий и она будет следующей итерацией, по изменению объекта      в объект      .

Итерационный процесс закончится когда все         , где b - фиксированный индекc, обозначающий количество итераций.

Поиск оптимального плана при использовании критерия максимизации для двойственной транспортной задачи

Рассмотрим критерий максимизации для двойственной задачи транспортной сети и определим его значение в исходной системе координат:

g ( y )=                                                                                        (27)

где:                                              ;                              и                              , соответственно независимые и зависимые потоковые переменные, определяемые в соответствии с преобразованиями (22) или (23) в подпространствах исходной системе координат;

соответственно независимые и зависимые потенциальные переменные, представленные в подпространствах исходной системе координат.

Мы здесь точно также допускаем, что существует такой метод, который позволяет определить начальную вершину и тем самым определить значение вектора базисных переменных в исходной системе координат в соответствии с выражениями (22) и (23). Кроме того, должны выполняться уравнения связи для двойственной задачи:

Я;

Из уравнений (28) в начальной точке можно определить сначала    , а затем

^(Л^)"1 =уя

В этой же точке рассмотрим единичное потоковое воздействие, которое можно задать на хордах транспортной сети        и его влияния на значения критерия (27):

g(y)=                                                                               (30)

Если среди всех     найдется такое, что        , то возможно увеличение значений линейной функции g(y). Поэтому выберем среди всех                    наибольшее из положительных значений. Обозначим эту переменную фиксированным индексом - α, т.е.   .

Напомним, что - ковариантная потенциальная переменная определяющая разность потенциалов узлов транспортной сети, принадлежащих α - ветви (пути). Будем увеличивать значение соответствующей потоковой переменной - . Введение нарушает балансовые соотношения, определяемыми уравнениями связи. Поэтому необходимо скорректировать переменные . Рассмотрим контур, определяемый столбцом матрицы и выберем в нем все отличные от нуля элементы, для всех положительных элементов определим                     . Тогда значение переменной min { } первое обратиться в нуль. Именно данная потоковая или соответствующая ей потенциальная переменная должны уйти из базиса.

Таким образом, мы теперь знаем индекс переменной, которая должна войти в базис и индекс переменной, которая должна уйти из базиса. Это дает возможность изменения матрица прямого преобразования     и построения новой матрицы      . Следовательно, можно построить матрицу обратного преобразования В;7 = '. .-/-" , по соотношению (26) определить новые значения переменных у-. Так заканчивается первая итерация. Итерационный процесс заканчивается тогда, когда все ": < С1 и значения искомой функции не могут быть увеличены.

Для проверки оптимальности плана в симплексном методе иногда используются экономические оценки 2 = у — у , которые делаются для хорд рассматриваемой транспортной сети. Экономическая оценка показывает, на сколько денежных единиц изменяться транспортные издержки от загрузки данного пути единицей ВЭИ. Если оценки не отрицательные, т.е. 2 > 0 , то план оптимальный и остается подсчитать транспортные расходы. Иначе переходят к следующему анализу. Из отрицательных оценок 2 ^ С¹ выбирают оценку с максимальным значением, по абсолютной величине, которая соответствует определенной хорде. Тогда данную ветвь - переменную вводят в число базисных переменных, т.е. строят цикл по загруженным путям с началом в выбранной хорде и перераспределяют поставки так, чтобы баланс сохранился. Для этого ветвям входящим в цикл приписывают чередующиеся знаки (+) и (-), соответственно тому как они направлены в цикле: от поставщика или к поставщику, хорде приписывают знак (+). На минусовых ветвях отыскивают наименьшую величину поставки ВЭИ, т.е min {.у- }, который и "перемещается" по ветвям замкнутого цикла, т.е. прибавляется к транспортным потокам имеющим знак (+) (включая хорду) и вычитается из транспортных потоков в ветвях со знаком (-). Следовательно, ветвь min {.у- }, редуцируется в ноль и уйдет из базиса. Значения остальных переменных переписываются. Т.о. получают новый улучшенный план транспортных потоков, для которого транспортные издержки изменяются на величину ■_ 2 - 2i'.'2 : .У ■ ;"

Преобразования порядка независимых и базисных переменных

В задачах построения преобразований из одной системы координат в другую довольно часто возникает задача построения преобразования, в котором переменные изменяют последовательность. Подобная ситуация возникает, например, когда приходится заменять базисные переменные на независимые переменные в задаче линейного программирования. Вместе с тем, все тензорные преобразования записаны для геометрических объектов, индексы которых пробегают строгую последовательность целых чисел. Что происходит с матрицами прямого и обратного преобразования и самими контравариантными или ковариантными векторами, когда порядок следования координат изменяется. Рассмотрим преобразование координат контравариантного геометрического объекта: х^ - характеризующего транспортные потоки ВЭИ х^ — ^у х^" ; где: s,j =1,...,n;

Представим данное преобразование в виде (14), в котором выражена связь между новыми и старыми координатами транспортной сети

{лс5 — А^ х^

я                                        <311

~-х _ 3^' _v" _ Д^хуЛ i Ax_vh _                                 ^х *

где: Л, 11 =       ,h =(/V + l.jV+Я);^ = 5^

N-число независимых координат (степеней свободы);

M- число зависимых координат (базисных переменных);

n=N+M - число транспортных путей.

Рассмотрим как изменяться преобразования в случае, если порядок следования переменных X иX будет изменен на примере потокового вектора шестимерного пространства xi , где i =1,...,6. Пусть на данный вектор накладывается M=3 независимых ограничений, тогда число зависимых переменных будет равно 3 и число независимых переменных N=3. В соответствии с нашими обозначениями индексы независимых координат пробегают значения Л,М =1,...,3; индексы зависимых координат пробегают значения X,h = 4,...,6. Допустим, что эта последовательность нарушена и независимыми являются следующие координаты: X L-^" j ^^ j ^^ , а зависимыми координатами (базисными) следующие: X L-"^- j -^ j ^ j. Введем в рассмотрение прямое преобразования в соответствии со следующей таблицей 1.

Табл. 1. Прямое преобразование

		: г	X*		Х^	Х^
Х-'	хэ	У z	х1	х2	х	х6
s)	^3	S?	•^L	^2	V5 J-L	J6

Данное преобразование можно записать иначе: =       ■ и построить для него обратное преобразование:

-yj = 5^ х^ ■                                                                     ИЗ')

где: l,j=1,...,n;

Ниже представлены явные значения приведенных матриц преобразования:

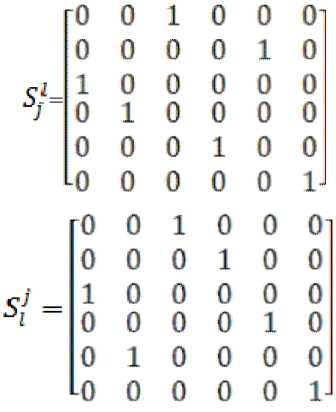
Используя преобразования типа (32) и (33) можно построить законы преобразования, связывающие координаты нового представления потокового вектора и старого, но имеющего другой произвольный порядок обозначения:

Л^ с/ _ 45                                                          П6х где:                                                                     ;

объекты второго порядка прямого и обратного преобразования;

s,l,j=1,...,n; (•) - символ обозначающий объекты с упорядоченным координатным базисом.

Используя принятые обозначения и полученные объекты   (36), (37) можно представить законы прямого и обратного преобразования для нового координатного базиса:

Х 5" — ДЗ -^2

А# " *3 ^Р

Геометрические объекты    и    будут иметь всегда следующую структуру

J5 —

"6?

Г 6АLs*r

о

О

"•и.

Поэтому, если известно     то определить

будет достаточно просто :

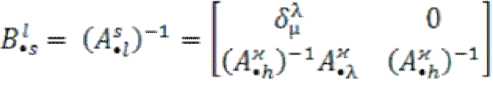
При помощи преобразований типа (32), (33), (38), (39) можно изменять порядок переменных таким образом, что в используемых уравнениях он будет представлен всегда единообразно . Поэтому всегда индексы , будут пробегать последовательно значения от 1до N, где N - число независимых переменных, а индексы    ,h будут пробегать последовательно значения от N+1 до N+M, где М - число независимых уравнений связи. В задачах линейного программирования решаемых при помощи тензорных преобразований подобный прием дает возможность заменять зависимые и независимые переменные. Например, на каждой итерации приходится заменять одну из потоковых переменных характеризующих ветвь дерева на независимую потоковую переменную - хорду, и строить другое дерево транспортных потоков, которое приближает нас к оптимуму. Переход от одной структуры транспортных потоков к другой есть построение преобразований типа (36), (37).

Пример

Представим тензорную модель транспортной сети состоящей из n=12-контурных элементов в системе координат определяемой прямым преобразованием (14) и обратным преобразованиям (18) и (m-1) = 6 уравнениями связи (17) где m- число узлов сети. Будем рассматривать построение модели на конкретном примере транспортной сети состоящей из трех поставщиков A,B,C в которых производится отгрузка товара и четырех потребителей O,P,Q,T, которым осуществляется доставка товара в соответствии с их возможностями и потребностями представленными вектором в таблице 2. Движение товара по каждому пути связано с затратами приходящимися на каждую единицу перемещаемого товара, они представлены также в таблице 2. При заданных исходных данных можно поставить задачи отыскания таких или которые обеспечат выполнение условий

f(x)=                     (A2 )           g(y)=                   (B2)

(C2)                                (D2)

где: j=          =                  ; n=12; M= (m-1)= 6; N=n-m+1=6;

представление   в подпространстве древовидной структуры сети;

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление»

www.rypravlenie. ru

том 8 № 2 (15), 2012, ст. 5

Ул – представление потенциальной переменной У/ , в подпространстве древовидной структуры сети, т.е. в новой системе координат; (C2),(D2) – ограничения, записанные соответственно в новой системе координат.

Табл. 2. Построение модели на конкретном примере транспортной сети

с 1

с 2

с 3

с 4

с 5

с 6

с 7

с 8

с 9

с 10

с 11

С12

1

2

5

3

1

6

5

2

6

3

7

4

Ьр — "1

bl = ь2

bl — b3

Up — Ы4

60 (A)

120 (B)

100 (C)

20 (O)

110 (P)

40 (Q)

110 (T)

Запишем уравнения связи для каждого узла данной транспортной сети, получим:

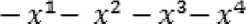
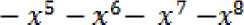
+ 60 = 0

+ 120 = 0

V9— V10 — -Г11 — V12 Л- Л-         Л-        Лг

+100 = 0

Х^               ~Ь Х^             ~Ь х^                  —20 = 0

A-                                     I А-                                      I А- '                         '110 = 0

А-                                    I . Л-                                   I А-                   '40 = 0

+ X8

I А- 110 = 0

Число независимых уравнений (m-1) равно шести, поэтому одно из представленных уравнений связи можно отбросить. Пусть это будет последнее уравнение. Используем уравнения связи для построения прямого преобразования системы координат. Для этого определим, каким либо способом систему независимых и зависимых координат транспортной сети, например

• -    независимые координаты,

• -    зависимые координаты, определяющие базис.

Оптимальное решение ищется в точке подпространства, когда все независимые потоковые переменные обращаются в ноль:         , где =3,4,5,9,10,11. В этом случае сеть формируется древовидная структура сети.

Для того, чтобы было удобнее работать изменим порядок координат:

X11

X^

: 1

X10

X11

X12

V'

х^

X4

xa

x^

X10

X11

x^

Y~

x^

X®

X12

s“

51 D3

52

Si

л4 D9

a10

^ll

s7 ^L

5s J2

C9 J6

CIO a7

s11 “5

J12

В первой строке таблицы задана новая система координат, где потоковые координаты имеют порядок натурального ряда. Во второй строке таблицы 2 сначала расположены шесть независимых координат, а затем шесть базисных координат. В последней строке таблицы показаны отличные от нуля элементы матрицы преобразования    .

Используя соотношение (36), введем прямое преобразование потокового вектора следующим образом т5 — As т11       ч//=1   1?-                                      мп s,l1 =1,...,12;                                                                          (41)

иначе, разлагая вектор по подпространствам, получим

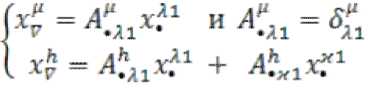
где:     1, = 1,...,6;        1,h=7,...,12 ;

Представим выражение (42) в явном виде, где в правой части представлен результат преобразования (см. (40)):

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление»

www.rypravlenie. ru

том 8 № 2 (15), 2012, ст. 5

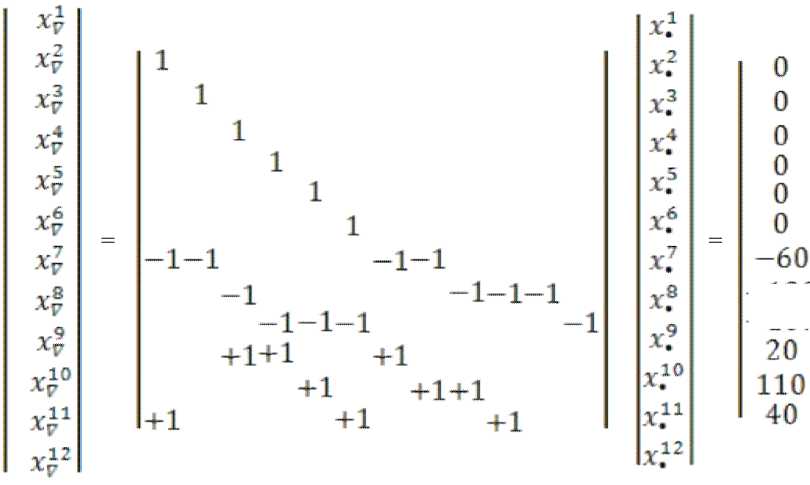
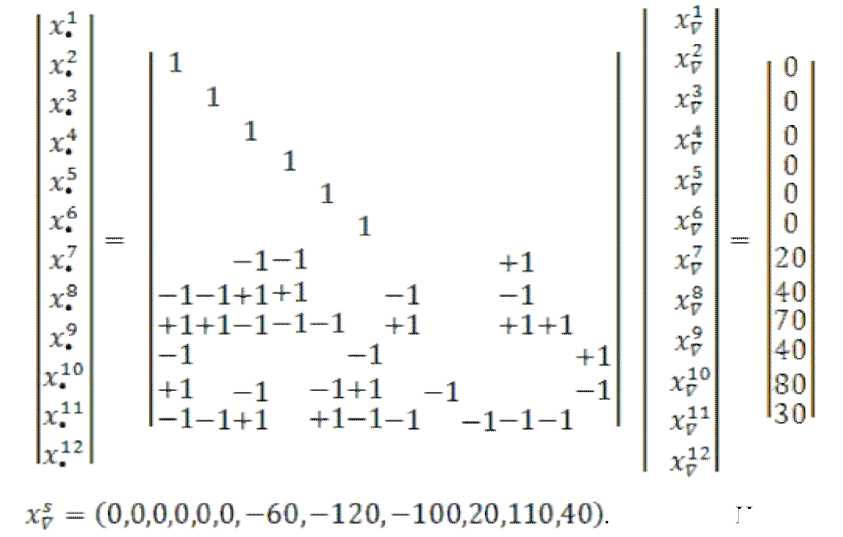
Построим обратное преобразование         =

-120-100

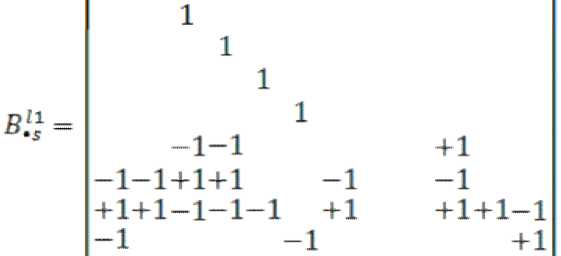
+ 1+1+1 —1™1

с помощью которого определим значения потоков в исходной системе координат.

где:                                                          – заданный вектор.

Вектор в правой части определяет исходное распределение потоков транспортной сети, для которого f(x)=                             0 , где:

Рассмотрим возможность уменьшения критерия минимизации. Для этого определим значения     , где 1=1,...,6; как                   , получим

_ А. С. _ Д. _ 1 . _ С . Л .                                                         _(л<-х

Выберем наименьшее из отрицательных значений         . Оно (предположительно)

в большей степени может уменьшить значение

f(x)=                  =                                                             (47)

где:     образует с ветвями дерева контур, определяемый вектор - столбцом матрицы

(0;0;0;0;1;0;0;0;-1;0;1;-1).

Если постепенно увеличивать значение      , то ветвям, входящим в контур с положительным знаком необходимо добавлять данное значение, а ветвям с отрицательным знаком вычитать данное значение. Это связано с необходимости балансировки потоков, входящих в замкнутый контур. Поскольку потоки должны оставаться положительными, то мы не можем бесконечно увеличивать , а только до минимального значения потока из двух, имеющих отрицательный знак в        min {        } ={70;100} =70. Это значит, что поток     выйдет из базиса. Таким образом, мы пришли к выводу, что поток вводится в базис, а поток х^ из него выводится. Если вернуться к понятиям независимые и зависимые исходные координаты, то они изменятся следующим образом:

7С — ?С у 7С ^ 7С , ?С у ?С у ?с ^ - независимые координаты,

- зависимые, базисные координаты;

Матрица преобразования будет иметь следующий вид:

Поскольку измениться взаимосвязь между координатами исходной -   х-^ и l 2

промежуточной системами координат X, , то изменится обратное преобразование ^; , определим его значения:

Мы не будем останавливаться на алгоритмах получения обратного преобразования от итерации к итерации. Они достаточно просты.

Определим новые значения х, :

где:

значения

Новые

₌ г             = 7Q0

f(x)=                                .

Определим

C;2 = (-l;0;l;4;5;0;)

Минимальное значение из всех

элементов имеет C1 - 1 ;   Теперь можно определить отрицательные элементы столбца

5 J £ = (8,10,12) , и соответствующие ему потоковые координаты, из которых необходимо выделить координату, имеющую минимальное значение: min {70,40,30}=30. Таким образом, мы приходим к выводу, что потоковая координата входит в базис, а потоковая координата x^    выходит из базиса. Если вернуться к понятиям независимые и зависимые исходные координаты, то они изменятся следующим образом:

7C — £ 7C у ?C у ?C у ?C у ?Q i .X-    - независимые координаты, x tx j X" j Л^ j X j X j X ^ - зависимые, базисные координаты;

Определим обратную матрицу        =    :

Вычислим вектор

vt3 — Р13 V5

, где:     • =              :     -      ^ ;    ^    ■ ' ;    , ,    . ,13=1,...,12; получим или если вернемся к обозначениям рисунка, то получим

х^ - (20,10,30,0,0,0,10,110,0,100,0,0,),) = 1....Д2.

Подсчитаем                     , отрицательных значений нет, оптимум найден.

Определим f(x) = С,; ?.'’;" = с ? .Y -" = / y J