Тензорный метод анализа эффективности информационных систем управления бизнес-компаний телекоммуникационной отрасли

Информационная система управления представлена в виде замкнутой структуры однолинейных систем массового обслуживания. Такое представление наиболее полно отражает реальный процесс. Система массового обслуживания является эквивалентом узла информационной сети. Когда структура сети не большая, представленные модели имеют простые решения. Однако уже при численности сети в десять и более узлов решения усложняются из-за большого числа сочетаний и связей между ними. Кроме того, стоит задача синтеза оптимальной структуры информационной сети, что не позволяет сделать теория массового обслуживания. Поэтому для анализа и синтеза информационной структуры управления больших бизнес компаний и уменьшения расчетов предлагается использовать тензорный анализ. На примере продемонстрировано применение тензорного контурного метода анализа для вывода уравнения анализа эффективности управления структуры, состоящей из двенадцати узлов. Каждый узел представлен как отдельная система массового обслуживания, связанная с другими узлами (системами). Суть тензорного анализа изложена в работах Г. Крона [1; 2]. Основные положения использования тензорного анализа для систем и сетей массового обслуживания представлены в работах М. Н. Петрова [3-6].

Согласно правилам тензорной теории [5. С. 27] проведем исследование структуры системы управления биз-нес-компании (рис. 1). Для того чтобы не загромождать рисунок, возле каждой ветви приведен лишь ее номер, который затем подставляется в индексы i соответствующих величин L i и % i .

Определяются параметры структуры исходной топологии:

n = 12 - число ветвей;

U = 9 - число узлов;

K = 1 - число подсетей;

• ( n — k ) = U — K = 9 — 1 = 8 - число узловых пар;

k = n — ( n — k ) = 12 — 8 = 4 -числоконтуров.

Для исследования выбирается координатное представление структуры, более удобное для анализа. Структура примитивной сети получается путем разнесения отдельных систем массового обслуживания (сотрудников) на бесконечное расстояние, т. е. системы не связаны между собой. Структура примитивной 12-контурной топологии, которая будет использоваться в качестве вспомогательной, приведена на рис. 2. Таким образом, представлены две разные проекции одной структуры, включающей 12 систем массового обслуживания (рис. 1 и 2).

Далее требуется описать уравнения состояния геометрических объектов (проекций топологии) и установить их связь. Соответственно для описания эффективности деятельности примитивной топологии предлагается использовать следующие понятия:

• -    % - вектор, компоненты которого представляют собой удельную эффективность каждого узла в соответствующих ветвях (рис. 2). Причем каждый компонент может являться многомерной функцией, учитывающей производительность, достоверность и др.;

• -    Lg - вектор, компоненты которого представляют собой эффективность управления в соответствующих ветвях (с позиции общей задачи управления);

• - N- квадратная матрица размерностью^-строк на ^g-столбцов. Элементы главной диагонали представляют собой значения числа узлов, соответствующей данной ветви (если анализируется один узел, то ^= 1). Ос

тальные элементы матрицы отражают взаимное косвенное влияние систем массового обслуживания друг на друга (использование общих ресурсов и т. д.).

N L

N L

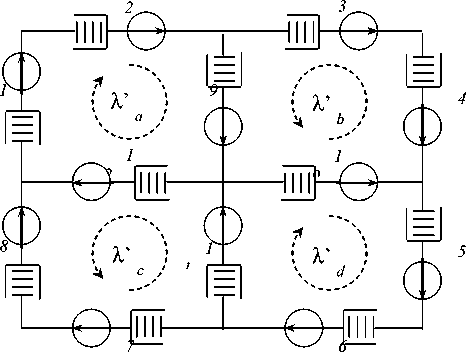
Рис. 1. Исходная контурная структура информационной сети

^N ₁₂ ^L n

^

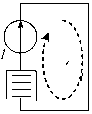
Рис. 2. Структура примитивной 12-контурной топологии

Примем, что в данном примере косвенное влияние между системами массового обслуживания отсутствует, поэтому все недиагональные элементы матрицы N равны нулю.

		Г Lg 1 1		Г% 1 1
		Lg 2		% 2
		Lg з		% 3
		Lg 4		% 4
		Lg 5		% 5
Lg =		Lg 6	% =	% 6
		Lg 7		% 7
		Lg 8		% 8
		Lg 9		% 9
		Lg 10		% 10
		Lg 11		% 11
		. Lg 12 .		_% 12 _
	N и 0      0	0        0	0        0        0        0	0	0         0
	0      N 2,2        0	0        0	0        0        0        0	0	0         0
	0       0        N 3,3	0        0	0        0        0        0	0	0         0
	0      0       0	N 4,4         0	0        0        0        0	0	0         0
	0      0       0	0       N 5	0        0        0        0	0	0         0
N =	0      0       0	0        0	N 66      0       0       0	0	0         0
	0      0       0	0        0	0         N 7,7         0          0	0	0         0
	0      0       0	0        0	0       0       N,       0 8 8	0	0         0
	0      0       0	0        0	0        0         0        N 9	0	0         0
	0      0       0	0        0	0        0         0        0	N 10 1	0         0
	0      0       0	0        0	0        0         0        0	0	N 11,11          0
	0      0       0	0        0	0        0         0        0	0	0         N ,272

Если % - удельная эффективность каждого узла, то матричное уравнение состояния примитивной топологии для определения эффективности управления в соответствующих ветвях Lg-вектора, примет вид

Lg = N % .

Соответственно при объединении примитивных структур в контурную топологию для определения общей эффективности работы сети следует воспользоваться формулой

Lg ' = N ' % '.

Таким образом, данное соотношение предлагается в качестве тензора для исследования эффективности деятельности структур управления компанией, так как не изменяется при переходе от одного координатного представления к другому

Так как матрица Lg - диагональная, то эквивалентная система уравнений состояния примитивной структуры получается перемножением соответствующих компонент матрицы Nи вектора % (рис. 2):

Lg 1 = N_v%

^Lg 2 = ^N 2,2 % 2

^Lg 3 = ^N 3,3 % 3

^Lg 4 = ^N 4,4 % 4

^Lg 5 = ^N 5,5 % 5

^Lg 6 = ^N 6,6 % 6

^Lg 7 = ^N 7,7 % 7

^Lg 8 = ^N 8,8 % 8

^Lg 9 = ^N 9,9 % 9

^Lg 10 = ^N 10,10 % 10 ^Lg 11 = ^N 11,11 % 11 ^Lg 12 = ^N 12,12 % 12

Для перехода от примитивной к контурной топологии требуется определить матрицу преобразования. Зададим удельные эффективности в контурной топологии по числу контуров, направления выбранных контурных удельных эффективностей показаны на рис. 1. Выражения удельной эффективности в ветвях примитивной структуры через интенсивности эффективностей в контурах исходной структуре:

	а	: ъ	; с	: d
% 1 =% a	1	0	0	0
% 2 =% a	1	0	0	0
% з =—% b	0	-1	0	0
% 4 =—% b	0	-1	0	0
% 5 =% c	0	0	1	0
% 6 =% c        C "	0	0	1	0
% 7 = -% d	0	0	0	-1
% 8 = -% d	0	0	0	-1
% 9 =% a +% b	1	1	0	0
% 10 =% b +% c	0	1	1	0
% 11 =% c +% d	0	0	1	1
% 12 =% a +% d	1	0	0	1

Транспонированная матрица преобразования:

	1       1       0			0	0	0	0	0	1      0		0	1
C T =	0	0	-1	-1	0	0	0	0	1	1	0	0
	0	0	0	0	1	1	0	0	0	1	1	0
	0	0	0	0	0	0	-1	-1	0	0	1	1

Нахождение геометрических объектов, соответствующих исходной системе. Эффективность управления организаций в целом в контурах исходной системы:

Lg' = C ^- Lg =

110 00

О  О  -  -1о

0   0   0   01

0  0   0  00

0 0 01

0 0 01

10 00

0 - -1 0

0 0

1 0

1 1

0 1

^Lg 1

Lg2

Lg 3 Lg A Lg s

Lg b

Lg !

Lg s

Lg » Lg 10 Lg 11 Lg 12

Lg 1 ⁺ Lg 2 ⁺ Lg 9 ⁺ Lg 12

- Lg 3 - Lg 4 ⁺ Lg 9 ⁺ Lg 10

Lg 5 ⁺ Lg 6 ⁺ Lg 10 ⁺ Lg 11

^- Lg 7 ^- Lg 8 ⁺ Lg 11 ⁺ Lg 12

Значения необходимого числа узлов для эффективного выполнения управления в контурах исходной системы находятся по следующей формуле:

N ' = С ^T NC.

В целях экономии места и трудоемкости применяется правило: при умножении любой матрицы М на диагональную (если такое умножение возможно), эта матрица сохраняет свою размерность, а каждый ее ненулевой элемент умножается на диагональный элемент N jj в соответствующем столбце. Таким образом, после проведе

ния первого умножения:

0      00

0      00

-100

-100

0        I0

0        10

0       0-1

0       0-1

1        00

1              10

0             11

0       01

N 9 9

/V  + /V  + /V + /V

N 3,3 ⁺ N 4,4 ⁺ N 9,9 ⁺ N 10,10

N 10 10

N 1010

N 5,5 ⁺ N 6,6 ⁺ N 10,10 ⁺ N 11,11

N 11,11

N 12,12

N 11,11

N 7,7 ⁺ N 8,8 ⁺ N 11,11 ⁺ N 12,12

Теперь можно найти уравнения состояния исходной структуры (рис. 1). Уравнение состояния исходной сети, записанное в матричной форме имеет тот же вид, что и уравнение состояния примитивной сети:

Lg ' = N ' X '.

Эквивалентная система уравнений для анализа исходной топологии:

Lg 1 ⁺ Lg 2 ^{+ L} g 9 ^{+ L} g 12 =

= ( ^N 1,1 ^{+ N} 2,2 ^{+ N} 9,9 ^{+ N} 12,12 ) ^X a ^{+ N} 9,9 ^X b ^{+ N} 12,12 ^{- X} d ’

— Lg 3 — Lg 4 ⁺ Lg 9 ⁺ Lg 10 =

, = ф-a ^{+ (} N 3,3 ⁺ N 4,4 ⁺ N 9,9 ⁺ ^р^-, ⁺ N 10,10 ^X c ’

• ^L g 5 ^{+ L} g 6 ^{+ L} g 10 ^{+ L} g 11 =

= ^L 0,I0 ^X b ^{+ ( N} 5,5 ^{+ N}6,6 ^{+ N} 10,10 ^{+ N} 11,11^{) X} c ^{+ N} 11,11 ^X d ’

• ^- Lg 7 ^- Lg 8 ^{+ L} g„ ⁺ Lg 12 =

= L 12,12 ^X a ⁺ L 11,11 ^X c ^{+ ( N} 7,7 ^{+ N} 8,8 ^{+ N} 11,11 ^{+ N} 12,12^{) X} d "

В зависимости от условия задачи после решения системы уравнений необходимо воспользоваться формулами для расчета удельной эффективности и эффективности работы информационной сети в целом.

Предлагается использовать тензорный анализ для исследования эффективности работы структуры информационной структуры управления, бизнес компании (или коммерческой фирмы). На конкретном примере показано, каким образом можно определить эффективность управления. Достоинствоми подхода анализа на основе тензорной методологии является следующее:

• 1)    простота вычислений и возможность исследования сложных топологий с большим числом узлов сети (что не позволяют сделать известные методы)’

• 2)    синтез топологии структуры информационной сети управления по заранее заданным характеристикам эффективности, с целью получения оптимальной структуры.