Тензорный метод анализа эффективности информационных систем управления бизнес-компаний телекоммуникационной отрасли узловой топологии
Автор: Петров Михаил Николаевич, Треногий Николай Геннадьевич
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 1 (18), 2008 года.
Бесплатный доступ
Рассмотрено применение тензорного метода анализа эффективности систем управления бизнес-компаний телекоммуникационной отрасли узловой топологии.
Короткий адрес: https://sciup.org/148175668
IDR: 148175668 | УДК: 65.
Текст научной статьи Тензорный метод анализа эффективности информационных систем управления бизнес-компаний телекоммуникационной отрасли узловой топологии
Рассмотрим применение узлового метода тензорного анализа и вывода уравнения для анализа эффективности информационной сети управления организацией узловой структуры, состоящей из восьми ветвей.
Исходная структура управления имеет вид узловой сети систем массового обслуживания (рис. 1). Такое представление для анализа управления в коммерческой деятельности различной сложности было предложено Г. П. Фоминым [1]. Дальнейшие решения будут основываться на результатах работ [2; 3]. Основные положения использования тензорного анализа систем и сетей массового обслуживания представлены в работах [4; 5; 6].
Рис. 1.Исходнаяузловая топология
Для того чтобы не загромождать рис. 1, возле каждой ветви приведен лишь ее номер, который подставляется в индексы i соответствующих величин Lg i , N i и X i .
Параметры исходной структуры:
-
- n = 8 - число ветвей;
-
- U = 9 - число узлов;
-
- K = 1 - число подсетей;
-
- ( n - k ) = U - K = 9 - 1 = 8 - число узловых пар;
-
- k = n - ( n - k ) = 8 - 8 = 0 - число контуров.
Так как число контуров равно нулю, то исходная структура является чисто узловой.
В качестве вспомогательной будет использоваться структура примитивной узловой топологии из восьми ветвей (рис. 2).
/1 72 /8
О—>х1
Kgi\___)
[2 z] X1
X 8
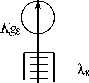
Установим геометрические объекты и уравнения состояния. Геометрические объекты, необходимые для описания примитивной структуры (в соответствии с постулатом первого обобщения), будут следующие:
-
- X - вектор, компоненты которого представляют собой удельную эффективность управлений, поступающих в соответствующие ветви;
-
- Lg - вектор, компоненты которого представляют собой эффективность управлений всей организацией, возникающих в соответствующих ветвях под действием поступающего потока удельных значений эффективности;
- N - квадратная матрица размерностью и строк на и столбцов. Элементы главной диагонали представляют собой значения удельных эффективностей на выходе из системы массового обслуживания, соответствующей данной ветви. Остальные элементы матрицы отражают взаимное косвенное влияние систем массового обслуживания друг на друга (использование общих ресурсов и т. д.). В данном примере косвенное влияние между системами массового обслуживания отсутствует, поэтому все недиагональные элементы матрицы У равны нулю:
|
N .,1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
N 2,2 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
N 3,3 |
0 |
0 |
0 |
0 |
0 |
|
|
N = |
0 |
0 |
0 |
N 4,4 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
N 5,5 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 N 6,6 |
0 |
0 |
||
|
0 |
0 |
0 |
0 |
0 |
0 |
N 7,7 |
0 |
|
|
0 |
0 |
0 Lg = |
0 ⎡⎢ Lg 1 ⎤ ⎢ ⎢ Lg 2 ⎢⎢ Lg 3 ⎢ Lg 4 ⎢⎢ Lg 5 ⎢ Lg 6 ⎢ ⎢ Lg 7 ⎢⎣ Lg 8 ⎦ |
0 ⎡λ 1 ⎤ ⎥ ⎢ ⎢λ 2 ⎥⎥ ⎢⎢λ 3 , X=X 4 ⎥ ⎢λ 5 X 6 ⎥ ⎢λ 7 ⎥ ⎣ λ 8 ⎦ |
0 ■ |
0 |
N 8, |
|
Матричное уравнение состояния примитивной структуры
X =N - Lg. (1)
Так как матрица N- диагональная, то эквивалентная система уравнений состояния примитивной структуры может быть получена перемножением соответствующих компонент матрицы N и вектора Lg:
Рис. 2. Структура примитивной узловой топологии
X 1 -Nm ' Lg 1 ,
Математика, механика, информатика
X2 - ^2d' Lg 2’
X 3-Nf33 - Lg3,
X 4 = ^ 4,4 ' Lg 4 ’
X 5 =^ 5-5 ' Lg 5 ’
X 6 = ^ 6,6 ' Lg 6 ’
X 7= ^ 7,7 ‘ Lg 7 ’
^ 8=4,8 ' Lg 8 -
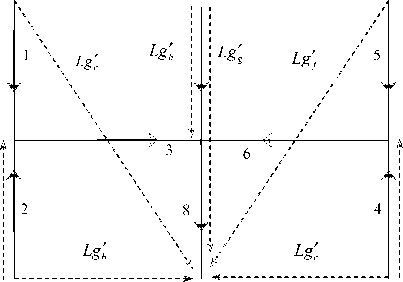
Определим тензор преобразования. Направления совокупных коэффициентов готовности в выбранных узловых парах (открытых путях) будут следующими (рис. 3).
Тогда выражения эффективности управления в ветвях примитивной структуры через совокупные эффективности в открытых путях исходной структуры и матрица преобразования будут
Lg 1 = Lga — Lg b + Lg c ,
Lg 2 = Lg a -
Lg 3 =- Lga + Lgb - Lgg + Lgh ,
Lg 4 = Lg d -
Lg 5 = Lg d — Lg. + Lg f -
Lg 6 =- Lgd + Lge - Lgg + Lgh ,
Lg 7 = Lg h -
Lg 8 = Lg g - Lg h -
A =
|
а |
ь |
с |
d |
е |
1 /1 А |
h |
|
|
1 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
-1 |
1 |
0 |
0 |
0 |
0 |
-1 |
1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
-1 |
1 |
0 |
0 |
|
0 |
0 |
0 |
-1 |
1 |
0 |
-1 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-1 |
а транспонированная матрица преобразования -
Lg a ′
A
T
|
1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
|
-1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
-1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
-1 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
-1 |
0 |
0 |
-1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
-1 |
Найдем геометрические объекты, соответствующие исходной системе.
Эффективность управления в открытых путях исходной системы (между двумя узлами узловой пары) определим по формуле:
Рис. 3. Открытые пути в исходной структуре
|
1 -1 |
1 0 |
-1 1 |
0 0 |
0 0 |
0 0 |
0 0 |
0 0 |
X 1 X 2 |
X 1 + X 2 -X 3 -X 1 + X 3 |
|||
|
X = A T • X = |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
X 3 |
X 1 |
||
|
0 |
0 |
0 |
1 |
1 |
-1 |
0 |
0 |
X 4 |
= |
X 4 + X 5 -X 6 |
||
|
0 |
0 |
0 |
0 |
-1 |
1 |
0 |
0 |
X 5 |
-X 5 + X 6 |
|||
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
X 6 |
X 5 |
|||
|
0 |
0 |
-1 |
0 |
0 |
-1 |
0 |
1 |
X 7 |
-X 3 -X 6 + X 8 |
|||
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
-1 |
X 8 |
λ 5 +λ 6 +λ 7 -λ 8 |
Значения эффективности управления в открытых путях (между узлами узловых пар) исходной системы получим по следующей формуле:
N ‘= A T • N • A. (2)
Для экономии места применим следующее правило: при умножении любой матрицы М на диагональную
(если такое умножение возможно) эта матрица сохраняет свою размерность, а каждый ее ненулевой элемент M , , j умножается на диагональный элемент N j , j в соответствующем столбце. Таким образом, после проведения первого умножения получим:
N ′ = AT ⋅ N ⋅ A =
|
N 1,1 |
N 2,2 |
- N 3,3 |
0 |
0 |
0 |
0 |
0 |
1 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
- N 1,1 |
0 |
N 3,3 |
N 4,4 |
N 5,5 |
- N 6,6 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
N 1,1 |
0 |
0 |
0 |
— N 5,5 |
N 6,6 |
0 |
0 |
-1 |
1 |
0 |
0 |
0 |
0 |
-1 |
1 |
|
|
0 |
0 |
0 |
0 |
N 5,5 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-1 |
1 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
0 |
-1 |
1 |
|
|
0 |
0 |
- N 3,3 |
0 |
0 |
- N 6,6 |
0 |
N 8,8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
0 |
0 |
N 3,3 |
0 |
0 |
N 6,6 |
N 7,7 |
— N 8,8 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-1 |
|
N 1,1 + N 2,2 + N 3,3 |
- N 1,1 - N 3,3 |
N 1,1 |
0 |
0 |
0 |
N 3,3 |
— N 3 3 |
|
- N 1,1 - N 3,3 |
N 1,1 + N 3,3 |
- N 1,1 |
0 |
0 |
0 |
- N 3,3 |
N 3,3 |
|
N 1,1 |
- N 1,1 |
N 1,1 |
0 N 4,4 + N 5,5 + + N 6,6 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
- N 5,5 - N 6,6 |
N 5,5 |
N 6,6 |
— N 6,6 |
|
|
0 |
0 |
0 |
- N 5,5 - N 6,6 |
N 5,5 + N 6,6 |
- N 5,5 |
- N 6,6 |
N 6,6 |
|
0 |
0 |
0 |
N 5,5 |
- N 5,5 |
N 5,5 |
0 |
0 |
|
N 3,3 |
- N 3,3 |
0 |
N 6,6 |
- N 6,6 |
0 |
N 3,3 + N 6,6 + N 8,8 |
_M _M _ N 3,3 N 6,6 — N 8,8 N 3,3 + N 6,6 + |
|
- N 3,3 |
N 3,3 |
0 |
- N 6,6 |
N 6,6 |
0 |
- N 3,3 - N 6,6 - N 8,8 |
|
|
+ N + N 1,1 0,0 |
В заключение найдем уравнение состояния исходной структуры. Согласно постулату второго обобщения [2], уравнение состояния исходной структуры, записанное в матричной форме, имеет тот же вид, что и уравнение состояния примитивной структуры:
X‘ = N '• Lg’ . (3)
Эквивалентная система уравнений состояния исходной структуры будет
-
X 1 + Х 2 - Х з = ( N 1,1 + N 2,2 + N 3,3 ) Lg + +(- N 1,1 - N 3,3 ) Lg b + ( N 1,1 ) Lg' c +( N 3,3 ) Lg g + (— N 3,3 ) Lg ‘ , -с+Х 3 =(— N I,, — N 3,3 ) Lg a + +( N 1,1 + N 3,3 ) Lg b + (— N 1,1 ) Lg' c + +(— N 3,3 ) Lg + ( N 3,3 ) Lg' h ,
X 1 = ( N 1,1 ) Kg a + (— N 1,1 ) Lg b + ( N 1,1 ) Lg' c , X 4 + X 5 -X 6 = ( N 4,4 + N 5,5 + N 6,6 ) Lg d + +(— N 5,5 - N 6,6 ) Lg' « + ( N 5,5 ) Lg f + +( N 6,6 ) Lg g + (— N 6,6 ) Lg h -X 5 +X 6 = (— N 5,5 - N 6,6 ) Lg d +
-
• +( N 5,5 + N 6,6 ) Lg b + (- N 5,5 ) Lg f + +(- N 6,6 ) Lg g +( N 6,6 ) Lg h , X 5 = ( N 5,5 ) Lg d + (— N 5,5 ) Lg e + +( N 5,5 ) Lg f ,
-
-X 3 -X 6 + X 8 = ( N 3,3 ) Lg a +
+(— N 3,3 ) Lg b + ( N 6,6 ) Lg d + (— N 6,6 ) Lg ‘ +
+( N 3,3 + N 6,6 + N 5,8 ) Lg g + +(— N 3,3 - N 6,6 - N 8,8 ) Lg b , X 5 + X 6 + X 7 — X 8 = (— N 3,3 ) Lg a + +( N 3,3 ) Lgb + (— N 6,6 ) Lg d + ( N 6,6 ) Lg= + +(- N 3,3 - N 6,6 - N 8,8 ) Lg g +
+( N 3,3 + N 6,6 + N 7,7 + N 8,8 ) Lg'h ■
В зависимости от условия задачи после решения системы уравнений необходимо воспользоваться формулами для расчета удельных эффективностей и суммарной эффективности в ветвях исходной структуры.


