Тензорный метод Крона, LT метод Бартини - Кузнецова, двойственные сети и диалектические противоречия

Пространство и время

Сначала было пространство , и было оно пустое и безвидное . Просто пустота. Затем в пространстве появились точки, линии, поверхности, объемы и другие объекты геометрии. Они уже имеют форму, но не имеют материального содержания. И составили они разные и причудливые комбинации структуры, заполнив пространство. Одни геометрические объекты можно выражать через комбинации других геометрических объектов. Так возникают числа, системы координат и базисы. Замкнутые и разомкнутые пути пролегают через точки и линии, а также плоскости и объемы, связывая структуры. Существуют пути, состоящие из линий, плоскостей, объемов, и т.д. Базисы этих путей преобразуются друг в друга с помощью матриц преобразования.

Замкнутые и разомкнутые пути обладают фундаментальными свойствами, которые присущи окружающему нас миру, независимо от наличия или отсутствия материи. Например, свойство асимметрии : разомкнутые, открытые пути нельзя выразить через замкнутые пути (контуры), а замкнутые пути можно выразить через открытые пути. Пространство обладает свойством двойственности структуры , когда замыканию пути в одном подпространстве, соответствует размыкание пути в двойственном подпространстве, и наоборот. Только вместе двойственные подпространства составляют полное пространство, сохраняющее постоянство открытых и замкнутых путей. Но пространство пока еще пустое. В нем нет времени.

От ред. совета Б.Б.Е.: Здесь следует обратить внимание, что понятие «пустое пространство» имеет принципиально отличную трактовку в разных Научных школах математики.

В современной теоретико-множественной школе группы Н.Бурбаки пустое пространство (множество) содержит элементы не тождественные самим себе, то есть изменяющиеся во времени. Здесь пустое пространство содержит время и по этой причине изменяется. Очень похоже, что в этом случае «пустое пространство» является реальным (физическим), а не математическим пространством.

В другой, - математической школе Клейна, Веблена, Арнольда – понятие «пространство» связано с различными видами геометрий и их инвариантами с определенными группами преобразований. Здесь действительно отсутствует величина «время». Но здесь отсутствует и пустое пространство в том смысле, как это понимает автор.

Оригинальность позиции автора состоит в том, что у него пустое пространство не содержит не только время, но и геометрические объекты. Здесь нет точек, линий, поверхностей, объемов и т.д. Нет и времени.

Очевидно, что здесь автор выходит за классические рамки не только доминирующей математики, но и физики. Он хочет получить «всё» из «ничего». Его «ничего» – это пустота. Его «всё» – это материальный мир, описываемый языком математики и физики, где отсутствует понятие «пустота» в понимании автора.

По-видимому, автор хочет предложить возможный вариант новых «начал», опираясь при этом на тензорный метод Г.Крона и LT-метод Бартини – Кузнецова.

При этом, уважая время читателя, он не стал объяснять, что в пустом пространстве не все так просто.

Как из «ничего» получить точку, отрезок, объем и т.д.? Может быть, развиваемая автором методология двойственных пространств поможет ответить на этот вопрос.

Не сразу бросается в глаза, что неопределенность понятия «пустота» связана не с нулем (который в пустоте еще не родился как число), а с вечностью и бесконечностью в их соотношении. Не случайно именно эта пара понятий является началом Ведической пранауки. Прошло не одно тысячелетие, прежде чем континуум – гипотеза в терминах актуальной бесконечности Кантора была фактически признана недоказуемой (А.Зенкин Вопросы философии, вып. №2, 2000. – с. 165 – 168). Но еще в 1911 году голландский математик Л.Брауэр привел фундаментальное доказательство, согласно которому одномерные объекты (отрезки) не могут непрерывно переходить в нульмерные (точки) и, наоборот. Более того, возникновение нового геометрического объекта с иной LRT0-размерностью – это всегда прерывание непрерывности, эти всегда переход в новую систему координат, новое качество.

По этой причине пересчет действительных чисел внутри данного качества, определяемого целочисленной LR-размерностью геометрического объекта, потенциально бесконечен. Сколько существует новых качеств (объектов) – столько и бесконечностей. Если новых геометрических объектов бесконечно много, то имеет место бесконечность бесконечностей.

Более того, в реальном (физическом) мире новое качество (новый геометрический объект) всегда рождается во времени. Преобразование объектов представляет процесс, который не может существовать вне времени. Рождение нового объекта (точки) из «ничего» также является процессом. И поскольку количество точек потенциально бесконечно, процесс потенциально вечен. Отсюда следует, что пустота есть вечный без телесный поток (процесс).

Всё телесное (пространственное) происходит из без телесного (временнóго). Это положение является фундаментальным в началах Г.Лейбница – его монадологии, где первоначалом мироздания является духовная монада, которую ученик Г.Лейбница Я.Герман связал со свойствами без телесного мира вечного потока времени [L0T0].

Подробнее о началах Лейбница и взаимосвязи с физической монадой М.В.Ломоносова можно прочитать в работе Б.Е.Большакова, О.Л.Кузнецова [2].

Затем появляется материя . Как? В результате вмешательства, типа большого взрыва, или изначально была, но не проявляла себя, или иным образом. Материя характеризуется массой, веществом и энергией; они взаимно превращаются друг в друга. Пространство само вроде бы не обладало этими свойствами. И вот когда линии и плоскости с объемами наполняются материей (точки образуют границы), а через материю распространяются потоки энергии, то в пространстве возникают процессы. Разные виды материи создают процессы распространения механической, тепловой, электромагнитной, ядерной, гравитационной энергии. Процессы предстают как воздействия источников энергии на материю, в которой возникают отклики, и эти процессы в многообразии своем распространяются в пустом и до этого мертвом пространстве, заполняя его светом энергии и наполняя жизнью. Эти процессы происходят в пространстве, которое изначально обладает свойством двойственности.

Движение требует возникновения времени . Это свойство природы, которое позволяет отличить положение одного и того же (точки, тела, системы) в разных местах пространства. Пока нет времени – точки, плоскости, пути прикреплены к своему положению в пространстве, и неподвижны. Материальные и нематериальные объекты могут находиться везде, в разных местах, ибо нет меры, которая отличает их положение. Время дает меру перемещения вещей в пространстве. Связь пространства и времени создает движение.

Перемещения в пространстве возможны поступательные (прямолинейные) и вращательные, или их комбинация. Здесь проявляется фундаментальное отличие замкнутых и открытых путей. Поступательное движение по открытому пути так удаляет предмет от наблюдателя, что он становится ненаблюдаемым. По этой причине время измеряется с помощью вращательного движения, когда замкнутый путь возвращает предмет наблюдения в исходную точку через определенные промежутки времени.

В одном месте пространства, в одно время может находиться одно тело, другие тела сюда поместить нельзя. Это фундаментальное свойство выражает принцип Паули (принцип запрета) — один из фундаментальных принципов квантовой механики, согласно которому два и более тождественных фермиона не могут одновременно находиться в одном квантовом состоянии. Принцип, который Вольфганг Паули сформулировал для электронов в 1925 году, и обобщил в 1940 году, утверждает, что в пределах одной квантовой системы в данном квантовом состоянии может находиться только одна частица, состояние другой должно отличаться хотя бы одним квантовым числом.

Следствием принципа является постепенное заполнение электронных оболочек в структуре атома. Само существование оболочек является структурным свойством пространства, из которого следует разнообразие химических элементов и их соединений. Принцип Паули запрещает электронам принимать одинаковые квантовые состояния. По этой причине электроны не могут быть в одном квантовом состоянии с наименьшей энергией, а заполняют последовательно квантовые состояния оболочки, с наименьшей (свободной в данный момент) суммарной энергией. Примером является атом лития (Li), у которого два электрона находятся на 1S орбитали (самой низкой по энергии), при этом у них отличаются собственные моменты импульса, и третий электрон не может занимать эту орбиталь. Третий электрон занимает 2S орбиталь (следующая, низшая по энергии, орбиталь после 1S).

Это свойство заполнения свободного места, и запрета заполнять занятое место, действует и для людей. Известно, что из двух близнецов, во всем одинаковых, один обладает характером лидера (альфа), а другой – ведомого (омега). По этой причине, как и в атоме, в обществе начинают заполняться наиболее низкие уровни по интеллектуальному развитию. Когда они заполнены, возникают личности с более высоким интеллектом, а по мере их заполнения возникают личности с все более высоким творческим потенциалом. Таким образом, чтобы создать гения, надо сначала создать много не гениев.

Процессы и структура

По мере заполнения в обществе низких уровней, возникли ученые, и стали описывать процессы в одной науке, а структуру связей – в другой науке. Природа не знает о том, что ученые разделили ее на отдельные науки. Процессы описывают уравнениями поведения, которые связывают воздействия на систему и свойства сопротивления ее материи с реакцией системы, т.е. откликами на приложенное воздействие. Например, в электротехнике это ток в ответ на приложенный источник напряжения, или напряжения на ветвях на приложенный источник тока. Структура описывает связи элементов системы, которые создают замкнутые и разомкнутые пути для прохождения потоков энергии. Уравнения для процессов связаны с метрическими пространствами и не содержат структуру. Структуру представляют графами, сетями, симплексами, комплексами, но они не содержат метрики.

Основным достоинством тензорного метода, который разработал Габриель Крон, стало соединение в одном подходе процессов и структуры. По сути Крон, как инженер-электрик, сделал первую попытку связать метрику и структуру, сначала на уровне инженерного расчета и проектирования цепей и электрических машин. Он задавал описание структуры через токи в контурах и пары узлов, на которых возникают напряжения. Для этого он выражал токи в контурах связанной сети через те токи, которые протекали бы в свободных ветвях (включающих в себя источники напряжения или тока).

Коэффициенты такого выражения составляют матрицу преобразования токов, которая обозначается С . В связанной сети независимых контуров меньше, чем в свободных замкнутых ветвях, каждая из которых сама образует контур. По этой причине матрица преобразования токов оказывается прямоугольной.

Тензоры – отражение измеримых величин

Тензоры возникли из необходимости описать объекты в пространстве для наблюдателя, которому это надо для того, чтобы сообщить другим наблюдателям. Таким образом, тензоры – это средство создания языка общения наблюдателей. Существует проблема реальности и ее отражения человеком для анализа, исследования и, в конечном счете, развития жизни. Для этого вводят системы отсчета, координат, в которых числа отражают математическую «тень» реальности. При изменении координат меняются числа (компоненты, проекции), но не сама реальность. Хотя сама независимость объекта наблюдения от наблюдателя является одной из проблем измерений.

В математике ввели цилиндрические, сферические, криволинейные системы координат, в которых один объект имеет разные компоненты. Независимые контуры и пары узлов (открытые пути) представляют электрические процессы в цепях. Вращающиеся системы координат связаны с ротором электрической машины. В экономике реальные потоки продуктов и денежных средств отражают в разных системах отчетности (планы счетов, вводимые международные стандарты финансовой отчетности, МСФО и т.д.). Понятию реального, измеримого объекта в математике, по сути, соответствует понятие тензора.

Начиная с середины XIX века, тензоры стали использовать в механике при описании упругих деформаций. Первоначально тензорный анализ называли «абсолютное исчисление». Как составная часть дифференциальной геометрии тензорное исчисление было рассмотрено Г.Риччи и Т.Леви-Чивита. Термин «тензор» ввел В.Фойгт в 1898 году, хотя некоторые считают, что это сделал А.Эйнштейн в 1916 году. Г.Крон первым применил тензоры для расчета электрических машин, а затем в электротехнике.

Суть тензорного метода состоит в признании инвариантности объекта в пространстве (вектора, многомерного объема в геометрии; измеримой величины в физике, технике или экономике). Реальный объект существует независимо от субъективных систем координат наблюдателя, в которых объект представлен компонентами (измерен). Если компоненты объекта при изменении системы координат преобразуются по линейным законам (умножением на матрицу преобразования базиса), то это является признаком измеримости объекта и такой объект называется тензором.

В качестве обобщения понятия тензора рассматривается абстрактная система для процессов и структуры одного типа, а конкретные системы рассматриваются как ее «проекции» в координаты, заданные структурой связей. Это позволяет создать обобщенные математические модели и теории в разных предметных областях.

Поток энергии как единая сущность

Но тот, кто взирает познанья глазами, поймет, что единая сущность – основа… Махабхарата

Применение тензорного метода к исследованию сложных систем началось с электрических машин, которые считались столь сложными системами, что для каждого типа создавалась своя теория (а порой и несколько). «Основателем обобщенной теории электрических машин является Г. Крон, который в 30-х годах предложил уравнения обобщенной машины. В последние десятилетия благодаря применению ЭВМ усилиями многих ученых-электромехаников обобщенная теория электрических машин получила дальнейшее развитие. …Большинство успехов в теории и практике электромашиностроения связано с математической теорией электрических машин» [4] ( Копылов , 2000, с. 41).

Обобщенная электрическая машина Крона в минимальной форме реализует процесс электромеханического преобразования потока энергии. Другие электрические машины отличаются от обобщенной машины количеством элементов, осуществляющих этот процесс, и количеством связей между ними. Переход от одной машины к другой задает матрица преобразования, которая показывает, как отличаются структуры соединения машин.

В работе «Единая теория электрических машин» [13] ( Kron , 1930) все электрические машины, которые до этого считались несопоставимыми, исследованы с единой точки зрения построения диаграмм , которые показывают величину и направление потоков энергии между различными частями сложной машины. Для этого было применено понятие свободная энергия из термодинамики.

Основы тензорной теории электрических машин представлены в статье «Нериманова динамика вращающихся электрических машин» [16] ( Kron , 1934). В 60-тых годах в трудах

Японской ассоциации прикладной геометрии данная статья охарактеризована как «сделавшая эпоху». Было введено понятие простейшей (обобщенной) электрической машины из двух элементов – обмоток. Уравнения поведения обобщенной машины Крон получил из уравнений Лагранжа. Тогда уравнения любой машины с другим числом и соединением элементов получаются умножением величин в уравнениях простейшей системы координат (обобщенной машины) на матрицу преобразования C , которая показывает, как соединены обмотки в исследуемой машине. Оказалось, что уравнения электрических машин при стационарном режиме имеют такой же вид, как для неподвижных сетей, при условии, что обычное дифференцирование в уравнении

ザ dナサ e8 = R ■ i + dt                                                   (!)

заменяется ковариантным дифференцированием, δ / dt , при котором учитывается изменение вектора при его параллельном переносе вдоль кривой в римановом пространстве:

el = ^RBEi⁸ +      ’                                                   (2)

dt где e – напряжение; R – сопротивление (резистанс);

i – ток; ϕ – магнитный поток;

t – время;

δϕ α /dt – ковариантная производная, учитывающая изменение вектора при параллельном переносе в криволинейном римановом пространстве.

При малых колебаниях около стационарного вращения – качаниях, это уравнение принимает вид:

S e a = ^R .^{5 +} L ae ⁵^ ^{+ K} .^ ^ dx ^{+ R} ae/ ^dx ' ,            ⁽³⁾

где R αβγ – тензор третьего ранга, определяемый сопротивлениями;

K δγβα – тензор кривизны Римана – Кристоффеля, наличие которого показывает, что поведение вращающейся электрической машины в режиме качания описывается как движение представляющей точки в неримановом пространстве с асимметричной связью (с кручением).

Форма уравнений для стационарного режима, ускорения и качаний остается одна и та же , но само пространство усложняется за счет все большего искривления. Искривление пространства, представляющего поведение машины, подобно искривлению физического пространства вблизи тяготеющей массы, которое отклоняет луч света (поток фотонов)

проходящий мимо поля солнечного тяготения. А.Эйнштейн считал, что Крон распространил в область техники идеи общей теории относительности. Н.Винер отметил, что Крон ввел новый язык, который позволяет не только поставить задачи расчета машин единым образом, но и дать новые методы решения таких задач [19] ( Wiener , 1936).

Постулат Крона об инварианте мощности и противоречия тензорного метода

Крон исследовал преобразования токов и напряжений при изменении соединения ветвей в цепи. Для этого он ввел понятие простейшей (из отдельных ветвей) сети. Другие сети из данных ветвей являются вариантами соединений ветвей простейшей сети [6] ( Крон , 1978). Для получения уравнений соединенной сети из уравнений простейшей сети использовались матрицы преобразования, которые связывают токи в контурах простейшей сети с токами в контурах соединенной сети (или напряжения на свободных ветвях с напряжениями в разомкнутых путях связанной сети). Они представляют матричную запись законов Кирхгофа.

Токи при изменении структуры преобразуются как контравариантные величины, а напряжения – как ковариантные величины. Впервые контравариантный характер токов и ковариантный характер напряжений заметил Г.Вейль, опубликовавший статью в 1923 г. в испано-американском математическом журнале [18] (Weyl, 1923). Автор показал, что эти физические величины преобразуются относительно изменения базиса путей, т.е. структурных величин сети, где пути играют роль координат.

Крон утверждал, что при соединении ветвей рассеиваемая мощность в электрической цепи не меняется – поскольку остаются прежними источники тока и напряжения, которые задают в сети поток энергии. Это необходимо для получения тензорных формул преобразования напряжения. Постулат об инварианте мощности позволял получить формулу преобразования напряжения. Это ключевой пункт построения тензорного анализа сетей .

Однако известно, что мощность (поток энергии) меняется при изменении связей при изменении структуры . Для заданной цепи, состоящей из резисторов и источников, величина напряжения на всех резисторах не выше суммы величин напряжений на источниках. Это следует из теоремы Волавера в теории графов о неусилении мощности в резистивной сети. Суть доказательства в том, что в ориентированном графе каждое ребро находится либо в ориентированном цикле, либо в ориентированном сечении, либо отсутствует в обоих.

Под расчетом цепи понимается вычисление электрических величин или их отношений при заданных схеме и параметрах цепи. В частности, задача состоит в определении откликов в соединенных ветвях при заданных воздействиях в отдельных ветвях. При этом должны выполняться законы Кирхгофа о равенстве нулю суммы токов в каждом узле и равенстве нулю суммы напряжений в каждом контуре.

Суть тензорного метода Крона в электротехнике в том, что к уравнениям процесса прохождения электрического тока добавлено описание структуры связей. Для этого введены матрицы преобразования. Токи i “ и напряжения е _а на свободных ветвях связаны законом Ома: е _а = z _ар i ^р , где z _ар - матрица комплексных сопротивлений, которая при индуктивном взаимодействии ветвей может и не быть диагональной ( а , р = 1  n ). Если воздействия -источники ЭДС е _а , то откликами являются токи i “ , для которых уравнения составляют по независимым т контурам. Это система уравнений в матричном виде:

еа' = Za'P' р(4)

Для ее решения обращают матрицу комплексных сопротивлений (z_а-р-)"¹ = у “^р , тогда:

iP ' = (Za-в)"1 еа' = У"в' еа',(5)

и по токам в контурах ie' можно определить n токов в ветвях ic р = тСаа'  iр', а затем напряжений в ветвях е са = zар i с р, что является решением задачи цепи.

Если воздействия - источники тока Г “ , (Крон обозначал в этом случае величины заглавными буквами), то отклики - напряжения Е _а , для которых уравнения составляют по независимым парам узлов (базис разомкнутых путей). Система уравнений для j = n - т пар узлов (разности потенциалов отсчитывают относительно базисного узла) в матричном виде:

Г“' = У “^р Е р- .                                                  (6)

Решение этой системы также достигается обращением матрицы:

Е р- = (У “'^р )^-1 Г “ '= 2 а-р- 1“' .                                       (7)

Полученные так j напряжений в разомкнутых путях Ев' позволяют определить n напряжений в ветвях Еср, а затем и n токов в ветвях Г"'  У“р Ер, что является решением задачи цепи. Проверкой является выполнение законов Кирхгофа для найденных токов и напряжений.

Контурный метод и узловой метод расчета цепи Крон представил как преобразования тензоров в пространстве сети, где метрический тензор – сопротивление, а ток и напряжение – контравариантные и ковариантные векторы. В основе метода преобразование токов при соединении ветвей в сеть. Коэффициенты выражения токов в n свободных ветвях i “ через токи в т контурах связанной сети i “ ' составят матрицу ^тС“_а- (порядка т x n ):

i ^a = ^mC^a_a- i ” .                                                   (8)

Строки матрицы ^mC показывают, в какие контуры входит данная ветвь, а столбцы - из каких ветвей состоит контур. Рассеиваемая мощность P равна сумме мощностей на ветвях, т.е. произведений напряжения и тока в каждой свободной ветви: P = e _a i ^a .

Аналогично для напряжений и токов в контурах связанной сети:

P' = ea- г,(9)

где предполагается сумма по одинаковым верхним и нижним индексам. Если постулировать , что мощность при изменении соединений не меняется, и подставить (8), то получим закон преобразования для напряжения, e_a- i^a' = e _a i ^a = e _a C ^a _a- i^a' , откуда:

ea- = ea mCaa- = mCaa-t ea,(10)

где индекс t означает транспонирование матрицы. Чтобы получить формулу преобразования z _ae , подставим (8) и (10) в (9):

ea = Zae ie = Zae "CV i”,(11)

но для этого надо в (10) получить обратное преобразование ea = ("C”,-,)"1 ea-. Это возможно когда сеть состоит из одних контуров; в этом случае матрица Caa- квадратная, и может иметь обратную матрицу. В общем случае, когда число контуров меньше числа ветвей, это невозможно, поскольку матрица mCaa прямоугольная, для нее не существует обратной матрицы. Однако если формально подставить в (11), то:

ea = («"„t)" ea- = Zae mC-: ‘ ”',(12)

а затем умножить обе части уравнения на матрицу ( " C ^a _a-)_t то получим:

(mC”a;)t (mC-a-,)"1 ea- = <(«"„), Zaf "C :.)" i” = ea',(13)

откуда, используя постулат о том, что вид уравнений поведения не меняется при соединениях [6] ( Крон , 1978), получим формулу преобразования импеданса:

Z-T = fCMt Zae "C . .(14)

В этой формуле нет обратных матриц преобразования, а значит и не надо «обращать» прямоугольные матрицы. Далее расчет производится контурным методом. Если подставить все формулы преобразования в выражение токов в ветвях связанной сети, то получим:

ic в = "С” ("C"at Zae mCaa)"1 "C”,; e, = mYc ea(15)

Матрицу ^mY_c , которая выражает токи в ветвях связанной сети через заданные источники ЭДС, назовем матрицей решения .

Делая двойственные замены величин, получим формулы расчета цепи узловым методом, при этом матрица C заменяется на ортогональную матрицу А = C1,. Крон полагал, что матрица А не имеет такого структурного смысла, как матрица С. Автор показал, что матрица А является также матрицей преобразования С = А, но в двойственной цепи (сети).

Обосновать постулат об инварианте мощности пытались физики, например, Б. Гофман, и математики, Дж.Рот. Дискуссия по применению тензоров в технике растянулась на десятки лет. Эти обсуждения, в том числе на страницах журнала «Электричество», носили, как отмечал автор, острый характер, порой выходя за рамки научной терминологии [8] ( Петров , 1985). Одни применяли тензорный метод в различных областях физики и техники. Другие отвергали его за прямоугольные матрицы, которые не образуют группу. Несмотря на проблемы, «эти работы, несомненно, оказали глубокое влияние на развитие многих областей знания и способствовали прогрессу в разработке методов решения системных задач с помощью цифровых вычислительных машин» [3] ( Веников , 1985).

Аналогии предметной области и сетевой модели

Крон писал, что чем дальше он уходил от электротехники, к сетевым моделям в физике, технике, тем более точно пришлось определять основные понятия в самой электротехнике. Сегодня можно сказать, что здесь проявились общие законы структуры, которые присущи всем неживым и живым системам, от микромира до космических масштабов. Крон создал целый ряд сетевых моделей в виде электрических цепей. Цепи были его языком моделирования, матрицы преобразования Крона выражают токи в связанной цепи, через токи в свободных ветвях. Позднее он признавал, что замкнутые и разомкнутые пути в сети – это более абстрактные средства для представления потоков энергии, чем физические величины тока и напряжения.

От ред. совета Б.Б.Е.: Если принять во внимание близость понятий «замкнутые и разомкнутые пути в сети» с понятием «замкнутая и открытая система», то для описания потоков энергии эти понятия дают более глубокое представление, чем электрические величины тока и напряжения.

Как показано в работе [1] поток энергии может быть выражен не только через ток и напряжение, А поскольку количество физических величин потенциально бесконечно, то и описаний потока энергии потенциально бесконечно при одном условии, что показаны условия, при которых величина удовлетворяет требованиям открытых и замкнутых систем.

Крон моделировал эквивалентными цепями технические, физические системы, которые имели аналогии процессов и структуры. Были построены модели в виде эквивалентных электрических цепей для уравнений поля Максвелла (Kron, 1944), Шредингера (Kron, 1945), Навье-Стокса, модели упругих систем (строительные конструкции, разрезные диафрагмы турбин), модели электронных ламп, многоатомных молекул, электрических машин, сетей передачи электроэнергии, ядерного реактора, транспортной задачи и другие. Эти модели представлены в Диакоптике [5] (Крон, 1972), как основа алгоритмов для расчета сложных систем по частям.

До появления ЭВМ Крон в 40-е годы применял физические реализации моделей как аналоговые машины для решения задач, например, распространения электромагнитных волн в полых резонаторах ( Carter, Kron , 1944, 1945). С появлением цифровых ЭВМ матричное представление задач и структуры систем применялось для расчета эквивалентных моделей предметных областей [5] ( Крон , 1972). С развитием ЭВМ с параллельной архитектурой расчет сетей по частям стал одним из методов организации (на уровне математической модели) параллельных вычислений ( Петров , 1991), в том числе для транспьютеров ( Bowden K ., 1988, 1989). Расчет больших систем на сети транспьютеров с помощью диакоптики в параллельной форме рассматривали Фуско и Меругу ( Fusco V. F., Merugu L.N., 1991).

В перспективе представляют интерес работы Крона по многомерным (полиэдральным) сетям. Полиэдральные сети, рассмотренные в статьях 1958–1968 гг., состоят не только из одномерных ветвей, но также из плоскостей, точек, объемов, многомерных элементов; и проводят не только электрический ток, но и потоки энергии других видов. Например, магнитные и диэлектрические силовые линии определяются через поверхностные интегралы по некоторым плоскостям графа, ограниченным контурами. Магнитный поток распространяется через двумерные поверхности (представлены обмотками в электрической машине). Таким образом, электромеханические преобразователи (электрические машины) являются простейшим примером полиэдральных сетей, в данном случае двумерных сетей.

Совокупность сетей из точек, отрезков, плоскостей и т.д., или 0-, 1-, 2- и т.д. – до n-мерных симплексов, при возбуждении электромагнитными волнами Крон назвал волновым автоматом. Он применял такой волновой автомат в качестве многомерного пространственного фильтра, для проведения многомерных кривых по экспериментальным данным методом наименьших квадратов в регрессионном анализе [15] ( Kron , 1962). Двойственными к p -сетям рассматриваются (n – p) -сети в n -мерном пространстве [14] ( Kron , 1965). Крон утверждал, что полиэдральные волновые автоматы обладают свойствами самоорганизации в смысле изменения параметров их состояния в ответ на внешние воздействия. Воспроизвести режим самоорганизации полиэдральной сети последователям Крона в дальнейшем не удалось, хотя в Англии Дж.Линн повторил расчеты Крона с помощью волнового автомата [18] ( Lynn , 1974).

LT метод Бартини-Кузнецова

Важнейшим элементом моделирования являются аналогии между предметной областью и сетевой моделью. Аналогии между структурой путей, связанных элементов распространения потоков энергии достаточно наглядны и понятны. Сложнее понять аналогии между воздействиями и откликами механической, гидравлической, тепловой, электромагнитной, экономической системы и величинами сети. Что же позволяет их сопоставить и сравнить? В чем аналогии измерения столь различных измеримых величин?

Существует немало систем измерения физических величин, которые выбирают тот или иной набор величин в качестве базисной основы. Остальные физические величины определяются через базисные величины. Это позволяет сопоставлять физические величины, которые относятся к разным предметным областям, с помощью анализа размерностей. Понятие размерности ввел в физику Фурье в 1822 году.

От ред. совета Б.Б.Е.: Следует ввести уточнение. Впервые понятие «размерность» как физикоматематическая категория встречается в форономии Я.Германа в 1716 году для установления связи телесных (геометрических) и без телесных (хронометрических) величин. Фурье в 1822 году ввел понятие размерность в физику для выделения границ однородных групп (качеств), а в 1855 году Дж.Максвелл ввел квадратные скобки, подчеркивая качественную определенность величин, определяемую их размерностью и единицей. Величина без квадратных скобок выражает количественную определенность, численное значение величины, определяемое её отношением к единице измерения (И.Ньютон, 1711 г.).

Принятым на сегодня в большинстве стран стандартом является международная система единиц измерения СИ. Она определяет семь основных и производные единицы физических величин: килограмм, метр, секунда, ампер, кельвин, моль и кандела. В рамках СИ считается, что эти единицы имеют независимую размерность, т. е. ни одна из основных единиц не может быть получена из других.

Вместе с тем классики утверждают, что в мире нет ничего, кроме материи, которая движется в пространстве и времени. Следовательно, можно ожидать, что существует такая система измерения, в которой все физические величины выражаются через две наиболее фундаментальные – пространство (протяженность) и время (длительность).

Возможность выразить все физические величины через длину и время отмечал Максвелл (Максвелл, 1954), а затем Кельвин, Эддингтон и другие. Разработал такую систему Б.Браун (Brown, 1941) и независимо от него в 1966 году Р.Л.Бартини (Бартини, 1965, Бартини, 1966). Система представлена таблицей, в клетках которой расположены физические величины соответствующей размерности по длине и времени. Фрагмент таблицы LT для размерностей физических величин (Бартини, Кузнецов, 1974; Большаков, 2002) представлен ниже (табл. 1). Вместе с тем П.Г.Кузнецов показал, что клетки физических величин соответствуют определенным типам геометрии, и различным видам физической теории. Каждой физической величине соответствует своя геометрия, своя группа преобразования координат соответствующей структуры.

Таблица 1. LT-таблица размерностей физических величин Бартини-Кузнецова

Время, T-1 (сек.)-1

T-5

T-4

T-3

T-2

T-1

T0

T1

T2

T3

					L3 T-6	L4 T-6	Изменение мощности	Скорость передачи мощности
			L1 T-5	Изменение давления L2 T-5	Поверхностная мощностьL3 T-5	Скорость изменения силы L4 T-5	Мощность L5 T-5	Скорость передачи энергии
			Изменение плотности тока L1 T-4	Давление L2 T-4	Поверхн. натяжение L3 T-4	Сила L4 T-4	Момент силы Энергия L5 T-4	Скорость передачи действия
	Гидравлич. сопротивле ние L-1 T-3	Изменение углового ускорения T-3	Скорость массы Плотность тока L1T-3	Напряжен. электро-магн. поля Вязкость L2 T-3	Ток Массовый расход L3 T-3	Скорость смещения заряда Импульс L4 T-3	Момент импульса Действие L5T-3	Момент действия
	Изменение объемной плотности	Массовая плотность Угловое ускорение T-2	Линейное ускорение L1T-2	Напряжение (разность потенциалов) L2 T-2	Масса , Колич-во магнетизма Заряд L3 T-2	Магнитный момент L4 T- 2	Момент инерции L5 T-2
	L-1 T-1	Частота T-1	Скорость Электрич. сопротивл. L1 T-1	Скорость изменения площади L2T-1	Скорость изменения объема L3T-1	Скорость смещения объема L4 T-1	L5 T-1
	Изменение проводимо сти	Безразмерные константы	Длина Емкость Самоиндукция L	Площадь L2	Объем L3	4-Объем L4	5-Объем L5
Изменение магнитной проницаемости	Электрич. проводимость L-1 T1	Период	Длительность расстояния	L2T1
Магнитная проницаемость	L-1 T2	Поверхность времени	L 1 T2
L -2 T 3 Текучесть	L-1 T3	Объем времени	Гидравлич. проводим. L 1 T3

L-2           L-1           L0           L1            L2            L3             L4            L5          L6

Длина L, м

Выражение величин в данной таблице через длину и время неявно предполагает тождество гравитационной и инерционной массы. «В принципе ниоткуда не следует, что масса, создающая поле тяготения, определяет и инерцию того же тела. Однако опыт показал, что инертная и гравитационная массы пропорциональны друг другу (а при обычном выборе единиц измерения численно равны). Этот фундаментальный закон природы называется принципом эквивалентности. Экспериментально принцип эквивалентности установлен с очень большой точностью» [12] (ФЭС, с 393). Существование самой LT таблицы можно считать важным теоретическим аргументом в пользу принципа эквивалентности.

От ред. совета Б.Б.Е.: Известно, что соотношение гравитационной постоянной инертного тяготения точно равно 4π, что дает возможность осуществлять переход из LT-системы в CGS [1].

Принцип эквивалентности позволяет приравнять силу в уравнениях закона гравитации F = т²/Г и второго закона Ньютона F = m а. Тогда m = Г а. Обозначая длину L , а время T , и учитывая, что размерность обозначают квадратными скобками, получим, что [ r² ] = L² , а размерность ускорения [ a ] = L 1 T² . Отсюда размерность массы получим: [ m ] = L 3 К² , т.е. она выражена через длину и время. Аналогично можно выразить электрический заряд и количество магнетизма, которые попадают в ту же клетку таблицы, что и масса. Например, количество движения (импульс), величина векторная, т.е. имеющая направление, имеет размерность в терминах пространства и времени как произведение массы и скорости:

[ p ] = [ m ] [ v ] = L 3 T"² L 1 ^1 = L⁴ T" 3 •                       (16)

Клетки таблицы физических величин на рисунке содержат величины с одинаковой физической размерностью, выраженной через пространство (длину) L и время T . Каждую такую величину следует рассматривать как инвариант, постоянство которого относительно определенной группы преобразований соответствует физической теории или закону. Как известно, различные виды геометрии отличаются инвариантами и сохраняющими их группами преобразований . Например, группе преобразований, сохраняющих длину, соответствует физика движения твердого тела. Группе преобразований, сохраняющих объем, соответствует физика движения несжимаемой жидкости, и т.д.

Уравнение инварианта потока энергии . В каждой предметной области произведение соответствующих пар продольных и поперечных величин имеет физическую размерность мощности (потока энергии). В терминах таблицы Бартини-Кузнецова это [ L5 Т5 ]. Например, электрические ток и напряжение; в механике сила в точке и скорость (как разность положения тела в двух точках в единицу времени); в гидродинамике поток жидкости (объем в единицу времени) и давление; в термодинамике поток тепла и температура; поток массы и концентрация (химический потенциал) и т.д. Распределение размерностей в каждой паре различное, но произведение величин имеет размерность [ L5 Т5 ]. Например, ток имеет размерность [ L³ К³ ], а напряжение - [ L² К² ]; давление - [ L² T ⁴ ], а поток жидкости (скорость изменения объема) - [ L³ Т1 ]; сила - [ L⁴ T ⁴ ], а скорость - [ L 1 Т1 ] и т.д. Образно говоря, если мир сложен из одинаковых кирпичей потока энергии , то в разных предметных областях эти кирпичи состоят из разных блоков. Это обстоятельство и дает основу для установления аналогий между величинами процессов при создании сетевых моделей предметных областей с помощью LT метода Бартини-Кузнецова.

В самой таблице есть скрытая и не изученная структура, которая различает физические величины по их роли в качестве воздействий и откликов (характеристик потока энергии), и характеристик материи , через которую распространяется поток энергии. Например, ток и напряжение определяют поток энергии в цепи, измеряемый их произведением, мощностью, а сопротивление или проводимость определяют электрические свойства инерции материи. Таким образом, клетки таблицы в физике предметных областей играют разную роль.

От ред. совета Б.Б.Е.: Каждая клетка в LT-системе (таблице) - это класс систем (качество), границы которого определяются LT-размерностью величины как качественно-количественной определенности. Переход из одной клетки в другую - это переход в другой класс систем, переход в другое качество с другой LT-размерностью. Подробнее можно прочитать в работах [1, 2, 7].

Воздействия и отклики. Потоки энергии предстают наблюдателю для измерения как сочетание двух величин – воздействия и отклика. Воздействие является причиной, которая прикладывается к материи, веществу, чтобы вызвать изменение, движение.

Отклик является следствием реакции материи на приложенное воздействие. Материя оказывает сопротивление изменениям, т.е. возникновению и поддержанию движения, в меру своей инертности. Такая инерционность, различная для разных видов энергии, характеризует материальные свойства материи, определяет метрику (пространства, системы).

Отклик является следствием взаимодействия причины, т.е. воздействия, и материи вещества (обладающей свойствами инерционности, косности, как говорил В.И. Вернадский). Косная материя всегда оказывает сопротивление распространению потока энергии.

Описание потока энергии как отклика материи на воздействие имеет вид: воздействие = сопротивление * отклик.

Такой вид имеют все уравнения описания процессов в элементах. Для многих элементов получаем систему уравнений. Решением является получение обратного соотношения. Воздействие и сопротивление можно измерить, а отклик надо рассчитать, т.е.: отклик = воздействие / сопротивление.

В случае многих взаимодействующих элементов воздействие и отклик представляют векторы, а сопротивление – матрица, которую надо обратить, тогда решение принимает вид: отклик = (сопротивление) ^-1 * воздействие.

Величина потока энергии измеряется как произведение воздействия и отклика. Эту величину называют мощность и определяют в зависимости от ситуации, как энергия, потребляемая в единицу времени, или энергия, производимая в единицу времени, или энергия, рассеиваемая в единицу времени. Это можно записать так:

(поток энергии) = мощность = воздействие * отклик.

Такое соотношение перекликается с представленной выше связью воздействия, отклика и метрики, выраженной сопротивление материи, которую можно записать так:

(метрика) = сопротивление = воздействие / отклик.

Для полного описания процесса получаем дихотомию из произведения и частного воздействия и отклика.

От ред. совета Б.Б.Е.: Следует обратить внимание, что предложенное автором описание потока энергии как отклика материи на воздействие может быть и иным, представленным на основе закона сохранения полной мощности: [L⁵T^-5]= const.

В структурной форме этот закон выражается базовым уравнением полной мощности П.Г.Кузнецова:

N = P + G [L5T-5], где N – полная мощность на входе или воздействие [L5T-5];

P – активная (свободная) мощность на выходе или активный отклик [L5T-5];

G – пассивная мощность или пассивный отклик [L5T-5].

Отсюда:

воздействие (N) = активный отклик (Р) + пассивный отклик (G).

Однако, уравнение полной мощности может быть записано иначе:

N(воздействие) = φ-1 (сопротивление) · Р (активный отклик)

или

N (воздействие) = (1 – φ)-1·G (пассивный отклик), где φ = активный отклик(Р), [L0T0] - эффективность использования полной мощности; воздействие (N)

φ -1 ₌ воздействие ( N ) , [ L ⁰ T ⁰] - сопротивление.

отклик ( Р )

Следует обратить внимание, что здесь сопротивление (φ-1), являясь обратной величиной эффективности, имеет размерность [L0T0], а не [L-1T-1] как у автора.

Дело в том, что у автора сопротивление определено так, как принято в электротехнике:

U [L2T-2]/ I [L-3T-3] = [L-1T-1], а в нашем случае сопротивление трактуется на основании закона сохранения как величина обратная эффективности использования полной мощности.

Такое рассогласование отражается на LT-размерности метрики, что может приводить к разным результатам.

У автора мощность = воздействие (U) х отклик (I), то есть как произведение напряжения на ток, как мощность в электротехнической проекции полной мощности (N), имеющие тем не менее одинаковую LT-размерность [L⁵T^-5].

В электротехнической проекции произведение воздействия (U) на отклик (I) определяет электрический поток энергии или электрическую проекцию N (U x I) полной мощности с размерностью [L⁵T^-5].

В уравнении полной мощности (N) произведение воздействия (N) на отклик (P + G) определяет квадрат полного потока энергии или квадрат полной мощности [L5T-5]2.

Здесь нет никакого противоречия, если принять во внимание, что автор рассматривает не полную мощность, а лишь одну из возможных её проекций. Можно было бы в качестве проекций полной мощности рассмотреть и другие воздействия и отклики: механические, акустические, оптические, термодинамические и другие.

Однако, все они являются проекцией закона сохранения полной мощности [L5T-5]=const в частные системы координат.

Следует заметить, что в общей теории устойчивого развития [7] выделяются три вида мощности, объединенные единым уравнением полной мощности.

Каждому виду полной мощности соответствует своя мощность в электрической цепи как произведение тока и напряжения, соответственно, на входе и выходе системы.

Уравнение полной мощности в электрической цепи может быть записано следующим образом:

N (U x I) = P (U x I) + G (U x I), [L5T-5], где N (U x I) – потребленная электрическая мощность на входе;

P (U x I) – произведенная электрическая мощность на выходе;

G (U x I) – мощность потерь (рассеиваемая мощность).

Расчет мощности в электрической цепи необходимо делать в соответствии с уравнением полной мощности, учитывая изменения всех трех её составляющих N, P, G при изменении связей под контролем уравнения полной мощности.

В таблице треугольниками показан пример связи воздействий, откликов и материи. В жидкости: если воздействием является давление [L2 T–4], (внутреннее воздействие, замкнутая система) а поток жидкости (скорость изменения объема) – откликом, [L3 T–1], то материю характеризует гидравлическое сопротивление, [L–1 T–3]. Связь показана толстыми линиями. Если воздействием является поток жидкости (внешнее воздействие, открытая система), а откликом – давление, то материю характеризует гидравлическая проводимость, [L1 T3], обратная к сопротивлению. Эта связь показана тонкими линиями. Аналогичные треугольники можно найти и для других предметных областей. Для электротехники они вырождаются в прямую линию.

Для создания сетевых моделей не меньшую роль играет структура. Сложные системы отличаются наличием большого количества элементов, соединение элементов образует структуру. Структуру трудно считать материей. Ее значение нельзя измерить приборами так, как это делается с физическими величинами. Понятиям структуры (симплексы, комплексы, замкнутые и разомкнутые пути) нет места в системе измерения физических величин, например в LT таблице Бартини-Кузнецова. Вместе с тем понятие структуры пронизывает все, что существует, как живые, так и неживые системы, на всех уровнях от масштабов микромира до космических масштабов.

Структура составляет основу пространства, которое Аристотель считал пустотой, в которую помещаются предметы, т.е. физические величины с их размерностью.

От ред. совета Б.Б.Е.: По-видимому, имеется ввиду, что сама LT-система как соединение элементов (величин) образует структуру. Однако, автор, на наш взгляд прав в том смысле, что численные значения структуры следует получать посредством вычисления по определенной схеме (уравнениям), а не посредством измерения той или иной величины.

Сама по себе LT-величина в её количественном выражении не определяет значение структуры, но как качественная определенность – определяет LT-границы класса систем, имеющих определенную структуру.

Эта структура может быть представлена, например, уравнением, связывающим её элементы, каждый из которых является частной LT-величиной как проекцией общей LT-величины, определяющей границы класса систем.

Например, структура систем, определяемых размерностью мощности [L5T-5]=const, может быть представлена уравнением:

·t-4 + L5T0 ·t-5.

L5T-5 = L5T-4 ·t-1 + L5T-3 ·t- 2+ L5T-2 ·t-3 + L5T-1

Данное уравнение описывает структуру, оставаясь в границах класса систем с размерностью [L5T-5]=const.

Двойственные сети – решение диалектического противоречия постулата Крона

Как было показано, реально постулат Крона об инварианте мощности не выполняется, поскольку мощность при изменении связей меняется, а вывод формул тензорного анализа сетей содержит недопустимое обращение прямоугольной матрицы. Однако его метод расчета цепей и машин дает правильные результаты. Получается диалектическое противоречие. Автор исследовал изменение мощности в цепи при изменении структуры, чтобы найти закон. Оказалось, что решение, в согласии с диалектикой, лежит в другой «плоскости». Рассеиваемая мощность меняется в одной цепи при изменении связей, но постоянна в сумме двух цепей: рассматриваемой цепи и цепи с двойственной структурой.

От ред. совета Б.Б.Е.: Этот крайне ответственный вывод автора нуждается в пояснении. Автор тщательно исследовал изменение рассеиваемой мощности, то есть произведений напряжений и токов в каждой свободной ветви электрической цепи. Аналогично для напряжений и токов в контурах связанной цепи. В ходе анализа обнаружил недопустимое обращение прямоугольной матрицы при выводе Г.Кроном формул тензорного анализа. При этом выявил, что метод Г.Крона дает, тем не менее, правильные результаты. И объясняет это наличием диалектического противоречия.

Далее автор для разрешения противоречия предлагает свой оригинальный метод, основанный на свойстве двойственности, прежде всего, математической структуры, далеко не всегда, на наш взгляд, согласованной с физической структурой, о чем будет сказано ниже. Тем не менее, метод очень интересный, но и трудоёмкий в расчетном смысле. По этой причине очень хотелось бы, чтобы автор подтвердил свой вывод на основе уравнения полной мощности П.Г.Кузнецова Все члены редакционного совета будут благодарны.

Фундаментальное свойство двойственности структуры выражает закон, который связывает матрицы преобразования сетей с двойственной структурой. Математически этот закон представляет собой постоянство метрических тензоров структуры в данном подпространстве и двойственном подпространстве. Это свойство двойственности самого пространства. По своей сути инвариант двойственности является причиной того, что существует закон сохранения потока энергии. Этот закон сохранения, следующий по физической размерности после закона сохранения энергии, является физико-структурным законом. Можно рассматривать закон сохранения потока энергии как причину существования свойства двойственности пространства. Тогда из него следует существование сетевых структур, расположенных в ненаблюдаемом пока двойственном пространстве.

Пример двойственных сетей дан на рисунке, по сути это одна сеть из двух частей (рис. 1).

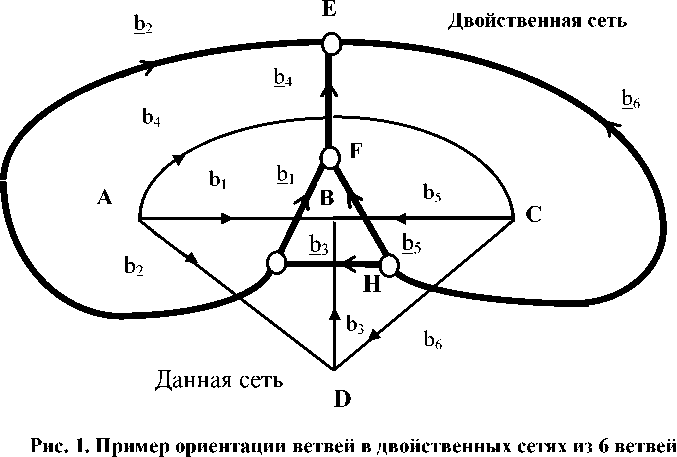
В сети двойственными являются замкнутые и разомкнутые пути, воздействия и отклики, сеть и двойственная к ней сеть (ее величины подчеркнуты). Если соединить две ветви, то два узла сливаются (их число уменьшается). Возникает новый независимый контур, растет размерность пространства замкнутых путей. Но исчезает разомкнутый путь, уменьшает размерность базиса разомкнутых путей. Общая размерность пространства путей сети не меняется, она равна количеству элементов – ветвей, т.е. n = m + j .

В двойственных сетях постоянны размерности дополняющих друг друга подпространств замкнутых и разомкнутых путей. Замкнутому пути в сети соответствует разомкнутый путь в двойственной сети, и наоборот: n = n , m + m = n, j + j = n . Слиянию двух узлов в сети соответствует разделение узла на два в двойственной сети, и наоборот. Свойства изменения структуры двойственных сетей показаны в таблице 2.

Таблица 2. Соответствие преобразований структуры двойственных сетей

	Сеть	Двойственная сеть
Тип соединения ветвей	параллельное	последовательное
Ориентация ветвей	встречная	согласованная
Преобразование структуры	слияние узлов	разделение узлов
– изменение соединений	J’ = J – 1	J ’ = J + 1
•    изменение контуров	возникает контур m’ = m + 1	исчезает контур m ’ = m – 1
•    изменение открытых путей	исчезает разомкнутый путь j = j’ + 1	возникает разомкнутый путь j = j’ – 1

От ред. совета Б.Б.Е.: Здесь речь идет о размерности в математическом смысле, а не в физическом.

Для двойственных сетей существуют инварианты. При изменении структуры двойственных сетей общая размерность подпространств замкнутых путей постоянная; общая размерность подпространств разомкнутых путей постоянная. Сумма метрических тензоров постоянна. Сумма токов в каждой ветви постоянная. Сумма напряжений на каждой ветви постоянная. Сумма мощностей, рассеиваемых в двойственных сетях постоянная. Сеть и двойственная сеть дополняют друг друга. Подпространства контуров и подпространства разомкнутых путей двойственных сетей в сумме имеют размерность полного пространства сети. Двойственные сети образуют единый объект в таком пространстве.

Матрицы преобразования путей базиса p α свободных путей к базису p β связанных путей – матрицу C β^α данной сети, и матрицу преобразования С α ⁰ = A 0 ^α , двойственной сети, которые даны на рисунке 1, представлены ниже:

α p1 0

p2 0

p3 0

p4 0

p5 0

p6 0

α

β p 1 0

p 2 0

p 3 0

p 4 0

p 5 0

p 6 0

p 1

1

–1

–1

m

p 1

–1

–1

j

p 2

–1

–1

–1

m

p 2

1

–1

1

j

p 3

1

–1

–1

m

p 3

–1

j

0 С α = p 4

1

j

0 С α = p 4

1

1

1

m

p 5

–1

j

p 5

–1

1

–1

–1

m

p 6

1

j

p 6

1

–1

1

m

Матрицы преобразования имеют блочный вид, т.е. с нулевым блоком выражения разомкнутых путей через замкнутые пути . Матрицы преобразования Крона выражают токи в связанной сети через токи свободных ветвей; они транспонированы по отношению к матрицам преобразования путей.

Свойства двойственности присущи самой структуре, даже если нет материи. Например, если сопротивления ветвей равны единицам ( Z = Y = I ), то инвариант двойственности связывает матрицу решения сети и матрицу решения двойственной сети:

• ^mC (^mC t ^mC)^{-1 m}C t + ^jA (^jA t ^jA)^{-1 j}A t = ^mC (^mC t ^mC)^{-1 m}C t + ^m C (^m C t ^m C )^{-1 m} C t = I, (17) где ^mC = ^j A – матрица преобразования замкнутых путей сети, или разомкнутых путей двойственной сети, а ^jA = ^m C – матрица преобразования разомкнутых путей сети, или замкнутых путей двойственной сети, I – единичная матрица. Слагаемые в данном соотношении представляют собой метрические тензоры соответствующих двойственных сетей, ветви которых имеют единичные веса. Это означает, что воздействие и отклик в таких

ветвях численно равны друг другу, они не оказывают сопротивления материи прохождению потока энергии. Это закон структуры, не связанный с материей. Сюда входят только матрицы преобразования путей.

Если ветви сети имеют веса-сопротивления (собственные и взаимные), выражаемые матрицей сопротивлений, метрического тензора Z ≠ I , ( Z = Y^-1 ), то инвариант двойственных сетей для замкнутых путей примет вид:

• ^mC (^mC t Z ^mC)^{-1 m}C t + Y ^m C (^m C t Y ^m C )^{-1 m} C t Y = Y = (Z) ^-1 , (18)

Для разомкнутых путей инвариант имеет двойственный вид, с заменой С на А , Z на Y . Инвариант связывает метрические тензоры двойственных сетей. Если в сети есть воздействие, то его компоненты расположены в базисе замкнутых (внутреннее воздействие) или разомкнутых (внешнее воздействие) путей. В данном случае инвариант – это постоянство квадрата величины вектора: часть вектора расположена в сети, часть в двойственной сети, но их сумма постоянна и не зависит от изменения соединений. Для вектора ^m d , например, заданного в замкнутых путях, формула преобразования контравариантных компонент при изменении структуры, полученная на основе инварианта двойственных сетей, имеет вид:

m d ₀ ^а = X + X = m d “ ” €/ + m d jA^Y' Y^ep = ( " €/ ) t^m d “ + C^ a' ) t Y^eP m d ^в , (19) где ^md ₀ ^α – компоненты вектора в свободных ветвях, а ^md _c ^α и ^m d _c ^α – компоненты вектора в связанных двойственных сетях. Нельзя непосредственно получить компоненты вектора ^m d , для связанной сети по их значениям в свободных ветвях, поскольку в связанных ветвях они распадаются на совокупность компонент вектора в двойственных сетях и только в сумме дают компоненты полного вектора.

С точки зрения физики «вектор» можно рассматривать как совокупность источников напряжения, ЭДС (в базисе контуров), или как совокупность источников тока (в базисе открытых путей).

Поток энергии, численно равный мощности, рассеиваемой в сети, можно наглядно представить круговой диаграммой как красно-синий детский «мячик», до половины погруженный в «воду». Получается, что двойственная сеть должна располагаться в некотором двойственном пространстве, «параллельном» наблюдаемому нами пространству.

Площадь темной (красной) половины такого мячика соответствует мощности (или квадрату величины вектора) в замкнутых путях как данной, так и двойственной сети, а площадь светлой (синей) половины – мощности в разомкнутых путях. При изменении структуры мощность в двойственных цепях меняется. Это можно представить пропорциональным изменением площадей разных цветов при вращении двухцветного мячика, между границами наблюдаемого и ненаблюдаемого пространства, где:

• •    «воздушная» среда представляет наблюдаемое пространство;

• •    «водная» среда представляет двойственное пространство.

Вращение «мячика», представляющего собой диаграмму изменения мощности, меняет доли красного и синего цвета над (и под) поверхностью раздела двух сред. Сумма площади красного цвета (мощность внутренних источников, т.е. источников напряжения, ЭДС) над и под поверхностью (в данной и двойственной цепи) постоянна – соотношение (17). Сумма площади синего цвета (мощность внешних источников, т.е. тока) над и под поверхностью постоянна (18). Сумма площади красного и синего цвета над поверхностью, а также сумма площади красного и синего цвета под поверхностью, постоянны. При изменении структуры двойственных цепей, рассеиваемая мощность, меняется, но согласованно, так, что остаются постоянными четыре суммы в базисах замкнутых путей и разомкнутых путей. Эти суммы можно разделить на инварианты в пределах одной цепи, т.е. инвариант «по горизонтали диаграммы» и на инварианты в двух двойственных цепях, т.е. инвариант «по вертикали диаграммы», а именно:

• •    инварианты «по вертикали диаграммы»:

o  базис замкнутых путей – внутреннее (контурное) возбуждение, данная сеть и двойственная сеть (темная половина), замкнутые сети;

o базис разомкнутых путей – внешнее (узловое) возбуждение, данная сеть и двойственная сеть (светлая половина), открытые сети;

• •    инварианты «по горизонтали диаграммы»:

o данная сеть, контурное возбуждение и узловое возбуждение (верхняя половина);

o двойственная сеть, узловое и контурное возбуждение (нижняя половина).

Постоянство суммарной рассеиваемой мощности при изменении структуры двух двойственных цепей – это проявление закона сохранения потока энергии. Полная диаграмма изменения мощности при изменении структуры данной и двойственной сетей, в которых заданы источники энергии двух типов, представлена на рисунке.

Рассмотрим подробнее виды инварианта мощности. Как отмечалось, диаграмма показывает два вида двойственности сетей и инварианта мощности (рис. 2). Для каждого из них инвариантом является площадь полукруга, представляющая два вида мощности. Один вид инварианта – «по вертикали», т.е. потоку энергии соответствует один вид путей, один вид источника, но две сети.

Мощность постоянна в двух двойственных сетях при изменении структуры, как для замкнутых путей, так и для разомкнутых путей. Соответственно, для внутренних источников (напряжения) замкнутых систем и для внешних источников (тока) открытых систем. Здесь работает двойственность структуры двух цепей (сетей).

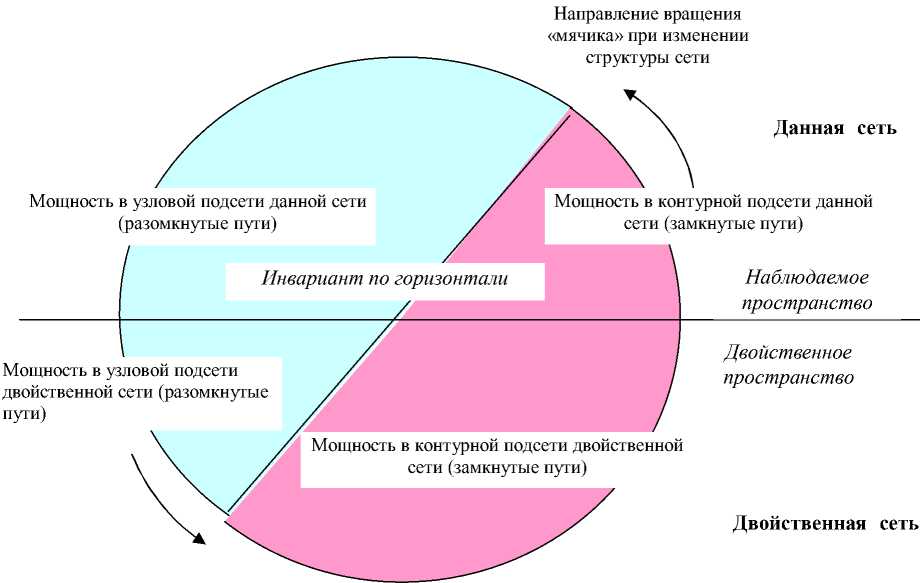
Рис. 2. Диаграмма изменения мощности в двойственных цепях при изменении структуры

Другой вид инварианта – «по горизонтали», т.е. потоку энергии соответствуют два вида путей, два вида источников, но одна сеть. Это постоянство рассеиваемой мощности в одной сети (цепи) в сумме от внутренних источников и внешних источников. Это при условии, что мощности источников в каждой ветви равны друг другу, либо равны нулю. Если источники тока и напряжения в ветви не равны друг другу, то рассеиваемые от них мощности все равно подчиняются инварианту двойственных сетей, хотя соответствующая диаграмма не будет столь наглядной. Здесь работает двойственность замкнутых и разомкнутых путей в структуре одной цепи.

Двойственное пространство располагается (существует) «параллельно» в любой точке наблюдаемого пространства и участвует в преобразовании потоков энергии при их движении по путям, создаваемым структурой. По своей сути двойственные пространства в совокупности составляют единое пространство. Таким образом, параллельное пространство располагается вокруг нас, оно должно контактировать с объектами, расположенными в «нашем», наблюдаемом пространстве, при распространении потоков энергии, проявляя себя при изменении структуры систем, по которым энергия распространяется.

Противоречие двойственных сетей – непланарные графы

Двойственные сети решают проблему инварианта мощности, но в них самих есть диалектическое противоречие , которое состоит в том, что для непланарного графа нельзя построить двойственного графа. А это значит, что для таких структур нет двойственной сети. Эта фундаментальная проблема рассматривается в топологии, где она принимается как факт. Таким образом, двойственные отношения сложнее, чем это может показаться. На эту особенность указал автору в 1984 г. В.А.Горбатов. Двойственные сети дают интересную информацию для исследования, но проблема остается, и требует своего решения.

С одной стороны, непланарные графы создают проблему для инварианта двойственных сетей; постоянства мощности двойственных цепей, закона сохранения потока энергии. Как только изменение структуры сети приводит к возникновению в ней непланарного графа,  двойственная сеть как бы перестает существовать, ее нельзя представить наглядно, измерить результаты расчета. Но при дальнейшем изменении структуры непланарность исчезает, и снова возникает двойственная сеть. Свойства двойственности «возвращаются». Должна существовать какая-то, еще не известная закономерность, с которой связаны такие эффекты.

С другой стороны, возникновение проблемы указывает на новое противоречие, а разрешение противоречий дает развитие. Разрешение противоречия между постулатом об инварианте мощности Крона и реальным изменением мощности при изменении структуры открыло ранее не известные двойственные сети. Найден инвариант, связывающий структуру двух двойственных сетей и ее изменения. Только для двух двойственных цепей выполняется инвариант мощности, а не для одной цепи, как постулировал Крон.

Выход в «другое» измерение разрешил противоречие Крона в соответствии с принципами диалектики. Разрешение противоречия непланарности двойственных сетей может открыть новые свойства двойственных сетей, пространства и структуры.

В топологии для доказательства того, что непланарный граф не имеет двойственного графа, используются два известных непланарных графа Куратовского, а именно, K 3,3 и K 5 ( Куратовский , 1966). Сначала доказывают, что для этих графов двойственные графы не существуют, а затем доказывают, что любой непланарный граф содержит либо K 3,3 , либо K 5 . Если при изменении структуры сети, пусть даже очень большой, в ней, в какой-то ее части, возникает один из этих графов (или оба), то двойственная сеть (граф) перестает существовать. Однако если при дальнейшем изменении структуры эти графы меняют свою конфигурацию на любую другую, то двойственная сеть снова существует.

Таким образом, именно эти два графа лежат в основе проблемы отношений между двойственной структурой сетей и непланарностью. Первый из них – это так называемый «двудольный» граф, в котором каждая из трех «верхних» вершин связана с каждой из трех «нижних» вершин. Всего такой граф содержит 9 ветвей-ребер. Второй представляет собой пятиконечную звезду, связанную по периметру, а точнее – это полный граф на пяти вершинах, т.е. каждая из вершин связана со всеми остальными вершинами ребрами (ветвями). Всего здесь 10 ветвей-ребер. Следовательно, пространство одной из таких непланарных сетей имеет 9 измерений, а другой – 10 измерений.

Граф K 3,3 можно рассматривать как три отрасли, связанные поставками , т.е. он может входить в структуру экономических систем, имея важное практическое значение (рис. 3).

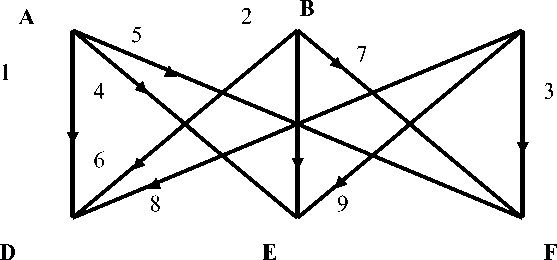
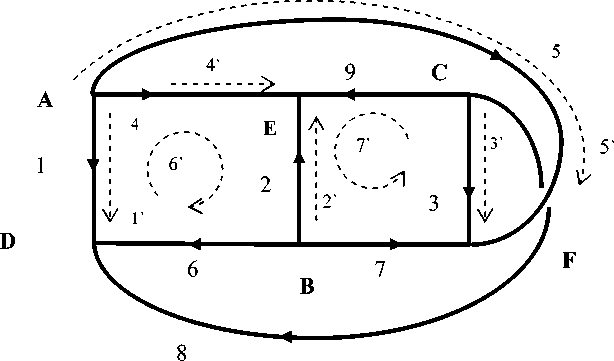
Рис. 3. Граф К 3,3 в традиционном представлении, и в представлении, демонстрирующем его непланарность

Сеть, структура которой представляет собой непланарный граф К3,3, имеет количество ветвей n = 9, узлов J = 6, число независимых подсетей s = 1, независимых разомкнутых путей J – s = 6 – 1 = j = 5, независимых замкнутых путей (контуров) m = 5. Все выбранные пути, в том числе не показанные на схеме, легко определить по ненулевым элементам матрицы Са“:

К з,з :    С_а- ^а =

6    7    8    9    1    2    3    4    5

6`	1				–1	–1		1		m
7`		1		1		–1	–1			m
8`			1		–1		–1		1	m
9`				1			–1	–1	1	m
1`					1					j
2`						1				j
3`							1			j
4`								1		j
5`									1	j

Выделены блоки, относящиеся к замкнутым и разомкнутым путям. Путь 8` состоит из ветвей непланарного контура, который здесь нельзя расположить в одной плоскости.

Сначала построим структуру двойственных сетей к непланарным графам, используя свойства ортогональности матриц преобразования путей. Для этого получим матрицу преобразования путей, ортогональную к данной матрице. Это матрица преобразования путей двойственной сети. Строки в этой матрице перечисляют ветви, входящие в независимые замкнутые и разомкнутые (базисные) пути двойственной сети. Соединяя ветви в той последовательности и с той ориентацией, которая указана в строках ортогональной матрицы преобразования, попытаемся построить двойственную сеть.

Используя ортогональные матрицы преобразования A ^a _a = (С_а-^а )Г¹ , рассчитаем матрицы решения сетей непланарных графов и двойственных к ним сетей. Затем рассчитаем непланарные графы-сети с произвольным вектором воздействия, получим значения откликов на ветвях, и проверим их на выполнение законов Кирхгоффа. Полученные решения для двойственных сетей, вместе с их матрицами преобразования С «^а = А ^а _а используем для того, чтобы понять, как устроена структура двойственного графа к непланарному графу, который не должен существовать. Получается, что два непланарных графа по своей структуре двойственные друг к другу, но весьма необычным образом. Так, что одна ветвь принадлежит при двойственном переходе одновременно к двум графам.

Матрица преобразования путей двойственной сети транспонирована к обратной матрице путей заданной сети. Это матрица преобразования путей в двойственном графе K₃ , ₃ :

					6	7	8	9	1	2	3	4	5
				6 `	1									j
				7 `		1								j
				8 `			1							j
				9 `		–1		1						j
(Ca^t"1 =	A a a '	α Ca'	=	1 `	1		1		1					m
				2 `	1	1				1				m
				3 `			1	1			1			m
				4 `	–1	–1		1				1		m
				5 `		1	–1	–1					1	m

Для построения структуры сети используем строки 1`–5`, которые соответствуют контурам. Например, путь 1`показывает, что ветви 1, 6 и 8 должны образовать замкнутый треугольник, в котором они ориентированы одинаково, т.е. последовательно. Аналогично соединяются ветви по остальным путям, каждый из которых должен добавлять хотя бы одну новую ветвь к уже охваченным ветвям. Разомкнутые пути контролируют открытую часть сети, т.е. узлы, через которые происходит взаимодействие с внешним миром. Например, путь 6` начинает с того, что соединяет узлы К и М. Каждый следующий разомкнутый путь добавляет хотя бы один узел.

Построенная по этой матрице соответствующая сеть представлена на рисунке 4.

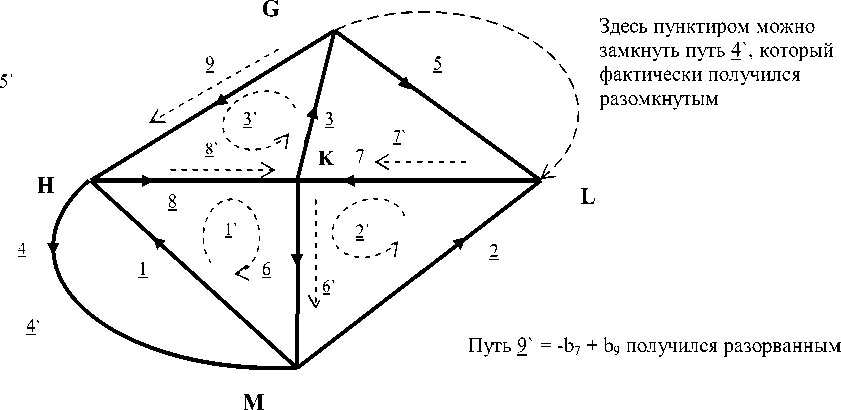
Рис. 4. Граф, который соответствует матрице А, ортогональной к матрице путей графа К 3,3 , похож на граф К 5 , но ему не хватает одной ветви для замыкания пути 4 `

Можно заметить, что для этой сети, структура которой не должна существовать, матрица преобразования существует и имеет вполне определенный вид. Сеть, которая показана на рисунке, построена так, как указывает состав ветвей в путях этой матрицы. Граф этой сети похож на граф К 5 , но ему не хватает одной ветви для замыкания пути 4 `. Дело в том, что один путь, замкнутый в соответствии с матрицей преобразования, оказался разомкнутым. Этот путь 4 `состоит из ветвей 6 , 7 , 9 и 4 . Чтобы он стал замкнутым, нужна еще одна ветвь, которая бы замыкала узлы G и L . Если такую ветвь добавить, то двойственная сеть к графу К 3,3 превратится в сеть, похожую на граф К 5 . Эта недостающая для замыкания пути 4 ` ветвь показана пунктиром в правой части рисунка.

Особенностью разомкнутых путей является то, что три пути полученного базиса проходят каждый по одной ветви, но один путь, а именно путь 9` оказывается разорванным. Путь 9` состоит из ветвей +9 и –7, которые в этой структуре, вообще не связаны друг с другом своими границами. Это допустимо по определению пути, но это указывает на то, что в двойственной сети к непланарной структуре происходит что-то необычное. Таким образом, при заданном выборе путей, в двойственной сети один замкнутый путь формально оказался разомкнутым, а один разомкнутый путь стал разорванным, т.е. состоит из ветвей, которые не соединены друг с другом.

Аналогичная картина происходит и с двойственной сетью к графу К 5 , но с тем отличием, что здесь одна ветвь оказывается «лишней» в сети, построенной на основании ортогональной матрицы преобразования. Можно сказать, что эти непланарные графы двойственны друг другу, но несколько странным образом. Таким образом, что при этом одна ветвь оказывается как бы между этими графами. В одной из непланарных двойственных сетей эта ветвь избыточная, а в другой недостающая.

Пусть наложенный вектор ^m d (источник напряжения) имеет заданную компоненту в одной из свободных ветвей, например, ^m d ⁰8 = 1:

6     7     8     9     1     2     3     4     5

Квадрат величины вектора ^md в заданной сети равен:

I m d ' I ² = m P' = (4 + 1 + 16 + 4 + 4 +1 + 4 + 1 + 1) /81 = 36/81 = 4/9 = 0,4444.

Это мощность, рассеиваемая в сети со структурой, соответствующей непланарному графу, при задании единственного внутреннего источника, т.е. источника напряжения.

Квадрат величины вектора ^m d в двойственной сети непланарного графа K 3,3 равен:

I m d ' l ² = m P' = (4 + 1 + 25 + 4 + 4 +1 + 4 + 1 + 1) /81 = 45/81 = 5/9 = 0,5556.

Здесь выполняется условие инвариантности квадрата величины вектора в двойственных сетях, а именно:

I m d ⁰|² = I m d ' l ² + I m d ' l ² = 0,4444 + 0,5556 = 1,0000.

Более того, по каждой ветви в двойственных сетях сумма компонент равна источнику воздействия в данной ветви, например, в ветви b 8 ^m d c⁸ + ^m d c⁸ = 0,44 + 0,56 = 1 = ^m d ⁰8 . Таким образом, выполняется условие постоянства компонент по каждой ветви при любых соединениях в двойственных сетях, в том числе и в случае данного непланарного графа.

При проверке закон Кирхгофа в узлах для сети непланарного графа полностью выполняется, а для двойственной сети в узлах G и L – не выполняется.

При проверке закон Кирхгофа для напряжений в контурах для обеих сетей полностью выполняется, т.е. есть баланс воздействий и откликов по каждому контуру. В контуре 4 ` хотя формально и выполнено условие закона Кирхгофа, в соответствии с результатами расчета, однако на схеме двойственной сети он не замкнут, т.е. не является контуром.

76 Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление» www.rypravlenie.ru                                             том 7 № 3 (12), 2011, ст. 2

Выпуск подготовлен по итогам Международной конференции по фундаментальным проблемам устойчивого развития в системе природа – общество – человек (24 и 25 октября 2011 г., проект РФФИ №11-06-06128-г).

Непланарный граф K 5 (полный граф на 5 узлах, где каждый узел соединен с каждым другим) представлен на рисунке 5. Он же развернут на плоскости так, чтобы показать его самопересечение. Этот граф имеет ветвей n = 10, узлов J = 5, независимых разомкнутых путей j = 4, независимых замкнутых путей (контуров) m = 6.

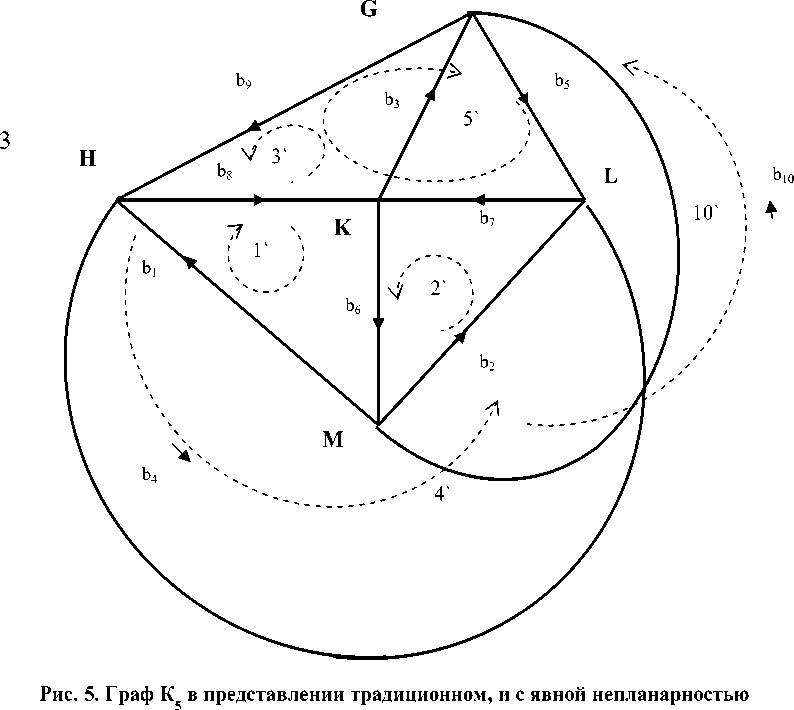
Обозначения и направления ветвей в сети графа выберем максимально близкие с двойственной сетью графа K 3,3 . Для этого переключим ветвь b 4 с узла M на узел L , и добавим ветвь b 10 .

Матрица преобразования путей данной сети представлена ниже:

K 5 :

C α α `

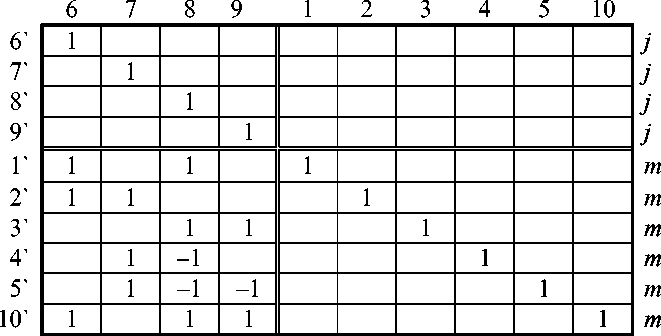
В этой матрице выделены блоки, относящиеся к замкнутым и разомкнутым путям.

Ветви и пути также перенумерованы здесь для того, чтобы максимально сопоставить сети и двойственные сети, соответствующие непланарным графам.

Путь 4` выбираем другим, поскольку в прототипе этой матрицы (для двойственной сети графа K 3,3 ) он оказался разомкнутым. Все равно один из путей, которые согласно матрице преобразования должны быть замкнутыми, на схеме сети станет разомкнутым.

Попытаемся построить двойственную сеть к сети непланарного графа, используя ее матрицу преобразования, которая является ортогональной к матрице исходной сети. Может быть, матрица преобразования путей двойственной к непланарной сети вырожденная? Нет, она существует, и является матрицей преобразования путей Cα`α = Aαα = (Cα`α)t–1, строки- пути которой показывают, как связаны свободные ветви в двойственную сеть. Таким образом, матрица преобразования двойственной сети для графа K5 имеет вид:

		6	7	8	9	1	2	3	4	5	10
	6 `	1				-1	-1				-1	m
	7 `		1				-1		-1	-1		m
	8 `			1		-1		-1	1	1	-1	m
	9 `				1			-1		1	-1	m
(C α ` α ) t -1 = A α ` α =    C α ` α =	1 `					1						j
	2 `						1					j
	3 `							1				j
	4 `								1			j
	5 `									1		j
	10 `										1	j

Эту матрицу будем использовать для построения структуры двойственной сети по отношению к непланарному графу. Такая структура оказывается несколько неожиданной. Из контурной части матрицы двойственной сети можно построить четыре контура, которые связывают ветви этой сети в некоторую структуру.

Разомкнутые пути в этой двойственной сети, как показывает узловая подматрица, включают в себя по одной ветви, которые соединяют по два узла, постепенно охватывая все узлы сети. Например, путь 1 `: <sup>j</sup> p ` 1 = b 1 . Аналогично пути 2 `– 5 ` и путь 10 `.

Замкнутые пути 6 `, 7 ` и 9 ` задают три контура-квадрата, соединяя 9 из 10 ветвей.

Путь 8 `, добавляя к этому ветвь b 8 , задает такой набор ветвей, что все они, кроме ветви b 3 , составляют контур из ветвей, уже вошедших в другие контуры. Этот путь выделен на рисунке жирным пунктиром. Т.е. данный контур проходит замкнутый путь как бы внутри сети, а, кроме того, проходит и по ветви b 3 . Таким образом, эта ветвь оказалась в данном варианте структуры подвешена к контуру, превращая данный путь в смешанный, т.е. содержащий и замкнутый путь, и разомкнутый путь.

На рисунке 6 представлен вариант двойственной сети к непланарному графу K 5 , и ее структура практически повторяет структуру графа K 3,3 . Исключением является ветвь b 3 . Эта ветвь здесь «лишняя», поскольку в первом непланарном графе 9 ветвей, а во втором, рассматриваемом здесь, – 10 ветвей. Эта ветвь играет особую роль, например, по отношению к потокам энергии через сеть. В структуре сети особенность b 3 состоит в том, что по составу путей, в которые она входит, она должна иметь ориентацию как в одном направлении, так и в другом направлении. То есть, как нетрудно видеть, для пути 8 ` она должна быть направлена вверх, а для пути 9 ` – вниз.

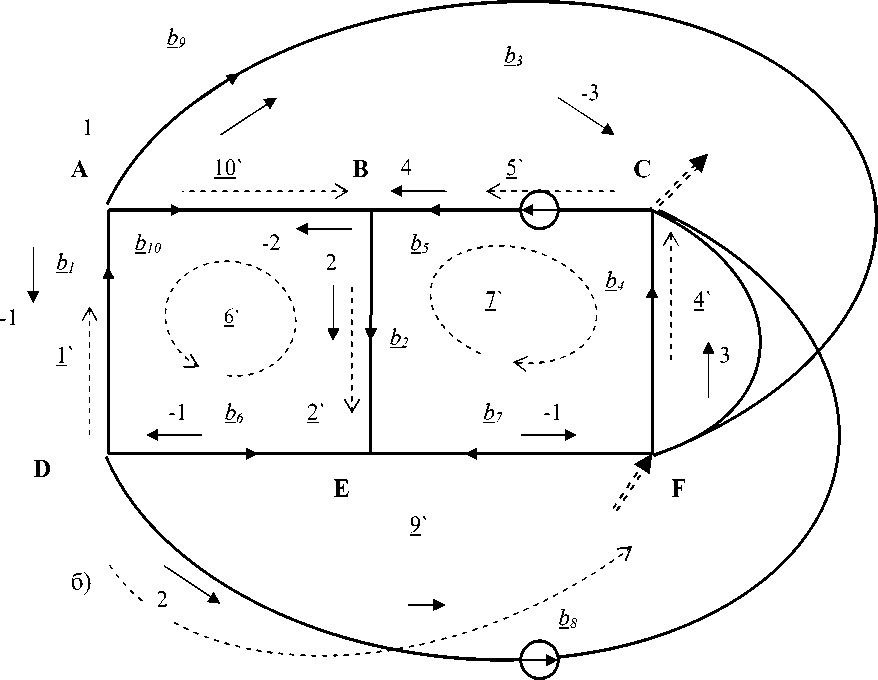
Рис. 6. Результаты расчета двойственной сети к непланарному графу K 5

Пусть наложенный вектор (источник напряжения) ^m d имеет компоненту в той же свободной ветви, что и в предыдущем примере, ^md⁰ 8 = 1 :

6     7     8     9     1     2     3     4     5    10

1

m0

d _α =

Проведем расчет компонент откликов этого вектора в связанной сети графа K 5 для подматрицы преобразования ^mC , при Z = I , умножая матрицу решения на вектор воздействия: ^md с ^α = Y c ^md⁰ α . Получим равные друг другу значения ковариантных и контравариантных компонент ^md с ^α = ^md^с α вектора в ветвях связанной сети:

m _dс α

6     7     8     9     1     2     3     4     5    10

m _d с _{α =}

1

-1

3

1

1

0

1

-1

0

0

Квадрат величины вектора ^md в заданной сети равен:

I m d ' l ² = ^mP' = (1 + 1 + 9 + 1 + 1 +0 + 1 + 1 + 0 + 0) /25 = 15/25 = 3/5 = 0,6.

Это мощность, рассеиваемая в сети со структурой, соответствующей непланарному графу K 5 , при задании одного внутреннего источника, т.е. источника напряжения.

Проведем расчет компонент откликов в связанной двойственной сети для графа K 5 , которая построена по матрице преобразования ^m C , умножая матрицу решения на вектор воздействия: ^m d с ^α = Y c ^md⁰ α . Получим равные друг другу значения ковариантных и контравариантных компонент ^m d с ^α = ^m d ^с α вектора в ветвях связанной сети:

m _dс α

6     7     8     9     1     2     3     4     5    10

m _d с _{α =}

-1

1

2

-1

-1

0

-1

1

0

0

Квадрат величины вектора ^m d в двойственной сети равен:

I m d ' l ² = ^mP' = (1 + 1 + 4 + 1 + 1 +0 + 1 + 1 + 0 + 0) /25 = 10/25 = 3/5 = 0,4.

Это мощность, рассеиваемая в двойственной сети к непланарному графу, при задании одного источника напряжения. Выполняется инвариант двойственных сетей, или закон постоянства мощности в двойственных цепях, для непланарного графа на 10 ветвях:

I m d ⁰|² = I m d ' l ² + I m d ' l ² = 0,6 + 0,4 = 1,0.

Проверка найденных решений показывает, что для сети непланарного графа закон Кирхгофа для токов полностью выполняется, а для двойственной к ней сети, построенной по ортогональной матрице преобразования путей, в двух узлах С и F - не выполняется.

Закон Кирхгофа для напряжений выполняется. Хотя можно было предположить, что «лишним» окажется значение напряжения в ветви 3 , которое равно – ^m d ^с 3 = + 3/5, поскольку именно эта ветвь по построению сети оказалась вне контура ветвей 1 , 4 , 5 , 8 , 10 , оставшись как бы «подвешенной» к контуру в виде отдельной ветви. В конфигурации данного пути ветвь b 3 оказалась разомкнутой. При этом именно на границах этой ветви не выполняется баланс токов в узлах двойственной сети. Создается впечатление, что через ветвь 3 проходит дополнительный поток от некоторого « внешнего » воздействия. Это воздействие показано на рисунке двойным пунктиром; оно выглядит как ток, входящий в узел F и выходящий из С .

Для двойственной сети, построенной по ортогональной матрице преобразования путей, в контуре 8 ` выполняется условие закона Кирхгофа для результатов расчета, но на схеме двойственной сети этот путь фактически не замкнут. Т.е. путь не является контуром, но значение в «висячей» ветви приводит сумму напряжений в контуре к балансу с суммой напряжений заданных источников. Вместе с тем рассеиваемые мощности в этих сетях удовлетворяют инварианту двойственных сетей, т.е. их сумма равна сумме мощностей источников в свободных ветвях.

Таким образом, получим, что два основных непланарных графа, которые присутствуют во всех других непланарных графах, могут быть двойственными друг другу. При этом одна ветвь, на которую они отличаются, оказывается как бы подвешенной в двойственной структуре, расположенной отдельно от самой сети.

Итак, при анализе поведения непланарных графов и их возможных двойственных сетей, возникает противоречие . Оно состоит в том, что двойственные к непланарным графам сети дают такие структуры, в которых выполнение законов Кирхгофа в замкнутых и разомкнутых путях противоречит полученной структуре сетей. Это говорит о том, что структура двойственных сетей к непланарным графам, должна иметь более сложную конфигурацию , чем двойственные сети, которые получались обычно для сетей, соответствующих планарным графам.

Вектор потока энергии и противоречия размерностей физических величин

Павлов вырабатывал у собаки рефлекс слюноотделения на показ круга (собаку кормили), а на показ овала – рефлекс страха (собака получала слабый удар током). Затем перед носом собаки лист незаметно поворачивали, и круг превращался в эллипс. Сильные духом собаки отворачивались, слабые – срывались в истерику.

Этот пример П.Г. Кузнецов приводил как виды реакции на демонстрацию диалектических противоречий.

Знаем ли мы, что такое поток энергии? С физической размерностью потока энергии связано противоречие . Казалось бы, это понятие пронизывает все мироздание. Вместе с тем в физике понятие потока энергии характеризуют мощностью. Мощность – физическая величина, измеряемая отношением работы к промежутку времени, в течение которого она произведена ( ФЭС , с. 440). В случае непрерывной среды или поля вводят понятия плотности энергии, т.е. энергии в единице объема и плотности потока энергии, равной произведению плотности энергии на скорость ее перемещения.

LT таблица дает целочисленные степени размерностей физических величин. Получается, однако, что вектор потока энергии имеет дробную физическую размерность. Возможно, что это свидетельство в пользу двойственной структуры пространства.

Существование открытых и замкнутых систем, различная роль в них продольных и поперечных величин как воздействий и откликов, придает LT таблице новое качество, связанное со структурой. Сама структура не входит в данную таблицу. Новое качество связано с пространствами замкнутых и разомкнутых путей, геометрическая размерность которых меняется при изменении структуры сети, но остается постоянной в двух двойственных сетях, как и рассеиваемая мощность.

Продольные величины в базисе путей играют роль контравариантных компонент вектора потока энергии, который обозначим d . Это означает, что при изменении базиса путей, системы координат, они преобразуются с помощью матрицы, обратной к матрице преобразования векторов базиса. Поперечные величины в базисе путей играют роль ковариантных компонент вектора потока энергии. Это означает, что при изменении базиса путей, системы координат, они преобразуются с помощью такой же матрицы, как матрица преобразования векторов базиса.

Вектор потока энергии. Скалярное произведение ковариантных и контравариантных компонент равно, как известно, квадрату величины вектора. Произведение продольных и поперечных величин по физической размерности и по величине равно мощности P . Продольные и поперечные величины и есть ковариантные и контравариантные компоненты вектора, следовательно, квадрат величины вектора потока энергии d ² равен мощности, т.е. его физическая размерность есть

[ P ] = [ d ²] = [L⁵ T^–5].                                     (20)

Тогда сам этот вектор должен иметь размерность, равную корню квадратному из размерности мощности, т.е. получается, что вектор потока энергии имеет дробные степени физической размерности :

[ d ] = [L^5/2 T^–5/2].                                              (21)

С точки зрения логики построения LT таблицы дробных степеней размерности быть не должно. Это указывает на необычное положение вектора потока энергии по отношению к понятиям пространства и времени, по отношению к другим физическим величинам. Действительно, в основу построения таблицы взяты фундаментальные понятия – длина (протяженность) L , т.е. основная характеристика пространства, и время T (длительность). Остальные величины располагаются в таблице как та или иная степень этих основных величин, т.е. пространства и времени. Если говорить точнее, то наблюдаемого нами в настоящее время пространства, и измеряемого нами в данной точке времени. Такая странность в размерности вектора потока энергии может быть причиной того, что это понятие в физике применяется недостаточно широко. Другой причиной является то, что это понятие, помимо физической составляющей, имеет структурную составляющую.

От ред. совета Б.Б.Е.: На наш взгляд, нет никакого противоречия с дробными степенями. Всё гораздо проще. Произошло смешение размерностей вектора геометрического Х и вектора физического Р (мощность).

Размерность вектора геометрического: [X] = [L^RrP].

Размерность вектора физического (мощности): [P] = [L^ST^S],

Квадрат вектора: [d] = [X²] = [L^2RTj.

Квадрат вектора мощности: [P] = [L¹⁰T¹⁰].

Отсюда следует, что вектор потока энергии имеет размерность мощности [P] = [L 5 T⁵ ] , а не дробные степени [L^5/2 T^–5/2].

Для обеспечения соразмерности потока пространственного с размерностью [L⁵T⁰] с потоком энергии [L 5 T 5 ] необходим оператор А с размерностью [L 0 T 5 ] . Физически оператор А представляет частотный генератор, обеспечивающий спиральное раскручивание тора [L 0 T⁵ ] с угловой скоростью [L 0 T ¹ ]⁵ .

Появление из приведенных выше рассуждений физической величины с дробной физической размерностью по отношению к пространству и времени расходится с предположением о неизменной фундаментальности этих основ. Или указывает на то, что принимаемое до сих пор предположение о незыблемой фундаментальности пространства и времени является необходимым, но не достаточным . Достаточность возникает из инвариантов двойственности . Мощность (поток энергии) остается постоянной (при заданных источниках энергии) при изменении структуры в двойственных сетях. При этом одна сеть располагается в наблюдаемом пространстве, а другая – в двойственном, не наблюдаемом, дополняющем наблюдаемое пространство до целого пространства.

Расщепление одного пространства на два взаимно дополнительных, двойственных пространства, восстанавливает размерность потока энергии до целочисленных степеней. Поток энергии расщепляется между двумя такими пространствами, в которых при изменении структуры остается постоянной сумма независимых замкнутых путей и разомкнутых путей. Одна часть потока располагается в соответствующих путях сети одного пространства, а другая часть – в дополняющих путях двойственного пространства. В каждой из частей поток энергии имеет размерность с дробными степенями, а их единство, полная сеть, дает размерность потока энергии с целыми степенями.

Можно ожидать, что по мере увеличения знания о мире, как пространстве и времени, будут обнаружены другие инварианты, более высокого порядка, чем закон сохранения потока энергии, связанный с двойственными структурами. Эти инварианты позволят найти другие свойства пространства протяженности (длины) и пространства длительности (времени). Они дополнят отношения двойственных сетей другими, более гармоничными и многомерными отношениями. При этом процесс познания сложности пространства протяженности и длительности (а только их мы измеряем в наших наблюдениях) является бесконечным во всех направлениях. Здесь рассматривается только один из первых шагов этого процесса, который дает математические основы для выхода за пределы наблюдаемых измерений физического пространства .

Вот так обстоят дела с противоречиями в основах. Или как вам будет угодно .

ПослесловиеОтклик автора на комментарий Ред.Совета Б.Б.Е. (с. 64.)

Дело не в прямоугольных матрицах преобразования, и не автор это обнаружил. А еще Б.Гоффман (B. Hoffmann) писал об этом в сборнике докладов семинара, посвященного памяти Г.Крона (Gabriel Kron and System Theory, 1973), причем ссылаясь на период до их знакомства. Прямоугольные матрицы преобразования были «красной тряпкой» для всех критиков Крона, начиная с 30-тых годов. Как раз Гоффман и удивился тому, что происходит недопустимое: мощность не сохраняется, обращаются матрицы прямоугольные, да и группу они по этой причине не образуют (а Крон писал о группе матриц преобразования), а метод расчета Крона дает правильные результаты. Даже благожелательно настроенные к работам Крона ученые выражали недоумение, но автор ни разу не читал, чтобы они видели в этом диалектику с необходимостью разрешения проблемы в другом измерении.

Автор провел немало расчетов, пытаясь обосновать метод Крона, полагая, что другие его не понимают. В 70-80-тые годы расчеты сетей (цепей) в ручном режиме были трудоемкими. В свое время, в 80-тых годах был создан комплекс программ, реализован на языке ПЛ/1, на перфокартах, конечно. Было сделано более сотни расчетов разных сетей. На ЭВМ ЕС 1045 в организации у В.И.Белякова-Бодина по ночам, когда давали машинное время ( трудоемкости расчетов сегодня уже нет – при современных пакетах программ МатЛаб, Эксель и т.д. все это могут повторить не вставая со стула ).

Мысль о противоречии и диалектике пришла автору постепенно. Когда он, следуя Крону, пытался доказать, что мощность не меняется при переходе от простейшей к соединенной сети, с помощью ортогональных сетей («Тензорный анализ сетей», глава 16). Крон писал, что если в сети связанной считать, что все пути остались контурами, как в простейшей сети, то матрицы преобразования квадратные, а мощность не меняется. Оказалось, что да не меняется, но решение сети не правильное – полученные токи и напряжения, измеримые величины на ветвях, не подчиняются законам Кирхгофа. Это потому, что полагая, что все базисные пути остались контурами, т.е. не изменились, мы остаемся в рамках чисто контурной сети, которая эквивалентна простейшей сети.

Вот и появилось противоречие – либо мощность постоянная (инвариант), но токи и напряжения на ветвях не являются решением. Либо мощность получается не постоянная (не инвариант), но токи и напряжения на ветвях являются решением. А при этом формулы расчета сети, т.е. этих самых токов и напряжений на ветвях, выводятся в предположении инварианта мощности!

Автор понял, что здесь что-то не так, и стал искать какую-нибудь закономерность изменения мощности при изменении структуры сети . Автора в МИФИ учили экспериментальной физике, поэтому он знал, что надо упростить, зафиксировать все параметры-факторы, чтобы искать чистую закономерность изменения одного параметра от изменения другого параметра. Сеть из четырех ветвей можно соединить так, что будет два контура (для источников напряжения) и две пары узлов (для источников тока). Это уже не числа, но и матрицы порядка всего лишь два на два, которые легко обратить (обращали руками и матрицы 3х3, и 4х4, но пока это делаешь, забудешь с чего начал, и куда шел). Значения источников тока и напряжения автор выбрал равными единицам, значения сопротивлений (импедансов), тоже равными единицам, и без взаимных импедансов, чтобы матрица простейшей сети была диагональная.

Этот пример, как и много других, был рассчитан автором в Рабочем журнале № 7, и подробно рассмотрен в главе 2 книги «Тензорная методология в теории систем», 1985 год.

Вот с такой предельно простой моделью автор и проводил расчеты, когда вечером 15 ноября 1981 года обнаружил, что мощность в контурной сети равна 2/5, в узловой сети 18/5, в сумме равна 2/5 + 18/5 = 20/5 = 4. А это и есть мощность в простейшей сети! И сразу «открылась бездна, звезд полна, звездам числа нет, бездне – дна!». Стало ясно, что открылось окно в другой мир, где каждой сети нашего мира соответствует сеть с двойственной структурой. Так устроен мир, но как построить эту двойственную сеть из другого мира – непонятно.

Летом 1982 года после восхождения на пики Россия и Коммунизма, экспедиция ЦС ФиС (теперь это Минатом) две недели ждала вертолета на леднике Бивачный (4200 м). Автор продолжил расчеты, и понял, что структура двойственной сети строится с помощью матрицы преобразования А, ортогональной к матрице преобразования токов Крона, матрице С. Крон писал, что он не знает какой физический смысл у матрицы А, но он не знал и двойственных сетях. Таким образом, противоречие, в соответствии с законами диалектики, разрешилось в другой «плоскости», в других измерениях.

Так вот, автор открыл постоянство рассеиваемой мощности в совокупности двух двойственных сетей (цепей). Это физический закон, полученный из расчетов, которые можно рассматривать как мысленные эксперименты. Но это точные расчеты, каждый может проверить – воспроизводимость присутствует, исключений нет. Позднее немало времени было потрачено на то, чтобы расчетам примеров придать теоретическое представление – формулы, математический аппарат, и на сегодня автор готов разговаривать формулами.

Опубликованы, однако, и примеры расчетов разных сетей для подтверждения – раздел 3.2 ТМДС, и другие расчеты, например, в главе 4, коих автор немало включил в эту зеленую книгу, предвидя, что многие будут думать, что здесь просто игра формулами.

Причиной постоянства мощности является фундаментальный закон двойственности структуры – формула (17) в статье, она же на обложке книги ТМДС. С точки зрения философии – двойственный ли инвариант есть следствие закона постоянства мощности (закона сохранения потока энергии), или он сам есть следствие двойственности структуры пространства – в целом это уже дело вкуса. Это такое же равноправие, как активная и пассивная точки зрения на преобразования координат.

Нетер вот законы сохранения импульса, момента импульса, энергии привязала к свойствам однородности, изотропности пространства, и симметрии времени. А здесь появилась структура и двойственность…

Что касается пожелания подтвердить свой вывод (какой?) на основе уравнения полной мощности П.Г.Кузнецова, то зададим вопрос – в какой структуре эта полная мощность (входит, выходит, рассеивается), и как меняется эта структура? И станет ясно, что полной мощности двойственность не мешает, но все потоки и мощности (полезные, вредные, бесполезные) обязаны подчиняться закону двойственности, он же закон сохранения потока энергии. А куда им еще деваться? Все подчиняются, и они тоже…

Таким образом, автор для разрешения противоречия не предлагает свой оригинальный метод, а излагает результаты опытов. Следствием проведенных опытов является обнаруженное (а не придуманное, и не предложенное) свойство двойственности, но это математическая структура, основанная на физической реальности.

Или наоборот, если это вам больше нравится…

В общем – один реализм из опыта, и никакого конструктивизма.

Исследования проведены при поддержке РФФИ, проект №10-06-00486.