Тензорный метод Крона, LT метод Бартини - Кузнецова и двойственные сети

Пространство и время

Сначала было пространство, и было оно пустое и безвидное . Полная пустота. Затем в пространстве появились точки, линии, поверхности, объемы и другие объекты геометрии. Они уже имеют форму, но не имеют материального содержания. И составили они разные и причудливые комбинации структуры, заполнив пространство. Одни геометрические объекты можно выражать через комбинации других геометрических объектов. Так возникают числа, системы координат и базисы. Замкнутые и разомкнутые пути пролегают через точки и линии, а также плоскости и объемы, связывая структуры. Базисы этих путей преобразуются друг в друга с помощью матриц преобразования. Сами пути уже обладают особыми свойствами. Например, разомкнутые, открытые пути нельзя выразить через замкнутые пути

(контуры), а замкнутые пути можно выразить через открытые пути. Пространство обладает свойством двойственности структуры, когда замыканию пути в одном подпространстве, соответствует размыкание пути в двойственном подпространстве, и наоборот. Только вместе двойственные подпространства составляют полное пространство, сохраняющее постоянство открытых и замкнутых путей. Но пространство пока еще пустое. В нем нет времени.

Затем появляется материя. Как? В результате вмешательства, типа большого взрыва, или изначально была, но не рассматривалась, или иным образом. Материя характеризуется массой, веществом и энергией; они взаимно превращаются друг в друга. Пространство само вроде бы не обладало этими свойствами. И вот когда линии и плоскости с объемами наполняются материей (точки образуют границы), а через материю распространяются потоки энергии, то в пространстве возникают процессы. Разные виды материи создают процессы распространения механической, тепловой, электромагнитной, ядерной энергии. Процессы предстают как воздействия источников энергии на материю, в которой возникают отклики, и эти процессы в многообразии своем распространяются в пустом и до этого мертвом пространстве, заполняя его светом энергии и наполняя жизнью. Эти процессы происходят в пространстве, которое изначально обладает свойством двойственности.

Движение требует возникновения времени. Это свойство природы, которое позволяет отличить положение одного и того же (точки, тела, системы) в разных местах пространства. Пока нет времени - точки, плоскости, пути прикреплены к своему положению в пространстве, и неподвижны. Материальные и нематериальные объекты могут находиться везде, в разных местах, ибо нет меры, которая отличает их положение. Время дает меру перемещения вещей в пространстве. Связь пространства и времени создает движение.

Перемещения в пространстве возможны поступательные (прямолинейные) и вращательные, или их комбинация. Здесь проявляется фундаментальное отличие замкнутых и открытых путей. Поступательное движение по открытому пути так удаляет предмет от наблюдателя, что он становится ненаблюдаемым. По этой причине время измеряется с помощью вращательного движения, когда замкнутый путь возвращает предмет наблюдения в исходную точку через определенные промежутки времени.

Процессы и структура

Потом возникли ученые, и стали описывать процессы в одной науке, а структуру связей – в другой науке. Природа не знает о том, что ученые разделили ее на отдельные науки. Процессы описывают уравнениями поведения, которые связывают воздействия на систему и свойства сопротивления ее материи с реакцией системы, т.е. откликами на приложенное воздействие. Например, в электротехнике это ток в ответ на приложенный источник напряжения, или напряжения на ветвях на приложенный источник тока. Структура описывает связи элементов системы, которые создают замкнутые и разомкнутые пути для прохождения потоков энергии. Уравнения для процессов связаны с метрическими пространствами и не содержат структуру. Структуру представляют графами, сетями, симплексами, комплексами, но они не содержат метрики.

Основным достоинством тензорного метода, который разработал Габриель Крон, стало соединение в одном подходе процессов и структуры. По сути Г. Крон, как инженер-электрик, сделал первую попытку связать метрику и структуру, сначала на уровне инженерного расчета и проектирования цепей и электрических машин. Он задавал описание структуры через токи в контурах и пары узлов, на которых возникают напряжения. Для этого он выражал токи в контурах связанной сети через те токи, которые протекали бы в свободных ветвях (включающих в себя источники напряжения или тока).

Коэффициенты такого выражения составляют матрицу преобразования токов, которая обозначается С . В связанной сети независимых контуров меньше, чем в свободных замкнутых ветвях, каждая из которых сама образует контур. По этой причине матрица преобразования токов оказывается прямоугольной.

Откуда взялись тензоры

Тензоры возникли из необходимости описать объекты в пространстве для наблюдателя, которому это надо для того, чтобы сообщить другим наблюдателям. Таким образом, тензоры – это средство создания языка общения наблюдателей. Существует проблема реальности и ее отражения человеком для анализа, исследования и, в конечном счете, развития жизни. Для этого вводят системы отсчета, координат, в которых числа отражают математическую «тень» реальности. При изменении координат меняются числа (компоненты, проекции), но не сама реальность. Хотя сама независимость объекта наблюдения от наблюдателя является одной из проблем измерений.

В математике ввели цилиндрические, сферические, криволинейные системы координат, в которых один объект имеет разные компоненты. Независимые контуры и пары узлов (открытые пути) представляют электрические процессы в цепях. Вращающиеся системы координат связаны с ротором электрической машины. В экономике реальные потоки продуктов и денежных средств отражают в разных системах отчетности (планы счетов, вводимые международные стандарты финансовой отчетности, МСФО и т.д.). Понятию реального, измеримого объекта в математике, по сути, соответствует понятие тензора.

Начиная с середины XIX века, тензоры стали использовать в механике при описании упругих деформаций. Первоначально тензорный анализ называли «абсолютное исчисление». Как составная часть дифференциальной геометрии тензорное исчисление было рассмотрено Г. Риччи и Т. Леви-Чивита. Термин «тензор» ввел В. Фойгт в 1898 г. Г. Крон первым применил тензоры для расчета электрических машин, а затем в электротехнике.

Суть тензорного метода состоит в признании инвариантности объекта в пространстве (вектора, многомерного объема в геометрии; измеримой величины в физике, технике или экономике). Реальный объект существует независимо от субъективных систем координат наблюдателя, в которых объект представлен компонентами (измерен). Если компоненты объекта при изменении системы координат преобразуются по линейным законам (умножением на матрицу преобразования базиса), то это является признаком измеримости объекта и такой объект называется тензором.

В качестве обобщения понятия тензора рассматривается абстрактная система для процессов и структуры одного типа, а конкретные системы рассматриваются как ее «проекции» в координаты, заданные структурой связей. Это позволяет создать обобщенные математические модели и теории в разных предметных областях.

Поток энергии как единая сущность

Применение тензорного метода к исследованию сложных систем началось с электрических машин, которые считались столь сложными системами, что для каждого типа создавалась своя теория (а порой и несколько). «Основателем обобщенной теории электрических машин является Г. Крон, который в 30-х годах предложил уравнения обобщенной машины. В последние десятилетия благодаря применению ЭВМ усилиями многих ученых-электромехаников обобщенная теория электрических машин получила дальнейшее развитие.   …Большинство успехов в теории и практике www.rypravlenie.ru

том 6 №4 (9), 2010, ст. 2.

электромашиностроения связано с математической теорией электрических машин» [2] ( Копылов , 2000, с. 41).

Обобщенная электрическая машина Крона в минимальной форме реализует процесс электромеханического преобразования потока энергии. Другие электрические машины отличаются от обобщенной машины количеством элементов, осуществляющих этот процесс, и количеством связей между ними. Переход от одной машины к другой задает матрица преобразования, которая показывает, как отличаются структуры соединения машин.

В работе «Единая теория электрических машин» [3] ( Kron , 1930) все электрические машины, которые до этого считались несопоставимыми, исследованы с единой точки зрения построения диаграмм , которые показывают величину и направление потоков энергии между различными частями сложной машины. Для этого было применено понятие «свободная энергия» из термодинамики.

Основы тензорной теории электрических машин представлены в статье «Нериманова динамика вращающихся электрических машин» [4] ( Kron , 1934). В 60-тых годах в трудах Японской ассоциации прикладной геометрии данная статья охарактеризована как «сделавшая эпоху». Было введено понятие простейшей (обобщенной) электрической машины из двух элементов – обмоток. Уравнения поведения обобщенной машины Крон получил из уравнений Лагранжа. Тогда уравнения любой машины с другим числом и соединением элементов получаются умножением величин в уравнениях простейшей системы координат (обобщенной машины) на матрицу преобразования C , которая показывает, как соединены обмотки в исследуемой машине. Оказалось, что уравнения электрических машин при стационарном режиме имеют такой же вид, как для неподвижных сетей, при условии, что обычное дифференцирование в уравнении

β dϕα ea Rав i + dt заменяется ковариантным дифференцированием, δ/dt, при котором учитывается изменение вектора при его параллельном переносе вдоль кривой в римановом пространстве:

β δϕ α , ea Rae i + dt где e – напряжение, R – сопротивление (резистанс), i – ток, ϕ – магнитный поток, t – время, а δϕα/dt – ковариантная производная, учитывающая изменение вектора при параллельном переносе в криволинейном римановом пространстве. При малых колебаниях около стационарного вращения – качаниях, это уравнение принимает вид:

5ea = Rae 5ie + Lae ^^dte)- + KSYea i5 iв dx + RaeY ie dxY , где Rαβγ – тензор третьего ранга, определяемый сопротивлениями, а Kδγβα – тензор кривизны Римана – Кристоффеля, наличие которого показывает, что поведение вращающейся электрической машины в режиме качания описывается как движение представляющей точки в неримановом пространстве с асимметричной связью (с кручением).

Форма уравнений для стационарного режима, ускорения и качаний остается одна и та же , но само пространство усложняется за счет все большего искривления. Искривление пространства, представляющего поведение машины, подобно искривлению физического пространства вблизи тяготеющей массы, которое отклоняет луч света (поток фотонов) проходящий мимо поля солнечного тяготения. А. Эйнштейн считал, что Крон распространил в область техники идеи общей теории относительности. Н. Винер отметил, что Крон ввел новый язык, который позволяет не только поставить задачи расчета машин единым образом, но и дать новые методы решения таких задач [11] ( Wiener , 1936).

Инвариант мощности – постоянство потока энергии

Крон исследовал преобразования токов и напряжений при изменении соединения ветвей в цепи. Для этого он ввел понятие простейшей (из отдельных ветвей) сети. Другие сети из данных ветвей являются вариантами соединений ветвей простейшей сети [6] ( Крон , 1978). Для получения уравнений соединенной сети из уравнений простейшей сети использовались матрицы преобразования, которые связывают токи в контурах простейшей сети с токами в контурах соединенной сети (или напряжения на свободных ветвях с напряжениями в разомкнутых путях связанной сети). Они представляют матричную запись законов Кирхгофа.

Крон утверждал, что при соединении ветвей рассеиваемая мощность в электрической цепи не меняется – поскольку остаются прежними источники тока и напряжения, которые задают в сети поток энергии. Это необходимо для получения тензорных формул преобразования напряжения. Постулат об инварианте мощности позволял получить формулу преобразования напряжения. Это ключевой пункт построения тензорного анализа сетей.

Однако известно, что мощность (поток энергии) меняется при изменении связей при изменении структуры . Для заданной цепи состоящей из резисторов и источников, величина напряжения на всех резисторах не выше суммы величин напряжений на источниках. Это следует из теоремы Волавера в теории графов о неусилении мощности в резистивной сети. Суть доказательства в том, что в ориентированном графе каждое ребро находится либо в ориентированном цикле, либо в ориентированном сечении, либо отсутствует в обоих.

Под расчетом цепи понимается вычисление электрических величин или их отношений при заданных схеме и параметрах цепи. В частности, задача состоит в определении откликов в соединенных ветвях при заданных воздействиях в отдельных ветвях. При этом должны выполняться законы Кирхгофа о равенстве нулю суммы токов в каждом узле и равенстве нулю суммы напряжений в каждом контуре.

Суть тензорного метода Крона в электротехнике в том, что к уравнениям процесса прохождения электрического тока добавлено описание структуры связей. Для этого введены матрицы преобразования. Токи i ^a и напряжения e _a на свободных ветвях связаны законом Ома: e _a = z _ae i ^e , где z _ae - матрица комплексных сопротивлений, которая при индуктивном взаимодействии ветвей может и не быть диагональной ( α , β = 1   n ). Если воздействия - источники ЭДС е _а , то откликами являются токи i ^a , для которых уравнения составляют по независимым m контурам. Это система уравнений в матричном виде:

ea' = Z a ' e ' i^e'                                                                      (1)

Для ее решения обращают матрицу комплексных сопротивлений (zap)"¹ = у “^в , тогда:

i ^e ' = (Z a ' e ) " ¹ e a ' = У ^а ' ^в ' e a ' ,                                                          (2)

и по токам в контурах i ^e ' можно определить n токов в ветвях i_c ^в , а затем n напряжений в ветвях e^c_а = z _ae i _c ^в , что является решением задачи цепи.

Если воздействия - источники тока / " , (Крон обозначал в этом случае величины заглавными буквами), то отклики - напряжения E _a , для которых уравнения составляют по независимым парам узлов (базис разомкнутых путей). Система уравнений для j = n -m пар узлов (разности потенциалов отсчитывают относительно базисного узла) в матричном виде:

1 “ = Y “^e Е в- .                                         (3)

Решение этой системы также достигается обращением матрицы:

том 6 №4 (9), 2010, ст. 2.

E e- = 'Г) ^-1 r= Z ae Г' .

Полученные так j напряжений в разомкнутых путях Ев' позволяют определить n напряжений в ветвях Е в , а затем и n токов в ветвях l,"' Y ^в Е в , что является решением задачи цепи. Проверкой является выполнение законов Кирхгофа для найденных токов и напряжений.

Контурный метод и узловой метод расчета цепи Крон представил как преобразования тензоров в пространстве сети, где метрический тензор – сопротивление, а ток и напряжение – контравариантные и ковариантные векторы. В основе метода преобразование токов при соединении ветвей в сеть. Коэффициенты выражения токов в n свободных ветвях i ^a через токи в m контурах связанной сети i ^a '

составят матрицу ^mC ^a _a (порядка m x n ):

i

^mC ^aa ' i ^a ' .

Строки матрицы mC показывают, в какие контуры входит данная ветвь, а столбцы - из каких ветвей состоит контур. Рассеиваемая мощность P равна сумме мощностей на ветвях, т.е. произведений напряжения и тока в каждой свободной ветви: P = ea ia.

Аналогично для напряжений и токов в контурах связанной сети:

P' = e a ' i ^a ' ,

где предполагается сумма по одинаковым верхним и нижним индексам. Если постулировать, что мощность при изменении соединений не меняется, и подставить (5), то получим закон преобразования для напряжения, ea- ia' = ea ia = ea Caa- ia', откуда:

e a- = e a ^m C ^a_a- = ^m C ^a_a-_t e a ,                                     (7)

где индекс t означает транспонирование матрицы. Чтобы получить формулу преобразования z _ae , подставим (5) и (7) в (6):

e a = Z ae i ^e = Z ae m C^ Г ,                               (8)

но для этого надо в (7) получить обратное преобразование e _a = (ⁿC ^a _a-_t)"¹ e_a- . Это возможно когда сеть состоит из одних контуров; в этом случае матрица C^a_a- квадратная, и может иметь обратную матрицу. В общем случае, когда число контуров меньше числа ветвей, это невозможно, поскольку матрица ^mC ^a _a ' прямоугольная, для нее не существует обратной матрицы. Однако если формально подставить в (8), то:

e a = («" „ ) ea- = Z ae " Г\ _; i ^a ' ,                               (9)

том 6 №4 (9), 2010, ст. 2.

а затем умножить обе части уравнения на матрицу (C^a_a-)_t то получим:

( ” C ^aa ) t ( m C -a- t )¹ C a ' = (CCa) t Z ae ’ С^) - ¹ ^ = C a ,                      (10)

откуда, используя постулат о том, что вид уравнений поведения не меняется при соединениях [6] ( Крон , 1978), получим формулу преобразования импеданса:

Z a-в' = ( " C ^aa' ) t Z ae C .                                           (11)

В этой формуле нет обратных матриц преобразования, а значит и не надо «обращать» прямоугольные матрицы. Далее расчет производится контурным методом. Если подставить все формулы преобразования в выражение токов в ветвях связанной сети, то получим:

i c ^в = ” C ”a - ( " C ",; Z ae '«"„Г ’ C ^-,; C „ = ” Y_C e a

Матрицу ^mY_c , которая выражает токи в ветвях связанной сети через заданные источники ЭДС, назовем «матрицей решения».

Делая двойственные замены величин, получим формулы расчета цепи узловым методом, при этом матрица C заменяется на ортогональную матрицу А = C¹_t. Крон полагал, что матрица А не имеет такого структурного смысла, как матрица С . Автор показал, что матрица А является также матрицей преобразования С = А в двойственной цепи (сети).

Обосновать постулат об инварианте мощности пытались физики, например, Б. Гофман, и математики, Дж. Рот. Дискуссия по применению тензоров в технике растянулась на десятки лет. Эти обсуждения, в том числе на страницах журнала «Электричество», носили, как отмечал автор, острый характер, порой выходя за рамки научной терминологии [7] ( Петров , 1985). Одни применяли тензорный метод в различных областях физики и техники. Другие отвергали его за прямоугольные матрицы, которые не образуют группу. Несмотря на проблемы, «эти работы, несомненно, оказали глубокое влияние на развитие многих областей знания и способствовали прогрессу в разработке методов решения системных задач с помощью цифровых вычислительных машин» [1] ( Веников, 1985).

Аналогии предметной области и модели

Крон писал, что чем дальше он уходил от электротехники, к сетевым моделям в физике, технике, тем более точно пришлось определять основные понятия в самой электротехнике. Сегодня можно сказать, что здесь проявились общие законы структуры, которые присущи всем неживым и живым системам, от микромира до космических масштабов. Крон создал целый ряд сетевых моделей в виде электрических цепей. Цепи были его языком моделирования, матрицы преобразования Крона выражают базисные токи в связанной цепи, через токи в свободных ветвях. Позднее он признавал, что замкнутые и разомкнутые пути в сети – это более абстрактные средства для представления потоков энергии, чем физические величины тока и напряжения.

Крон моделировал эквивалентными цепями технические, физические систем, которые имели аналогии процессов и структуры. Были построены модели в виде эквивалентных электрических цепей для уравнений поля Максвелла ( Kron , 1944), Шредингера ( Kron , 1945), Навье-Стокса, модели упругих систем (строительные конструкции, разрезные диафрагмы турбин), модели электронных ламп, электрических машин, сетей передачи электроэнергии, ядерного реактора, транспортной задачи и другие. Эти модели представлены в Диакоптике ( Крон , 1972), как основа алгоритмов для расчета сложных систем по частям.

До появления ЭВМ Крон в 40-е годы применял физические реализации моделей как аналоговые машины для решения задач, например, распространения электромагнитных волн в полых резонаторах ( Carter, Kron , 1944, 1945). С появлением цифровых ЭВМ матричное представление задач и структуры систем применялось для расчета эквивалентных моделей предметных областей ( Крон , 1972). С развитием ЭВМ с параллельной архитектурой расчет сетей по частям стал одним из методов организации (на уровне математической модели) параллельных вычислений ( Петров , 1991), в том числе для транспьютеров ( Bowden K ., 1988, 1989). Расчет больших цепей на сети транспьютеров с помощью диакоптики в параллельной форме рассматривали Фуско и Меругу ( Fusco V. F., Merugu L.N., 1991).

В перспективе представляют интерес работы Крона по многомерным (полиэдральным) сетям. Полиэдральные сети, рассмотренные в статьях 1958–1968 гг., состоят не только из одномерных ветвей, но также из плоскостей, точек, объемов, многомерных элементов; и проводят не только электрический ток, но и потоки энергии других видов. Например, магнитные и диэлектрические силовые линии определяются через поверхностные интегралы по некоторым плоскостям графа, ограниченным контурами. Магнитный поток распространяется через двумерные поверхности (представлены обмотками в электрической машине). Таким образом, электромеханические преобразователи (электрические машины) являются простейшим примером полиэдральных сетей, в данном случае двумерных сетей.

Совокупность сетей из точек, отрезков, плоскостей и т.д., или 0-, 1-, 2- и т.д. – до n-мерных симплексов, при возбуждении электромагнитными волнами Крон назвал волновым автоматом. Он применял такой волновой автомат в качестве многомерного пространственного фильтра, для проведения многомерных кривых по экспериментальным данным методом наименьших квадратов в регрессионном анализе ( Kron , 1962). Двойственными к p-сетям рассматриваются (n – p)-сети в n-мерном пространстве ( Kron , 1965). Крон утверждал, что полиэдральные волновые автоматы обладают свойствами самоорганизации в смысле изменения их параметров их состояния в ответ на внешние воздействия. Воспроизвести режим самоорганизации полиэдральной сети последователям Крона в дальнейшем не удалось, хотя в Англии Дж. Линн повторил расчеты Крона с помощью волнового автомата.

LT метод Бартини-Кузнецова

Важнейшим элементом моделирования являются аналогии между предметной областью и сетевой моделью. Аналогии между структурой путей, связанных элементов распространения потоков энергии достаточно наглядны и понятны. Сложнее понять аналогии между воздействиями и откликами механической, гидравлической, тепловой, электромагнитной, экономической системы и величинами сети. Что же позволяет их сопоставить и сравнить? В чем аналогии измерения столь различных измеримых величин?

Существует немало систем измерения физических величин, которые выбирают тот или иной набор величин в качестве базисной основы. Остальные физические величины определяются через базисные величины. Это позволяет сопоставлять физические величины, которые относятся к разным предметным областям, с помощью анализа размерностей. Понятие размерности ввел в физику Фурье в 1822 году.

Принятым на сегодня в большинстве стран стандартом является международная система единиц измерения СИ. СИ определяет семь основных и производные единицы физических величин: килограмм, метр, секунда, ампер, кельвин, моль и кандела. В рамках СИ считается, что эти единицы имеют независимую размерность, т. е. ни одна из основных единиц не может быть получена из других.

Вместе с тем классики утверждают, что в мире нет ничего, кроме материи, которая движется в пространстве и времени. Следовательно, можно ожидать, что существует такая система измерения, в которой все физические величины выражаются через две наиболее фундаментальные – пространство (протяженность) и время (длительность).

Возможность выразить все физические величины через длину и время отмечал Максвелл ( Максвелл , 1954), а затем Кельвин, Эддингтон и другие. Разработал такую систему Б. Браун ( Brown , 1941) и независимо от него в 1966 году Р.Л. Бартини ( Бартини , 1965, Бартини , 1966). Система представлена таблицей, в клетках которой расположены физические величины соответствующей размерности по длине и времени. Фрагмент таблицы LT для размерностей физических величин ( Бартини, Кузнецов , 1974; Большаков , 2002) представлен на рисунке. Вместе с тем П.Г. Кузнецов показал, что клетки физических величин соответствуют определенным типам геометрии, и различным видам физической теории. Каждой физической величине соответствует своя геометрия.

Время, T-1 (сек.)-1

						L3 T-6	L4 T-6	Изменение мощности	Скорость передачи мощности
T-5				L1 T-5	Изменение давления L2 T-5	Поверхностная мощностьL 3 T-5	Скорость изменения силы L4 T-5	Мощность L5 T-5	Скорость передачи энергии
T-4				Изменение плотности тока L1 T-4	Давление L2 T-4	Поверхн. натяжение L3 T-4	Сила L4 T-4	Момент силы Энергия L5 T-4	Скорость передачи действия
T-3		Гидравлич. сопротивле ние L-1 T-3	Изменение углового ускорения T-3	Скорость массы Плотность тока L1T-3	Напряжен. электро-магн. поля Вязкость L2 T-3	Ток Массовый расход L3 T-3	Скорость смещения заряда Импульс L4 T-3	Момент импульса Действие L5T-3	Момент действия
T-2		Изменение объемной плотности	Массовая плотность Угловое ускорение T-2	Линейное ускорение L1T-2	Напряжение (разность потенциалов) L2 T-2	Масса , Колич-во магнетизма Заряд L3 T-2	Магнитный 4 момент L T-2	Момент инерции L5 T-2
T-1		L-1 T-1	Частота T-1	Скорость Электрич. сопротивл. L1 T-1	Скорость изменения площади L2T-1	Скорость изменения объема L3T- 1	Скорость смещения объема L4 T-1	L5 T-1
T0		Изменение проводимо сти	Безразмерные константы	Длина Емкость Самоиндукция L	Площадь L2	Объем L3	4-Объем L4	5-Объем L5
T1	Изменение магнитной проницаемости	Электрич. проводимость L-1 T1	Период	Длительность расстояния	L2T1
T2	Магнитная проницаемость	L-1 T2	Поверхность времени	L 1 T2
T3	L-2 T3 Текучесть	L-1 T3	Объем времени	Гидравлич. проводим. L 1 T3
	L-2	L-1	L 0	L 1	L 2	L 3	L 4	L 5	L 6

Длина L, м

Рис. 1. LT-таблица размерностей физических величин Бартини-Кузнецова

Выражение величин в данной таблице через длину и время неявно предполагает тождество гравитационной и инерционной массы. «В принципе ниоткуда не следует, что масса, создающая поле тяготения, определяет и инерцию того же тела. Однако опыт показал, что инертная и гравитационная массы пропорциональны друг другу (а при обычном выборе единиц измерения численно равны). Этот фундаментальный закон природы называется принципом эквивалентности. Экспериментально принцип эквивалентности установлен с очень большой точностью» (ФЭС, с 393). Существование самой LT таблицы можно считать важным теоретическим аргументом в пользу данного принципа.

Принцип эквивалентности позволяет приравнять силу в уравнениях закона гравитации F = т²/Г и второго закона Ньютона F = m а. Тогда m = Г а. Обозначая длину L , а время T , и учитывая, что размерность обозначают квадратными скобками, получим, что [ r² ] = L² , а размерность ускорения [ a ] = L 1 T² . Отсюда размерность массы получим: [ m ] = L3 К² , т.е. она выражена через длину и время. Аналогично можно выразить электрический заряд и количество магнетизма, которые попадают в ту же клетку таблицы, что и масса. Например, количество движения (импульс), величина векторная, т.е. имеющая направление, имеет размерность в терминах пространства и времени как произведение массы и скорости

[ p ] = [ m ] [ v ] = L ³ T"² L ¹ T 1 = L 4 T •

Клетки таблицы физических величин на рисунке содержат величины с одинаковой физической размерностью, выраженной через пространство (длину) L и время T . Каждую такую величину следует рассматривать как инвариант, постоянство которого относительно определенной группы преобразований соответствует физической теории или закону. Как известно, различные виды геометрии отличаются инвариантами и сохраняющими их группами преобразований. Например, группе преобразований, сохраняющих длину, соответствует физика движения твердого тела. Группе преобразований, сохраняющих объем, соответствует физика движения несжимаемой жидкости, и т.д.

Уравнение инварианта. В каждой предметной области произведение соответствующих пар продольных и поперечных величин имеет физическую размерность мощности (потока энергии). В терминах таблицы Бартини-Кузнецова это [ L5 Т5 ]. Например, электрические ток и напряжение; в механике сила в точке и скорость (как разность положения тела в двух точках в единицу времени); в

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление» www.rypravlenie.ru том 6 №4 (9), 2010, ст. 2.

гидродинамике поток жидкости (объем в единицу времени) и давление; в термодинамике поток тепла и температура; поток массы и концентрация (химический потенциал) и т.д. Распределение размерностей в каждой паре различное, но произведение величин имеет размерность [ L 5 Т 5 ]. Например, ток имеет размерность [ 1; Т3 ], а напряжение - [ L2 К² ]; давление - [ L² К⁴ ], а поток жидкости (скорость изменения объема) - [ L 3 Т¹ ]; сила - [ L⁴ Т ⁴ ], а скорость - [ L 1 Т¹ ] и т.д. Образно говоря, если мир сложен из одинаковых кирпичей потока энергии, то в разных предметных областях эти кирпичи состоят из разных блоков. Это обстоятельство и дает основу для установления аналогий между величинами процессов при создании сетевых моделей предметных областей с помощью LT метода Бартини-Кузнецова.

Для создания сетевых моделей не меньшую роль играет структура. Сложные системы отличаются наличием большого количества элементов, соединение элементов образует структуру. Структуру трудно считать материей. Ее значение нельзя измерить приборами так, как это делается с физическими величинами. Понятиям структуры (симплексы, комплексы, замкнутые и разомкнутые пути) нет места в системе измерения физических величин, например в LT таблице Бартини-Кузнецова. Вместе с тем понятие структуры пронизывает все, что существует, как живые, так и неживые системы, на всех уровнях от масштабов микромира до космических масштабов.

Инвариант мощности и двойственные сети

Таким образом, реально постулат Крона об инварианте мощности не выполняется, поскольку мощность при изменении связей меняется, а вывод формул тензорного анализа сетей содержит недопустимое обращение прямоугольной матрицы. Однако его метод расчета цепей и машин дает правильные результаты. Получается диалектическое противоречие. Автор исследовал изменение мощности в цепи при изменении структуры, чтобы найти закон. Оказалось, что решение, в согласии с диалектикой, лежит в другой «плоскости». Рассеиваемая мощность меняется в одной цепи при изменении связей, но постоянна в сумме двух цепей: рассматриваемой цепи и цепи с двойственной структурой.

Фундаментальное свойство двойственности структуры выражает закон, который связывает матрицы преобразования цепей с двойственной структурой. Математически этот закон представляет собой постоянство метрических тензоров структуры в данном подпространстве и двойственном подпространстве. Это свойство двойственности самого пространства. По своей сути инвариант двойственности является причиной того, что существует закон сохранения потока энергии. Этот закон сохранения, следующий по физической размерности после закона сохранения энергии, является физико-структурным законом. Можно рассматривать закон сохранения потока энергии как причину существования свойства двойственности пространства. Тогда из него следует существование двойственных структур, расположенных в двойственном пространстве.

В сети двойственными являются замкнутые и разомкнутые пути, воздействия и отклики, сеть и двойственная к ней сеть (ее величины подчеркнуты). Если, например, соединить две ветви, то два узла сливаются (уменьшается число узлов). Тогда возникает новый независимый контур, увеличивается размерность подпространства замкнутых путей. При этом исчезает разомкнутый путь, уменьшается размерность базиса разомкнутых путей. Общая размерность пространства путей сети не меняется, она постоянна и равна количеству элементов – ветвей, т.е. n = m + j .

В двойственных сетях постоянны размерности дополняющих друг друга подпространств замкнутых и разомкнутых путей. Каждому замкнутому пути в сети соответствует разомкнутый путь в двойственной сети, и наоборот. Слиянию двух узлов в сети соответствует разделение узла на два в двойственной сети, и наоборот. Таким образом, для двойственных сетей при изменении структуры общая размерность подпространств замкнутых путей постоянная; общая размерность подпространств разомкнутых путей постоянная. Свойства изменения структуры двойственных сетей показаны в таблице 1.

Табл. 1. Соответствие преобразований структуры двойственных сетей

	Сеть	Двойственная сеть
Тип соединения ветвей	параллельное	последовательное
Ориентация ветвей	встречная	согласованная
Преобразование структуры	Слияние узлов	Разделение узлов
– изменение соединений	J’ = J – 1	J ’ = J + 1
• изменение контуров	возникает контур m’ = m + 1	исчезает контур m ’ = m – 1
•   изменение открытых путей	исчезает разомкнутый путь j = j’ + 1	возникает разомкнутый путь j = j’ – 1

Для двойственных сетей существуют инварианты. Сумма метрических тензоров постоянна. Сумма токов в каждой ветви постоянная. Сумма напряжений на каждой ветви постоянная. Сумма мощностей, рассеиваемых в двойственных сетях постоянная.

Все величины, относящиеся к двойственной сети, обозначим подчеркиванием. Число ветвей в сети и двойственной сети одинаковое, т.е. каждой ветви в сети соответствует ветвь в двойственной сети. Каждому замкнутому пути в сети соответствует разомкнутый путь в двойственной сети, а каждому разомкнутому пути в сети соответствует замкнутый путь в двойственной сети. Таким образом, n = n, m + m = n, j + j = n.

Сеть и двойственная сеть дополняют друг друга. Подпространства контуров и подпространства разомкнутых путей двойственных сетей в сумме имеют размерность полного пространства сети. Таким образом, двойственные сети обладают полнотой единого объекта в пространстве.

Свойства двойственности присущи самой структуре, даже без материи. Например, если сопротивления ветвей равны единицам ( Z = Y = I ), то инвариант двойственности связывает матрицу решения сети и матрицу решения двойственной сети:

^mC (^mC t ^mC)^{-1 m}C t + ^jA (^jA t ^jA)^{-1 j}A t = ^mC (^mC t ^mC)^{-1 m}C t + ^m C (^m C t ^m C )^{-1 m} C t = I,   (12)

где ^mC = ^j A – матрица преобразования замкнутых путей сети, или разомкнутых путей двойственной сети, а ^jA = ^m C – матрица преобразования разомкнутых путей сети, или замкнутых путей двойственной сети, I – единичная матрица. Слагаемые в данном соотношении представляют собой метрические тензоры соответствующих двойственных сетей, ветви которых имеют единичные веса. Это означает, что воздействие и отклик в таких ветвях численно равны друг другу, они не оказывают сопротивления материи прохождению потока энергии. Это закон структуры, не связанный с материей. Сюда входят только матрицы преобразования путей.

Если ветви сети имеют веса-сопротивления (собственные и взаимные), выражаемые матрицей сопротивлений, метрического тензора Z ≠ I , ( Z = Y^-1 ), то инвариант двойственных сетей для замкнутых путей примет вид:

^mC (^mC t Z ^mC)^{-1 m}C t + Y ^m C (^m C t Y ^m C )^{-1 m} C t Y = Y = (Z) ^-1 ,                         (13)

Для разомкнутых путей инвариант имеет двойственный вид, с заменой С на А, Z на Y. Инвариант связывает метрические тензоры двойственных сетей. Если в сети есть воздействие, то его компоненты расположены в базисе замкнутых (внутреннее воздействие) или разомкнутых (внешнее воздействие) путей. В данном случае инвариант – это постоянство квадрата величины вектора: часть вектора расположена в www.rypravlenie.ru

том 6 №4 (9), 2010, ст. 2.

сети, часть в двойственной сети, но их сумма постоянна и не зависит от изменения соединений. Для вектора ^m d , например, заданного в замкнутых путях, формула преобразования контравариантных компонент при изменении структуры, полученная на основе инварианта двойственных сетей, имеет вид:

m α d ₀

m d ^ + m d ^ = m d° C-° + m d° A - 'Y ^ep = (X- ^a ) t m d° + ( j^' ) _tY ^ep m d ^в , (14)

где md0α – компоненты вектора в свободных ветвях, а mdcα и mdcα – компоненты вектора в связанных двойственных сетях. Нельзя непосредственно получить компоненты вектора md , для связанной сети по их значениям в свободных ветвях, поскольку в связанных ветвях они распадаются на совокупность компонент вектора в двойственных сетях и только в сумме дают компоненты полного вектора.

С точки зрения физики «вектор» можно рассматривать как совокупность источников напряжения, ЭДС (в базисе контуров), или как совокупность источников тока (в базисе открытых путей).

Поток энергии, численно равный мощности, рассеиваемой в сети, можно наглядно представить круговой диаграммой как красно-синий детский «мячик», до половины погруженный в «воду». Получается, что двойственная сеть должна располагаться в некотором двойственном пространстве, «параллельном» наблюдаемому нами пространству.

Площадь темной (красной) половины такого мячика соответствует мощности (или квадрату величины вектора) в замкнутых путях как данной, так и двойственной сети, а площадь светлой (синей) половины – мощности в разомкнутых путях. При изменении структуры мощность в двойственных цепях меняется. Это можно представить пропорциональным изменением площадей разных цветов при вращении двухцветного мячика, между границами наблюдаемого и ненаблюдаемого пространства, где:

• •    «воздушная» среда представляет наблюдаемое пространство,

• •    «водная» среда представляет двойственное пространство.

Вращение «мячика», представляющего собой диаграмму изменения мощности, меняет доли красного и синего цвета над (и под) поверхностью раздела двух сред. Сумма площади красного цвета (мощность внутренних источников, т.е. источников напряжения, ЭДС) над и под поверхностью (в данной и двойственной цепи) постоянна – соотношение (12). Сумма площади синего цвета (мощность внешних источников, т.е.

тока) над и под поверхностью постоянна (13). Сумма площади красного и синего цвета над поверхностью, а также сумма площади красного и синего цвета под поверхностью, постоянны. При изменении структуры двойственных цепей, рассеиваемая мощность, меняется, но согласованно, так, что остаются постоянными четыре суммы в базисах замкнутых путей и разомкнутых путей. Эти суммы можно разделить на инварианты в пределах одной цепи, т.е. инвариант «по горизонтали диаграммы» и на инварианты в двух двойственных цепях, т.е. инвариант «по вертикали диаграммы», а именно:

• •    инварианты «по вертикали диаграммы»:

o базис замкнутых путей – внутреннее (контурное) возбуждение, данная сеть и двойственная сеть (темная половина), замкнутые сети;

o  базис разомкнутых путей – внешнее (узловое) возбуждение, данная сеть и двойственная сеть (светлая половина), открытые сети;

• •    инварианты «по горизонтали диаграммы»:

• o    данная сеть, контурное возбуждение и узловое возбуждение (верхняя половина);

• o    двойственная сеть, узловое и контурное возбуждение (нижняя половина).

Постоянство суммарной рассеиваемой мощности при изменении структуры двух двойственных цепей – это проявление закона сохранения потока энергии. Полная диаграмма изменения мощности при изменении структуры данной и двойственной сетей, в которых заданы источники энергии двух типов, представлена на рисунке 2.

том 6 №4 (9), 2010, ст. 2.

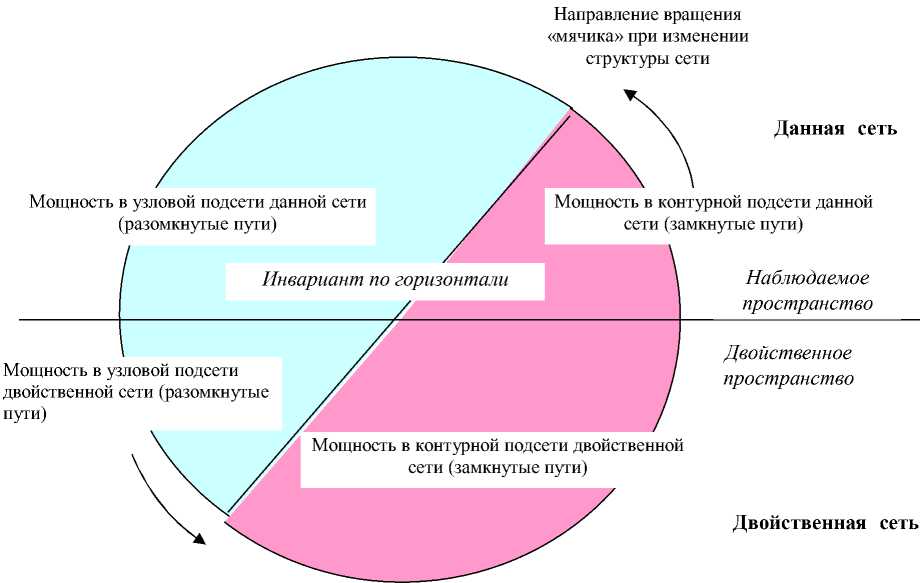
Рис. 2. Диаграмма изменения мощности в двойственных цепях при изменении структуры

Рассмотрим подробнее виды инварианта мощности. Как отмечалось, диаграмма показывает два вида двойственности сетей и инварианта мощности. Для каждого из них инвариантом является площадь полукруга, представляющая два вида мощности. Один вид инварианта – «по вертикали», т.е. потоку энергии соответствует один вид путей, один вид источника, но две сети. Мощность постоянна в двух двойственных сетях при изменении структуры, как для замкнутых путей, так и для разомкнутых путей. Соответственно, для внутренних источников (напряжения) замкнутых систем и для внешних источников (тока) открытых систем. Здесь работает двойственность структуры двух цепей (сетей).

Другой вид инварианта – «по горизонтали», т.е. потоку энергии соответствуют два вида путей, два вида источников, но одна сеть. Это постоянство рассеиваемой мощности в одной сети (цепи) в сумме от внутренних источников и внешних источников. Это при условии, что мощности источников в каждой ветви равны друг другу, либо равны нулю. Если источники тока и напряжения в ветви не равны друг другу, то рассеиваемые от них мощности все равно подчиняются инварианту двойственных сетей, хотя соответствующая диаграмма не будет столь наглядной. Здесь работает двойственность замкнутых и разомкнутых путей в структуре одной цепи.

Двойственное пространство располагается (существует) «параллельно» в любой точке наблюдаемого пространства и участвует в преобразовании потоков энергии при их движении по путям, создаваемым структурой. По своей сути двойственные пространства в совокупности составляют единое пространство. Таким образом, параллельное пространство располагается вокруг нас, оно должно контактировать с объектами, расположенными в «нашем», наблюдаемом пространстве, при распространении потоков энергии, проявляя себя при изменении структуры систем, по которым энергия распространяется.

Исследования проведены при поддержке РФФИ, проект 10-06-00486.