Тензорный метод расчета систем с переменной структурой

Сложные технические и экономические системы состоят из процессов в элементах и структуры связей этих элементов. Управление такими системами требует расчета изменения процессов при изменении структуры связей, включая разделение на части и расчет по частям. Диакоптика Крона как метод исследования сложных систем по частям ограничена двумя видами сетевых моделей – диффузионного и пуассоновского типа [1]. Тензорный метод двойственных сетей обобщает расчет сетевых моделей при любых видах изменения структуры. В основе метода инвариант двойственности – постоянство суммы метрических тензоров (матриц решения) двух сетей с двойственной структурой. В физике этому соответствует постоянство суммы рассеиваемых мощностей (потока энергии) двух электрических цепей при изменении их структуры [2, 3]. Известно (по теореме Э.Нетер), что изотропность и однородность пространства, а также однородность времени соответствуют законам сохранения момента импульса, количества движения и энергии. Сохранению потока энергии соответствует двойственность пространства. Задача состоит в расчете изменения процессов в сетевой модели сложной системы при изменении структуры связей.

Диакоптика

Пионер диакоптики Г. Крон считал главной целью расчет силы связей разделенных частей для решения целой системы. Вместе с тем необходимо управлять поведением больших систем при различных изменениях структуры, не только при расчленении на части, но и при изменении соединений элементов или подсистем. Например, для расчета вариантов конструкции проектируемой системы, или анализ поведения системы при отключении, разрушении частей. Или для выбора структуры системы с заданными свойствами.

Термин «диакоптика» образован от греческого «копто», означающего «разделять на части» и приставки «диа», усиливающей слово, стоящее за ней, т.е. разделение на части как систематический метод [1, с. 14]. Диакоптика включает в себя создание сетевой модели исследуемой системы с использованием аналогий процессов и структуры, расчет модели при изменениях структуры, включая расчет по частям, использование результатов для проектирования, анализа, управления системой.

Преобразования путей при изменении структуры

Сети состоят из ветвей – направленных отрезков с границами-узлами. Если ветвь замкнута, то ее границы сливаются в один узел. Ветвь определяет измерение в пространстве сети. Ветви соединяются узлами. Слияние или разделение узлов изменяет структуру сети.

Координатами в пространстве сети являются пути. Путь проходит по ветви, направления ветви и пути могут совпадать. В замкнутой ветви путь замкнутый, в разомкнутой ветви – разомкнутый. Путь может проходить по нескольким ветвям: по одной ветви от начала до конца, затем переходит к другой ветви, и т.д. Замкнутый путь возвращается в начало, иначе это разомкнутый путь. В сети с потоками путь составляет непрерывную линию без разветвлений. Пути заданы составляющими их ветвями с учетом взаимной ориентации.

Базис замкнутых путей должен охватить все ветви. Базис разомкнутых путей должен охватить все узлы сети. Размерности подпространств замкнутых и разомкнутых путей определяют известные топологические соотношения.

• (1)    j = J – s ,

• (2)    n = m + j.

где n - количество ветвей в сети, J - количество узлов, s - подсетей, m - независимых замкнутых путей, j - независимых разомкнутых путей.

Пути в новой сети выражают через пути в старой сети, комбинируя составляющие их ветви с учетом ориентации. Это позволяет описать изменение структуры. Коэффициенты выражения путей составляют матрицу преобразования С . Удобно использовать матрицу перехода от несоединенных, свободных ветвей к связанной сети.

Подпространства замкнутых и разомкнутых путей независимы, но вместе образуют пространство сети. Независимость выражается ортогональностью матриц преобразования путей при изменении структуры [3]. Изменение соединений ветвей одни пути замыкает, а другие пути размыкает, что меняет размерность их подпространств. Матрицы преобразования становятся прямоугольными, не образуют группу, как преобразования координат в обычном пространстве. Это создавало трудности обоснования тензорного метода расчета сетей и сетевых моделей при изменении структуры.

Оказалось, что сети обладают свойством двойственности, которое связывает преобразования структуры [2, 3]. Ветвь состоит из замкнутой и разомкнутой частей. При соединении ветвей возникают две сети с двойственной структурой. Двойственные сети составляют полное пространство структуры. Размыканию пути в одной сети соответствует замыкание пути в двойственной сети, и наоборот.

Пусть замкнутые свободные ветви – сеть, а свободные разомкнутые ветви – двойственная сеть. Суммы базисных замкнутых и разомкнутых путей в двух двойственных сетях остаются постоянными и равны числу ветвей (или путей в простейшей сети) при любой структуре связей ветвей.

• (3)    n = m = m' + j' = j'+ m' = m' + m' = j' + j' = j = n.

Величины в связанной сети даны со штрихами, а в двойственной сети подчеркнуты.

Матрица преобразования путей С заданной сети показывает, из каких ветвей состоит каждый путь базиса. Ортогональная матрица преобразования А = С Ч показывает, из каких ветвей состоят пути двойственной сети. Пример двойственных сетей и матриц преобразования для одного из вариантов выбора путей представлен на рисунке.

том 14 № 4 (41), 2018, ст. 1

Данная сеть

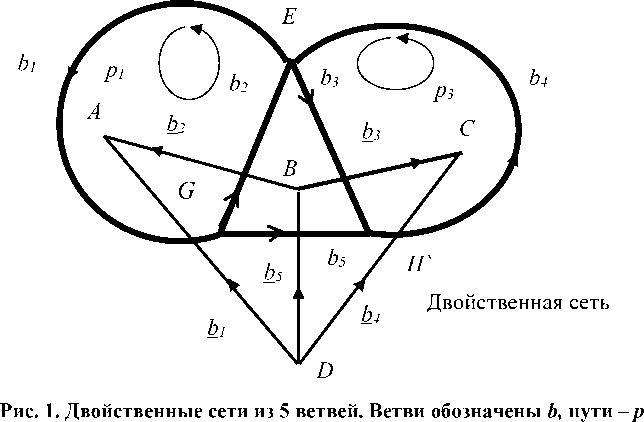
Этим сетям соответствуют матрицы преобразования путей старого базиса свободных ветвей в новый базис путей в связанных ветвях. Матрица преобразования C заданной сети (жирные линии) и матрица преобразования С = А = С-1t двойственной сети (тонкие линии).

p 1

p 2

p 3

p 4

p 5

p 1

p 2

p 3

p 4

p 5

p 1 `

1

1

m

p 1 `

1

j

p 2 `

1

1

–1

m

p 2 `

–1

1

j

p 3 `

1

1

m

p 3 `

1

–1

1

j

С = А = p 4 `

1

j

С = А = p 4 `

–1

1

–1

1

m

p 5 `

1

j

p 5 `

–1

1

1

m

m

m

m

j

j

j

j

j

m

m

Матрицы преобразования С и А состоят из подматриц замкнутых путей ^mC = ^j A и разомкнутых путей ^jA = ^m C . Матрицы преобразования имеют нулевой блок выражения разомкнутых путей через замкнутые пути . Разомкнутый путь нельзя выразить через замкнутые пути потому, что они охватывают часть плоскости, т.е. вводят новое измерение. Замкнутые одномерные пути создают разомкнутые двумерные пути в сети из двумерных элементов.

Сеть рассматривается как тензор, а разные структуры соединения ее ветвей – как проекции в системы координат. Форма уравнений поведения не зависит от структуры. При изменении структуры сети, ее пути, векторы, другие величины преобразуются с помощью матрицы преобразования путей подобно тензорам при изменении системы координат.

Воздействующий на сеть внешний вектор представлен компонентами в разомкнутых путях, а внутренний вектор – в замкнутых путях. Контравариантные компоненты представлены в прямом базисе путей, а ковариантные компоненты представлены во взаимном базисе. Взаимный базис задан парой поверхностей с ориентаций, фиксирующей их порядок. В электрической цепи этому соответствуют эквипотенциальные поверхности, которые определяют разность потенциалов на открытых путях (парах узлов).

Метрический тензор в пространстве сети описывает веса ветвей, составляющих пути. Матрицу метрического тензора сети для замкнутых путей обозначим Z , а для разомкнутых путей Y ( Z = Y"¹ ). Матрица Z сети показывает , сколько ветвей, и с какими весами входит в состав базисного пути, какие ветви являются общими для разных путей базиса, с учетом их взаимной ориентации. Матрица Y показывает то же самое для двойственной сети.

Существует инвариант изменения структуры: сумма метрических тензоров двух двойственных сетей при любой структуре постоянна и равна метрическому тензору свободных ветвей. Если веса ветвей равны единице, то инвариант описывает свойства структуры (без материи, или потоков энергии), и выражается только через матрицы преобразования контурной и узловой сетей, или двойственных сетей [2, 3, 4]:

• (4)....... m C t ( m C m C t )¹ m C + A (A j A ) ^jA = m C t ( m C m C t )¹ m C + ^mC_t ( m C m C t )¹ m C = I.

где I - единичная матрица.

Если веса (метрика) ветвей не равны единице, и представлены матрицей метрического тензора Z +1 , то инвариант двойственности для замкнутых путей принимает вид:

• (5)....... m C ( m C t Z m C)^{-1 m}C_t + Y m C ( m C t YmQ^-1 m C t Y = Y = (Z)^-1.

Двойственность величин, характеризующих сеть, позволяет получить этот инвариант для разомкнутых путей при замене С на А , Z на Y .

Расчет сетей тензорным методом

Поведение сети описывает уравнение закона Ома e = Z i , где e вектор источников воздействия (например, ЭДС), Z - метрический тензор (матрица сопротивлений), а i - вектор откликов (токи в ветвях). Решением для простейшей сети из свободных замкнутых ветвей является i = Z"¹ e , где отклики в ветвях выражены через воздействие и метрику.

При связывании свободных замкнутых ветвей в сеть, часть контуров размыкается. Выражение новых путей через старые пути описывает прямоугольная матрица ^mC , поскольку в связанной сети независимых контуров в общем случае меньше, чем в свободных ветвях. Расчет измеримых токов i c в ветвях соединенной сети по воздействиям e в простейшей сети производится контурным методом как преобразование координат [2, 3]:

• (6)             i c = ^mC_t ( m C Z m C t )^- m C e = Y c e

Здесь Y c есть метрический тензор связанной контурной сети, или матрица решения, умножение которой на вектор источников e позволяет сразу получить токи i c в ветвях.

Поведение простейшей сети из свободных разомкнутых ветвей также описывает уравнение закона Ома I = Y E , где I вектор внешних воздействий (например, источников тока), Y – метрический тензор (матрица проводимостей), а E – вектор откликов (напряжения на ветвях). Решением в данном случае является E =Y^-1 I , где отклики в ветвях выражены через воздействие и обратную метрическую матрицу.

При связывании свободных ветвей в сеть, часть разомкнутых путей замыкается. Это преобразование описывает матрица ^jA . Метрический тензор разомкнутых путей определяет поведение сети при внешних воздействиях, которые входят в сеть в одном узле, а покидают в другом узле. В электрической цепи этому соответствует узловой метод расчета, где воздействием являются источники тока, а отклики суть напряжения (разности потенциалов) на ветвях, связанные проводимостью.

• (7)    E c = ^jA t (^jA Y ^jA t )^{-1 j}A I = Z c I

Здесь Z c есть метрический тензор связанной узловой сети, или матрица решения, умножение которой на вектор источников I позволяет сразу получить напряжения E c на ветвях сети как преобразование координат.

В двойственной сети матрицы решения меняются местами.

Таким образом, потоки, созданные внутренними источниками, протекают в замкнутых путях. Внутренние потоки не выходят за пределы системы. Потоки, созданные внешними источниками, представлены в базисе разомкнутых путей. Они поступают в систему извне в одних узлах, проходят по ней, и покидают в других узлах.

Внешние потоки и внутренние потоки протекают по одним и тем же ветвям, не взаимодействуя друг с другом. Это происходит потому, что подпространства замкнутых и разомкнутых путей независимы, их матрицы преобразования ортогональны. Двойственность и независимость замкнутых и разомкнутых путей, компонент величин, потоков в этих путях, расширяет возможности сетевого моделирования предметных областей с переменной структурой. Сумма рассеиваемой мощности в данной и двойственной сети остается постоянной при изменении структуры.

Расчет сети при изменении структуры

Рассмотрим расчет сети при изменении структуры соединений, когда меняется число узлов, а, следовательно, меняется число базисных замкнутых и разомкнутых путей. Необходимо получить матрицу решения новой сети по матрице решения старой сети и матрице изменения структуры.

Пусть в старой сети из n ветвей, J1 узлов и одна подсеть, т.е. s1 = 1. Тогда, как показано в (1), (2), базисных разомкнутых путей j1 = J1 – s1, а замкнутых путей m1 = n – j1. Если в новой сети наложены связи, то для этого часть узлов ΔJ соединили с другими, и узлов в сети стало меньше, т.е. J2 = J1 – ΔJ. Тогда уменьшится число базисных разомкнутых путей:

• (8)              j 2 = J 2 – s 1 = J 1 – Δ J – s 1 = j 1 – Δ J ,

а число базисных замкнутых путей возрастет:

• (9)             m 2 = n – j 2 = n – j 1 + Δ J = m 1 + Δ J .

Уменьшение числа узлов увеличивает количество базисных замкнутых путей, контуров, и уменьшает количество базисных разомкнутых путей, и наоборот.

Матрица преобразования путей новой сети через матрицу старой сети, включая матрицу изменений ΔC, имеет вид:

	n		n		n
m 1	mC 1	m i	mV	m 2	mC 1
C a'ia = j 1	jC 1	;                Ca- 2 a =  Am	ACZ	ji            ----------	AC
		j2	jCV	j 2	jC 2
где двойная черта отделяет в матрице C α `2 α подматрицы				C 2 и jC 2 .

В двойственной сети при этом произойдут обратные изменения: разрывание связей, увеличение числа узлов, т.е. становится больше разомкнутых путей, меньше контуров. Если часть узлов разомкнуть, то узлов станет больше J 2 = J 1 + Δ J . Разомкнутых путей базиса станет больше на Δ j = Δ J (число подсетей прежнее), а контуров меньше на Δ m = Δ J . Тогда подматрица Δ C в новой сети переходит от ^mC 2 к ^jC 2 :

n                                    n

m1 mC1 m2 < m1 mCaia Ca'ia = α ;                Ca^2  = Δj ACa'a j2 = j1 jC1 j1 j Ca'2a где двойная линия показывает новую границу между mC2 и jC2.

m 2	mC i
Am	AC
j 1	jC 2

Расчет контурной сети при наложении связей. Матрица решения новой сети имеет такой же вид, как и для старой сети.

• (10)         Y²⁺ c = ^mC 2t (^mC 2 Z ^mC 2t )^{–1 m}C 2

где через Y2+c обозначена матрица решения сети при уменьшении числа узлов. Подставим выражение для матрицы mC2 через матрицу mC1 и матрицу измененных путей ΔC:

n

n

m i    Am

m i

^mC i

n

m i    Am

m i     ^mC i

том 14 № 4 (41), 2018, ст. 1

_Y 2+_{c =}

mC 1t

ΔC t

Δm

ΔC

n

n

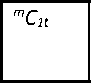
ΔC t

) -1

Δm

ΔC

Преобразуя это выражение, получим матрицу решения новой сети, выраженную через матрицу решения старой сети и матрицу изменения решения – для подпространства замкнутых путей при наложении связей.

(11) Y²⁺ c = Y¹ c + Δ Y c = Y¹ c + (I – Y¹ c Z) Δ C t [ Δ C Z (I – Y¹ c Z) Δ C t ]^–1 Δ C (I – Z Y¹ c ),

где Δ Y c , представляет собой матрицу изменения решения от старой к новой сети.

Матрица решения для замкнутых путей при разрывании связей Y c ^2– в контурной сети получается с помощью инварианта двойственности:

• (12)        Y c ^2– = Y c ¹ – Y c ¹ Δ A t [ Δ A Y c ¹ Δ A t ]^–1 Δ A Y c ¹ = Y c ¹ – Δ Z c

При разделении сети на независимые подсети матрица преобразования и аналитические выкладки имеют более сложный вид, но приводят к таким же формулам расчета сети при изменении структуры [3]. Всего есть восемь формул, которые являются основой алгоритмов расчета изменения структуры; четыре для сети и четыре – для двойственной сети: по две формулы при наложении связей и по две – при разрывании связей. Из каждых двух – одна для замкнутых путей, другая – для разомкнутых путей. Они обеспечивают все варианты расчета сетей при изменении структуры, включая разделение на части и расчет по частям.

Совокупность данных формул, которую можно представить в одной таблице [3, 7], представляет собой обобщенную диакоптику – метод расчета процессов при изменении структуры сетей и сложных систем различных предметных областей, которые можно представить моделями в виде одномерных сетей. Вид формул расчета не зависит от характера изменений структуры – соединение ветвей, разделение сети на части или соединение из частей целого.

Изменения структуры представляет сеть из ветвей, составляющих измененные пути. В нее входят контуры, которые стали разомкнутыми путями, или разомкнутые пути, которые стали контурами в результате изменения структуры. Такие пути образуют матрицу преобразования измененных путей, матрицу ΔC (для двойственной сети ΔA). Эти пути меняют размерность подпространств замкнутых и разомкнутых путей. Метрический тензор такой сети изменений представлен в квадратных скобках формул (11) и (12), а также получаемых из них, с помощью инварианта двойственности, формул расчета других видов изменения структуры. Размер сети изменений зависит от количества разделений и соединений, которые произведены в структуре.

Разделение на части, как и другие изменения соединений, можно делать «разрыванием», выделением части ветвей из сети, но можно просто разделять ветви в узлах, которые их соединяют. Сеть соединений можно рассматривать как «каркас», соединяющий подсети, образуя ту или иную исследуемую конфигурацию. Или рассматривать подсети как набор блоков, составляющие рассматриваемую конструкцию.

Расчет сети при изменении структуры, включая декомпозицию и расчет по частям, происходит без итераций, связанных с учетом взаимного влияния частей в целой системе. После расчета подсистем потоки в сети изменений, «сети пересечений» [1], сразу дают потоки, которые должны быть в целой сети. При этом обращается матрица двойственной к сети изменений структуры, которая содержит измененные пути.

Время расчета сети по частям определяется временем обращения матриц решения подсистем и сети соединений (изменений). Время обращения матрицы пропорционально кубической степени ее порядка, поэтому разделение на части значительно снижает объемы вычислений. Расчет по частям можно проводить с применением параллельных вычислений, например, на суперкомпьютерах.

Для декомпозиции расчета по частям сложных систем необходимо применять методы разделения сети на независимые подсети. Если разделить систему на мелкие подсети, то сеть соединений станет велика, и ее расчет будет сопоставим по сложности с полной системой. Ожидаемая экономия вычислений будет потеряна. Надо разделить целое так, чтобы части и сеть соединений были примерно одного размера. Таким образом, необходимо решать задачу оптимального разделения структуры на части [7].

Диакоптика обеспечивает не только эффективность расчета по частям, и возможность рассматривать системы с переменной структурой, но и позволяет создавать сетевые модели предметных областей различной природы, получая новые знания о скрытых топологических свойствах. Сети с инвариантом двойственности и независимостью замкнутых и разомкнутых путей дают метод моделирования предметных областей.

При изменении структуры сети необходимо заново выводить уравнения поведения и решать их. При частых изменениях, когда расчет каждого вида структуры трудоемок, целесообразно использовать известный результат расчета сети для получения решения сети с другой структурой. Это необходимо, например, для создания банка решений при различных отключениях или переключениях элементов установки, которые могут приводить к авариям.

Применение диакоптики

Сетевые модели объектов нефтепереработки применяются для прогнозирования пожароопасных ситуаций, связанных с изменением (разрушением) частей установок

Сетевые модели обеспечивают расчет изменения процессов при изменении структуры сложных систем различных предметных областей. Расчеты по частям сетевой модели межотраслевого баланса, рассмотренной в [2, 3, 4], обеспечивают ускорение плановых расчетов, анализа структурных реформ, распределения ресурсов для новых производств и технологий. Двойственная сеть представляет потоки денежных средств, что позволяет рассчитать изменения в производстве при изменении финансовых показателей.

Сетевые модели технических и технологических систем, например, объектов нефтепереработки, применяются для расчета вариантов поведения системы при авариях, связанных с разрушением структуры, для прогнозирования пожароопасных процессов [5].

Сетевая модель банка [6] обеспечивает анализ процессов в банковской системе, агрегирование больших данных отчетности в измеримые показатели деятельности, с иерархией рейтинговых оценок банков и индекса состояния всей банковской системы. Этот подход может применяться и в других секторах экономики. Сетевые модели применяются для анализа информационных, технических и телекоммуникационных систем [9-13].

Сетевая модель системы нефтепереработки

В технических и технологических системах сетевые модели обеспечивают расчет поведения при изменении структуры (варианты проектирования, нарушения связей, отключения или подключения подсистем, аварии, и т.д.). Сетевые модели ряда объектов нефтепереработки реализованы на стенде подготовки операторов обеспечения безопасности в Академии пожарной службы МЧС. Результаты представлены на Международном форуме систем безопасности объектов газо- и нефтепереработки в марте 2017 г.

Например, в атмосферной колонне, схема которой представлена на рисунке, на вход подается нагретая нефть. Этот поток под действием перегретого пара проходит снизу вверх в виде парогазовой смеси. На заданных участках циркуляционное орошение понижает температуру смеси. При охлаждении до определенной температуры соответствующая фракция переходит в жидкое состояние и выводится из установки – керосин, бензин, газ. Мазут выводится снизу. В разделении потока нефти на фракции участвуют два основных вида потока энергии – массовые потоки и тепловые потоки.

В сетевой модели атмосферной колонны два вида потоков энергии представлены двумя подсетями. Это контурная сеть с базисом замкнутых путей, внутренние источники, и узловая сеть с базисом разомкнутых путей, внешние источники воздействия. Контурная сеть представляет потоки механической энергии, а узловая сеть – потоки тепловой энергии.

том 14 № 4 (41), 2018, ст. 1

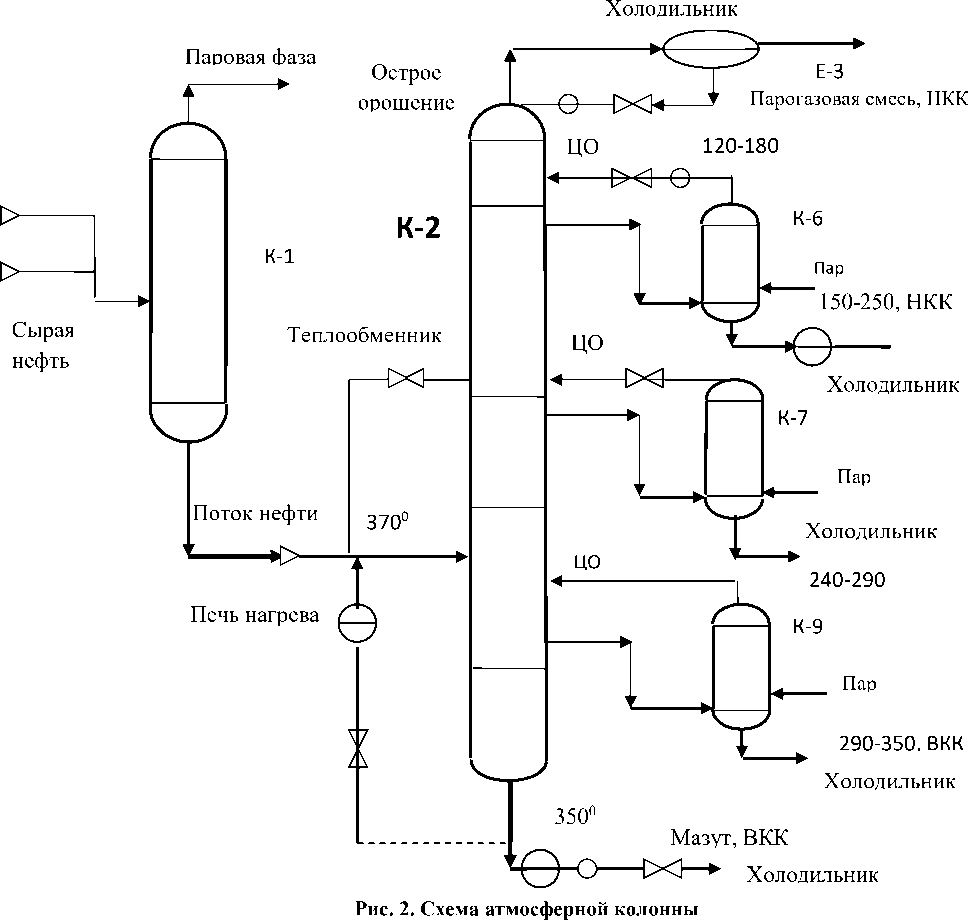
Для установления аналогий между данной системой и сетевой моделью рассмотрены варианты простейшей установки с одним циркуляционным орошением с многими заземлениями и с одним заземлением. Расчеты показали, что наиболее адекватна реальной системе сеть с одним заземлением. Изменения структуры состоят в нарушении путей движение продуктов (например, оседание кокса) или разрыве, отключении различных частей, ведущих к возникновению аварийных ситуаций.

Потоки тепловой энергии представлены в базисе открытых путей с внешними источниками воздействия по аналогии с узловой сетью. Источниками воздействия являются нагреватели и охладители. Тепловые потоки рассчитываются как отклики в узловой сети. Механическую энергию (кинетическую и потенциальную) создают потоки массы нагретой нефти на входе и парогазовой смеси в установке, разделяемой на фракции. Массовые потоки различных фракций рассчитывается как отклики в контурной сети. Источниками воздействия являются насосы, создающие давление.

том 14 № 4 (41), 2018, ст. 1

Сетевая модель атмосферной колонны первичной переработки нефти представлена на рисунке.

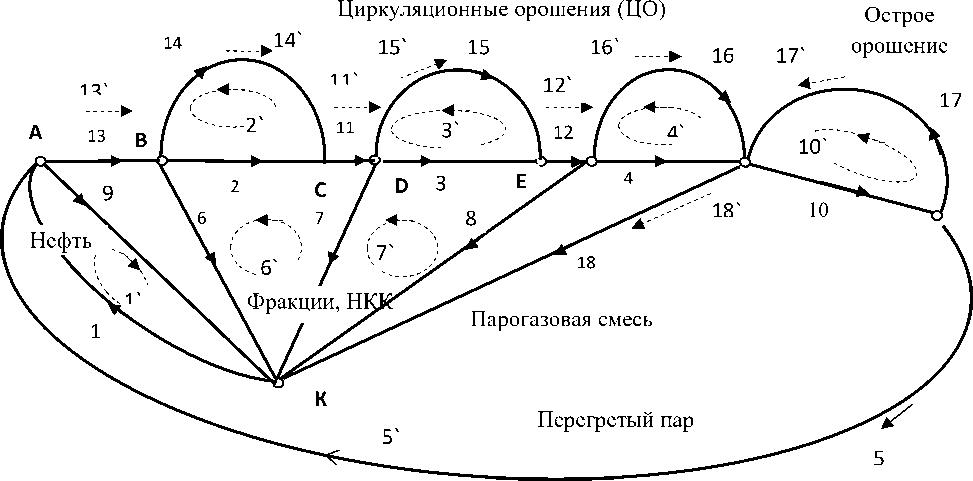
Рис. 3. Сетевая модель атмосферной колонны (три ЦО и острое орошение, цикл перегретого пара), показан выбор путей в структуре

По ветви 1 поступает поток исходного сырья, разделяется на поток мазута в ветви 9 и остальные фракции в ветви 13 вместе с потоком пара из ветви 5. Далее из парогазовой смеси отделяется фракция ВКК по ветви 6. Оставшийся поток проходит три ЦО, выделяются три фракции НКК, включая бензин и газ после острого орошения. В узле К , заземление, сохраняется баланс входного потока и выходных потоков, каждый выводится по своему пути. Подматрица замкнутых путей ^mC сетевой модели установки переработки нефти при переходе от свободных ветвей к связанной сети имеет следующий вид.

1    2   3   4   5   6   7   8   9  10  11   12  13   14  15  16  17  18

1 1 1 m 2 1 -1 m 3 1 -1 m 4 1 -1 m 5 1 1 1 1 1 1 1 1 m 6 -1 1 -1 -1 m 7 -1 1 -1 -1 m 8 -1 -1 1 -1 -1 m 9 1 1 1 -1 m 10 1 1 m www.rypravlenie.ru

том 14 № 4 (41), 2018, ст. 1

Матрица решения контурной сети, позволяющая определить потоки массы в сетевой модели, рассчитана по формуле (6). Ее умножение на вектор источников ЭДС в ветвях (насосы, которое создают давление в установке), имеющих, например, вид.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

150

15

10

14

52

20

25

25

10

10

1

1

1

10

8

12

-6

16

Умножая матрицу решения на этот вектор, получаем отклики в ветвях – частях установки, которые соответствуют потокам массы нефтепродуктов.

Матрица преобразования двойственной сети А применятся для расчета узловой сети. Она преобразует взаимный базис открытых путей, и ортогональна матрице С . Матрица решения для подсети открытых путей Z c рассчитывается по формуле (7). Источники тепловой энергии (нагреватели и охладители) заданы вектором источников тока, отклики на которые представляют аналоги потоков тепла.

Необходимо определить поведение установки при изменениях структуры, например, авариях. В качестве примера на рисунке показана сетевая модель установки, в которой возник разрыв в верхней, шлемовой части колонны. Два контура разомкнулись и стали открытыми путями.

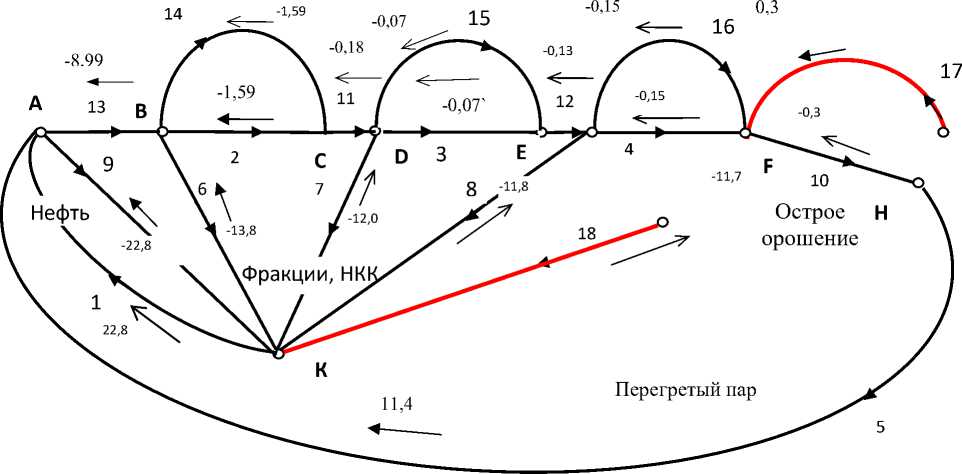
Рис. 4. Сетевая модель колонны с аварией: отрыв ветви 17 от узла Н и ветви 18 от узла F. Контуры 7 и 8 в матрице преобразования стали разомкнутыми путями

Применение алгоритмов преобразования старого расчета сети при изменении структуры. При расчете модели с новой структурой матрица ^m С имеет вид.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 m 2 0 1 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 m www.rypravlenie.ru

том 14 № 4 (41), 2018, ст. 1

3	0	0	1	0	0	0	0	0	0	0	0	0	0	0	-1	0	0	0	m
4	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	-1	0	0	m
5	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	0	m
6	0	-1	0	0	0	1	-1	0	0	0	-1	0	0	0	0	0	0	0	m
7	0	0	-1	0	0	0	1	-1	0	0	0	-1	0	0	0	0	0	0	m
8	0	0	0	-1	-1	0	0	1	-1	-1	0	0	0	0	0	0	0	0	m

Ветви 17 и 18 теперь не входят ни в один контур. Два замкнутых пути, 9 и 10, стали разомкнутыми, соответствующие строки изменились. Эти пути и составляют матрицу изменений. Двойственная матрица изменений путей ΔA описывает разрыв контуров 9 и 10.

1    2    3    4    5    6    7    8    9   10   11   12   13   14   15   16   17   18

-1	0	0	0	0	1	1	1	1
0	0	0	0	-1	0	0	0	0

0	0	0	0	0	0	0	0	0
1	0	0	0	0	0	0	0	0

Расчет сети с переменной структурой по формуле (12) при разрывании связей включает матрицу изменений 2 ⋅ 2, обращение которой проще, чем обращение матрицы 10 ⋅ 10.

9            10

0,575555	-0,11062
-0,11062	0,60376

Обратная матрица (ΔA Yc1 ΔAt)–1 умножается справа и слева на матрицы Yc1 ΔAt и ΔA Yc1, что дает матрицу изменений, т.е. ΔZc. Это уменьшает объемы вычислений, позволяет использовать старые результаты для получения новых решений. Разница между значениями потоков для штатного режима и аварийного режима была рассчитана для значений потоков в единицу времени. Полученная разность будет накапливаться, и можно рассчитать время, за которое избыточные потоки массы создадут аварийную ситуацию. Динамика накопления массы сверх нормативных значений в ветвях установки через выбранные единицы времени (например, секунды) показывает уровень нарастания опасности.

Расчет разных вариантов аварийных ситуаций обеспечивает управление безопасностью. Оператор по комбинациям сигналов датчиков определяет локализацию аварийной ситуации, принимает меры по спасению персонала, включению средств выхода в нормативный режим, или по ликвидации аварии. Методология применяется для создания цифровых сетевых моделей других видов установок и технологий.

Набор основных потенциально возможных аварийных ситуаций для обеспечения безопасности связан с числом базисных путей в структуре установки. Для контурной сети, представляющей массовые потоки, это число независимых контуров, равное 10. Для узловой сети, представляющей потоки тепловой энергии, это число независимых разомкнутых путей, их 6. Надо рассмотреть 16 вариантов нарушений в структуре. Эти варианты составят базовый набор, а остальные можно получить из них как линейные комбинации.

Сетевая модель реализована на стенде подготовки операторов по обеспечению безопасности в Академии пожарной службы МЧС и позволяет управлять процессами предотвращения и ликвидации аварийных ситуаций. Реальные установки содержат сотни и тысячи элементов, поэтому для расчета их сетевых моделей применяются алгоритмы расчета сетей по частям.

Сетевая модель банка

Сетевая модель банка применялась при создании информационно-аналитической системы (ИАС) «Банки и финансы» для банков России, с целью формирования инвариантных показателей работы кредитной организации при изменении систем отчетности, например, при изменении Плана счетов бухгалтерского учета в КО РФ [6].

Результаты применения сетевой модели банков и банковской системы представлены информационными продуктами. В печатной форме это бюллетень «Банки и финансы», издавался при поддержке Ассоциации российских банков в 1995-2012 гг. [6], и ежемесячное приложение «Деятельность банков России». В электронной форме ИАС «Банки и финансы» работает с 1999 г. На основе отчетности накоплены показатели банков России за 20 лет. Ежемесячно по всем банкам осуществляется расчет рейтинга динамической финансовой стабильности (РДФС); а также расчет на основе РДФС индекса состояния банковской системы России (ИСБС). Расчет РДФС осуществляется на основе 7 внешних показателей, определяющих положение банка в банковской системе, и 13 внутренних показателей, определяющих собственную стабильность банка. Расчет осуществляется по месяцам за год с применением формул «постепенного забывания» более старых значений [14]. Показатели выбраны и сформированы по сетевой модели банка.

Мониторинг более 170 показателей деятельности банков является информационной основой для анализа ситуации и управления данной системы. В качестве примеров работы на диаграммах за 15 лет представлены финансовые результаты банков Москвы, расчет ежеквартальный, и динамика ИСБС.

том 14 № 4 (41), 2018, ст. 1

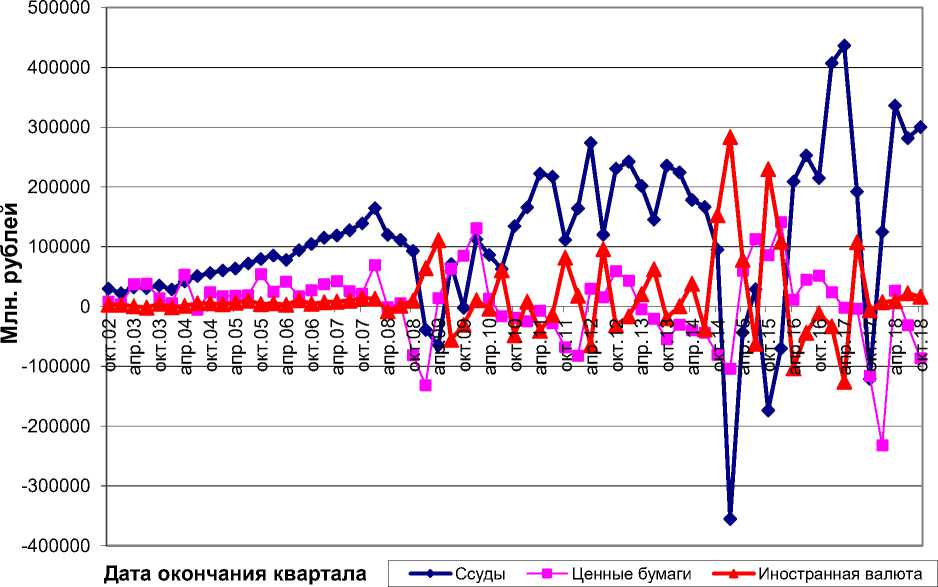
Рис. 5. Динамика финансового результата банков Москвы по отдельным видам операций

До 2008 года наблюдался устойчивый рост по ссудам, спад начался за три квартала до начала мирового кризиса. Введение санкций в 2014 г. привело к значительным убыткам по ссудам, однако затем рост продолжился с колебаниями. Подъемы и спады поступлений по ссудам находятся в противофазе с подъемом и спадом по операциям с иностранной валютой – при подъеме по кредитам падают результаты по валюте, и наоборот. Это волны движения реальных потоков денег в системе. На 1.10.2017 имел место спад по всем видам операций, но к 1.10.2018 фиксируется положительный результат по кредитам в течение годового периода.

Динамика ИСБС дает более сглаженные тенденции развития банковской системы, поскольку на каждую дату учитываются данные по месяцам за 12 отчетных дат.

том 14 № 4 (41), 2018, ст. 1

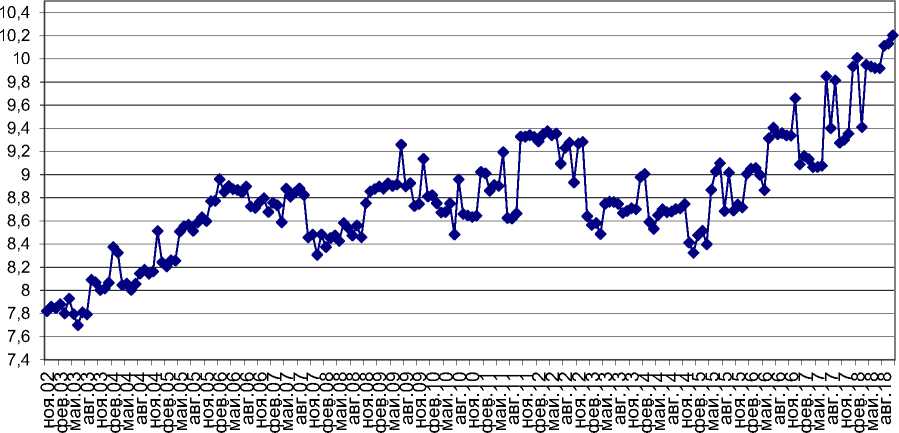
Даты

Рис. 6. Индекс состояния БС РФ, взвешенный (ИСБС-В)

ИСБС показывает стабильный рост банковской системы до 2008 г. Далее после колебаний рост продолжился. В 2012-2013 гг. наблюдалась стабилизация. Спад начался до введения санкций, далее рост продолжился, с колебаниями. Отмеченный выше необычный спад по всем видам операций банков к октябрю 2017 года есть признак очередного кризиса.

Заключение

Сети обеспечивают расчет и анализ сетей с переменной структурой. Это позволяет получить решение для любой структуры как преобразование решения для одной структуры. Например, рассчитать разные варианты конструкции, или поведение системы при различных авариях. Полученные формулы обеспечивают расчет целого по частям без итераций за счет двойственной сети к сети соединения. Топология сетевой модели дает знания, не заложенные в исходной системе. Например, сетевая модель системы производства представляет потоки продуктов комбинацией контурных и узловых токов, благодаря ортогональности их матриц преобразования, а кроме того, дает напряжения, которые пропорциональны добавленной стоимости и потокам денег [3, 4]. Тензорный метод расчета сетевых моделей сложных систем с переменой структурой, по существу является обобщенной диакоптикой, и применяется в задачах конструирования, управления, обеспечения безопасности, проектирования информационных и других систем.