Теорема об одном предельном переходе под знак интеграла

Пусть функции {№)}, измеримы на А . Докажем следующую теорему.

1-теорема. Если выполняются следующие условия:

• 1.    Последовательность функций

  на A сходится к

  
  

• 2.    При всех л

• 3.    Справедливы следующие равенства

где - интегрируема на .

lull [/=(xWr = [ f-(x)dx где

X (x)=max(O,X(x))

X“W = nrni(O.Xm) f~(x} = imx(O, /(xD /"(х) = пшк0./(х)) ,

тогда

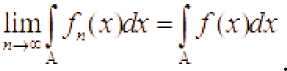
Доказательство. Пусть выполняются условия теоремы. Тогда по теореме Лебега следует, что интегрируема на Aи

11т||Х(х)^ = р/(х^х

.

Из интегрируемости следует интегрируемость /0 на A [5].

Очевидно, что

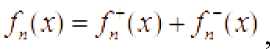
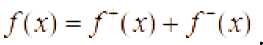
Вычислим пределы

lim j |X (x )^y = lim pXA x) +1 X’( x )| )dr =SK (x)dr + liiii j X~(x)pfr = = jf“(xWr-j|/“(x^r

A            A          .

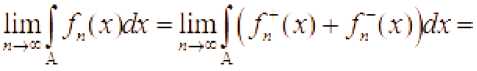
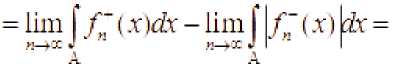
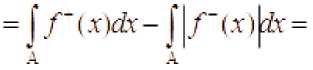
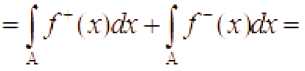
}(/ W-/ Ш^т=У(.гЖ A                   A

Теорема доказана.

Замечание. Поскольку значения, принимаемые функцией на множестве меры 0, не влияют на величину интеграла, в теореме достаточно предположить, что {1^4 сходится к почти всюду и |/>^Vy ^

также выполняется почти всюду.

Литературы.

1. Колмогоров А.Н., Фомин С.В. Элементы теории функции и функционального анализа. М., «Наука», 1989.

"Мировая наука" №5 (98) 2025