Теорема вложения Соболева для анизотропно нерегулярных областей

Известная теорема. вложения Соболева:

Wm(G) С Lq(G), характеризуемая неравенством kfiLq(G)k 6 CkfW(G)k =

= C

(x

\|a| = s

kDaf L (G) k + kf L (G) k s G N,  1 < p < q < ro,

установлена им в 1938 г. (см. [1]) для области G С С R” с условием конуса при s - n + n > 0.               (2)

pq

Соотношение (2) (определяющее максимально возможное значение q в теореме (1)) является и необходимым условием вложения. Результат С.Л. Соболева. был перенесен на. области более общего вида: области классов J n- 1 , Ip 1 _ 1 (В.Г. Мазья, I960. 1975. см. [2]). обла с ти с условном Джона. (John domains; Ю.Г. Решетняк [3,4]), области с условием гибкого конуса. (О.В. Бесов, 1983, см. [5]).

Определение ([6]). При ст >  1 область G С R ⁿ называется областью с условием гибкого ст-конуса. если при некоторых T >  0.0 < к о 6 6 1 для любого x G G существует кусочно гладкий путь

Y = Yx : [0,T] ^ G, Y(0) = x lY'| 6 1 п.в., такой, что dist(y(t), Rn \ G) > к0ta щ)ii 0 < t 6 T. □

В случае ст = 1 такую область называют также областью с условием гибкого конуса. Области, не удовлетворяющие условию гибкого конуса, будем называть нерегулярными.

Для нерегулярной области (которая в окрестности некоторой точки границы может, в частности, иметь вид внешнего пика.) вложение (1) может оказаться неверным пи при каких соотношениях параметров или быть верным при некоторых более сильных, чем (2), условиях, связывающих n, s, p, q и зависящих от геометрических свойств области G. В.Г. Мазья выделил классы областей

I_a (1960), J_p,_a (1975), для которых установил соответственно при p = 1 и при p >  1 теорему вложения (1) для s = 1 с максимально возможным q. Классы I_a, J_p,_a определяются в терминах изопериметрических пли емкостных неравенств.

В [6] показано, в частности, что для области с условием гибкого ст -конуса вложение (1) справедливо при соотношении параметров

, - ^{ст (} n ^- 1) ^{+ 1} + n > 0 . (3) pq

Этот результат при s = 1 принадлежит Килпелай-пепу и Малы [8]. Д.А. Лабутиным установлено [9], что условие (3) является также и необходимым для данного вложения.

В [6-8] содержатся и весовые обобщения неравенства. (1) для области с условием гибкого ст -конуса.

Для областей специального вида, с условием ст -конуса теорема вложения (1) справедлива и при соотношениях параметров, отличных от (3), как показано в работах Д.А. Лабутина. [10] и ВТ. Мазьи - С.В. Поборчего [И].

Б.В. Трушиным [12, 13] выделены специальные подклассы класса, областей с условием гибкого ст -конуса и установлена теорема вложения Соболева. при неулучшаемых соотношениях параметров, различных для разных подклассов.

В данной работе мы расширяем сравнительно с [12] классы областей, для которых справедлива, теорема, вложения Соболева, в формулировке [12], обобщая тем самым соответствующие результаты Б.В. Трушина. Метод работ [6, 7, 12, 13] опирается, в частности, на оценки слабого типа (1 , 1) для максимального оператора. Харди-Литтлвуда, и его анизотропного аналога. Здесь мы привлекаем обобщение анизотропного максимального оператора. Харди-Литтлвуда, построенное по дифференциальному базису, содержащему прямоугольные параллелепипеды, ребра, одних из которых не обязательно параллельны ребрам других.

Схема данной работы такова. Для области G определенного типа, строится семейство гибких конусов (содержащихся в G ), «выпущенных» из каждой точки x Е G. Строится интегральное представление функции f через ее производные D^af, |о| = s, по гибкому конусу, из которого следуют поточечные оценки функции через интегралы, содержащие соответствующие производные. Этим получение оценки вида. (1) сводится к получению оценок соответствующих интегральных операторов. Два. основных интегральных оператора, сначала. оцениваются через максимальный оператор, строящийся по дифференциальному базису, соответствующему заданному семейству гибких конусов. Слабая (1 , ^-ограниченность максимального оператора влечет слабую ( p, q ^ограниченность упомянутых операторов. Последняя в силу интерполяционной теоремы Марцинкевича, влечет ( p, q ^ограниченность этих операторов, а значит, и оценку теоремы вложения.

В силу сказанного реализация указанной схемы для данной области G должна начинаться с построения согласованных между собой семейства, гибких конусов и дифференциального базиса. Такое построение определяется геометрическими свойствами области G.

I. О покрытиях типа Безиковича

Везде далее N — множество натуральных чисел; n Е N, n > 2; R ⁿ — n -мериое евклидово пространство; область G С R ⁿ, G = R ⁿ, х — характеристическая функция интервала (0 , 1). Для измеримого по Лебегу множества E С R ⁿ через |E| обозначается его лебегова, мера.

При 16p<∞ kf kp,E = kfL (E) k,

n

A = ( A i , ..., An ) Е [1 , ro ) n, min Xi =1 , |A|       Xi,

16 i 6 n              ■'—^

i =1

x = ( x ₁ , . .., xn ) Е R n, |x| a = max |xi| ^{1 /A} i , 16 i 6 n

^|x + У^|A 6 ^|x|A + ^|y^|A.

Мы перенесем некоторые свойства, покрытий множеств в R ⁿ типа покрытий Безиковича (см. [14, 15]), известные для случаев покрытий шарами или параллелепипедами с ребрами, параллельными координатным осям, на. случай покрытий повернутыми прямоугольными параллелепипедами.

Далее будем считать, что в R ⁿ задано некоторое семейство операторов поворота $ ⁰( x ), зависящих от параметра x Е R ⁿ (т.е. линейных изометрических операторов с det $ ⁰ ( x ) = 1). Ч срез $ ( x ) будем обозначать оператор

$ (x) y = x + $ 0( x)(y — x) V у Е Rn, который будем называть оператором поворота, относительно точки x, соответствующим оператору $0(x). Oneратор $0(x) ($(x)) может также за висеть от дополнительного параметра d > 0; в таком случае будем обозначать его через $0(x,d) ($(x, d)).'

Через P ( x ) будем обозначать прямоугольный параллелепипед с центром в точке x и с ребрами, не обязательно параллельными координатным осям. При 9 >  0 через 9P ( x ) будем обозначать прямоугольный параллелепипед, подобный данному, с центром подобия в точке x и коэффициентом подобия 9.

Положим при d >  0

n

Q _a ( x,d ) := x + Y[ —d^A i ,d^A i ] .

i =1

Множество вида.

$ ( x,d ) Q a ( x,d )               (1.1)

будем называть A -параллелепипедом с центром в точке x.

Определение 1.1. Пусть E — ограниченное множество в R n. и пусть ч,ля каждого x Е E задан прямоугольный параллелепипед P ( x ), причем sup { diam P ( x ): x Е E} < ro. Пзсть 0 < 9 <  1 < < к < ro.

Будем говорить, что покрытие {P(x)}Ж£Е обладает свойством 9-отделимости, если из x,y Е E, P(x) П P(у) = 0, уЕ P(x), |P(у)| 6 2|P(x)| следует, что (9P (x)) П (9P(у)) = 0.

Будем говорить, что покрытие {P(x)}ж£е обладает свойством к-поглощения, если из x,y Е E, P(x) П P(у) = 0, уЕ P(x), |P(у)| 6 2|P(x)| следует, что P(у) С кP (x).                      □

Теорема 1.1. Пусть к >  1 и пусть {Р ( x ) }_Ж£_Е — покрытие ограниченного множества E со свойством к -поглощения.

Тогда, из него можно выбрать конечную или счетную последовательность прямоугольных параллелепипедов {Pk} = {Р ( x(^k )) } , удовлетворяющую при 9 = 1+12 _к условиям

• (i)    E С S Pk ;

• (ii)    ( 9Pk ) П ( 9Pm ) = 0 Vk,m, k = m.        □

Лемма 1.1. Пусть {P ( x ) }_Ж£_Е — покрытие ограниченного множества E С R ⁿ со свойством 9 -отделимости, 9 Е (0 , 1). Тогда из него можно выбрать конечную или счетную последовательность прямоугольных параллелепипедов {Pk} = = {P ( x ^{( k} ) } . удовлетворяющую условиям i, ii. □

Доказательство леммы проводится по стандартному плану доказательства, для случая покрытий кубами (см. [15]). Положим а ₀ = = sup {|P ( x ) | : x Е E}. Выберем прямоугольный параллелепипед P ₁ = P ( x ⁽¹⁾) Е {P ( x ) }_Ж^_Е таким, что |P ( x ) | > a0. Пз"сть P ₁ Pm уже выбраны.

m

Если E \ [J Р_к = 0, то процесс выбора закончен. к =1

В противном случае положим

am

sup{ |Р ( x ) |

: x Е E

m

\ и Pk} к = 1

и выберем прямоугольный параллелепипед

Pm +i = Р(x(m+1)) Е Р(x): x Е E \ [ Pk к=1

Пусть А Е [1, го)n. 0 < dо < го. G — открытое множество в Rn. Для каждого x Е G через! Bx(x) обозначим семейство А-параллелепипедов $(x,d)Qx(x,d) вида. (1.1) при 0 < d < d0 < го. Объединение этих семейств Bx = U Bx (x) бу-x∈G дем называть дифференциальным базисом па. множестве G (см. [14]). При к > 1 будем говорить, что дифференциальный базис Bx обладает свойством к-поглощения, если из

таким. ЧТО |Pm +1 | > am.

Покажем, что выполняется условие (i): E С С |j P_k. Если процесс выбора обрывается на конечном шаге, то условие (i), очевидно, выполнено. Пусть {Р_к} — бесконечная последовательность. Тогда. |Pk | ^ 0 щ hi k ^ го. так как {Р ( x ) }xeE — ^ -отделимое покрыт нс. в силу чего ^2 |6Р_к| < ∞

< го. Если найдется x Е E \ |J Р_к. то сушест-1

вуст такое число m + 1. Ч’то |P_m +1 | <  2 |P ( x ) | . что противоречит выбору точки x ^{( m +1)}. Этим установлено свойство (i). Свойство (ii) следует из 0 -отделимост11 покрытия {Р ( x ) }xeE ii способа, построения последовательности {Р_к}.

Доказательство теоремы 1.1. Достаточно показать, что свойство к -поглощения покрытия {Р ( x ) }_xGE влечет свойство 0 -отделимости этого покрытия при 6 = 1+12 _К , ^и воспользоваться леммой 1.1. Пусть x, у Е E. и пусть Р ( x ). Р ( у ) — два. таких прямоугольных параллелепипеда, что

P ( x ) П Р ( у ) = 0 , у /Р ( x ) , |P ( У ) | 6 ² Р ( x ) |, кР ( x ) D Р ( у ) .

Покажем, что ( 6Р ( x )) П ( 6Р ( у )) = 0 щ hi 6 = = 1+12 _к ' Достаточно Р^ассмотреть случай x = 0

n и Р(x) = П [—ai,ai]• Без ограничения общности i=1

будем считать, что у 1 > а 1. Пусть

6 Е (0 , 1) , ( 6Р ( x )) П ( 6Р ( у )) = 0 , z Е ( 6Р ( x )) П ( 6Р ( у )) .

Поскольку Р ( у ) С кР ( x ). имсем |z 1 — у 1 | 6 2 к6а 1. Из z Е 6Р ( x ) имсмм |z 1 — у 1 | >  (1 — 6 ) а 1. Из последних двух соотношений следует, что 2 кба 1 > >  (1 — 6 ) а 1. откуда 6 >  1+12 _к ■ Поэтому ( 6Р ( x )) П П ( 6Р ( у )) = 0 пр и 6 = 1+12 _к • Этим теорема доказана.

Примером покрытия (ограниченного) множества E С R n со свойством к -поглощения является покрытие E шарами или параллелепипедами вида (1.1) при $ ( x,d ( x )) = Id, d ( x ) Е Е (0 ,d ₀). Более общим примером покрытия со свойством к -поглощения является покрытие сравнимыми прямоугольными параллелепипедами (см. [14, § 1, замечание (5)]). Далее будем иметь дело лишь с покрытиями множества. А -параллелепипедами (1.1) при фиксированном А = ( А 1 ,..., An ) Е [1 , го ) n . min Ai = 1.

x, у Е G, $(x, d 1)Qx(x, d 1) П $(у, d2)Qx(у, d2) = 0, у / $(x, d 1)Qx(x, d 1),   |Qx(у, d2)| 6 2Qx(x, d 1)| следует, что к$(x,d 1)Qx(y,d 1) D $(y,d2)Qx(y,d2). Введем максимальный оператор, построенный по Bx на. миожестве G для f Е L(G, 1с>с):

M x, (x ):= sup

0 0

|$ ( x,d ) Qx ( x,d ) П G|

×

x У        Vf ⁽ у ) | ^dУ.

< ( x,d ) Q _x ( x,d ) nG

Теорема 1.2. Пусть дифференциальный базис B_x на миожестве G обладает свойством к -поглощения при некотором к >  1. Тогда, для каждого т >  0 выполняется неравенство

|{x Е G: M x,< f (x) >т} 6 C kf |L 1( G) k, (1.2) τ где C не зависит ни от f. 1111 от т.               □

Доказательство теоремы аналогично дока зательству соответствующего утверждения теоремы 1 из [16. §1].

Приведем в случае n = 2 пример области G Е Е R² и связанного с ней дифференциального базиса. вида. {$ ( x,d ) Qx ( x,d ) } x _G g, 0 0 co свойством к -поглощения. Пусть А = (2 , 1). Qx ( x,d ) = = x + [ —d ² , d ²] x [ —d,d ]. Опишем сначала область G С R ⁿ и построим на ней семейство (усеченных) гибких конусов (которые впоследствии будут служить носителями интегрального представления функций через производные). Построим затем требуемый дифференциальный базис, согласованный с этими гибкими конусами. Начнем с некоторых вспомогательных построений.

Пусть к Е (0 , 1), R Е (2 , 1). Построим кривую

д( k,R ) = 7 1( k,R ) U Y ²( k,R ) , где Y 1( k, R ) является частью окружности радиуса R с центром в точке

₍         ) - ( 1 — R к (1 — R ) ^

(xk,R,ук’^   у vm2, vr+k2) ’ лежащей в угле {(x,y): x > xk,R, Уk,R. < у < kx}. а Y2 — вертикальным лучом, исходящим из нижней ZS точки дуги y 1 (k, R) и направленным вниз. Точнее говоря,

71(k,R) = {(x,y): (x — x^r)2 + (у — ук^.)2 = R2, yk,R 6 y < kx ,

7^{2( k,R} ) = {^{( x,}У ^{): x} = xk,R ⁺ R, у 6 ук^.

y

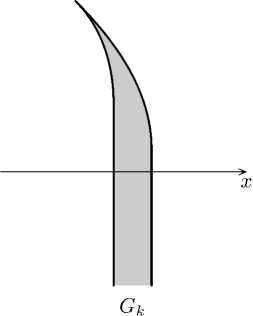
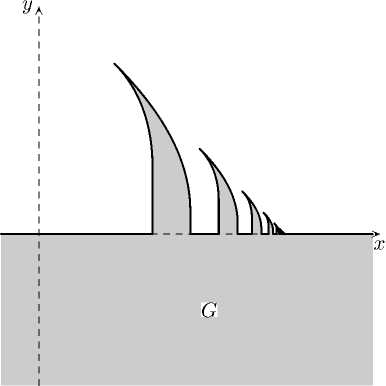
Рис. 1

Отмстим, что луч Y 2( k,R ) касается 71 ( k,R ) в точке ( Xk,R + R,yk,R ). Положим Gk = U ^{Y ( k,R} ) ^С (^{( Х,}У ^): К ¹ 1 2

2 1                     ^{1 + k} 2

Дуги

< 4

(см. рис. 1), так что Gk лежит в вертикальной полосе ширины меньше 2 к .

Пусть R - : = { ( х,у ): у <  0 }, e ¹ = (1 , 0). Рассмотрим область

G :

∞

U (Gkj j=1

- 2 -j e 1)

U R -

где 2 ^{j 1} 6 kj <  2 ^j.

Отметим на области G семейство кривых

Yj (R) := Y( kj ,R) - 2-j e1, где j e N, 2 < R< 1, с помощью которых построим на G дифференциальный базис. Он состоит из всех прямоугольников вида.

$ (( х,у ) ,d ) Qx (( x,y ) , d ) =

= $ (( х,У ) ,d )(( x,y ) + [ -d ² ,d 2] x [ -d, d ]) ,

(x,y) e G, 0 < d < d0 < 1, расположенных следующим образом. Большая сторона, прямоугольника, либо вертикальна, либо отклоняется от вертикали на. угол, не превосходящий 4. Если точка (х, у) лежит на кривой 7j (R) и у > 0, то середина нижней из малых сторон прямоугольника, также лежит на. этой кривой в точке ее с ординатой, меньшей чем у. Таким образом, большая полуось прямоугольника. $((х,у), d)Q\((х,у),d), расположенная ниже его центра, является хордой кривой Yj (R)• Если же у < 0, то $((х,у), d) = Id. Геометрически довольно ясно (можно убедиться и аналитически), что построенный дифференциальный базис обла дает свойством к-поглощения при некотором к > > 1.

Построим семейство (усеченных) гибких конусов представления функций.

Пусть ( х 0 ,у 0) e G. Построим ось конуса с вершиной в точке ( х о ,у о). Пусть сначала ( х о ,у о) e e R - . Тогда в качестве оси конуса возьмем кривую

Y (хо ,у о) := {(хо ,у): у = у о - t, 0 6 t 6 T}, а. в качестве усеченного гибкого конуса, представления функций U Qx((хо,уо - t), 2\

0

Пусть теперь ( х о ,у _о) e G \ R - ². Тогда, в качестве оси гибкого усеченного конуса, возьмем кривую

Y ^{( х} о ,у о) = Y о^{( х} о ,у о) ^{U Y}j ^{( x}j,у о)

с началом в точке ( х _о ,у _о), г де y о( х о ,у о) — горизонтальный отрезок, соединяющий точку ( х о ,у о) и точку ( Xj,у о) кривой 7 j (4). а кривая 7 j ( Xj,у _о) является дугой конечной длины кривой Yj ( 4 ) имеет начало в точке ( Xj,у _о) и расположена от этой точки вниз. Кривую y ( х о ,у о) параметризуем с помощью параметра t , квадрат которого на y о( х о , у о) совпадает с длиной отрезка y о( х о ,у о) отсчитываемой от точки ( х о ,у _о) (0 6 t 6 t ( х о ,у _о)), а на Yj ( Xj ,у о) t = t ( х о ,у о) + и. где и — длина, дуги Yj ( Xj,у о). отсчитываемая от точки ( Xj,у _о) в сторону уменьшения ординаты у кривой Yj ( Xj,у _о), причем 0 6 и 6 T - t ( х _о , у _о) (такая специальная параметризация нужна, чтобы выполнялись условия определений следующего раздела).

Точку кривой y(хо,уо) со значением параметра. t будем для краткости обозначать y(t)■ 0 6 6 t 6 T. Обозначим через Q(X) прямоугольник Qx, повернутый на угол, «достаточно близкий» к углу отклонения касательной к кривой y (на ее ие-горизоитальиом участке) от вертикали, не коикре- тизируя сейчас оператор поворота $t: Qx (Y(t)) ^ ^ QX)(y(t)) (на горизонтальном участке угол поворота. равен пулю). Построим гибкий усеченный конус представления функций в виде

[ Q х )( Y ( t ) ,r ( x о ,У 0) + et ) ,

0  0, e > 0 столь малы, что

[ Qx ) ( Y ( t ) , 2( r ( x 0 ,y o) + et )) c G.

0 6 T

• II.    Класс рассматриваемых областей и основная теорема

Определение 2.1. Пусть G ₀, G — открытые множества, в R n. G ₀ С G. X = ( A ₁ Xn ) Е Е [1 , ж .) n. min Xi = 1. d ₀ Е (0 , ж .). к >  1.

i6i6 n

Пусть на G ₀ задан дифференциальный базис со свойством к -поглощения и со свойством монотонности:

$ ( x,h ) Q_x ( x,h ) С$ ( x, d ) Q_x ( x,d ) щ hi h < d.

Пусть для каждого x Е G ₀ заданы кусочно гладкий путь y = Yx : [0 , tx ] ^ G- Y (0) = = x. непрерывная кусочно гладкая функция r = = r_Y : [0 , tx ] - (0 , ж ), семейство операторов поворота $t = $t ( Y ( t )) и семейство сопровождающих Y X -параллелепипедов {$tQx ( Y ( t ) ErY ( t )) } 06 t 6 tx co следующими свойствами.

• 1    ° . Усеченный гибкий конус

S (2 $tQx ( Y ( t ) ErY ( t ))) ^{лсжIIT B} G 06 t 6 t x

2°. 3 e ₀ Е (0 , 1): r ( tx ) >  e ₀ Vx Е G ₀.

3 °. Yx ( t ) E$ ( x,t ) Qx ( x,t ) Vt Е [0 ,tx ].

4 °. Матрица, преобразования $_t = $_t ( y ( t )) непрерывна. и кусочно непрерывно дифференцируема. по t. Производные по t от r. y и коэффициентов матрицы преобразования $_t ограничены числом, не зависящим от x, t , при чем |y '| 6 1

5 °. 3e i >  0: $tQt ( Y ( t ) r ( t )) С $ ( x,d ) Qx ( x,d ) ^ ^ r_Y (0) + 1 > e 1 d.

6°. 3 C_o >  0: R Цтг x ( ^№t 1 y ^— Y ⁽ t ) ^,A ) dt 6 Co

⁰                r _Y ( t ) ^A V r _Y ( t )                     ⁰

Vx Е G 0. Vy Е G.

Тогда будем писать G ₀ Е G ( G,X ).           □

Определение 2.2. Пусть G = S G_b Gk Е i

Е G ( G, X^k ). Л := max |X^k |. Тогда oimcm писать i6 k 6 k 0

G Е G (Л).                                     □

Определение 2.3. Пусть X Е [1 , ж ) n, min Xi = = 1. ст >  1. Булем говорить. что множество G 0 удовлетворяет условию X -анизотропного гибкого ст -конуса относительно множества. G. и писать G 0 Е G ( G,X,ct ). ее ли G ₀ Е G ( G, X ). и при этом для каждого x Е G 0 для функции r_Y из определения класса. G ( G, X ) справедл! 1ва оценка. r_Y ( t ) >  c ₀ t^a при t Е (0 , tx ]. цде c 0 >  0 не за.В1 iciit от x Е G ₀.        □

Определение 2.4. Пусть G = S G^ Gk Е k =1

Е G ( G,X^k, ст ) nj>ii k = 1..... k 0- Л = max |X^k |. Тогда будем говорить, что множество G удовлетворяет условию гибкого (Л , ст )-коиуса, и писать G Е ЕG (Л ,ст ).                         ’                 □

При 5 >  0 вве.дем G5 := {x Е G : dist( x,dG ) > > 5}.

Теорема 2.1. Пусть ст > 1, G е G(Л,ст), 1 < < p < q < ∞, s - ст(Л - 1) + > +Л > 0. pq

Тогда для f Е Ws (G) справедлива оценка kfiLq (G) k 6 c( X kDaf iLp (G) k + kfiLp (GS) k), a=s

5 = e Л ,   (2 . 1)

где постоянная C не зависит от f.

ст (Л — 1) + 1

Ьсли при этом s — —--p-2--- + q > 0, то утверждение справедливо при 1 6 p < q < ж.  □

Доказательство теоремы базируется на. всех последующих рассмотрениях и будет приведено в конце работы.

• III.    Интегральное представление функций и поточечные оценки

При выводе интегрального представления функции будем предполагать, что опа. бесконечно дифференцируема, па. открытом множестве — области своего определения.

Пусть x Е G 0. Г = (Г1.....Г n ): [0 ,tx ] ^ G. r = ( r ₁ rn ): [0 ,t_x ] ^ (0 , ж ) ⁿ — непрерывные кусочно гладкие функции, | Г '| 6 1, ri (0) = 0, 0 < < ri ( t ) 6 t при t >  0 it = 1..... n). оператор $_t = $_t (Г( t )) поворота отпосптслыю точки Г( t ) — непрерывное кусочно гладкое по параметру t преобразование. Положим $ °*( y ) := $_t (Г( t ) + у ) — — Г( t ). Пз"сть {ei}” — стандартнын базис в R ”.

^ 0 ei = P aij ( t ) ej.

j =1

$ 0 y = $ 0

i =1

yiei

n

= Eyi$0 ei = i=1

nn

= E E yiaij ( t ) ej = i =1 j =1

nn XX j=1  i=1

aij ( t ) yi   ej .

Пусть

^ Е C 0°° (R¹) ,

j ш ( t ) dt = 1 ,

supp ш Е [0 , 1] ,

n

ⁿ⁽ y ) = Y ^{ш (} yi ) .

i =1

Положим ft(x) = /II 4a ш f yiTTA ) f (Г(t) + $0y) dy = i=1 ri (t)      ri(t)                   t

= У fi( y ) f (Г( t ) + $ 0( r ( t ) y )) dy, (3 . 1) где r ( y ) := ( r i( t ) rn ( t )). Замет им. что ft ( x ) ^ ^ f ( x ) щ hi t ^ 0.

h^{ft (} x )

I

n

П(y)£ Dj f (Г(t)+ $0(r(t)y)) x j=1

x

{ Г j (t) + X i=1

[ aij ⁽ t ) ri ⁽ t ) yi ⁺

aij ⁽ t ) ri ⁽ t ) yi ]}

dy =

Заметим, что при s = 1 оценка (3.5) совпадает с (3.3). Допустим, что при некотором s > > 2 оценка. (3.5) верна. при замене в ней s на. s — — 1. Докажем, что тогда она верна в виде (3.5). Зафиксируем t и y, а значит, и $ ⁰ в ее подынтегральном выражении ( y E Q ⁽ t )(Г( t ) , r ( t ))). При y = = Г( t ) построим путь Г _t : [0 ,t_x — t + r ( t )] ^ G ii вектор-функцию p = ( p^x 1, ... , p^{X n} ), г де p : [0 , tx — — t + r ( t )] ^ [0 , ro ).

Положим u* = Iy — Г( t ) Ix- u* : = tx — t + r ( t ).

= /П   <^5 )Ё Djf (Г( t)+ i=1 ri(t)      ri (t) j=1

^Г t ⁽ u ) =

+ $ 0 y )

n

Гj (t ) + E aij i=1

r_i⁰ ( t )

⁽ t ) yi ⁺ aij ⁽ t ) ri ( t )

yi

dy.

Отсюда.

y + $0[( UU;)x x x ($0)-1(y — Г(t))], Г( t),

Г( t + u — r ( t )) ,

^{0 6} u ⁶ u*. (3,_G) u* 6 u 6 r ( t ).' r ( t ) 6 u 6 u*.

df (x) 6 C /П    Д-yl) x gt j ” I JI1 ri (t)   ^ri (t )J

о _{( u} ) = Z u               ^{npn 0} <^u< ^{r (} t )'

^P [ r ( t + u — r ( t )) при r ( t ) 6 u 6 u* ■

n x^ IDj f (Г(t)+ $0y) | dy. (3.2)

j =1

Оценка. (3.3) для y E QXt )(Г( t ) , r ( t )). пути Г _t. (функции D^e f вместо f пр и I^I = s — 1 и вектор-функции

p дает

В силу теоремы Ньютона-Лейбница:

ID^ef ( y ) I 6

t x n

If ( x ) I 6 C / Y ri ( t ) " ¹ 0 i =¹

n

J £ | Dj f (Г( t ) +

0 6 yi 6 ri ( t ) , j = ¹

u ∗

6 Cju-Wj X D^f (Г t ( u )

0      |_Z| _A <_M^|a| = ^s

+ $ ⁰ z ) I dz du +

i = 1 ,...,n

r ⁽ t )

Лемма 3.1. Пусть область G C R ⁿ, R >  0, A E [0 , ro ) ⁿ . min Ai = 1. x E G. Г: [0 ,t_x ] ^ G — кусочно гладкий путь, Г(0) = x, r : [0 ,t_x ] ^ [0 , ro ) — непрерывная кусочно гладкая функция, r (0) = 0, r ( t ) >  0 щm t >  0. Плтть $_tQ_X (Г( t ) , r ( t )) C G. |r⁰ ( t ) | 6 C ₁. | Г 0 ( t ) | 6 1 для п.в. t E [0 ,t_x ]. коэффициенты aij матрицы пре'образования $ ⁰ — непрерывные кусочно гладкие функции от t , причем H jI 6 C 2.

Тогда.

+ C

j u^-^ X ID^af (Г( t )

u *       | z | a <^| U ^| = ^s

+ $_t ⁰ z ) | dz du +

u∗

+ C^r ( t—r ( t )+ u ) ^-|X|j' X । । = | D^af (Г( t—r ( t )+ u )+

r ( t )

| z | a 6 r ( t-r ( t )+ u )

⁺ $ ⁰ -r ( t )+ uz ^{1 dz du + I (} D^{e f} ) t x ^{( x} ) ^I. ⁽³ . ⁸⁾ Первый из интегралов no z b (3.8):

1 1 =       У X ID^af ( z ) I dz.

I ( $ 0) - 1( z- г t ( u )) |_A<u, ^|a| = s | ( $ 0) ^- 1( z- г( t )) |_A (t)

t _x

If ( x ) | 6 C j ts- ¹ r ( t ) -1^1 У X Df (Г( t )+ о                   |y|<^ ( t ) ^a| = s

+ $ 0 y ) I dydt + C

j If (Г( tx )

⁺ $ ⁰ x y ) ^I dy,

(3 . 4)

^|У^| Л <Г ⁽ t x )

где C = C ( C ₁ , C ₂) не зав1 iciit от fax E G.      □

Доказательство. Установим сначала, что в

условиях леммы

t _x

If ( x ) I 6 C y ts- ¹ r ( t ) ^-|A| У X ID^af (Г( t )+ 0                      |y|(t) ^|a| = s

Ho

($0)-1( z—Г t (u)) = ($0)-1( z—y — (-) X (y—Г( t))), u∗ так что неравенство I ($0)-1(z—Гt (u)) Ix < u влечет неравенство

λ

( $ 0) ^{- 1} ( y — Г( t )) + u 6 u_∗                       λ

6 - I ($0)-1 y — Г(t) Ix + u 6 2u, u∗ откуда

1 1 6        У X ID^af ( z ) I dz.

I ( $ 0) ^- 1( z-y ) |_л 6 2 u, ^|a| = s

| ( $ 0) ^- 1( z- Г( t )) |_A (t)

+ $ 0 yI ) dydt + C ]Г I ( De f ) t x ( x ) I, (3 . 5) |в| 6 s- 1

где C не зависит от fax E G.

Второй из интегралов no z b (3.8)

¹ 2 =    / X |a| = ,ID^a/ ( z ⁾ I dz’

| ( ^ 0 ) ^- 1 ( z- Г( t )) | л

u E [ u*,r ( t )] .

Но ( № 0) - 1( г - Г( t )) = ( № 0) - ¹ ( г - у ) + ( № 0) - 1( у — — Г( t )). откупа при | ( № ⁰) 1( г — Г( t )) |д < и имеем

| ( № 0) ^- 1( г — у ) |_л 6

6 и + | ( № ⁰) ^- 1( у — Г( t )) |д = и + и* 6 2 и.

Так что

1 2 6        У X lD^af ( г ) | dг.

I ( $ 0) - 1( z-y ) |_A 6 2 u,     l^al ^_ s

I ( $ 0) ^- P z- Г( t )) A (t)

Следовательно, из (3.8) имеем

|D^вf ( № 0 у ) | 6

r ⁽ t )

6 C p ' j X _|a| _ _sD^af ( № 0 г ) | dz du +

0     ^{| z —} y ¹ a 6² u,

^{| z - Г(} t ) A⁽t)

t _x

+ C J r ( и ) -^|Л| I X D^af (Г( и ) + № иг ) | dz du + t           |_Z| A ( u ) ^|a| = s

+ | ( De f ) t x ( x ) |.

Отсюда. при |у — Г( t ) |д < r ( t )

Df ( № 0 у ) | 6 Cil|г — y|¹-^|x| X |D^af ( № 0 г ) | dz +

Iz-ylA 6 2 r ( t ) ,                ^{|a| _} s

^{| z - Г(} t ) |A<^{r (} t )

t _x

+ Cjr ( и ) "^ X _aHs |D^af (Г( и ) + №Uz ) | dгdu + t        | z | A ( u )

+ | ( D^e f ) t x ( x ) |. (3 . 9)

t _x          t _x

+C4r(t)|д| У ts-2 У r(и)-|Л|х х У X |Daf (Г(и) + №Uz)| dгdudt+ |z|A

+C X |(D^ef)tx (x)|. (3.10)

|в| 6 s-1

Меняя порядок интегрирования во втором слагаемом и вычисляя интеграл по t, с учетом ограниченности r(t) получаем оценку (3.5).

Оценим слагаемые |D^в|, |^| 6 s — 1, из правой части (3.5). Используя определение ft и применяя при 0 < |^| 6 s — 1 интегрирование по частям, получаем

| (D^e f) tx (x) | 6 ce У lf (Г( tx) + №0 у) | dy. (3.11) ^|У^|А<^{г (}tx )

Из (3.10), (3.11) следует (3.4).

Лемма 3.2. Пусть G₀, G — открытые множества. в Rn. G0 Е G- X = (А 1 An) Е [1, ж). min Xi = 1.

Пусть для каждого x Е G₀ заданы кусочно гладкий путь 7 = Yx: [0, tx] ^ G. y(0) = x- непрерывная кусочно гладкая функция r = r_Y : [0, tx] ^ ^ (0, ж) II семейство сопровождатотпих y Х-параллелсшипедов {№tQw(y(t), r(t))}0616tx co свойствами 1, 2, 4 из определения 2.1.

Тогда для f Е C^ (G), x Е G₀ справедлива оценка.

Проинтегрируем это неравенство по у Е {у: |у — — Г(t)|д < r(t)} С {у: |у — г|x 6 2r(t)}. Заметим предварительно, что

I |г — y|\ ^|X|dy 6 У |w|Д^Д|dw 6 C2r(t). |y - Г( t) |а<г (t)               Мл 62 r (t)

|f (x) | 6 CA J X |D^af |) (x)+ \ |a| _ s         /

+CA2! X |D^af |) (x) + CAзf (x), \|а| _ s

(3.12)

Тогда.

I D^ f (№0 у) | dy 6

^|y^-Г(t ) ^|A<^r(t )

6 C3r(t)   [ X, . |D^af (№0г)| dг+

J         ^|a|_s

^|z-Г(t ) ^|A<^r(t )

+Cr(t)|д| j’r(и)-|AyX|a|_s |Daf (Г(и)+ t         |z|A

+№ Uz ) | dгdu + r (t) ^|A|| (D^e f) tx (x) |.

где

rY (0)

A 1 g(x)= У ts^{-1 -|д|} У g(x+№0у) dydt,

|y|λ_x

A2g(x) = У (t + rY (0))

^s-1rY (t)^-|д|х

×

I    |g(Y(t) + №⁰у) | dydt,

Подставляя эту оценку в неравенство (3.5), в котором s заменено на s — 1, получим оценку

|У|А<Г₇ (tx )

A3^{f (x})=    У    ^{|f (}Y⁽t^{) + №0}_xу)^{| d}У^,

|y|₇ (tx )

• (3.13)

• (3.14)

(3.15)

lf (x) | 6

6 C4Уts-²r(t)1^-wj^X_|a|_ \D“f (Г(t)+№0г)| dгdt+

а постоянная C не зависит от f, x, y, r_Y.       □

Доказательство. По данному пути y и функции r = r_Y постро!IM путь Г:

^|z|A<^r(t )

^Г(t )={Y (°—

при 0 6 t 6 r(0).

r(0)) пpn r(0) 6 t 6 tx + r(0).

Свяжем с путем Г кусочно глад1<уто функцию rг:

Г t            при 0 6 t 6 r(0).

[ r(t — r(о)) _nр_Пr(0) 6 t 6 tx + r(0)

и оператор поворота.

< (Г( t)) =

J <o(y(0))             при 0 < t 6 r(0).

1 (o)(Y(t - r(0))) Пpn r(0) 6 t 6 tx + r(0).

Заменив в (3.4) Г, rг, <_t(Г(t)) их выражениями через у. r, (Y(t)) получим требуемое.

IV.    Некоторые оценки интегральных операторов

Пусть Gо- G — открытые множества, в R”. Gо С G. Рассмотрим оператор

Kf (x) = I

G

k^(x,y)f⁽У) dy,

x G G о,

(4.1)

где к: Gо x G ^ R — измеримая неотрицательная функция.

Введем

/     /1(<0(x,d))-1(y — x)|x \\ к (x,y,d ): = 1 —xl------------d------------ I 1к(x,y)

при x G Gо- y G G. d> 0.

Illklllp,»^:= sup kk(x, -,d)Lp(G)k |(x,d)|1.

x∈G₀,

0

Лемма 4.1. Пусть 1 6 p < q < ro, K — интегральный оператор (4.1) с ядром к. Тогда для x G G о

Kf (x)| 6 if- - -) q x pq

p xlllklllp,q kf |Lp (G) k1 - q M x,< (if ip)(x) q. □ (4.2)

Эта. лемма, обобщает невесовые результаты В.М. Кокилашвили, М.А. Габидзашвили [16, 17] и Б.В. Трушина. [12] в отношении вида, покрытия типа. Безиковича. и соответствующего ему вида.

∞

+ X111 k 11 p,q 1 Qx (x,di) 1 - q x i=о x ||f Lp(

6 111 k 111 p,q 1QX (x,d) 1 - 1 x x [ kf l Lp (G \

Из соображений монотонности и непрерывности при изменении d ясно, что при некотором d оба. слагаемых в квадратной скобке окажутся равными друг другу. Обозначим их общее значение через к. Возведя первое с.чагаемое в степень p — q. а второе в степень 1 и перемножив их, получим

2к = 21+1 kf | Lp(G \

Лемма 4.2. Пусть 1 6 p < q < ro, K — оператор (4.1) с ядром к. Тогда при |||k|||_p,q < го оператор K имеет ел;збый тип (p, q).               □

Доказательство следует из оценок (4.1) и (1.2).

V.    Оценки для операторов A1, A2, A3 и доказательство теоремы 2.1

Будем считать, что G G G(Л,а), так что G = = S⁰Gk. Gk G G (G, X^k ,a) hi >11 к = 1к о. Про-k = 1

извольное из открытых множеств Gk (1 6 к 6 к о) обозначим через G_о, X^k через А и рассмотрим операторы Ai: Lp(G) ^ L_q(Gо) из ('3.13') - ( .3.15 ) И = = 1, 2, 3).

Оценим сначала A3. Учитывая, что при y = Yx ix - (Y(tx) +

6 Rо + i

Доказательство. Можно считать, что kf l Lp (G) k > 0 и что правая часть (4.2) конечна. Положим ради краткости обозначений x(x,d) ^:= <(x, d)Qx(x,d)• Рассмотрим последовательность {di}₍f : d_о = d, |Q_x(x,di)| = = 2^-i | Q_x (x, d) | . Пред ставим Kf (x) в виде

Kf (x) =   У

G\<Q_a (x,d)

^k(x, У)^{f (}У) dy⁺

∞

+Х„О1 ,

x (x,di)\<Qa (x,di+1)

k^(x,y)^f(y) dy.

Применив неравенство Гёльдера. с показателями p, p0 к каждому из слагаемых правой части, получим iKf (x) | 6

6 | | | к | | | p,q | Qx (x,d) | - 11 kf| Lp (G \

|A 3 f (x) | 6 A 3 f (x) := [ xt^—x- Yf (У) i dy. R о ⁺C о

Gδ

Применяя неравенство Юнга, получаем kA3fiLq(Gо)k 6 CkfiLp(G5)k при 1 6 p < q < ro.

Оцепим Aif. i = 1,2. 3aniшем Aif в виде

(5.1)

Aif (x) = I ki(x,y)f (y) dy,

G x G G о,   i = 1,2.

Оценим |||к₁|||_p,q, считая, что s — ^pp^ + |P| > 0. Напомним. что <о = <(x,r_Y(0)). Имеем

|к 1(x, y,d)| = x(d|<- 1(x, d)(y — x)|- 1) x rY(о)                      , x у ts-1 -lX'x ( <о (y— x)lx) dt 6 о

6 Cix(d|< 1(x,d)(У - x)|^- 1) X

XX(rY(0)- 1 ^ 1(x, rY(0))(У - x) A) х rγ(0) |λ|        |λ|

X t ^- -^{1 -|A|} dt.

= C1

y_x

χ

d c2 max{rY (0), t}

)

X

X(t + r_Y)(0)⁽s 1)^p r_Y(t)^{(1 |A|})p dt.

Тогда, считая, что t_Y (t) > ct^a ,a > 1, имеем

Отсюда.

kk 1(X, ;d) iLpo (G) ||^p0 6

6 C1           I           |<- 1(x,rY(0)) X d<|^- 1(x,rY (0))( y-x) |л<Щ (0)

X (У - X) |A ^p q ^|A|)p dy =

= CI    j    |y|A^"^"A|)p0 dy 6 C2d-^P0, d<|y|x

так что

I Ik illlp., 6 C 3.

Для ядра, к₂ ny>ii 1 6 p < ro. s — |λ|

+ q^ > 0 имеем

(5.2)

4ИНШ , P⁺

|k2(x,y,d)I = X(d|^ 1(x,d)(У — x)I- 1) X tx

X Лt + rY(0))^s-1rY(t)^-|A|xf ^{|$< У}— Y⁽t)^A ) dt.

rY (t)

|||k2|||p,g 6 C2     sup    (Ip (x,d)+ Ip (x,d)), xeG 0,0

где при Tx = min{tx, rY(0)}

I₁ (x, d)^p0 =

τx

= d^p [x(^7«rV(0)⁽s^- 1+ ^)^P0 dt 6

J   V c3^rY⁽⁰⁾

6 C4rY (0) ^P0 +(s- 1+ ^)P0 + 1 6

6 C5rY(0)[^{s-|A|(1 -1)]p}0 6 C6,

0        1^1 0 ( ( d           ° (Д1-!) + ! 0

• 1₂(x, d)^p = d q ^p I x A—t\t[^s      p    1^{p 1}dt 6

τx

|λ| 0                   d              |λ| 0

• 6 C7d ^{q p} I Xy —t )t q ^p ddt 6 C8.

τx

Объединяя результаты, получаем

^|||k2^,5 < X

Применяя (в случае p > 1) неравенство Гёльдера, получаем

|k2(x, У, d)|^p0 6 X(d|<^- 1(x, d)(У — x)|- 1) X t_x

^X ^X(^rY⁽t)^- 1 ^У ^— Y⁽t) A) ^X

X (t + r_Y(0))⁽s^- 1)^p r_Y(t)⁽1^-|A|)^p dt X

при

s - a(|A| — 1) + 1 ^p

+ П > 0. ^q

(5.3)

Лемма 5.1. 1 °. Пусть s Е N, А Е [1, ro)n, min Ai = 1, 1 6 p < q < ro, s — ^P^ +    > 0.

Тогда оператор A 1 имеет слабый (p, q)-тип.

Если же при этом p > 1 ил и s — ^Р^ + ^ > 0, то оператор A 1 имеет с ильный (p, q )-тпп.

t_x

₁ ----Xr⁽t)^-1<-¹У ^— Y⁽t) A )^dt

₀rγ(t)

Учитывая свойство 6° разд. 2, имеем отсюда |k2(x, ;d)|Lp0(G)k^p0 6

t_x

p^{0 p}

.

2°. Пл"сть s Е N. А Е [1, ro)n. min Ai = 1. 1 6 а (|А| — 1) + 1      |А|

6 p < q < ro. a > 1. s--^Vl p '--+ q > 0.

G0 Е G(G,A,a). Пусть <оператор A₂ построен no Y,r_Y, удовлетворяющим требованиям 1-6 из определения 2.1.

6 C1^p0

I   IX^(rY⁽t)1 ^ЧУ ^— Y⁽t)) A^{) X}

GWQ_A (x,d) 0

X(t + r_Y(0))⁽s^- 1)^p r_Y(t)^(p-|A|)^p dtdy.

Из свойства 5° разд. 2 следует, что если

У Е <(x,d)Qа(x,d), У Е Qa(Y(t)drY (t)),

to e 1 d 6 r_Y (0) + t. Поэтому

Тогда оператор A₂ : L_p (G) ^ L_q (G0) имеет слабый (p, q)-Tiin.

а (I А| — 1) + 1 ,

Если же при этом p > 1 ил и s--p--+ + ^|А| > 0. то оператор A₂ имеет сильный (p, q)-Tiin.                                                 □

Доказательство. Из оценок (5.2), (5.3) с помощью леммы 4.2 заключаем, что каждый из операторов A 1, A₂ имеет (слабый (p, q)-тип. Отсюда, с помощью интерполяционной теоремы Марцин

Ik2(x, ;d) |Lp0 (G) k^p0 6

6 C1

t_x

χ

d c2 max{rY((0), t}

)

X

X (t + rY (0))⁽s^- 1) ^p0 rY (t)⁽p^-|A|) ^p0^{+ |A|} dt =

кевича. получаем утверждения леммы о сильном (p, q)-типе.

Доказательство теоремы 2.1. Пусть об-k о ласть G Е G (Л ,а). Тс)гла G = |J Gk. причем k=1

Gk Е G(G,Ak,a). Пл-сть f Е C^(G). При каж дом к = 1.....к о для каждого x Е Gk справедлива

оценка. (3.11). В силу оценки (5.1) и леммы 5.1 операторы Ai: Lp (G) П C~ (G) ^ Lq (Gk) it = 1,2,3) ограничены. Следовательно, при 1 6 k 6 kq для f E Ws (G) П C” (G) справедлива оценка kf iLq(Gk)k 6 c( X kDaf L(G)k + kf L(Gs)k ), |a| = s из которой следует оценка (2.1) для f E C^(G). В силу плотности C^(G) в Ws(G) оценка (2.1) остается верной для произвольных функций f с конечной правой частью (2.1).