Теоремы характеризации и обращения для обобщённого преобразования радона

При обработке экономической статистики возникает проблема, учёта, взаимного замещения производственных факторов. При производстве некоторых товаров могут использоваться ресурсы, способные заменять друг друга в производственном процессе. В работе А. А. Шананина [1] была, предложена, модель производства, (обобщённая модель чистой отрасли), в которой учитывается указанный эффект. Функция прибыли отрасли в этой модели тесно связана, с обобщённым преобразованием Радона, мер. Важность изучения свойств функции прибыли заключается в том, что наряду с производственной функцией она. является одним из основных инструментов макроописания производственных систем.

Определим на. множестве неотрицательных вещественных чисел операцию а Фа b = (аа + Ьа) “ , 0 < а 6 1.

При а = 1 это обычное сложение. На основании операции Фа определим аналог скалярного произведения для двух неотрицательных векторов р, х G R+ правилом р Өах = Р1Ж1 Фа р2х2 Фа • • • Фа РпЖп.

В экономике отображение х Н- р ®_а х называется CSS-функцией. В настоящей работе исследуется обобщённое преобразование Радона борелевских мер ц со знаком с носителем в положительном ортанте R+, которое по определению есть

_ r „ х д

^а[ц]⁽Р^,Ро) = др^ J    ^⁽dx),

РӨа^бРО где р G R+, р = 0, ро > 0 и производная понимается в смысле теории распределений. Наряду с преобразованием мер (1) в работе исследуется преобразование па[Ц](р,ро)

j (ро - р ®а х) ₊ ц(^х), ■ \

где обозначено а+ = max(0, а). Это преобразование представляет собой функцию прибыли в обобщённой модели чистой отрасли [1]. Преобразования (1) и (2) тесно связаны. Результаты, относящиеся к одному из этих преобразований, легко переносятся на другое.

Для преобразований (1), (2) в работе получены теоремы обращения и характеризации. Перед тем как переходить к этим вопросам, покажем, что в случае абсолютно непрерывных мер с непрерывными плотностями обобщённое преобразование Радона Ға[д](р,ро) есть не что иное, как интеграл от плотности по гиперповерхности уровня СҒҒ-функции.

Предложение 1.1. Пусть знакопеременная мера д нa R+ абсолютно непрерывна с непрерывной плотностью а(х). Пусть Па(р) — дифференциалъная форма на R+, удовлетворяющая равенству d$(р Өа х) Л Па(р) = dx1 Л ... Л dxn, р = 0.

Тогда для обобщённого преобразования Радона справедлива формула

■R-aM^PO)

= рӨах=ро

а(х) П_а(р),

P = 0, ро > 0.

Доказательство. Пользуясь формулой коплощади [2], запишем f а dx рӨаЖбро

Р0

=/ /

0 p®_ax=s

а(х) П_а(р) ds.

Вспоминая определение обобщённого преобразования Радона, получим

^а[д](р,ро) =        [ а(х) dx =   [ а(х)ПДр).

дро   J                J р®аЖ=8

Р0аЖ<ро

Предложение доказано.

• 2.    Характеризация

Перед тем как формулировать теоремы характеризации, дадим несколько определений, которые будут фигурировать в формулировках теорем и в их доказательствах.

Определение 2.1 [3]. Распределение Т Е F‘(0, то) называется неотрицательным (Т >  0), если для любой основной функции р Е F(0, то), р >  0 следует, что (Т, р) > 0.

Определение 2.2 [4]. Пусть Хі = (Пі, Ғі) и Х2 = (П2, ^2) ^— Д^ва измеримых пространства, /: Пі ^ П₂ ~ измеримое отображение, д — мера на Х1. Тогда мера ? на Х₂, определяемая для всех Ғ2 Е Т2 соотношением ?(Ғ₂) = д(/^—1 (Ғ2)), называется прямым образом меры д при отображении /. При этом мера д называется обратным образом меры ? при отображении /.

Определение 2.3 [5]. Функция Ғ Е С “(intR+,R) называется вполне монотонной, если для любого мультииндекса а Е Z+ имеет место неравенство

(-1)|“|

д |“|F (р) д “р

> 0

для всех р Е int R+.

Приведём здесь также две теоремы, на. которых базируется доказательство теорем характеризации.

Теорема 2.1 (о неотрицательных распределениях [3]). Пусть распределение Т Е F‘(0, то) неотрицательно: Т >  0. Тогда существует и единственна неотрицательная регулярная борелевская мера ? на (0, то), конечная на компактах и такая, что для всех р Е Ғ(0, то) имеет место равенство

∞

(Т,р) = j о

р(т ) ? (dr ).

Теорема 2.2 (Бернштейн С.Н., Gilbert V. [5]). Пусть функция F(р): R+ ^ R ограничена на R+ и вполне монотонна на int R+. Тогда найдётся такая неотрицательная конечная борелевская мера р с носителем в R+, что для всежр G R+ справедливо равенство

^F _м= j_e™ p(^dx).

R "

Наконец, перейдём к теоремам характеризации. Следующая теорема характеризует обобщённые преобразования Радона конечных неотрицательных мер с носителями в R+.

Теорема 2.3. Распределение ж(р, •) G Р‘(0, то), р G R+, р = 0 представимо в виде

$(р,ро) = ^аЫ^ро)

где р — неотрицательная конечная борелевская мера с носителем в R+, абсолютно непре рывная в нуле (т.е. р{0} = 0), тогда и только тогда, когда

• 1)    $(р, •) > 0,

• 2)    Аж(Ар, Аро) = $(р,ро) для всех А > 0,

• 3)    функция

∞ с             1

ғ(р) =    е ^(рс ,..., р^ ; т)dT ограничена на R+, вполне монотонна на int R+ и lim F(Ар) = 0 для всех р = 0. А > • “

Доказательство. Необходимость. Сначала получим формулу для действия распреде ления ж(р,ро) на основньіе функции р G Р(0, +то) Покажем, что

А'Щ, ^т),(р^(т)) = j р⁽р ^Өа ^x)P^(dx).                               (3)

В самом деле, с учётом определения производной в смысле теории распределений имеем

Мр^,т W^(t ))

—

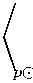
9р^(т ) дт

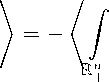
Ө(т — р Ө_а ж) p(dx),

9р^(т ) Эт

=

∞ j j Ө(т — р Өа ж) p(dx) ^dT) dT =

0 у

∞

— j j Ө(т — р Өа x) ^рТ ) dT p(dx) =

У." О

∞

=—

9р^(т ) Эт

у рөаж

dT p(dx) = J

R ++

Р(р Өа x) p(dx),

где Ө(-) — функция Хевисайда. Свойство ж(р, •) > 0 немедленно следует из формулы (3). Заметим, что распределение ж(р,ро) можно доопределить по непрерывности на функциях ф G С “(0, то) П С [0, то) с компактным носителем на [0, то). Отправляясь от случая, когда ^$(р,ро) является непрерывной функцией ро, подкорректируем формулу (3):

($(р,т ),ф(т)) = p{0N(0) +

/

ф(р Өа x) p(dx).

R ++

С учётом требования абсолютной непрерывности меры ц в нуле добавочное слагаемое исчезает. Поэтому формула (3) верна и для функций класса С “(0, то) П С [0, то) с компактным носителем на [0, то).

Для любого А > 0 имеет место очевидное равенство j    p(dx) =

(Ар)Өаж6Аро

j p(dx).

РӨаХбр о

Поэтому ш(р,ро) является положительно однородным распределением степени — 1 как производная от функции, положительно однородной степени нуль. В самом деле, для любой функции р Е Р(0, то) имеем

(ж^(АР^,АтҮрД )) = А <^⁽Ар^,т),р (А)^ =

= - А2\         ДсһДр'

\Ар)ӨаЖ<Т

А

= -Ң j ^^(dx),p(TП = ^¹$⁽р^,т ^рД )^ . ҮӨаЖбт

Свойство Аш(Ар, Аро) = ш(р,ро) доказано.

Наконец, пользуясь формулой (3) и конечностью меры ц, получаем, что

F (р) =

11    _а.

®⁽р“ ,. .. ,рп ;^т),е^-т“

)=/

R +

е-ріж“-...-рп ж“

^(dx).

Отсюда следует ограниченность, вполне монотонность функции F (р) и свойство lim F (Ар) = ц{0} = 0. Необходимость доказана.

А—+^с

Достаточность. Доказательство достаточности проведём в три шага.

Шаг 1. Из условия ш(р, •) > 0 по теореме 2.1 полу чаем, что для всех р Е R+, р = 0 существует и единственна неотрицательная борелевская мера Ц_р с носителем в (0, то), конечная на компактах в (0, то) и такая, что для любой функции р Е F(0, то) имеет место равенство

∞

^⁽ р,^т), р^(т)) = j р^(т ) pр^(dт ). о

Воспользуемся положительной однородностью распределения ш(р,ро) и вычислим при А > 0 значение

($⁽Ар^,т ),р^(тд = ^А _$ ^р, А^ ,р (А^  =

= (Х^ж (р, А^т) ,Р ( А^т )) = ^®⁽р^,т),р^(Ат )А

Пусть теперь х_п(т ) Е Р(0, то) — неубывающая последовательность основных функций такая, что х_п(т ) = 1 при т Е [^, п] и носитель х-п содержится в [ ^^, 2п]. Определим Рп(т ) = е^-т“хп(т)• Тогда по теореме Лебега о монотонной сходимости функция т ^ е^-т“ интегрируема по мере ц_р и

∞

∞

($⁽р^,т),р„^(т)) = У Рп^(т ) Pр^(dт) ^ У ^е

о

о

-

(3-

/zр(dт ) = F (Ар1 ,...,АрД.

Сделаем в интеграле замену переменных s = т“. Тогда

∞

F (Хр«,...,Хр« ) = I ■    (M*(ds},

о гДе (Др)* есть прямой образ меры др при отображении т н- т“.

Шаг 2. Из ограниченности функции F (р) нa R+ и вполне монотонности на int R+ по теореме 2.2 существует неотрицательная, конечная борелевская мера д с носителем в R+, для которой

^F .у^{е-р1 р}™ .

R++

Определим борелевскую меру v нa R+ как обратный образ меры д при отображении (xi,...,x_n) н- (x«,...,x«). Мера v конечна, так как конечна мера д. По формуле замены переменных в интеграле Лебега получим

F (р) = j е-^рі^ж?---^р"^ж“ v (dx) у

Распишем это как

F (р) =

v {0} +   у

R+\{0}

е^{-р1 ж}? ^--^-р"^ж“ v (dx).

Выберем р = Xq, q = 0 и устремим Х ^ +то. Пользуясь теоремой Лебега о монотонной сходимости и условием lim F (Xq) = 0, получаем, что v{0} = 0, то есть мера v абсолютно а > ■ ^ непрерывна в нуле.

Функция

ро ^ j v (dx)

'РӨа Жбро монотонно неубывает и ограничена. Обозначим через Vp меру Лебега-Стилтьеса, порождаемую этой функцией на [0, то), и определим распределение $о(р,ро) = ^«[v](р,ро)- Тогда для любой непрерывной и ограниченной функции р на [0, то) имеет место равенство

($о⁽р^{,т ),}Р^(т Д

∞ j р(т)vр(dт).

о

Возьмём р(т ) = е ^т “.Из формул (3), (5) следует, что

($о⁽р^{,т),е т} “) = j

R+

_е-(ріжі)“ -...-(р„ж„)“

^{v (dx)} = ^F(р« . . . ,р«).

Из необходимости следует, что $о(р,ро) есть положительно однородное распределение степени —1. Действуя, как в шаге 1 доказательства достаточности, получаем, что

F(Хр«,..., Хр«) = ($о(X¹ р,т ),е ^т “) =

∞

= ($о(р,т),е^-Ат“) = j е^-Ат“ Vр(dт).

о

Делая замену переменных s = т “и обозначая через (Dp)* прямой об раз меры D_p при таком отображении, получим, что

^

Ғ(Хр“,..., Хр“ = j e^-Xs (Dp)*(ds). о

Из конечности меры D_p следует конечность меры (D_p )*.

Шаг 3. На шагах 1 и 2 было получено, что при Х > 0

^

^

j е ^Xs (pp)*(ds) = Ғ(Хр“, ..., Хр“) = j е ^Xs (Dp)*(ds).

о

о

Перейдём к пределу при Х ^ +0. Используя теорему Лебега о монотонной сходимости, получим, что мера (цД* конечна и равенство

^

^

j е -Xs (pp)*(ds) = j е -Xs

о

о

(Dp)*(ds)

справедливо при Х > 0. Отсюда следует совпадение мер (Ц_p)* и (Dp)*. Поэтом у и меры Ц_p и Dp задающие распределения ш(р,ро) и $о(р,ро), равны. Таким образом,

$(р,Ро) = ®о(р,ро) = F_a[v ](р, ро).

Теорема полностью доказана.

Мы применим теорему 2.3 для доказательства теоремы характеризации для преобразования Па[ц](р,ро). Следующая теорема характеризует преобразование Па[ц](р,ро) в случае конечных неотрицательных абсолютно непрерывных в нуле мер с носителем в R^. Напомним, что в обобщённой модели чистой отрасли [1] преобразование Па[ц](р,ро) имеет смысл функции прибыли. Мера ц при этом имеет смысл распределения производственных мощностей по технологиям. В контексте этой модели требование абсолютной непрерывности меры ц в нуле означает отсутствие «рога изобилия» или возможности получать прибыль, не затрачивая никаких ресурсов. Поэтому требование ц{0} = 0 не является ограничительным с точки зрения экономических приложений. Перед тем как сформулировать теорему, докажем вспомогательную лемму, которая будет неоднократно использоваться в дальнейшем.

Определение 2.4 [6]. Пусть ц — знакопеременна я мера (заряд) на R+ и пусть ц = ц₊ — ц_ — разложение Жордана заряда ц. Тогда мера |ц| = ц+ + ц- называется полной вариацией заряда ц.

Лемма 2.1. Пусть ц — знакопеременная борелевская мера на R+, для которой полная вариация |ц| конечна на комп актах. Тогда при ро >  0, р Е R+ \ {0} функция П[ц](р,ро) дифференцируема по ро и справедливо равенство

Ә П“ ц';р, р,,1

= І    ц(dж).

Эро p©aX6p0

Доказательство леммы. Обозначим С(р,ро) = {ж Е R+ | р Өаж 6 ро}. Пусть А > 0. Распишем приращение п“[ц](р,ро + А) - п“[ц](р,ро) = j   (ро + А — р Өа ж) ц(dж) — j (ро — р Qa ж) ц(dж) =

G(p,po+A)                                  G(p,po)

= А j   ц(dж) + j      (ро — р Qa ж) ц(dж).

G(p,po+A)           G(p,po+A)\G(p,po)

Заметим, что

G(p,po + А) \ G(p,po) = {x € R+ | 0 < p Өа x - po 6 А} .

Поэтому справедлива оценка

(Р0 - Р Өа x) p(dx)

' (p,po+A)\G(p,po)

G(p,po+A)\G(p,po)

ІР0 - Р Өа x| |/z|(dx) 6 А

/

|/z|(dx) = о(А), А ^ +0,

G(p,po+A)\G(p,po)

так как |ц| {G(p,po + А) \ G(p,po)} ^ 0 при А ^ +0. Поэтому можно записать:

А [па[ц](р,ро + А) - na[^](p,po)] = У   ^(dx) + О(1)

G(p,po+A)

А ^ +0.

Снова пользуясь абсолютной непрерывностью интеграла Лебега, получаем

^(dx)

G(p,po +A)

→

G(p,po)

^(dx),

А ^ +0.

Случай А < 0 рассматривается аналогично. Лемма доказана.

Отметим, что в работе [5] была получена теорема характеризации для преобразования n_a[^](p,po) в случае а = 1. При а = 1 обобщённое преобразование Радона F_a[^](p,po) совпадает с классическим преобразованием Радона по гиперплоскостям. С точки зрения экономических приложений функция прибыли n_a[^](p,po) в случае а = 1 соответствует производственным системам, в которых отсутствует эффект замещения производственных факторов на микроуровне. Следующая теорема является обобщением этого результата на случай произвольных а € (0,1].

Теорема 2.4. Функция n(p,po): R+ х (0, то) ^ [0, то) представима в виде

n(p,po) = na[^](p,po), где ц — неотрицательная коне иная борелевская мера на R+, абсолютно непрерывная в нуле, тогда и только тогда, когда

• 1)    n(p,po) выпукла.

• 2)    n(Ap, Apo) = An(p, po) для всех А > 0.

• 3)    n(p, +0) = дп (p, +0) = 0 nym p € int R+

• 4)    функция

∞

• _x f _a В П. 1       1 _x

F(p) =   e    d—(pf,... ,p^ ; r)

o ограничена на R+ и вполне монотонна на int R+.

Доказательство. Необходимость. Выпуклость функции П_а [^](p, po) следует непосредственно из её определения с учётом того, что при а € (0,1] функция x ^ p Ө_а x вогнута (при а > 1 она становится выпуклой).

Положительная однородность следует немедленно из определения преобразования ЩЫ^ро):

Щ[р](Ар, Аро) = j (Аро — (Ар) Өа x)+ p(dx) = А j(ро — р Өа x)+ p(dx) = АЩ[р](р,ро).

R+

R+

В силу неравенства (ро — р Ө_а x)+ 6 ро и конечности меры р получаем, что

0 6 Па [р](р, ро) 6 ро У p(dx) ^ 0, ро ^ +0.

R+

Отсюда следует, что Па[р](р, +0) = 0.

Полвзуясв леммой 2.1, запишем эпдрДрро) дро

= ^{р {0} +}      j    p(dx).

РӨаЖбР О , ^=о

Переходя к пределу при ро ^ +0 и учитывая абсолютную непрерывность интеграла Лебега и то, что по определению абсолютной непрерывности меры р в нуле р{0} = 0, получаем ^ (р, +0) = 0.

Ограниченность и вполне монотонность функции F(р) доказывается, как в теореме 2.3, с учётом того, что д ^2^ (р, ро) = F« [р](р, ро). дро

Необходимость доказана.

Достаточность. Пусть ш(р,ро) = —^ІсусімД — производная в смысле теории распреде- ^др0

лений, то есть для всех р Е Р(0, +то) имеет место равенство

Мр^,т ^(т )) = (^п(р^,т W’^ )).

Функция на (0, +то) выпукла тогда и только тогда, когда её вторая производная является неотрицательным распределением [7]. Поэтому ш(р, •) > 0.

Так как П(р, ро) есть функция. положительно однородная степеші 1. то её вторая производная ш(р,ро) есть распределение, по.тожігте.тыю однородное степеші — 1:

амф, Ат),р(т)) = А ^ш(Ар,т),р (А)^ = А3 ^п(Ар,т),р" (А)^ =

= А2(^п(Ар, ^Ат),Р‘‘^(т)) = А < ^П(р ^,т )>Р"(^т)) = ^^1$(р^,т),Р^(т)^ .

Наконец,

⁷ а ,дИ. 1 F (р) = / е   d— ( р “

о

∞

1      11

а

, рп ; т) = е    $(ра ,..., р^ ; т) dт.

о

Как и при доказательстве теоремы 2.3, показывается, что при всех А > 0 имеет место равенство

Г -ха ,дп, 1       1

^F(Ар) = у ^{е A d}d7 ⁽р “ ,...,рп;^т)•

о

Перейдём к пределу при А ^ +то, воспользуемся теоремой Лебега о монотонной сходимости я условием д^рП (р, +0) = 0. Получим, что F(Ар) ^ 0 при А ^ +то.

Воспользуемся теперь теоремой 2.3. По этой теореме существует неотрицательная бо-релевская конечная абсолютно непрерывная в нуле мера ц с носителем на R+ такая, что $(р,Ро) = ^а[ц](р,Ро)- Определим По(р,ро) = Па [ц](р, ро). Тогда д2П(р,ро) др0

Г 1/ А    д 2П0(Р,Р0)

= ^а ^[ Ц ^]( Р, Р0) = -------- .

дрО

Из совпадения вторых производных следует, что функции П(р,ро) и По(р,ро) отличаются на полином не больше, чем первой степени по ро [7] при каждом фиксированном р. Но из равенств

П(р, +0) = По(р, +0) = 0, дд

—п(р, +0) = —по(р, +0) = 0 дро           дро следует, что этот полином нулевой. Теорема полностью доказана.

• 3.    Обращение

В случае, когда мера ц абсолютно непрерывна с плотностью a(x), будем обозначать

^аЫ^ро) := ’КДцКр^о), Щ[а](р,ро) := Па[ц](р,ро).

Кроме того, будем использовать обозначение £^p(R+,p(x)) для класса функций, принадлежащих £^P(R+) с весом p(x), то есть таких измеримых функций f (x), что

I |f (x)|^pp(x) dx <  то.

R "

Перед тем как сформулировать теорему обращения, докажем вспомогательную лемму.

Лемма 3.1. 1) Пусть П — днфференунальная форма на R+, удовлетворяющая соотношению

(dx1 + ... + dx_n) Л П = dx1 Л ... Л dx_n.

Тогда при Re z1 >  0,..., Re z_n >  0 имеет место равенство

• /        x1^1-1... ■■ п = B(z) = ^?/^z1) ... '        , z = (zi,..., z_n ).

і(^і + ... + ^zn )

жі + ...+жп=1,ж>0

• 2)    При Re ti <  1,..., Re t_n<  1 имеет место формула

  / u^-1

  R y

  
  

  . -^U-tn (1 ^{— ( u}1 ⁺ . . . ^{+ u}n) “ ^

  
  

  du — oS(1 — t)B (2, tt(u — ti — ... — tn)) ,

  
  

где t = (t1, ..., t_n), du = du1 ... du_n.

Доказательство леммы. 1) Заметим, что

/ xl1-1

R ++

xz-n-1e—E1-

^-Xn dx =

∞ j xl1-1e-X1 dx1..

∞ j x^l-1e—Xn dxn = P(zi)... T(z„).

С другой стороны,

I хф ¹. ..х«^{п 1} е ^Ж 1 '" ^Жп doc = {формула коплощади} =

R +

∞

= 7 ^е-‘    / ^Х

. . Х— ¹ Q ds = C$k = Ук8, к = 1, п} =

0      Жі+... + Жп = 5, ж>0

∞

= ^ е-sszi+...+Zn

¹ ds

у і + „+уп=1, у>0

У?

-1

...Уп ¹ Q =

= Г(щ +... + ^ у     уф^—1 ...у    Q.

уі+...+у„=1, у>0

Сопоставляя полученные выражения, получаем, что уі + ...+у„=1, у>0

Ух ¹ ...у«^{п 1} Q =

Г(^1) ... Г(г„) г(^1 + ... + z-)

= ^Ф

• 2)    Имеем цепочку преобразований

  ■ ‘1

  R +

  
  

  .

  
  

  .

  
  

  «п

  
  
  
  

  ‘п

  
  

  ^¹ - ⁽«1 ⁺ . . . ⁺ «-) ¹ ^

  
  

  du = {формула коплощади} =

  
  

  = / (1 - 8 1 ⁾      /      «Г‘‘

  0              Пі + ...+Пп = 5, п>0

  
  

  . .u_n^tn Qds = {«к = Vks, к = 1, п} =

  
  

  = / (1^{- 81})

  
  

  8«- —1—‘і —■■■-‘п

  
  

  ds

  
  

  /

  
  

  г)1 + ■■■+'Un=1, f>0

  
  
  
  

  ^Х1

  
  

  ‘ 1

  
  

  .. v—‘ⁿ Q.

  
  

Из первой части леммы следует, что v—‘1

.. v^—‘^п Q = В(1 - t1,..., 1 - t_n) =: B(1 - t).

г)1+■■■+г)n=1, f>0

Пусть у — некоторое действительное число. Вычислим интеграл s7 1 ds = |t = s« ,s = t“, ds = —t“ 1dt^ =

• ■ ■ к- ............- к-’'" ^d,=^d““^L

Поэтому

I (1 — s ¹) s^{n— 1—} ‘^1—■■■-‘^п ds = -B (2, -(п — t₁ — ... — t_n)). 0

Вторая часть леммы доказана.

Отметим, что в работе [5] была получена формула обращения для преобразования Щ[ц](р,р0) Для случая ■ = 1. Сейчас мы докажем теорему, которая обобщает этот результат на случай а € (0,1]. С точки зрения экономических приложений, следующая теорема может быть использована для нахождения распределения мощностей по технологиям по известной функции прибыли в производственных системах, в которых имеет место эффект замещения производственных факторов на микроуровне в случае, когда известно, что распределение мощностей по технологиям является абсолютно непрерывным.

Теорема 3.1 (3.1.’). Пусть

а(х) € Г1 (R+ ,х“(с1-1)

.

а(с„-1)) _п л2 Ато п   2а⁽С1^-1)+1     2а(с„-1)+1)

. . ^Х п^                 J I I -"*'-' I -Ll^ । , ^х 1                          . . . ^х п^                          J при некоторых действительных с1 < 1,... ,сп < 1. Тогда

a(x) = j К_а(р1Х1,... ,рпХп; с)Щ[а](р, 1) dp,

R +

/              1 t                                                  \

I a(x) = III К_а(р₁х₁,... ,р_пх_п ; с)^_а[а](р, s) ds dt dp I ,

R " G G где ядро Ка есть а 2п-1 К(u; с) = ^

“v ’    (2лг)п

lim /

R -х

-a(zi-1)-1     -аХп

U1             . . .Un

1) ^z

B⁽¹ — Z1,..., ¹ — Zn)B ^(2, a⁽n — Z1 ^— ... — Zn))

c+tB"(G,R)

с = (ci,... ,cn), a Bn(0, R) есть шар e Rn радиуса R с центром в начале координат.

Доказательство. Для сокращения обозначений положим П(р,ро) = Щ[а](р, ро). По определению

П(р,ро) = J (ро - ((P1X1)“ + ... + (рпХп)“)“ )₊ a(x) dx.

Сделаем замену yk = x^, k = 1,n. Якобиан за мены равен ^|j = а ⁿ(x1. ..x_n)¹ “. Обозначив a*(x“, ..., x“) = а^-па(х₁,..., x_n)(x₁... x_n)^1-“, получим

ⁿ⁽P,PG)=    (pg ^{— (} р “ У 1 ⁺ ... ⁺ P“yn) ¹) ^a*⁽y) ^dy.

R +

Пользуясь этой формулой и теоремой Фубини, придём к следующему выражению:

..

. ,Рп ;1) dp =

= j a*(y) j p-¹ ...p-" (1 - (р1У1 + ... + рпУп) ¹)₊ dpdy = ^u_k = pk yk ,k = 1,n} =

R ++

R "

/ tl — 1     tn

У11   ... Уп"

у

R ++

Из последней формулы видно, что по функции П(р,ро) можно получить преобразование Меллина функции a*(x). На этом и основана формула обращения.

Из леммы 3.1 следует, что при Re t1 <  1,..., Re t_n<  1 имеет место формула

/ P^-1 ...P^-" П(Р1 , R "

..

. ,Рп ;1)dp =

= ^{aB(1 — t)B} 22,а (п ^— £ nA ) J y1^{1 1} . ..уП "

\    \ k =1   / / R +

1a*(y)dy.

Пусть т = (т,..., т—) G R^-. Докажем следующую формулу для преобразования Фурье:

Г (а* (е^ж1 ..,• )exp(c • x))(т ) = J yt^{1 +c1-1} ... y ' а . y ,..., y dy. (7) R y

Имеем следующую цепочку преобразований:

Г (а* (еж1,..., еж") ехр(щжі + ... + c-x-)) (т) = j exp (г(x1т1 + ... + хпТп) + c1x1 + ... + cnxn) а* (еж1,..., еж") dx = R"

= У_Ук = е^Жк , xk = ln yk , dxk = y-^dyk к = 1,n} =

= У уД ^+C1-1 ... ,y           -a y ,..., y dy.

R y

Учтём при этом, что j exp (c1x1 + ... + cnxn) |а* (еЖ1,..., еж")| dx =

R "

= У y^¹.. .yk ¹ K(y1,... ,y„)| dy = {yk = u^, dyk = au£^-1duk , к = 1,n} = R y

= j u“^{(c1 1)} . ..u“^(c" ^-1)|а(u₁ , . ..,u_n)| du <  to

Ry в силу условия теоремы. Аналогично

У exp (2(c₁x₁ + ... + c_nx_ny) |а* (е^Ж1 ,..., е^ж" )|² dx = R "

= У y2^c1-1.. .yn^cn-1|a*⁽y1,... ,y»^{)|2 d}y =

R y

= a^-n У u1“^{(c1 1)+1} ... u²“(^Cn-1)+1|a(u₁,... , u_n)|² du <  to .

R y

Таким образом, exp (c1x1 + ... + cnxn) а* (е61,..., еж") G £1(Rn) П £2(Rn).

Отсюда следует, что преобразование Фурье (7) существует и по теореме Планшереля [8] принадлежит £2 (Rn).

Учитывая (6) и (7), получаем, что

Г (а* (е^ж1 ,..., е^ж" ) exp(c1x1 + ... + c_nx_n)) (т ) =

1                      .

=

R y

________ P- ^{1 1} ...p^-" ^c" n(pf ,...,p^ ; 1) dp ________ aB(1 — c — гт)B (2, an — a(c₁ + гт₁ + ... + c_n + гт_п))

Возьмём обратное преобразование Фурье от левой и правой частей. Из принадлежности функции классу £2(Rn) следует, что обратное преобразование Фурье может быть вычислено по формуле [8]:

а* (еЖ1,..., еж") exp(cim + ... + с„х„) =

—       1

1 _r f f exp(—гх • т )р— ^{1 1} ...р_п^гт" ^с" П(р f, ...,р” ; 1) dp

-^{im                                                             dT}

(2тт)^п R^^ J J аВ (1 — с — гт )В (2, ап — а(сі + гт₁ + ... + с„ + гт_п)) B(0,R) ■"

Обозначим yk = e^$k, к = 1,п. Формула перепишется в виде

а*(у1, ...,уп) = lim

(2^)ⁿ R^^

B(0,R) У

(ріУі)-іт1-с1 ... ру           П(рі— ,...,р” ; 1) dp dT.

аВ (1 — с — гт)В (2, ап — а(с₁ + гт₁ + ... + с_п + гт_п))

Теперь обозначим у к = х^ и сделаем заме ну переменных рк = q^, к = 1,п. Возвращаясь от функции а*(-) к фуіікпіш а(-). получим

а(х) =

а2”-1 _. Г Г q х             -1)-1... q х                     n(qi, ...,q„;1) dq , щтщщ „-im        -----ғдд------■ ч^-------7——.—;----;---- ■   ---dт■

(2^)ⁿ R^^  J J     аВ(1 — с — гт )В (2, ап — а(с₁ + гт₁ + ... + с^ + гт_п))

B(0,R) ■+

Делая замену переменных zk = ск + гт^, к = 1,п и пользуясь определением ядра К_а(п; с) в условии теоремы, получаем требуемую формулу обращения для преобразования П_а[а](р,р₀). Формула обращения для преобразования ^_а[а](р,р₀) непосредственно следует из равенств

Э 2^п_а^[а](р^,р0⁾ _

п 2          ^а[а](р,р0), др0

Па[а](р, +0) =    “[а] (р, +0) = 0, р G int R”, которые влекут Па[а](р,р0) = j"^0 J0 ^.а[а](р, s) dsdt. Покажем, что равенства (8) - (9) действительно имеют место.

Равенство (8) следует из леммы 2.1 и определения преобразования ^а[а](р,р0).

Далее для любого р G int R+ найдутся такие В(р') >  0 и р* (р), что

Щ[а](р,р0)

= I     ( р 0

R+nBn(0,R(p))

— р Ө_а х)₊а(х) dx

при 0 < р0 < р0(р) Запишем

0 6 |П_а[а](р,р0)| 6 j     (р0 — р Ө_ах)₊|а(х)| dx 6

R+nB"(0,R(p))

6 р0

J     |а(х) | dx 6 Ср0     J

х“^(с1 ¹⁾ ... х^⁰" ¹⁾ |а(х) | dx 6

R+nBn(0,R(p))

■ '.   B' (0,R.q

^{6 Ср}0 ||^а(х) |І£1 ( r „ ^a(c1^-1) _s^f(c_n^-1)) ,

где С >  0 — некоторая постоянная. Переходя к пределу при р0 ^ +0. получаем, что Щ[а](р, +0) = 0.

Теперь воспользуемся леммой 2.1 и запишем:

0 6

Э П_а[а](р,ро) Эро

j |а⁽ж^)|

dx 6

рӨаж6ро

6 j      |°(x)| dx 6 C₂      I      x“^(c1 1)

. .x“^(c" ¹⁾|a(x)| dx,

R +nB-(O,Cipo)                   R +nB-(O,Cipo)

где Ci > 0, C2 > 0 — некоторые константы. Из принадлежности x“(c1-1) . ..x“(c"-1)a(x) G Г1 (R+)

следует, что имеет место стремление

Х“(с1-1)

. .x“^(c" ¹⁾|a(x)| dx ^ 0,

ро ^ +0.

R +nB"(O,C2po)

Это доказывает, что ^"^pd"] (p, +0) = 0- Таким образом, доказаны равенства (9), а вместе с ними и теорема.

Работа поддержана Министерством образования и науки Российской Федерации, соглашение №14.А18.21.08бб.