Теоремы о сохранении орбитального углового момента суперпозиций смещённых оптических вихрей

Лазерные пучки с орбитальным угловым моментом (ОУМ) нашли применение в манипуляции микрообъектами, квантовых телекоммуникациях, микроскопии, интерферометрии, метрологии. Недавний обзор работ по ОУМ приведён в [1]. В [2] впервые было показано, что моды Лагерра–Гаусса обладают ОУМ. Среди пучков, обладающих ОУМ, известны также пучки Бесселя, способные распространяться без дифракции. В некоторых работах были получены аналитические выражения для плотности ОУМ для пучков Бесселя [3–5]. Недавно были рассмотрены непараксиальные асимметричные моды Бесселя [6], для которых также было получено аналитическое выражение для ОУМ всего пучка. Суперпозиция несмещённых вихревых лазерных пучков, в частности Бесселевых пучков, рассматривалась ранеее в [5, 7–10], в [11] рассматривался ОУМ суперпозиции вихревых лазерных пучков с периодическим смещением. В работе [12] рассматривается формирование параксиальных световых пучков различной формы с заданным значением орбитального углового момента.

В данной работе рассматривается суперпозиция произвольных одинаковых радиально-симметричных оптических вихрей (в том числе непараксиальных), каждый из которых смещён на произвольный вектор в плоскости, поперечной оптической оси. Доказываются две теоремы. Первая теорема утверждает, что если весовые коэффициенты суперпозиции вещественны (т.е. разность фаз между пучками в суперпозиции равна 0 или п ), то нормированный ОУМ (точнее проекция ОУМ на оптическую ось) всей суперпозиции равен нормированному ОУМ каждого входящего в неё пучка. Вторая теорема утверждает, что для со-

С. 305-310.

хранения нормированного ОУМ коэффициенты суперпозиции могут и не быть вещественными, но тогда центры всех вихрей должны находиться на одной прямой, проходящей через начало координат (точку, относительно которой рассчитывается ОУМ). Численный расчёт ОУМ для суперпозиций трёх и пяти оптических вихрей разной формы подтверждает утверждения обеих теорем.

• 1.    Орбитальный угловой момент суперпозиций одинаковых оптических вихрей с радиальной симметрией

Хорошо известно, что любое решение непараксиального уравнения Гельмгольца может быть представлено как суперпозиция плоских волн:

E ( r , ф , z ) = jj A ( р , 6 ) х

^{ℝ 2}                                            (1)

х exp [ ikr р cos (6 - ф) + ikz J1 -р2 ] р d р d 6, где к = 2лА - волновое число света с длиной волны %, E – комплексная амплитуда поля в цилиндрических координатах (р, ф, z), A - угловой спектр в полярных координатах (р, 9). В параксиальном приближении вместо корня (1 -р2)1/2 в показателе экспоненты будет (1 - р2/2).

Если исходный пучок смещён на вектор с декартовыми координатами ( x 0 , y 0 ), то его угловой спектр плоских волн имеет вид:

A '( р , 6 ) = A ( р , 6 ) exp [- ik р ( x ₀ cos 6 + y ₀ sin 6 ) ] , (2)

где A(р, 9) - угловой спектр плоских волн исходного (несмещённого) пучка. ОУМ и мощность пучка могут быть рассчитаны как через комплексную амплитуду, так и через угловой спектр плоских волн. Можно показать, что проекция ОУМ на оптическую ось Jz и мощность лазерного пучка I вычисляются с помощью соотношений:

^

S pq = kCC J| D ( p )|² p ² d px

—_z =- i[[E* ^^rdrd ф = - i %² [[ a* —p d p d 6 , ^J_t^J2     ^дф                 » 2     ^d6

I = JJ E * Erdrd ф = % ² JJ A * A p d p d 6 .

ℝ ²

ℝ ²

Нормированный ОУМ (ОУМ на фотон) получается как отношение J z / I .

Пусть угловой спектр плоских волн вихревого лазерного пучка имеет вид:

A ( p , 6 ) = D ( p ) exp ( in 6 ) ,

где D ( ρ ) – произвольная, в общем случае комплекснозначная функция, n – целочисленный топологический заряд. Тогда комплексная амплитуда такого вихревого пучка будет иметь вид:

E ( r , ф , z ) = JJ D ( p ) exp ( in 6 ) x

ℝ ²

X exp [ ikr p cos ( 6 - ф ) + ikzJ 1 -p ² ] p d p d 6 =

= 2 п i n exp ( in ф ) х

^

х J D ( p ) exp ( ikz-J 1 -p ² ) —_n ( kr p ) p d p =

= B ( r , z ) exp ( in ф ) .

А в начальной плоскости комплексная амплитуда будет иметь вид, аналогичный (5):

E ( r , ф , z = 0 ) = B ( r , z = 0 ) exp ( in ф ) = = B ( r ) exp ( in ф ) .

Рассмотрим суперпозицию M одинаковых оптических вихрей (7) с весовыми коэффициентами C m , причём каждый пучок смещён в декартовой плоскости на вектор с координатами ( x m , y m ), m = 0, ..., M – 1. Угловой спектр плоских волн всей суперпозиции равен

A ( p , 6 ) = D ( p ) exp ( in 6 ) X

M -1

X E Cm exp [-ikp( xm cos 6 + Ут sin 6)} m=0

Подставив (8) в (4), вычислим мощность такого пучка:

M -1 M -1      ^

I = % ² EE C ^ C q J| D ( p )| p d pX p =0 q =0         0

2п

X J exp [ ik p ( a_pq cos 6 + b_pq sin 6 ) J d 6 , 0

где a_pq = x_p – x_q , b_pq = y_p – y_q .

Аналогично вычислим ОУМ (3):

M -1 M -1

—z = nl + %2 EE Spq , p=0 q=0

где

2п

X J ( x q sin 6- y q cos 6 ) x

X exp [ ik p ( a_pq cos 6 + b_pq sin 6 ) J d 6 .

Поделив ОУМ на мощность пучка, получим выражение для нормированного ОУМ:

у         Л 2 M -1 M -1

-z = n + — уy s .

pq

I I p =0 q =0

Сначала в двойной сумме в (12) вычислим диагональные слагаемые (т.е. при p = q )

^

^Spp = ^k C P Г JI D H ² P 2 ^d P^X

2п

X J ( x p sin 6- y p cos 6 ) d 6 = 0.

Внедиагональные слагаемые входят в двойную сумму в (12) попарно, вычислим сумму двух симметричных слагаемых:

^Spq ^{+ S}qp

M

2п

= ^kCP C q JI ^D ( p )|² P ² d P J ( x q sin ^6- y q cos ⁶ ) ^X

X exp [ ik p ( a_pq cos 6 + b_pq sin 9 ) ] d 6 +

^

2п

^{+ k} C p C q JI ^D ( p )|² p ^{2 d} p J ( x p ^{sin 6-} y p ^{cos 6} ) ^X 00

X exp [ ik p ( - a_pq cos 6- b_pq sin 6 ) J d 6.

Во втором интеграле сделаем замену 9 ^ 9 + п , но пределы интегрирования оставим прежними, так как производится интегрирование периодической функции по всему периоду. Тогда показатели экспонент в обоих интегралах станут одинаковыми и выражение (14) примет вид: ^

^Spq ^{+ S}qp = ^k J| ^D ( p^p ^{2 d} p^X

x ' j [ ( C p C q y p - C ; C.y. ) cos ⁶- 0

- ( C p C q X p - C p C q X q ) sin 6] X

X exp [ ik p ( a_pq cos 6 + b_pq sin 9 ) ] d 6 .

Если все весовые коэффициенты суперпозиции (8) вещественны (т.е. разность фаз между пучками в суперпозиции равна 0 или п ), то подынтегральное выражение можно представить в виде полного дифференциала по переменной 9 от экспоненты, т.е.

^

S pq + S qp =- iC p C q J| D ( p )|² A d pX

X exp [ ik p ( a_pq cos 6 + b_pq sin

6=2п

= 0,

16=0

поэтому второе слагаемое в (12) равно нулю. Таким образом, мы доказали следующую теорему.

Теорема 1. Пусть имеется световой пучок, являющийся суперпозицией смещённых с оптической оси одинаковых оптических вихрей с произвольной радиальной формой и топологическим зарядом n , причём все весовые коэффициенты суперпозиции вещественны, а смещение каждого пучка может быть произвольным. Тогда нормированный ОУМ всей суперпозиции равен ОУМ одного пучка J_z / I = n .

Как частный случай из теоремы следует, что смещение одиночного пучка в поперечной плоско-

2. Численное моделирование

Проверка утверждений обеих теорем осуществлялась путём численного моделирования. Были рассмотрены четыре различных вида оптических вихрей с топологическим зарядом n : бездифракционные моды Бесселя [13], непараксиальные пучки Ханкеля– Бесселя [14], параксиальные пучки Бесселя–Гаусса [15] и параксиальные моды Лагерра–Гаусса [2]. Комплексная амплитуда пучка Бесселя в начальной плоскости имеет вид [13]:

E i (r , ф , z = 0) = J n ( a r ) exp ( in ф ) ,                 (21)

сти не приводит к изменению его нормированного ОУМ [11].

Если же коэффициенты в суперпозиции (8) комплексны, то для вычисления нормированного ОУМ

можно воспользоваться следующим интегралом:

2п

J exp ( ia cos 6 + ib sin 6 )

cos 6

sin 6

d 6 =

i 2n г2 + b2

Тогда из (15) вместо (16) получим:

2 n ik

^Spq ^{+ S}qp         '

R pq

x[(с C*y -С*C у Mx —x

L\ p qyp     p q^yq )\^p q /

- ( ^^ ^XP - ^CP^Cq^Xq )( У р - y q ) ] ^X

^

^X J ^D ( Pf ^J 1 ( R P ) P ^{2 d} P ^, 0

где R pq = [( x p – x q )²+( y p – y q )²]^1/2 – расстояние между центрами p -го и q -го вихрей. Для того, чтобы сумма (18) была равна нулю, необходимо, чтобы выполня-

лось следующее условие:

C p C q [ y p ⁽ x p - x q ) " x p ⁽ y p - У ) ] =

= ^C ^ C q ^[ у , ( x p — x q ) - ^Xq ( Ур - у , ) ^] ,

которое после сокращений в квадратных скобках приводится к виду:

**

p q p y q    q y p      p q p y q    q y p .

Если коэффициенты C_p и C_q невещественные, то условие (20) выполняется только при равенстве нулю выражений в скобках. Таким образом, мы доказали следующую теорему.

Теорема 2. Пусть имеется световой пучок, являющийся суперпозицией M смещённых с оптической оси одинаковых оптических вихрей с произвольной радиальной формой и топологическим зарядом n , причём центры всех оптических вихрей ( x_p , y_p ) ( p = 0, ..., M – 1) в суперпозиции находятся на одной прямой, проходящей через начало координат (т.е. x_py_q = x_qy_p для любых p и q ). Тогда нормированный ОУМ всей суперпозиции равен ОУМ одного пучка J_z / I = n .

где а - масштабирующий множитель. Комплексная амплитуда пучка Ханкеля–Бесселя в начальной плоскости равна [14]:

E 2 ( r , ф , z = 0) = H ^’ Г kr ) Jn, 2 Г kr 1 exp ( in ф ) , (22)

где k – волновое число света. Комплексная амплитуда пучка Бесселя–Гаусса в начальной плоскости имеет вид [15]:

Г r ²        )

E 3 ( r , ф , z = 0) = J_n ( a r ) exp I--2 + in ф I , ( w         I

где а - масштабирующий множитель, w - радиус перетяжки Гауссова пучка. Комплексная амплитуда пучка Лагерра–Гаусса в начальной плоскости равна [2]:

n

_ ,                I r V2 |

E 4< r , ф , z = 0) = ---- X

w

22 rr X L m \ —у I exp | t + in ф I , I ^w ) I w )

где m – порядок моды, w – радиус перетяжки Гауссова пучка, Lⁿ_m ( x ) - полином Лагерра.

На рис. 1 показаны интенсивности и фазы суперпозиций из трёх пучков, центры которых находятся в вершинах правильного треугольника. Все пучки в суперпозициях имеют топологический заряд n =7. Рис. 1 был рассчитан по формулам (21)–(24) с числом отсчётов 1000× 1000. Параметры пучков были подобраны таким образом, чтобы световой треугольник на всех дифракционных картинах имел примерно одинаковые размеры. Нормированный ОУМ всех четырёх пучков был рассчитан по формулам (3), (4) и оказался равен J z / I = 7 , несмотря на различие дифракционных картин. Аналогично на рис.2 показаны интенсивности и фазы суперпозиций из пяти таких же пучков, но расположенных в вершинах правильного пятиугольника (большего размера). Нормированный ОУМ всех пучков на рис.2 также был рассчитан по формулам (3), (4) и также оказался равен J z / I = 7 .

На рис. 3 а,б показаны интенсивность и фаза суперпозиции из пяти мод Лагерра–Гаусса порядка ( n , m ) = (7, 2), расположенных на прямой y = 0,4 x в точках с координатами x_m = [-12, -6, 0, 6, 12] % , y_m = 0,4 x_m , m = 0, ..., 4, с параметрами % = 532 нм, w = % , вектор весовых коэффициентов C m = exp(2 n im /5), размер расчётной области 2 R = 40 % (т.е. - R < x , y < R ).

в)

д)

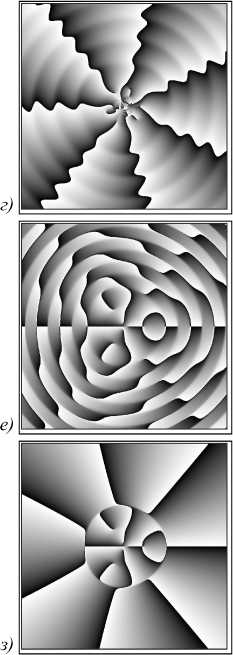
Рис. 1. Интенсивность (негатив) (а, в, д, ж) и фаза (чёрный цвет – π , белый цвет – - π ) (б, г, е, з) суперпозиций трёх вихревых пучков (длина волны λ = 532 нм), расположенных в вершинах правильного треугольника в точках с координатами x_p = R₀cos ϕ _p, y_p = R₀sin ϕ _p (R₀ = 0,3 λ , ϕ _p = 2 π p/3, p = 0, 1, 2) и имеющих топологический заряд, равный 7: мод Бесселя (а, б), пучков Ханкеля–Бесселя (в, г), пучков Бесселя–Гаусса (д, е) и пучков Лагерра–Гаусса (ж, з). Вектор весовых коэффициентов в каждой суперпозиции равен

C = (1, 1, 1), размер расчётной области 2R = 10 λ . Масштабирующий множитель пучков Бесселя и Бесселя–Гаусса (а, б, д, е) α = 6/ λ . Радиус п ер етяжки Гауссова пучка равен w = 2 λ (д, е) и w = λ (ж, з).

Индекс моды Лагерра–Гаусса (ж, з): (n, m) = (7, 1)

б)

На рис. 3 в,г показаны интенсивность и фаза суперпозиции из пяти пучков Бесселя–Гаусса 7-го порядка, расположенных в тех же точках, что и на рис. 3 а,б (т.е. на прямой y = 0,4 x в точках с координатами x m = [-12, -6, 0, 6, 12] λ , y m = 0,4 x m , m =0, ..., 4), с параметрами λ =532 нм, w =2 λ , α = 2/ λ , вектор весовых коэффициентов C m = exp(2 π im /5), размер расчётной области 2 R =40 λ (т.е. – R ≤ x , y ≤ R ).

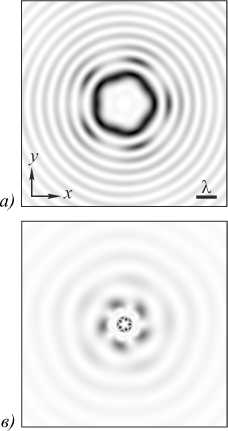
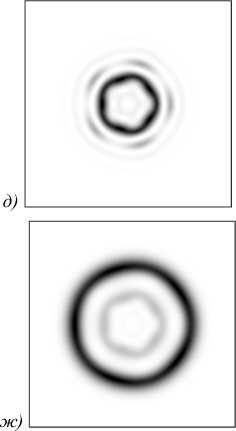
Рис. 2. Интенсивность (негатив) (а, в, д, ж) и фаза (чёрный цвет – π , белый цвет – - π ) (б, г, е, з) суперпозиций пяти вихревых пучков (длина волны λ = 532 нм), расположенных в вершинах правильного пятиугольника в точках с координатами x_p = R₀cos ϕ _p, y_p = R₀sin ϕ _p (R₀ = 0,5 λ , ϕ _p = 2 π p/5, p = 0, ..., 4) и имеющих топологический заряд, равный 7: мод Бесселя (а, б), пучков Ханкеля–Бесселя (в, г), пучков Бесселя–Гаусса (д, е) и пучков Лагерра–Гаусса (ж, з). Вектор весовых коэффициентов в каждой суперпозиции равен C = (1, 1, 1, 1, 1), размер расчётной области 2R = 10 λ . Масштабирующий множитель пучков Бесселя и Бесселя–

Гаусса (а, б, д, е) α = 6/ λ . Радиус перетяжки Гауссова пучка равен w = 2 λ (д, е) и w = λ (ж, з). Индекс моды Лагерра–Гаусса (ж, з): (n, m) = (7, 1)

б)

Нормированный ОУМ обоих пучков на рис. 3 также был рассчитан по формулам (3), (4) и также оказался равен J_z II ≅ 7.

Заключение

Таким образом, в данной работе рассмотрен ОУМ суперпозиции одинаковых радиально-симметричных оптических вихрей, каждый из которых смещён в плоскости, поперечной оптической оси.

б)

а)

• г)

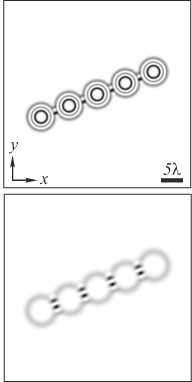
Рис. 3. Интенсивность (негатив) (а, в) и фаза (чёрный цвет – π , белый цвет – - π ) (б, д) суперпозиции пяти мод Лагерра– Гаусса (а, б) и пучков Бесселя–Гаусса (в, г). Параметры мод Лагерра–Гаусса: порядок (n, m) = (7, 2), радиус перетяжки w = λ . Параметры пучков Бесселя–Гаусса: порядок n = 7, радиус перетяжки w = 2 λ , масштабирующий множитель α = 2/ λ . Все пучки имеют длину волны λ = 532 нм, центры расположены на прямой y = 0,4x в точках с координатами x_m = [-12, -6, 0, 6, 12] λ , y_m = 0,4x_m, m = 0, ..., 4, вектор весовых коэффициентов в суперпозиции C_m = exp(2 π im/5), размер расчётной области 2R = 40 λ

Доказано две теоремы о сохранении нормированного ОУМ такой суперпозиции. Если весовые коэффициенты суперпозиции вещественны (т.е. разность фаз между пучками равна 0 или π ), то независимо от смещения пучков нормированный ОУМ всей суперпозиции равен нормированному ОУМ каждого входящего в неё пучка, т.е. его топологическому заряду. Если центры пучков расположены на одной прямой, проходящей через начало координат (точку, относительно которой рассчитывается ОУМ), то даже при комплексных весовых коэффициентах нормированный ОУМ всей суперпозиции также равен нормированному ОУМ каждого входящего в неё пучка.

Проведено численное моделирование , подтвердившее сохранение нормированного ОУМ для суперпозиций трёх и пяти оптических вихрей разной формы. Доказанные теоремы позволяют с помощью любого числа одинаковых радиально-симметричных вихревых пучков путём подбора весовых коэффициентов и величины смещения каждого пучка с оптической оси формировать новые пучки с разным распределением интенсивности (в том числе и не радиально-симметричным), но обладающие одинаковым нормированным ОУМ .

Работа выполнена при поддержке Министерства образования и науки РФ, а также грантов РФФИ 14-2907133, 15-07-01174, 15-47-02492 и 15-37-20723.