Теоретическая модель диссоциации четырехкислотных оснований при совместной нейтрализации аминогрупп и ее приложение для определения констант диссоциации РК1,2,3,4
Автор: Танганов Б.б, Кузнецова О.С., Багаева Т.В., Крупенникова В.Е.
Журнал: Вестник Восточно-Сибирского государственного университета технологий и управления @vestnik-esstu
Рубрика: Естественные науки
Статья в выпуске: 2 (25), 2009 года.
Бесплатный доступ
Разработана методика определения констант диссоциации протонированных четырехкислотных оснований, отличающаяся новым подходом к оценке и учету концентраций всех равновесных частиц в процессе нейтрализации полиоснования.
Диссоциация, нейтрализация, кислотно-основное равновесие, протонирование
Короткий адрес: https://sciup.org/142148264
IDR: 142148264 | УДК: 541.132:547.415
Текст научной статьи Теоретическая модель диссоциации четырехкислотных оснований при совместной нейтрализации аминогрупп и ее приложение для определения констант диссоциации РК1,2,3,4
Термодинамические константы диссоциации протонированного основания определяются следующими соотношениями [1,2]:
|
Ka 1 = a + a 1 H + |
• [ B ] • f 0 K = a • [ BH + ] • f 1 [ bh +] • f/ a 2 H + [ bh 22 + ] • f 2’ (1) |
|
Ka 3 = а + а з н + |
[ BH 22 + ] • f 2 K = a [ BH 33 + ] • f 3 [ BH 3 ] • f , ’ a 4 H + [ BH 4- ] • f 4 |
В уравнении (1) a - активность ионов лиония - сольватированного иона водорода в H + любой точке потенциометрического титрования; [B],[BH + ],[BH22 ],[BH33+ ],[BH4+ ] - равновесные концентрации нейтрального и протонированного четырехкислотного основания в процессе титрования сильной кислотой; f0, f1, f2, f3, f4 - коэффициенты активности нейтральной и протонированных форм полиоснования.
Как отмечалось ранее [2,3], известные методы оценок ионной силы при кислотноосновном равновесии [4,5,6,7] основаны на использовании концентрации первой ионизированной частицы, например, [ВH+] для двухкислотного основания. Было показано [1,3,8,9], что в расчетах констант диссоциации не следует пренебрегать равновесными концентрациями остальных ионов, так как их величины в различных точках титрования сопоставимы с концентрацией первого протонированного иона, а из данных таблицы 2 и рисунка 1 видно, что в процессе протонирования концентрации последующих ионов (например, даже [BH4 ]) превышают таковые иона [ВH+].
Наиболее приемлемым способом оценки ионной силы, определяемой с учетом равновесных концентраций всех заряженных частиц, является представление кривой титрования основания в логарифмических координатах [1,2,3,9]. При этом равновесные концентрации всех частиц [ B ],[ BH + ],[ BH 2 ' ],[ BH 3 3 + ],[ BH 4 ], образующихся при титровании четырехкислотного основания сильной одноосновной хлорной кислотой, могут быть определены на диаграммах - lg a + - lg C . Оценка значений коэффициентов активности fo , f, f2, fs и f прово-
H+ дится по более оптимальному методу Дэвиса [6]:
lg f-=-AM^ + 0.1-1 (2)
1+и
Измерения ЭДС и потенциометрическое титрование в среде диметилформамида (ДМФ ) осуществляли при 25.0 ± 0.2 0 С на рН-метре-милливольтметре METROHM-632 (Швейцария). Растворитель очищен и обезвожен по известным методикам [10,11]. Содержание воды, определенное модифицированным методом К.Фишера [12], не превышало для ДМФ ± 0.02 мас.%.
В таблице 1 приведены данные измерения ЭДС цепи (I)
Стеклянный электрод/HClO 4 /AgCl,Ag (I)
в среде ДМФ в зависимости от моляльной концентрации хлорной кислоты, а также результаты оценки степени диссоциации HClО 4 и исходные величины для расчета стандартного потенциала цепи.
Степень диссоциации хлорной кислоты может быть оценена по уравнению (3) [1,2.3,9,13].
lg(1 - a ) = ( E О - Е изм + 0.059 lg m ) / 0.059 (3)
Величина Е 0 , равная разности E 0 - 0.059p K а ( HClO 4) = E 0 ( 0 = 2.3 - RT / F ), определена по программе « Выполнение расчета нормального потенциала цепи без переноса Е * » по зависимости Еизм = f (lg m ) при lg m = 0. Получена величина Е 0 = 0.3791 с коэффициентом регрессии r = 0.9895.
Таблица 1
Изменение ЭДС цепи (I) в зависимости от моляльной концентрации хлорной кислоты (m, моль HClO 4 /1000г ДМФ) и данные для определения Е 0 цепи (I)
|
m |
E , B |
α (HClO 4 ) |
|
0.1371 |
0.340 |
0.3694 |
|
0.06855 |
0.330 |
0.5342 |
|
0.03427 |
0.320 |
0.6559 |
|
0.01713 |
0.309 |
0.7358 |
|
0.008565 |
0.295 |
0.7719 |
|
0.004282 |
0.275 |
0.7511 |
|
-0.0581 - lg ( ma ) |
( m - a ) 0'5 |
E’ |
|
1.2954 |
0.2250 |
0.4164 |
|
1.4363 |
0.1913 |
0.4147 |
|
1.6482 |
0.1499 |
0.4172 |
|
1.8995 |
0.1123 |
0.4211 |
|
2.1797 |
0.0813 |
0.4236 |
|
2.4927 |
0.0567 |
0.4221 |
Значение стандартного потенциала цепи (I) определено по авторской компьютерной программе «Расчет параболической функции y = a0-xn + a1 - xn"1 + ... + an для определения стандартных потенциалов Е 0 (стандартных ЭДС) электрохимических цепей » по приближению функции E ' = f ( m a ) 0.5 при ( m a ) = 0, где E ' = Еизм + 0.059lg( m a ).
E ' = 0.1379 - ( m a ) - 0.088 - ( m a )05 + 0.4272 , r = 0.9090.
Таким образом, получена величина стандартного потенциала цепи (I) в среде ДМФ , равная Е о = 0.4272 В .
Стандартный потенциал цепи (I), наряду с равновесными концентрациями нейтральной молекулы основания и заряженных частиц [B],[BH + ],[BH22+ ],[BH33+ ], [BH0+ ], образующихся в процессе титрования основания, оцененных по таблице 2 и рисунку 1, и их коэффи- циентами активностей f0, f1, f2, f3 и f4 дают возможность определения термодинамических констант кислотности протонированных полиоснований в среде органических растворителей.
Оценка активности лионий-ионов в процессе титрования основания возможна по уравнению Нернста:
- 1g a + = ( E о — Е изм )/0.0595.
H
Рассматриваемая методика, отличающаяся от известных применением логарифмических зависимостей при оценке ионной силы и коэффициентов активности ионов, как отмечалось в [2], была апробирована на примере 1,3-дифенилгуанидина ( ДФГ ) в среде ДМФ . В литературе [14] известна величина рК а ( ДФГ/ДМФ ) = 9.1. Нами было [1] получено значение рК а (ДФГ/ДМФ ) = 9.15 ± 0.03, свидетельствующее о достаточной надежности и воспроизводимости предлагаемого метода.
Таблица 2
Расчет констант диссоциации протонированного 3,3’4,4’-тетрааминодифенилоксида в среде ДМФ по ур.(1) и (2)
|
V , мл 0.3 |
E , B 0.040 |
-lg a H + 6.5593 |
[ B ] 0.05652 |
[ BH + ] 0.03183 |
[ BH 22+ ] 0.00460 |
[ BH 33+ ] 0.00071 |
[ BH 44+ ] 0.00013 |
|
|
0.5 |
0.043 |
6.5085 |
0.05652 |
0.03578 |
0.00517 |
0.00080 |
0.00015 |
|
|
1.0 |
0.053 |
6.3390 |
0.05652 |
0.05287 |
0.00764 |
0.00118 |
0.00022 |
|
|
1.5 |
0.067 |
6.1017 |
0.03498 |
0.05652 |
0.01319 |
0.00204 |
0.00038 |
|
|
2.0 |
0.079 |
5.8983 |
0.02190 |
0.05652 |
0.02108 |
0.00326 |
0.00061 |
|
|
2.5 |
0.089 |
5.7288 |
0.01482 |
0.05652 |
0.03114 |
0.00482 |
0.00090 |
|
|
3.0 |
0.099 |
5.5593 |
0.01003 |
0.05652 |
0.04601 |
0.00713 |
0.00132 |
|
|
3.5 |
0.109 |
5.3898 |
0.00679 |
0.04699 |
0.05652 |
0.01053 |
0.00196 |
|
|
4.0 |
0.121 |
5.1864 |
0.00425 |
0.02942 |
0.05652 |
0.01681 |
0.00313 |
|
|
4.5 |
0.132 |
5.0000 |
0.00276 |
0.01915 |
0.05652 |
0.02583 |
0.00481 |
|
|
5.0 |
0.143 |
4.8135 |
0.00180 |
0.01246 |
0.05652 |
0.03968 |
0.00740 |
|
|
5.5 |
0.153 |
4.6440 |
0.00122 |
0.00844 |
0.05448 |
0.05652 |
0.01091 |
|
|
6.0 |
0.163 |
4.4745 |
0.00082 |
0.00571 |
0.03688 |
0.05652 |
0.01613 |
|
|
6.5 |
0.172 |
4.3220 |
0.00058 |
0.00402 |
0.02595 |
0.05652 |
0.02291 |
|
|
7.0 |
0.182 |
4.1525 |
0.00039 |
0.00272 |
0.01757 |
0.05652 |
0.03385 |
|
|
7.5 |
0.192 |
3.9830 |
0.00026 |
0.00184 |
0.01189 |
0.05652 |
0.05002 |
|
|
8.0 |
0.202 |
3.8135 |
0.00018 |
0.00124 |
0.00805 |
0.04322 |
0.07390 |
|
|
8.5 |
0.213 |
3.6271 |
0.00012 |
0.00081 |
0.00524 |
0.02814 0.11352 Продолжение таблицы 2 |
||
|
V , мл |
f 1 |
f 2 |
f 3 |
f 4 |
рК 1 |
рК 2 |
рК 3 |
pK 4 |
|
0.3 |
0.5801 |
0.3342 |
0.1925 |
0.1109 |
6.073 - |
|||
|
0.5 |
0.5644 |
0.3162 |
0.1771 |
0.0992 |
6.061 - |
|||
|
0.8 |
0.5327 |
0.2811 |
0.1483 |
0.0782 |
6.036 - |
|||
|
1.0 |
0.5114 |
0.2586 |
0.1308 |
0.0661 |
6.019 - |
|||
|
1.2 |
0.4965 |
0.2434 |
0.1193 |
0.0585 |
6.006 - |
|||
|
1.5 |
0.4682 |
0.2158 |
0.0995 |
0.0458 |
5.980 - |
|||
|
2.0 |
0.4280 |
0.1794 |
0.0752 |
0.0315 |
- 5.092 |
|||
|
2.5 |
0.3905 |
0.1484 |
0.0563 |
0.0214 |
- 5.049 |
|||
|
3.0 |
0.3513 |
0.1189 |
0.0402 |
0.0136 |
- 4.999 |
|||
|
3.5 |
0.3271 |
0.1022 |
0.0319 |
0.0100 |
- 4.964 |
|||
|
4.0 |
0.3116 |
0.0921 |
0.0272 |
0.0080 |
- 4.941 |
|||
|
4.5 |
0.2905 |
0.0792 |
0.0216 |
0.0059 |
4.095 |
|||
|
5.0 |
0.2652 |
0.0648 |
0.0158 |
0.0038 |
4.048 |
|||
|
5.5 |
0.2434 |
0.0534 |
0.0117 |
0.0025 |
4.001 |
|||
|
6.0 |
0.2425 |
0.0529 |
0.0115 |
0.0025 |
3.999 |
|||
|
6.5 |
0.2370 |
0.0501 |
0.0106 |
0.0022 |
3.985 |
|||
|
7.0 |
0.2265 |
0.0451 |
0.0090 |
0.0018 |
3.229 |
|||
|
7.5 |
0.2131 |
0.0388 |
0.0071 |
0.0013 |
3.191 |
|||
|
8.0 |
0.2028 |
0.0342 |
0.0057 |
0.0010 |
3.273 |
|||
|
8.5 |
0.1893 |
0.0282 |
0.0042 |
0.0006 |
3.405 |
|||
В таблице 2 сведены все исходные данные для расчета констант диссоциации по уравнениям (1) и (2) при титровании 0.01413М (0.05652н.) раствора 3,3’4,4’- тетрааминодифенилоксида, широко применяемого в синтезе полибензимидазолов, 0.1295 н. раствором хлорной кислоты в среде ДМФ.
Как видно из таблицы 2 и рисунка 1, равновесные концентрации частиц, находящихся в титруемом растворе, вполне сопоставимы. Поэтому подчеркнем, что в расчетах рК а все концентрации должны быть учтены.
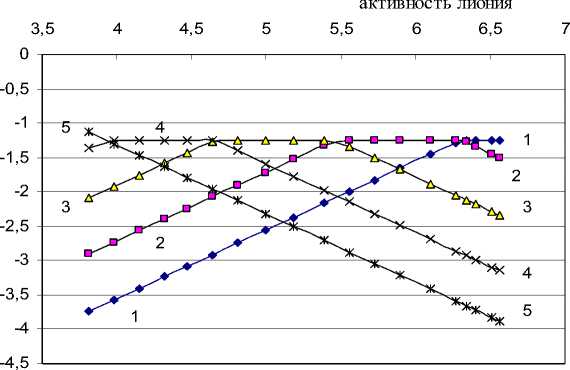
Рис.1. Логарифмическая диаграмма процесса титрования 0,05652н. раствора 3,3’4,4’-тетрааминодифенилоксида 0.1295 н. раствором хлорной кислоты в среде ДМФ, дающая возможность определения концентраций равновесных частиц: 1-1: lg [B], 2-2: lg[BH+], 3-3: lg[BH 2 2+], 4-4: lg[BH 3 3+], 5-5: lg[BH 4 4+]
Протонированные четырехкислотные основания характеризуются близостью констант кислотности, подтверждаемой одним совместным скачком потенциала на кривой потенциометрического титрования, которую мы здесь не приводим.
Рассчитанные в соответствующих буферных областях величины термодинамических констант диссоциации протонированного 3,3’4,4’-тетрааминодифенилоксида в среде ДМФ равны: рК 1 = 6.03 ± 0.05, рК 2 = 5.01 ± 0.08, рК 3 = 4.03 ± 0.06, рК 4 = 3.27 ± 0.12.
Разработанная методика определения термодинамических констант кислотности полиоснований в среде органических растворителей вполне приемлема при экспериментальном определении рК а любых четырехкислотных оснований при многостадийном протонировании (равно как и трехкислотных оснований [12]).


