Теоретическая попытка определения угловой скорости сферического диска

В наших исследованиях сферический диск работал как окучник в почве, подготовленной к посеву, находящейся в рыхлом состоянии, заглублялся на глубину 5-7 см. Тяговое сопротивление не имеет основного значения вследствие недогруженности пропашного трактора типа ТТЗ-80.10 при посеве. Важно знать траекторию полета частиц, отбрасываемых диском, дальность их отбрасывания. При теоретическом определении траектории движения частиц по сферической поверхности, значительную роль при определении момента срыва скорости частицы играет угловая скорость сферической поверхности диска. Для определения влияния, причин, влияющих на угловую скорость, мы провели исследования. Сферический диск, заглубленный в рыхлую почву, вступает во взаимодействие с ней и движется с определенной угловой скоростью вращения W. Частицы почвы поступают во внутреннюю полость сфары, затем сходят с диска и опадают на определенном расстоянии. На угловую скорость W влияют:

• 1 .Соотношение моментов инерции диска и почвы

• 2 .Трение в подшипнике

• 3 . Сопротивление врезанию передний грани сферы и освобождению задней грани от почвы

• 4 .Угол атаки.

Момент инерции диска относительно оси вращения Z (рис.1) есть

J Z

МR

Где M- масса диска; R-радиус диска.

Для определения угловой скорости W применим теорему об изменении относительно оси вращения Z кинетического момента системы, состоящей из почвы и диска. Для этого изображаем систему “диск-почва” и внешние силы, действующие на систему (рис. 1).

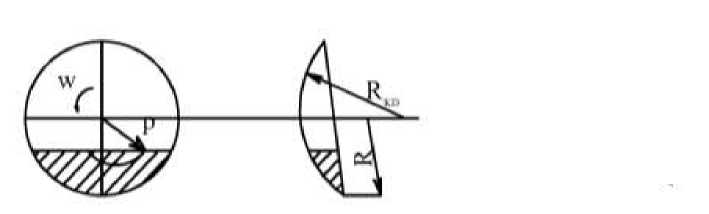
Рис 1. Сферический диск, заглубленный в почву.

Но нами не учтен момент трения в подшипнике, сопротивление врезанию передней части диска и выглубление задней. Очевидно, в действительности эти факторы увеличивают радиус перекатывания на величину AR , колеблющуюся в небольших пределах , которая зависит от конструктивного оформления подшипника, кривизны сферы, коэффициента трения почвы о диск

R = R + ΔR pp

.

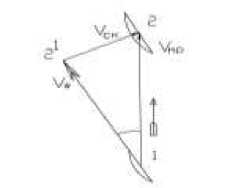
Теперь определим изменение угловой скорости ω в зависимости от угла установки диска – угла атаки (рис 2) .

Сферический диск, движущийся совместно с трактором и имеющий поступательную скорость трактора при перемещении по прямой линии совершает сложное движение. Он одновременно участвует в движении чистого качения и чистого скольжения при перемещении по прямой из положения 1 в положение II. Скорость такого движения можно выразить равенством

Где   ϑ _ck - скорость трактора: ϑ_ω -скорость чистого скольжения :

• ϑ mp – скорость чистого качения:

Из треугольника I II II` имеем:

ϑω = ϑmp ⋅ cosα

Для определения действительного радиуса перекатывания R пер а также угловой скорости сферического диска, нами была изготовлены сферические диски с различными радиусами кривизны R крив при различной толщине t ( ф =300 мм).

R крив ,   500  700  900 Плоский мм

• t    , мм 3     3     3   3  5  8   12

Радиус перекатывания сферического диска вычислен следующим образом. На опциальном устройстве , который был изготовлен в САИМЭ , определено число оборотов сферического диска , а также части оборота до I0 , отсчитано время движения по секундомеру до 0.01 . Устройство было укреплено на ходовой тележке почвенного канала, что позволяло крепить сферический диск на нужный угол атаки к траектории движения в пределах от 20 до 700 с шагом 100 .

Тележка канале двигалась с четырьмя различными скоростями .

При проведении эксперимента подсчитывалось число оборотов диска N и время движения t , причем число оборотов N складывалось из числа целого число оборотов n и чести оборотов Δ n

N = n + Δn

т.е.

Oпыты велись на расчетном участке Z, радиус перекатывания определен как

R

1 пер

z

2 π N

эксперименты проводились в 4- кратной повторности в каждом варианте .

Сферические диски с различными моментами инерции и радиусами кривизны заглублялись на глубину 30 : 60 : 90 : 120 мм и двигались с различными скоростями .

После обработки экспериментальных данных выяснилось , что на угловую скорость кривизна сферической поверхности , момент инерции, а также заглубление диска в почву практически не влияет. Приблизительно такие же данные получены и при других углах атаки.

Основным фактором, влияющим на радиус перекатывания и соответственно на угловую скорость оказался угол атаки α .

Вычисление радиуса перекатывания по приведенной нами выше формуле показало, что радиус перекатывания Rnep во всех случаях приближается к величине R (рис. 1) .

Эксперименты показали, что формула (15) может быть упрощена до вида:

ϑ ⋅ cos α

W = ^mp

R

На рис. 3 даны зависимости угловой скорости W от угла установки а. Здесь показано значение угловой скорости сферического диска, вычисленное по формуле (16) и экспериментальным данным. Угловая скорости зависит лишь от угла установки диска к траектории, скорости движения и может быть подсчитана по формуле (16) .

Выводы

Угловая скорость сферического диска, двигающегося в почве, подготовленной к посеву, не зависит от кривизны диска, величины заглубления, а также момента инерции диска.