Теоретические аспекты построения термодинамических моделей электродвигателей

В настоящее время в экономике России используются десятки миллионов электродвигателей. В большинстве промышленных установок с электроприводом мощность двигателей завышена на 20–40 %, что говорит о существовании возможностей для снижения стоимости электропривода и потребления электроэнергии им за счет более рационального выбора мощности двигателей [1]. С учетом того факта, что классические косвенные методы оценки теплового состояния двигателей не всегда дают адекватный результат [2], возрастает роль численных методов расчета на основе термодинамических моделей (ТДМ). Значение математического моделирования для оценки теплового состояния двигателей повышается также из-за того, что функционирование механической части электропривода может иметь свои особенности, которые часто затруднительно учесть аналитически [3, 4].

Существует два подхода к численному моделированию тепловых процессов в электрических машинах - моделирование на основе тепловых схем (ТС) с сосредоточенными параметрами и на основе использования пространственно-временной дискретизации объекта исследования (FEM- и CFD-моделирование). При всех преимуществах FEM и CFD, в задачах термодинамического моделирования электрических машин, эти подходы часто требуют построения трехмерных моделей [5, 6], что обусловливает очень высокие требования к вычислительным ресурсам и длительное время решения таких задач. Термодинамические модели на основе ТС с сосредоточенными параметрами предъявляют значительно меньшие требования к вычислительным ресурсам, обеспечивают сравнительно быстрый расчет, что позволяет использовать их при решении задач, связанных с перебором значительного количества вариантов, например при анализе чувствительности модели к изменениям параметров [5, 7, 8]. Также ТДМ на основе ТС позволяют, в некоторых случаях, провести исследования аналитическим путем с целью выяснения влияния особенностей модели на температуру элементов машины в установившихся и переходных режимах. Это обусловливает актуальность создания и исследования таких ТДМ электрических машин.

В настоящей работе ставится задача получения математического описания обобщенной термодинамической модели электродвигателя на основе метода тепловых схем и исследования некоторых свойств и особенностей функционирования этой модели.

1. Математическое описание термодинамической модели

В литературе приводятся различные формы математического описания моделей электрических машин, пригодные для исследования термодинамических процессов и/или установившегося теплового режима. Так, в [9] рассматривается термодинамическое уравнение для одной греющейся массы, в [10, 11] рассматриваются ТС с несколькими узлами с точки зрения исследования установившегося теплового режима. В [12, 13] получено математическое описание термодинамических процессов для системы, состоящей из двух и трех греющихся масс, а в [14] предложена система уравнений для расчета тепловых переходных процессов, состоящая из восьми уравнений для статора и семи – для ротора электрической машины. В [15-18] дано математическое описание термодинамических процессов в виде дифференциального уравнения в матричной форме для произвольного количества греющихся масс. Однако во всех упомянутых случаях математическое описание получено для одной температуры охлаждающей среды. В то же время существуют электрические двигатели с использованием жидкостного охлаждения, например асинхронные короткозамкнутые взрывозащищенные двигатели серии ЭКВ [19], в которых применяется способ охлаждения двигателя ICW37 - водяное охлаждение корпуса. Выпускаются с водяным охлаждением также тяговые электродвигатели. Некоторые крупные двигатели выпускаются с двумя контурами охлаждения – водяным и воздушным. Например, высоковольтные двигатели АЗ-3000-10-1000УХЛ4, АСЗ-3150-10-375УХЛ4, АН32-18-66-12Т3 со степенью защиты IP44 имеют воздушно-водяное охлаждение ICW37A97 и ICW37A91, двигатели серии АЗМ и АЗМС (IP44) используют способ охлаждения ICW37А71 [20]. В подобных случаях возникает вопрос о необходимости учета в математическом описании не единственной температуры охлаждающей среды.

Также в некоторых случаях приходим к ТС с несколькими температурами охлаждающей среды и при необходимости учета постепенного повышения температуры охлаждающего потока внутри машины, как при аксиальной, так и при радиальной системе вентиляции [21, 22], что актуально для крупных машин как защищенного, так и закрытого исполнения. В [22] получены уравнения теплового баланса электродвигателя для произвольного количества температур охлаждающей среды, но эти уравнения приведены в форме, пригодной лишь для исследования установившегося режима.

Получим обобщенное математическое описание термодинамических процессов в электрическом двигателе для произвольного количества греющихся элементов (узлов ТДМ) при произвольном количестве охлаждающих сред. Обозначим количество узлов модели – n , а количество охлаждающих сред – m .

Рассмотрим тепловой баланс для i -го узла. Количество тепла, выделяющееся за элементарный промежуток времени dt в i -м узле, определяется суммарной мощностью потерь (AP _t ) в нем:

Qu = ДР.                               (1)

Количество тепла, отданное i -м узлом другим узлам, определяется разностью их температур:

Q21 = E% i (9 / - *А            (2)

(j*t)

где j – номер узла, с которым происходит тепло- обмен, j∈{1,n}, j≠i; θi и θj – температуры узлов, между которыми происходит теплообмен; λij – тепловая проводимость между узлами i и j.

Количество тепла, отданное i -м узлом в охлаждающие среды:

Q u = Е ^=1 (9 / - 9 _0k )X ₀/_k dt,                (3)

где k – номер охлаждающей среды; θ_{o k} – температура k -й охлаждающей среды; X _otk - тепловая проводимость между i -м узлом и k -й охлаждающей средой.

Количество тепла, затраченное на изменение температуры i -го узла, определяется его теплоемкостью C_i :

Q 4t = W .                        (4)

Уравнение теплового баланса

Qit = Q2t + Q3t + Q4t, с учетом (1)–(4), получим дифференциальное уравнение, описывающее изменение температуры i-го узла:

^APt = ^Ct "57 + ^Vn = i ^{( 9} t ^- ^У^Ч +

(i*t)

+ EW9 _t - Q okKtk .                  (5)

После преобразований из (5) можно записать:

C t^ = AP t - 9 t j V '    X_t j + X ^₌i ^ otk ) +

E% i 9 j X_tj +X k?=i 9 ^JSotk .                (6)

(j*t)

Учтем влияние температуры узлов термодинамической модели на мощность греющих потерь в них. Для потерь в обмотках машины используем известную линейную зависимость сопротивления от температуры. Температурная зависимость других видов потерь может быть приведена к линейному виду путем линеаризации в пределах актуального диапазона изменения температуры этих узлов. При объединении нескольких элементов конструкции электрической машины в один узел ТДМ в нем может оказаться более одного источника греющих потерь, каждый из которых имеет свою зависимость мощности потерь от температуры. Поэтому представим суммарную мощность потерь в i -м узле следующим образом:

^APt = E /=i ^APst.t(i) [1 + k ₆t(i)⁽ 9 t ^- 9 _st.t(i) )], ⁽⁷⁾ где s - количество источников потерь в i -м узле; AP s_t._t(i) — мощность потерь в l -м источнике i -го узла; k _9t(t) - температурный коэффициент для l -го источника потерь в i -м узле; 9 _{st t}(_l) - температура для l -го источника потерь в i -м узле, относительно которой рассчитывается мощность этого источника.

Для тех узлов, где нет зависимости мощности потерь от температуры, принимаем k _{9 t}y ) = 0.

Запишем (6) с учетом (7):

C t^ = AP t - 9 t (Eⁿ j=i Xij + E ^.i X otk -

\ (j*t)

^—VSl=1^APst.t(l) ^k9t(/)^{) + Vn}j.i ⁹ jklj ,           ⁽⁸⁾

(j*t)

где ^Apt = ^Ap_st.t(i)^{[1 - k}9t(/) ⁹ st.t(/) ] ⁺ E fcLi ⁹ ok ^k otk .

Как видим из (8), введение учета зависимости мощностей потерь в узлах модели от температуры при линейной связи этих величин не нарушает линейность дифференциального уравнения для i-го узла (здесь и далее принимаем допущение об отсутствии температурной зависимости теплоемкостей и тепловых проводимостей). Это дает возможность записать (8) в векторно-матричной форме, для чего введем следующие обозначения: ДР' -матрица-столбец мощностей потерь в узлах модели размерностью nxl; 0 - матрица-столбец температур узлов размерностью nxl; C - диагональная матрица теплоемкостей узлов размерностью nxn; Л - симметричная (Xij = X ji) общая матрица теп ловых проводимостей размерностью nxn.

■ДР 1"

Др2

ДР ' =

′

; е#Ч1 o_RJ

[ДР^

Л =

| Хц ^Х 12 '" ^Х 1П "I ^Х 21 ^{— Х} 22 ^ ^Х 2п

^Х П1 ^Х П2      ^Х ПП-1

' П1

Диагональные элементы в матрице проводи-

мостей Л определяются следующим выражением:

^ = :SU Хо^ + 2% 1 Ху—

(j*D

• ^— £ г=1^ДР;^(0 ^p0i(i) .                           ⁽⁹⁾

• 2.    Исследование решения уравнения термодинамической модели

С учетом введенных обозначений уравнение (8) в векторно-матричной форме запишем следующим образом:

с—= др' + ле.                      (10)

dt

Уравнению (10) соответствует векторно-матричная структурная схема, показанная на рис. 1.

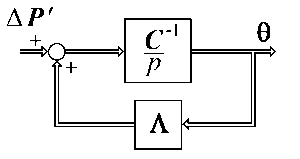
Рис. 1. Структурная схема термодинамической модели двигателя при произвольном количестве базовых температур

Исследуем свойства решения уравнения (10) в случае, когда привод работает при неизменных параметрах внешней среды, при постоянстве нагрузки и скорости. При этих условиях мощность потерь в узлах модели будет зависеть только от температуры этих узлов. Для выяснения характера процессов в рассматриваемой ТДМ представим уравнение (10) в следующем виде:

— = ле + р , dt

где Л = С-1Л; Р=С"1 ДР'.

Запишем общее решение уравнения (11) [23, 24]:

^е = ^{6 e}initiai + /о6((-5№Ш (12) где e _initial - вектор начальных температур узлов модели; G(t — s) = e^л(t_s)- матрица Грина размерностью n x n .

Взяв интеграл в уравнении (12), получим:

^е = ⁽ Р ^— ^^{t )e}steady ^{+ e Лt е}initiaZ , ⁽¹³⁾ где e _st_eady = —Л " ¹Р = —Л " ¹ДР ' - вектор установившихся значений температур, Р - единичная диагональная матрица размерностью n x n .

Характер изменения во времени температуры узлов будет определяться характером изменения свободных составляющих решения уравнения (11), так как вектор внешних воздействий на систему в рассматриваемом случае постоянен (изменение мощности потерь из-за изменения температуры учтено в диагональных элементах матрицы A ). Это означает, что вид процессов будет определяться характером и знаком собственных чисел матрицы A [23]. Из практики известно, что свободные составляющие термодинамических переходных процессов в электрических машинах носят апериодический затухающий характер. Выясним, всегда ли справедливо это утверждение. Свободные составляющие переходных процессов могут иметь указанный характер только в том случае, когда все собственные числа матрицы системы являются вещественными и отрицательными.

Сформулируем теорему:

Матрица A = C ^–1 Λ , где C и Λ – симметричные матрицы порядка n , имеет вещественные собственные числа Х (_Л) .

Симметричные матрицы имеют вещественные собственные числа, однако матрица A , являясь произведением двух симметричных матриц C ^–1 и Λ , не обязательно сама должна быть симметричной, поэтому неочевидно, что ее собственные числа вещественные. Докажем эту теорему, опираясь на подход, предложенный Ф.Р. Гантмахером [24]. Введем вспомогательную матрицу

У = VC (14) в смысле V · V = С и V · V ^–1 = E , где E – единичная диагональная матрица.

Правомерность использования (14) в данном случае следует из того, что для положительно определенной матрицы C существует положительно определенная матрица VC, такая, что (VC)2 = С [25]. Из физического смысла ясно, что матрица C положительно определена, так как ее диагональные элементы определяются теплоемкостями. Также отметим, что если Х(С) - собственные числа матрицы C, то собственными числами матрицы VC будут числа JX(C) [25]. Поскольку матрица C диагональная, ее собственные числа равны ее диагональным элементам, которые ненулевые. Это зна- чит, что матрица C невырожденная, но тогда и VC будет невырожденная, так как все Jx(C)^0. Поэтому для матрицы V существует и обратная матрица V–1. С учетом (14) и перечисленных выше обстоятельств, A = C–1Λ можем записать в виде л = (Vc)"1(Vc)"1A(Vc)"1Vc,(15)

то есть

Л = У_15У,(16)

где

5 = У“1ЛУ“1.(17)

Для диагональной матрицы V (поскольку C диагональная) и симметричной матрицы Λ , матрица S также является симметричной матрицей. Поскольку S вещественная и симметричная, то она имеет вещественные собственные числа [23]. Выражение (16) показывает, что матрицы A и S связаны преобразованием подобия. Матрицы, обладающие свойством подобия, имеют один и тот же спектр собственных чисел [25], откуда следует вещественность собственных чисел матрицы A . Теорема доказана.

Исследуем вопрос о знаке собственных чисел матрицы A . Рассмотрим сначала процессы в ТДМ без учета зависимости мощности потерь в узлах от температуры. При k _6t = 0 модуль каждого диагонального элемента матрицы тепловых проводимостей Λ в соответствии с (9) равен:

Rd = £ £=1 ^X otk + Е" =1 Л . , (i = 1.....n), (18)

(j*t)

Из (18) следует, что для матрицы Λ выполняется условие диагонального преобладания по строкам. Учитывая, что все элементы в каждой строке матрицы A получены делением элементов соответствующей строки матрицы Λ на одно и то же значение теплоемкости ( a_i j = λ _i j / C_i ), для элементов матрицы A также выполняется условие диагонального преобладания по строкам:

|a_tt| = E^ ik + E% 1 a_v,(i = 1.....n). (19)

U*t)

В соответствии с теоремой Гершгорина [24], каждое собственное число матрицы А всегда расположено в области локализации (в круге Гершго-рина), определяемой соотношением:

ktt - x| < E” =1 a .. , (i = 1,   ,n).        (20)

(j*t)

Перепишем соотношение (20) с учетом знака диагональных элементов a _tt следующим образом:

|x + E £=1 a otk +E” =1 « tj l 1 a_u.   (21)

I                           (j*t)     |       (j^t)

Поскольку £ ™=₁ a _otk > 0 и £’ j=i a _t. > 0, ясно, (j*t)

что условие (21) может выполняться только при отрицательных значениях Х (_Л)_к . Причем должно быть

Х . <    £/' г л ... .                         (22)

Таким образом, доказано, что при отсутствии зависимости мощности потерь в узлах ТДМ от температуры этих узлов, изменение во време- ни свободных составляющих термодинамических процессов в этой модели всегда имеет апериодический затухающий характер.

Отметим, что сформулированное выше положение относится не только к термодинамическим процессам в электрических машинах, но имеет и более общий характер. Оно справедливо для любых термодинамических систем с симметричными матрицами тепловых проводимостей. Иногда в тепловых схемах электрических машин используют однонаправленные тепловые проводимости, например, в тепловых схемах двигателей защищенного исполнения [22]. Однако такие тепловые проводимости определяют перетоки тепла по направлению к охлаждающим средам и поэтому входят только в диагональные элементы матрицы Λ , не изменяя ее симметричного характера.

• 3.    Влияние температурного изменения сопротивлений обмоток на свойства модели

Теперь рассмотрим свойства системы с учетом зависимости мощности потерь в узлах от температуры. В этом случае модуль каждого диагонального элемента матрицы Λ в соответствии с (9) определяется следующим образом:

• |x _tt | = 1е^₌₁ л ... . v.   x_v-

• I               о*о

• -£ =1 АР_Л.одк_вад|.                      (23)

С учетом (23) запишем выражение для матрицы A , определяющее область локализации ее собственных чисел:

lx .Е^а^Е^ х a .. -

I                           (j*t)

• Г . V AP .. k ...     < V .     a .. .       (24)

(j*t)

Анализ неравенства (24) показывает, что при E f=1 ^P st. _t(i) k e_t(() ^0 оно может выполняться как при отрицательных, так и при положительных значениях Х (_Л) (включая и Х (_Л) = 0). В любом случае для этого должно выполняться неравенство

• ^Х (_Л) < ^ t ^{1 (} E^s =1 ^ ^Pst.t(z) ^ket(i) —£ £=1 ^x ot _ky ⁽²⁵⁾

Из (25) видно, что при ^£=1 AP st.t(i) к ₆._ю >

• > V k=₁ Л _о1к может оказаться, что Х (_Л)) > 0. Это соответствует ситуации неограниченного увеличения температуры i -го узла без выхода на установившийся уровень.

В таблице приведены значения собственных чисел матрицы A = C ^–1 Λ для 6-массовой ТДМ двигателя 4A100L4 (модель включает в качестве своих узлов обмотку статора с разделением на лобовые и пазовую части, сталь статора, внутренний воздух, ротор и корпус).Обозначено: M / M N - относительная величина момента двигателя. Учитывалось влияние изменения температуры на мощность потерь в обмотках статора и ротора.

На рис. 2 и 3 показаны графики изменения превышения температуры (τ) лобовых частей об-

Величины собственных чисел матрицы А

Двигатель 4A100L4
M / MN	0	0,5	1,0	1,5	2,0
	–361,7809	–361,7808	–361,7807	–361,7805	–361,7802
	–10,2185	–10,1960	–10,1285	–10,0160	–9,8586
Х№ •100, 1/c	–2,5035	–2,4870	–2,4383	–2,3600	–2,2567
	–1,0839	–1,0786	–1,0621	–1,0327	–0,9878
	–0,0594	–0,0554	–0,0427	–0,0196	+0,0165
	–0,2781	–0,2729	–0,2578	–0,2334	–0,2005

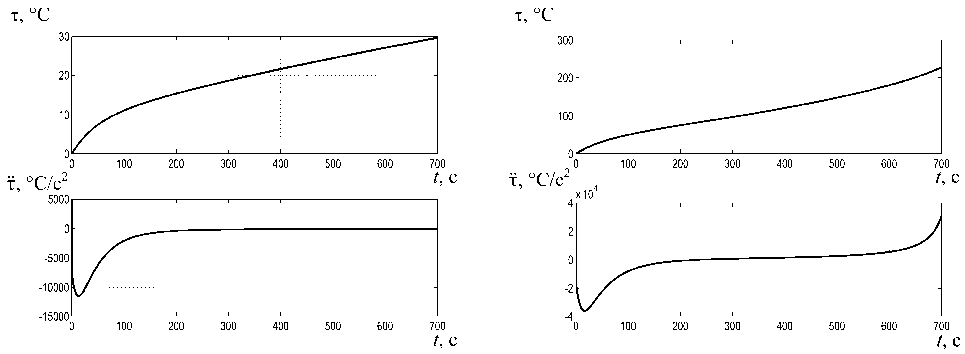
Рис. 2. Графики т( t ) и t ( t ) при M/ M n = 1,0

Рис. 3. Графики т( t ) и t ( t ) при M/ M n = 2,0

мотки статора двигателя 4A100L4 и второй производной этой величины (т) при разных величинах нагрузки. Рис. 2 соответствует ситуации, когда все собственные числа матрицы А отрицательны, а рис. 3 - ситуации, при которой одно из собственных чисел имеет положительное значение (см. таблицу) и процесс нагрева двигателя приобретает характер «теплового саморазгона», о чем свидетельствует переход графика второй производной в положительную область.

Выводы

• 1.    Получено обобщенное математическое описание ТДМ электрической машины для произвольного количества узлов и охлаждающих сред, учитывающее влияние температуры узлов на величину греющих потерь, выделяющихся в этих узлах.

• 2.    Показано, что введение учета зависимости мощности потерь в узлах ТДМ от температуры этих узлов при линейной (или линеаризованной) связи этих величин не изменяет свойство линейности модели.

• 3.    Аналитически доказано, что при отсутствии зависимости мощности потерь в узлах ТДМ от температуры этих узлов изменение во времени свободных составляющих термодинамических процессов в этой модели всегда имеет апериодический затухающий характер, однако при наличии температурной зависимости мощности потерь это положение не всегда справедливо. Аналитически определены условия, при которых в случае нали-

• чия температурной зависимости мощности потерь происходит неограниченное увеличение температуры элементов электрической машины без выхода на установившийся уровень.