Теоретические аспекты прогнозирования работы предприятий сервиса в условиях кризиса

Перед каждым предприятием, предоставляющим разнообразные сервисные услуги, и в особенности в большом количестве, встает вопрос – как на них отразится экономический кризис. Ниже представлен теоретический материала, который раскрывает механизм влияния разнообразных сил на все виды бизнеса и его реакция на них. В своих работах ряд авторов описали кризисные процессы, протекающие в экономике [1, 5]. Их основным недостатком является то, что в них не представлен необходимый математический аппарат, позволяющий описывать процессы, происходящие в экономике, с помощью которых можно прогнозировать в будущие кризисы. В работе [2, 6] автор показал, что экономику любой страны можно представить в виде трех оболочек: малого, среднего и большого бизнеса. При воздействии внешних или внутренних сил (либо при их совместном воздействии) экономические оболочки деформируются и их деформацию можно свести к таким видам как: расширение и сжатие [3]. При этом под одновременным расширением (сжатием) экономических оболочек (либо при их совместном расширении и сжатии) подразумевается то, что это может происходить как пропорционально, т.е. по одному какому-то математическому закону и на одну и туже величину, так и не пропорцио- нально, т.е. по разным математическим законам.

Так как силы РV, воздействующие на экономическую оболочку, могут различаться по своей относительной величине, то введем для них следующих три градации: Рb   большая внешняя (внутренняя) сила;

Рm  средняя внешняя (внутренняя) сила; Рs малая внешняя (внутренняя) сила.

Примем значение силы Р V со знаком “ ” для внешних сил, которые сжимают экономическую оболочку, отчего она деформируется и ее объем уменьшается. Если же на экономическую оболочку воздействуют внутренние силы, то будем их считать положительными, т.е. со знаком “+”, т.к. в этом случае экономическая оболочка также деформируется, но при этом её объем увеличивается.

На рис. 1 представлен вид распределения силы деформации РV экономической оболочки, исходя из которого можно вы- вести следующие выражения:

Р b = + A Р b max + I- Р b max I, Р m = + A Р m max + I-A Р m max I , Р s = + A Р s max + I-A Р s max .

Здесь: AРi   величина силы дефор- мации РV экономической оболочки.

Таким образом, величину силы деформации  РV экономической оболочки можно представить следующим уравнением:

Р = А Р₆ + А Р_т + А Р , = + P bm _тах + | -A P m max | +

(+A P m max )  +

I- А Р , maxi = 100%.

m max I ^{+  (+} ^P_s max )   ⁺

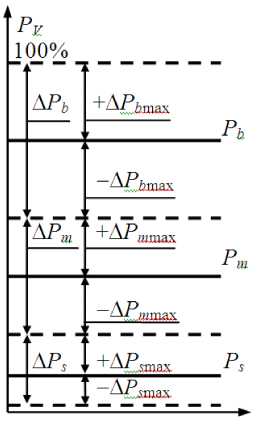
Рис. 1 - Распределение сил деформации P V экономических оболочек

Рассмотрим два основных вида деформации оболочек.

Первый, когда все три экономической оболочки расширяются.

Это может происходить только тогда, когда все силы действуют изнутри (рис. 2).

При этом могут быть три следующих варианта:

все экономические оболочки расширяются пропорционально предыдущим своим состояниям по всем осям (рис. 2 а );

все экономические оболочки расширяются не пропорционально предыдущим своим состояниям по всем осям;

• все экономические оболочки расширяются в одних или нескольких отдельных областях (рис. 2 b , c , d , e ).

На рис. 2 m изображены для наглядности две экономические оболочки, хотя на самом деле V_m g = V fn .

Рассмотрим эти расширения по отдельности:

Пропорциональное    расширение всех экономических оболочек означает, что на них воздействуют равномерно по всей поверхности одинаковые внутренние силы. При этом все экономические оболоч- ки расширяются пропорционально на какой-то определенный процент. Здесь следует учесть, что силы, действующие на экономические оболочки в этом случае, отличаются, по своей величине, т.к. трудно себе представить, чтобы сила, действующая на экономическую оболочку малого бизнеса, произведет аналогичное изменение других экономических оболочек в процентном соотношении. Возможные варианты расширения оболочки представлены на рис. 3.

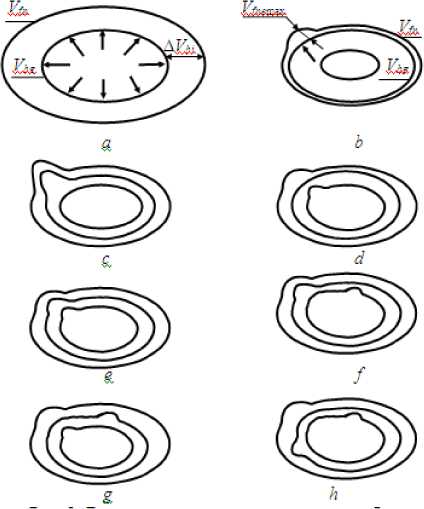
Рис. 2- Виды расширения экономических оболочек: а - пропорциональное расширение экономической оболочки; b - расширение экономической оболочки в отдельной области; Vmg - начальное состояние экономической оболочки, Vf - конечное состояние экономической оболочки, Vmnemax -максимальное расширение экономической оболочки в отдельной области; c, d, e, f, g, h -варианты расширения экономических оболочек.

Для описания состояний оболочек введем величину относительного увеличения (уменьшения) A V_eo , которая будет описана ниже, т.к. она позволяет более полно охарактеризовать измененное состояние экономической оболочки и производить сравнение при их расширении или сжатии (5)

V eo = ( V fn – V bg ) / V fn  [или    V eo = ( V fn –

V bg )100% / V fn ].                         (5)

где:  Veо – величина относительного измене ния объема экономической оболочки; Vbg – начальное состояние объема экономической оболочки до воздействия на нее внешних (внутренних) сил; Vfn – конечное состояние объема экономической оболочки после воздействия на нее внешних (внутренних) сил.

Теперь введем значение разницы объема экономической оболочки V e , между конечным V fn и начальным V bg состоянием, которую можно записать в виде следующей формулы (6) (рис. 3 b )

V e = V fn – V bg .                           (6)

В зависимости от значений Vbg и Vfn величина  Ve может быть как положитель ной, при Vfn > Vbg, когда экономическая оболочка расширяется (рис. 3), так и отрицательной при Vbg > Vfn когда экономическая оболочка сжимается, либо равна нулю Ve = 0. Расширение экономической оболочки соответствует активизации рынка, а сжатие означает кризисную ситуацию.

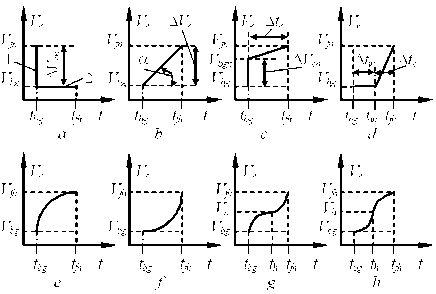
Рис. 3 - Варианты расширения экономической оболочки

Обозначим время, за которое происходит расширение (сжатие) экономической оболочки как t e (рис. 3 d ) и оно рассчитывается по формуле (7)

t_e = t f _n t b _g = ( t_in t b _g ) + ( t f _n t_in ). (7)

Для того чтобы все три экономические оболочки расширялись (сжимались) пропорционально на одинаковый процент введем величину коэффициента расширения (сжатия) K ec , который характеризует, на сколько надо увеличить (или уменьшить)

силу, воздействующую на малый, средний или большой бизнес Рsb, чтобы в других оболочках произошли аналогичные про- порциональные изменения, т.е. можно записать, например, Рmb = Keci Рsb или Рbb = Kecj Рsb. Здесь обозначения i и j коэффициентов Kec введены для того, чтобы отличать их для среднего и большого бизнеса соот- ветственно.

Если же применить выведенный выше коэффициент K exs , то можно записать универсальное выражение (8)

р + р + р =

^P sb 1     P sb 1    ’”•’ P sbn

n

ЕР = К Р ^ К Р + К Р = Psbi    Kec 1 Psb 1 Kec 2 Psb 2   ’”•’ Keen Psbn i1

n

^K ecn^-⁴ P sbi — ^K ec 1 ^P bb 1 ^{+ K} ec 2 ^P bb 2 ⁺,’”’ ^K ecn ^P bbn " i 1 n

K ecn^ P bbi                                    ( ⁸ )

i 1

Для значений коэффициента расширения (сжатия) экономической оболочки можно записать следующие границы 0 >  K ec >> 1.

Так как экономические оболочки не могут за короткий промежуток времени значительно расшириться, то введем понятие коэффициента максимального одноразового расширения Kecemax и время, за которое это расширение может произойти tecemax. Здесь следует сразу оговорится, что tecemax 0. Таким образом, можно записать величину одноразового конечного состояния объема экономической оболочки после воздействия на нее внешних (внутренних) сил (9) Vfn = Kecemax Vbg f(tecemax).

Непропорциональное расширение экономических оболочек. При воздейст- вии одинаковых внутренних сил на все три экономические оболочки одновременно их реакция будет разной, следовательно, и объем этих оболочек будет изменяться по-разному. В этом случае должны соблюдаться следующие равенства, когда экономическая оболочка среднего бизнеса увеличивается на величину Mb ( Mbmax)

S b +   S b max   M b + M b ;    S b + S b max   M b +

M b max ;

S b +   S b   M b + M b max .               (10)

Экономические оболочки расширяются в одной или нескольких отдельных областях. На рис. 2 b , c , d , e, f представлены возможные варианты такого расширения, которые могут быть следующими:

V Одна экономическая оболочка расширяется в каком-либо месте, а другие две расширяются полностью пропорционально или непропорционально (рис. 2 b ). На основе этого введем величину максимального прогиба экономической оболочки V fne max , которая показывает на сколько может увеличится ее объем, так чтобы она не перешла в экономическую оболочку выше. Это величина приемлема для среднего и малого бизнеса, но не распространяется для случая, представленного на рис. 2 с ;

V Две экономические оболочки расширяются в одном месте, а третья оболочка расширяется пропорционально. Под расширением экономических оболочек в одном месте понимается такое расширение, когда вектор сил, действующий на данные оболочки, лежит на одной прямой, являющейся перпендикуляром к данным точкам. При этом деформация может происходить как на двух соседних оболочках, т.е. экономических оболочках большого и среднего бизнеса (рис. 2 с ) или на оболочках малого и среднего бизнеса. Деформации экономических оболочек могут также происходить и через оболочку, т.е. экономические оболочки малого и большого бизнеса расширяются в одних областях (рис. 2 d ), в то время как экономическая оболочка среднего бизнеса расширяется пропорционально.

• V    Все три экономические оболочки расширяются в одном месте (рис. 2 e );

• V    Две экономические оболочки расширяются в одном месте, а третья в другом месте (рис. 2 f, g );

• V    Три экономические оболочки расширяются в разных местах (рис. 2 h ).

Теперь рассмотрим варианты расширения экономических оболочек, представленные на рис. 3. Как видно из рисунка расширение экономических оболочек можно разделить на два класса: простое расшире- ние, описываемое линейными зависимостями (рис. 3a, b, c, d) и сложное расширение, описываемое степенным, логарифмическим, полиномиальным или другим уравнением (рис. 3e, f, g, h).

На рис. 3 a показаны 2 варианта: когда происходит мгновенное расширение экономической оболочки при воздействии внутренних сил (прямая 1) или же данное воздействие производит столь малое влияние на экономическую оболочку, что ее объем остается без изменений (прямая 2). Этот вариант также возможен при инерционности экономической системы. Но, так как ранее было введено понятие об одноразовом расширении экономической оболочки V en , описываемое уравнением (9), то прямая 1 и представляет таковое (см. также рис. 3 с ). Так как за один раз мгновенного расширения экономическая оболочка, возможно, не достигнет своего значения V fn , то здесь может быть «ступенчатый вариант».

Следующий график на рис. 3 b показывает линейную зависимость, когда экономическая оболочка расширяется прямолинейно под углом к оси абсцисс. Этот вариант является предпочтительным при расширении (сжатии) экономической оболочки, т.к. зная значения угла и время t e можно легко рассчитать конечный объем экономической оболочки.

На рис. 3с, d показаны варианты более сложного развития расширения экономической оболочки, представляющие совокупность двух прямых. Так на рис. 3с изображен случай, когда после воздействия внутренних сил, экономическая оболочка мгновенно отреагировала на это и расширилась на величину Ven после чего происходит изменение ее объема по линейному закону. Рисунок 3d показывает инерционность экономической оболочки после воздействия на нее внешних сил. Инерционность экономической оболочки характеризуется временем tin, в течение которого объем экономической оболочки не изменяется, несмотря на воздействие на нее внешних (внутренних) сил. Инерционность экономической оболочки, показывает, что рынок (фирмы) оценива- ет изменение ситуации и решают вопрос как на нее отреагировать.

Таким образом, здесь можно сделать следующее определение для инерционности экономической оболочки.

Инерционностью экономической оболочки называется такое ее состояние, при котором после воздействия на нее сил Р V ее объем V e не изменяется на протяжении времени At in вследствие осмысливания рынком (фирмами) возможных последствий от них.

Следующий класс изменения объема экономических оболочек представлен на рис. 3 e, f, g, h в виде кривых, которые можно описать общим полиномиальным уравнением.

Так на рис. 3 e показан вариант, когда после воздействия внутренних сил объем экономической оболочки начинает быстро увеличиваться, а потом плавно переходит к своему верхнему значению. Рисунок 3 f показывает аналогичную зависимость, только вначале, после воздействия внутренних сил, объем экономической оболочки изменяется медленно, ввиду инертности системы, а потом изменения происходят по возрастанию.

На последних двух рис. 3 g, h показаны практически одинаковые сложные зависимости изменения объема экономической оболочки. Эти графики имеют точку перегиба с координатами V h и t h , где меняется один вид математической зависимости изменения объема экономической оболочки на другой.

Все три оболочки сжимаются.

В этом случае все силы, действующие на экономические оболочки, направлены снаружи (рис. 4).

При этом могут быть три следующих варианта:

• •    все экономические оболочки сжимаются пропорционально предыдущим своим состояниям по всем осям (рис. 4 а );

• •    все экономические оболочки сжимаются не пропорционально предыдущим своим состояниям по всем осям;

• •    все экономические оболочки сжимаются в одних или нескольких отдельных областях (рис. 4 b ).

На рис. 4 b изображены для наглядности две экономические оболочки, хотя на самом деле V bg = V fn .

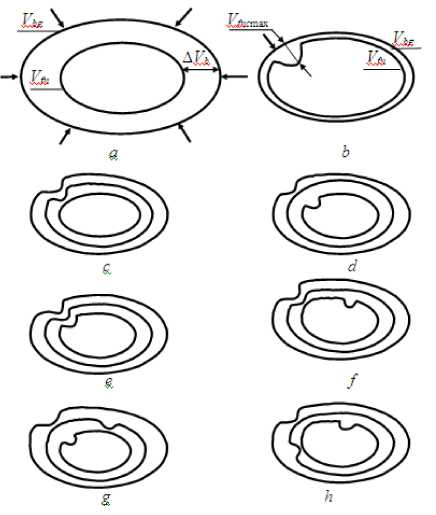
Рис. 4 - Виды сжатия экономических оболочек: а пропорциональное сжатие экономическойоболочки; b сжатия экономической оболочки в отдельной области; V bg начальное состояние экономической оболочки, V fn конечное состояние экономической оболочки, V bnсmax максимальное сжатие экономической оболочки в отдельной области; c , d , e , f, g варианты сжатия экономических оболочек .

Рассмотрим эти сжатия по отдельности:

Пропорциональное сжатие всех экономических оболочек означает, что на них воздействуют равномерно по всей поверхности одинаковые внешние силы. При этом все оболочки сжимаются пропорционально на какой-то определенный процент. По аналогии с описанным выше материалом, введем понятие коэффициента максимального одноразового сжатия K ecc max и период времени, за который это сжатие может произойти t ecc max .

Таким образом, можно записать величину конечного состояния объема экономиче- ской оболочки после воздействия на нее внешних сил (12)

V fn = K ecc max V bg f ( t ecc max ).

Непропорциональное сжатие всех экономических оболочек. При воздейст- вии одинаковых наружных сил на все три экономические оболочки одновременно их реакция будет разной, следовательно, и уменьшение объема этих оболочек будет изменяться по-разному.

Экономические оболочки сжимаются в одной или нескольких отдельных областях. На рис. 4 b , c , d , e , f , h представлены возможные варианты такого сжатия, которые могут быть следующими:

• V    Одна экономическая оболочка сжимаются в каком-либо месте, а другие две сжимаются полностью пропорционально или непропорционально (рис. 4 b );

V Две экономические оболочки сжимаются в одном месте, а третья оболочка сжимаются пропорционально. Под сжатием экономических оболочек в одном месте по- нимается такое сжатие, когда вектор сил, действующий на данные оболочки, лежит на одной прямой, являющейся перпендикуляром к данным точкам. При этом деформация может происходить как на двух соседних оболочках, т.е. экономических оболочках большого и среднего бизнеса (рис. 4с) или на оболочках малого и среднего бизнеса. Деформации экономических оболочек могут также происходить и через оболочку, т.е. экономические оболочки малого и большого бизнеса сжимаются в одних областях (рис. 4d), в то время как экономическая оболочка среднего бизнеса сжимается полностью;

• V    Все три экономические оболочки сжимаются в одном месте (рис. 4 e );

• V    Две экономические оболочки сжимаются в одном месте, а третья в другом месте (рис. 4 f, g );

V Три экономические оболочки сжимаются в разных местах (рис. 4 h ) [4].

Таким образом, основываясь на представленном выше материале, а также создав базы данных и знаний конкретной сервисной компании по кризисам и путям его преодоления, возможно будет прогнозировать и осуществлять различных мероприятий как в предкризисный период, так и во время кризиса, сводя его влияние на компанию к минимуму.