Теоретические исследования характера и условий взаимодействия с забоем тыльных и периферийных конусов шарошек бурового долота со смещенными осями вращения

В настоящее время известны различные подходы, позволяющие оценить эффективность шарошечного бурения, которая зависит от большого количества различных факторов. Их можно разделить на технологические и конструктивные.

Шарошечное долото конструктивно представляет собой породоразрушающий инструмент с шарошками, которые вооружены зубьями и имеют возможность вращаться вокруг собственной оси [1, 2]. В большинстве случаев в конструкциях долот отсутствует смещение осей вращения шарошек относительно оси вращения долота, что позволяет снизить износ вооружения при бурении крепких, твердых и пород средней твердости, а также пород, обладающих повышенной абразивностью [3]. На рис. 1 представлены примеры трёхшарошечного и двухшарошечного долот без смещения осей вращения шарошек. Особый акцент на рисунке сделан на переходе образующих шарошек от периферийных венцов к тыльным конусам, которые являются калибрующими и формируют диаметр и стенки скважины.

Однако такие долота обладают не самой высокой механической скоростью бурения и проходкой на долото при бурении мягких пород. Для увеличения механической скорости бурения при бурении мягких пород используют параллельное смещение осей вращения шарошек, которое позволяет увеличить проскальзывание зубьев вооружения по всей площади забоя [4]. В то время как в большинстве зарубежных компаний в основном используют угловое смещение осей шарошек, которое обеспечивает меньшие величины проскальзывания зубьев, но позволяет увеличить размеры шарошек [5–7].

2022;7(3):231–239

а                                              б

Рис. 1. Варианты конструкций новых (неиспользованных) долот: а – трёхшарошечное долото; б – двухшарошечное долото

Однако анализ износа вооружения шарошечных буровых долот со смещенными осями вращения шарошек после отработки в реальных условиях бурения нефтяных и газовых скважин позволил установить некоторые важные особенности этого процесса [8]. Главной из них является «зализывание» угла, образованного пересечением периферийного основного и калибрующего конусов шарошек (рис. 2). В результате этого процесса происходит увеличение площади «площадки притупления» зубьев периферийных рядов шарошек, что неминуемо приводит к снижению удельного давления на поверхность забоя и, как следствие, снижению разрушающей способности вооружения инструмента [9].

Проведенный анализ износа зубчатого вооружения бурового инструмента в том случае, когда оси вращения шарошек смещены относительно оси вращения долота, позволил установить, что происходит существенное изнашивание («за- лизывание») переходной зоны от тыльного конуса к основному. Интенсивное изнашивание этой поверхности приводит к увеличению площади «площадки притупления» периферийных зубьев шарошки – самой энергозатратной зоны, работающей одновременно как на калибрование, так и на разрушение периферийной области забоя скважины, т. к. именно в этой части шарошки находятся зубья наибольших размеров, формирующие диаметр скважины и, соответственно, испытывающие наибольшие ударные и истирающие нагрузки [10]. Кроме того, это приводит к быстрой потере диаметра долота и, соответственно, диаметра самой скважины.

Повышение эффективности работы шарошечного бурового инструмента, как правило, связано с уменьшением энергетических затрат при бурении за счет обеспечения соответствия геометрии вооружения условиям работы каждого из венцов шарошек на кольцевых участках

Рис. 2. Иллюстрация износа («зализывания») вершин периферийных венцов и тыльных конусов шарошек со смещенными осями вращения

2022;7(3):231–239

забоя и физико-механическим свойствам разбуриваемых горных пород. Таким образом, задача совершенствования конструкции шарошечного бурового инструмента в настоящее время остаётся актуальной [11, 12]. В связи с этим необходимо исследовать причины возникновения указанных негативных процессов при бурении скважины шарошечными долотами со смещенными осями вращения шарошек относительно оси вращения инструмента.

Цель и задачи исследований

Целью работы является повышение эффективности разрушения породы забоя шарошечным буровым инструментом со смещенными осями вращения шарошек на основе проведения теоретических исследований характера и условий взаимодействия с забоем тыльных и периферийных конусов шарошек данного вида бурового инструмента.

Для достижения поставленной цели в работе решены следующие задачи:

• 1.    Анализ характера износа зубчатого вооружения и причин его возникновения у существующих конструкций шарошечного бурового инструмента.

• 2.    Разработка математической модели в цилиндрической системе координат, позволяющей определять расположение и геометрию зоны контакта калибрующего конуса со стенкой скважины для различных типоразмеров шарошечных буровых долот.

• 3.    Разработка компьютерной твердотельной модели для проверки адекватности работы математической модели путём их сравнения.

• 4.    Разработка рекомендаций по дальнейшему совершенствованию конструкции зубчатого вооружения шарошечного бурового инструмента со смещёнными осями вращения шарошек.

Методология исследований

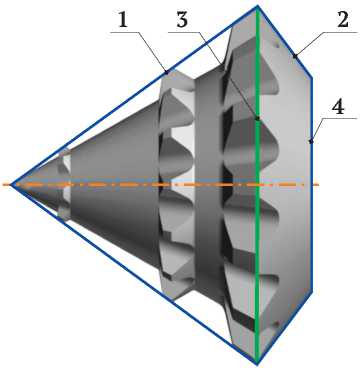
Исследования по определению положения зоны контакта большого основания калибрующего конуса со стенкой скважины были проведены методом математического моделирования геометрических фигур и тел, соответствующих шарошкам и скважине с учетом ряда упрощений и допущений [13]. Так, например, известно, что конструктивно все шарошки буровых долот состоят из корпуса (тела) шарошки и непосредственно вооружения, представляющего собой фрезерованные или твердосплавные зубки. В свою очередь, корпус (тело) шарошки состоит из нескольких сопряженных между собой конусов, которые в общем и целом можно усредненно разделить на два тела: основной и калибрующий конусы, как показано на рис. 3. Таким образом, конструктивно стандартная конструкция шарошки представляет собой сдвоенный конус (основной + калибрующий). Важной особенностью такой конструкции является то, что переходная зона образуется под углом γ = 90° между образующими основного и калибрующего конусов.

Другим упрощением в модели является сама форма моделируемого тела – это основной конус и переходная плоскость θ , являющаяся общей и для основного, и для калибрующего конуса. Эта плоскость представляет научный интерес для исследования, т. к. зона касания со стенкой скважины принадлежит именно ей.

Для математического моделирования применяются методы преобразования координат, составления системы уравнений цилиндра, наклонного конуса и переходной плоскости θ , проходящей через точку их контакта (рис. 4). Для этого на первом этапе было создано геометрическое описание исследуемых тел в цилиндрической системе координат для конуса шарошки без смещения её оси относительно оси скважины.

а

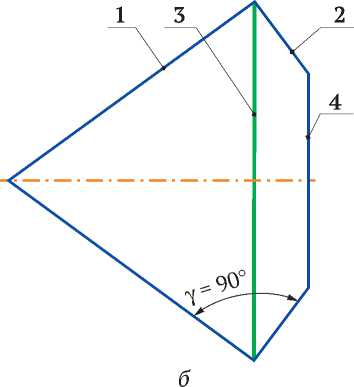
Рис. 3. Упрощение геометрии шарошки перед моделированием: а – модель шарошки с фрезерованным зубчатым вооружением; б – эскиз продольного сечения конусов шарошки;

Как видно из рис. 4, точка М контакта конуса и скважины принадлежит одновременно и стенке цилиндра скважины, и основанию (забою) скважины. Такое положение создаёт идеальный контакт боковой поверхности калибрующего конуса со стенкой скважины, когда «зализывания» периферийных венцов, показанного на рис. 2, не произойдёт.

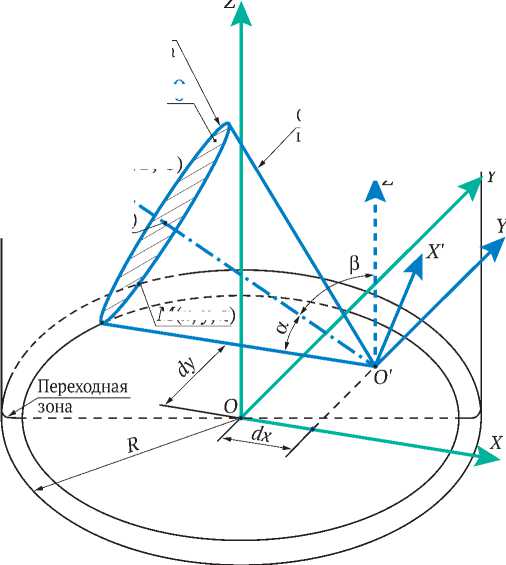
Далее ось геометрической модели конуса смещают вдоль осей X и Y относительно оси геометрической модели скважины на расстояния dx и dy соответственно. При таком смещении оси конуса точка М изменяет своё пространственное положение, смещаясь вверх по стенке цилиндра скважины, и «нависает» над забоем, теряя контакт с ним. При таком положении возникает резкое вдавливание периферийных венцов шарошки в горную породу, в результате чего начинается процесс их сильного износа («зализывания») и формируется округлая переходная зона. В рассматриваемой геометрической модели для определения уравнения конуса и уравнения цилиндра введем две системы координат OXYZ и O'X 'Y 'Z ' (рис. 5).

С учетом параллельного переноса dx и dy и поворота на угол β системы O'X 'Y 'Z ' относительно OXYZ имеем:

x' = (x - dx )cos p + z sin P;

^ У ‘ = У ^- dy ;                           (1)

z ' = z cos p-x sin p.

Задача по нахождению координат точки М была сведена к нахождению точки касания цилиндра, заданного соответствующим уравнением, и конуса, «заваленного на бок» под углом β , с основанием, заданным плоскостью θ .

Уравнение цилиндра имеет вид:

x2 + y2 = R2.

Уравнение конуса в каноническом виде в системе координат O'X 'Y 'Z ' записывается следующим образом:

z x + y z2 = _,              (3)

где с – константа конуса (угловой коэффициент).

Сечение конуса плоскостью OY 'Z ' задается уравнением z = ± cy. Тогда угловой коэффициент прямой сечения с (рис. 6, а ) равен:

c = tg(90 - a) = ctg a.             (4)

Уравнение (3) примет следующий вид:

x '2

,2 Z

У =—г"

ctg2 a

.

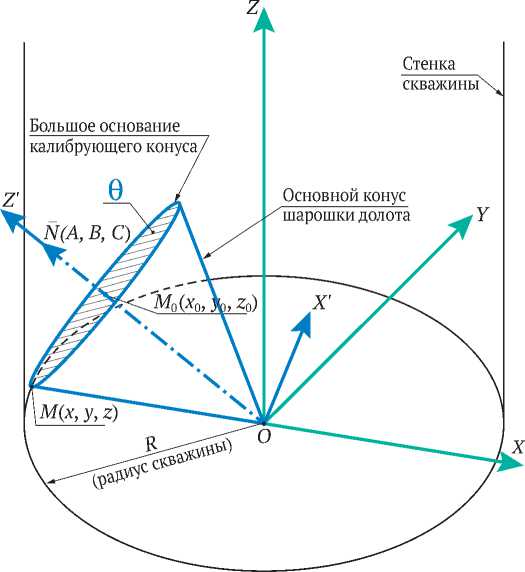
Рис. 4. Геометрическая модель конуса шарошки без смещения оси:

M – точка касания большого основания конуса и скважины; M ₀ – центр большого (переходного) основания конуса

Z

M о ( x о , У o , z o )

Большое основание калибрующего конуса

Стенка скважины

Основной конус шарошки долота

θ

M ( x, y, z )

'

Рис. 5. Геометрическая модель конуса шарошки со смещением оси:

α – угол между O ' Z ' и образующей конуса;

β – угол поворота оси конуса относительно OZ ;

dx – смещение оси конуса относительно OX ;

dу – смещение оси конуса относительно OY

Z '

N(A, B, C )

2022;7(3):231–239

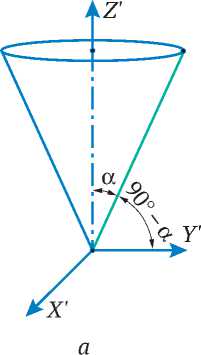
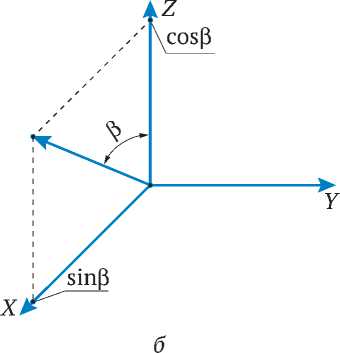
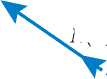
Рис. 6. Геометрическая модель конуса O 'X 'Y 'Z ' :

а – геометрическая модель конуса O 'X 'Y 'Z ' ; б – определение координат нормального вектора плоскости θ ; α – угол конуса

Имея в виду, что:

ctg a

= tg a,

a = 90°-p^ tg(90°-p) = ctg p, (7) и преобразование (1) переноса и поворота, получим уравнение конуса в системе координат OXYZ :

((x - dx )cos p+z sin P)2 + (y - dy )2 = = (z cosp - x sinP)2 ctg2 p.

Плоскость θ , проходящая чере з точку М ₀ перпендикулярно вектору нормали N ( A ; B ; C ), в общем виде задается уравнением:

A( x - x 0) + B (y - y 0) + C (z - z 0) = 0.      (9)

Учитывая то, что нормальным вектором плоскости θ является ось конуса, который получен поворотом отн о сительно оси OY на угол β (рис. 6, б ), получим N (sin P ; 0; cos P ).

Тогда уравнение плоскости θ записывается следующим образом:

sin P( x - x 0) + cos P( z - z 0) = 0.       (10)

Результаты исследований

Таким образом, для нахождения точки М необходимо решить систему нелинейных уравнений:

x2 + y2 = R2;

(x - dx )(cos p + z sin P)2 + (y - dy )2 =

= (z cos p-x sin P)2 ctg2 P;             (11)

sin P( x - x 0) + cos P( z - z 0) = 0.

Полученная система уравнений (11) позволит определять координаты точки М для различных типоразмеров долот при бурении скважин различного диаметра.

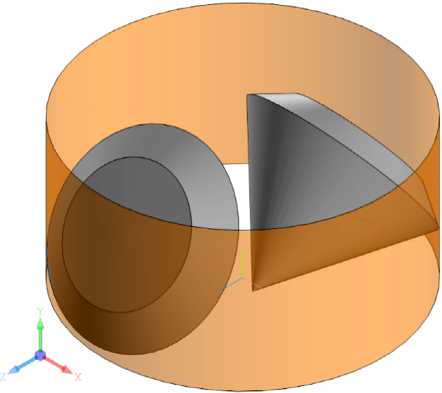
После математического моделирования были построены компьютерная твердотельная модель шарошки, аналогичная её геометрической модели, а также модель цилиндра скважины, с целью проверки сходимости результатов и визуализации искомой зоны контакта. На рис. 7 представлены модели шарошек и скважины, созданные в отечественной системе автоматизированного проектирования КОМПАС-3D.

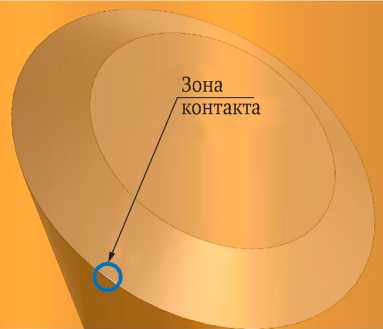
Из рисунка видно, что в твердотельной модели зона контакта калибрующего конуса шарошки определена в той же области, что и математическая. Это свидетельствует об адекватности обеих моделей и корректности полученных результатов.

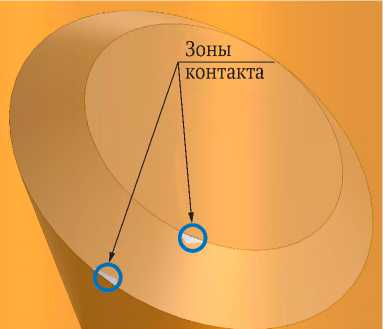
Для минимизации быстрого износа и образования «площадки притупления» в долоте со смещёнными осями шарошек необходимо добиться полного контакта боковой поверхности калибрующего конуса со стенкой скважины, как это есть в стандартных долотах без смещения [14]. Чтобы получить такой контакт, необходимо увеличить угол γ между образующими основного и калибрующего конусов до тех пор, пока малое основание калибрующего конуса не соприкоснётся со стенкой скважины таким же образом и одновременно с его переходной плоскостью θ . Такое положение получено нами итеративным способом в компьютерной твердотельной модели, представленной на рис. 7, г.

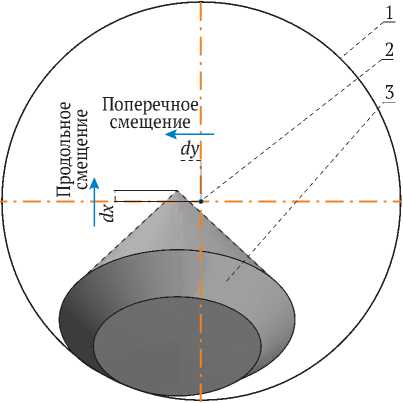
Для достижения такого результата было смоделировано несколько последовательных итераций по увеличению угла γ до значения, которое составило в итоге 97,7913°. Продольное dx и поперечное dy смещения в соответствии со схемой (рис. 7, б ) составили +5,4839 мм и +11,8789 мм и были также определены итеративно. Результат моделирования свидетельствует о том, что искомая геометрия калибрующего конуса может быть определена и математически, аналогично математической модели зоны контакта переходной плоскости со стенкой скважины.

2022;7(3):231–239

а

б

в

г

Рис. 7. Результат 3D-моделирования зоны контакта плоскости θ со скважиной:

а – модель расположения моделей конусов шарошек внутри модели цилиндра скважины; б – схема смещения оси вращения модели шарошки; в – результат моделирования зоны контакта; г – результат 3D-моделирования зон контакта одновременно двух оснований калибрующего конуса со стенкой скважины;

1 – стенка модели скважины; 2 – ось модели скважины; 3 – модель шарошки

За счёт такой конструкции шарошки появится возможность более длительного поддержания требуемого удельного контактного давления для эффективного разрушения породы [15]. Всё это в комплексе позволит увеличить механическую скорость бурения и сохранить диаметр скважины в процессе всей работы буровым инструментом.

Направления дальнейших исследований

Для окончательного достижения цели исследований необходимо определение полной геометрии калибрующего конуса, при которой контакт его поверхности со стенкой скважины будет осуществляться по линии, соединяющей точку М, принадлежащую переходной плоскости θ, и аналогичную точку, принадлежащую малому основанию, координаты которой определяются на основании разработанной математической модели с учетом угла наклона γ. Для этого будет разработана математическая модель, описывающая указанную линию, принадлежащую одновременно и внутренней боковой поверхности цилиндра скважины, и боковой поверхности калибрующего конуса, обеспечивающей равномерное «пятно контакта» (в настоящее время патентуется).

Заключение

Проведенные теоретические исследования позволили установить причины неравномерного износа зубчатого вооружения шарошечного бурового инструмента со смещенными осями вращения шарошек относительно оси вращения инструмента – это несоответствие в полной мере геометрии вооружения долота кривизне стенки скважины в области перехода образующей основного конуса шарошки к калибрующему, а также кинематическим особенностям шарошек со https://mst.misis.ru/

2022;7(3):231–239

смещенными осями вращения относительно оси вращения бурового инструмента.

Разработана математическая модель пересечения плоскости θ переходного основания конуса модели шарошки в области её касания с цилиндром модели скважины, которая позволяет создавать геометрию зубчатого вооружения шарошек, позволяющую существенно уменьшить неравномерность износа зубьев периферийных венцов шарошек и их калибрующих поверхностей таким образом, что при износе вооружения площадь «площадки притупления» зубьев на 15–20 % меньше, чем у вооружения аналогичных стандартных шарошек. Математическая модель была верифицирована путём сравнительного сопоставления с результатами твердотельного компьютерного моделирования, которое показало хорошую сходимость результатов.

Проведённые исследования показали, что необходимо внести существенные коррективы в геометрию зубчатого вооружения шарошек (на данный момент патентуется), позволяющие на 15–20 % уменьшить площади площадок притупления периферийных венцов шарошек, а также обеспечить более длительный контакт основных и калибрующих конусов шарошек с поверхностью забоя и стенки скважины. Это позволит снизить повышенный износ зубьев вооружения в зоне перехода образующей от периферийного основного к калибрующему конусу шарошек и даст возможность зубчатому вооружению шарошек более длительный период времени сохранять требуемое удельное давление на разрушаемую породу, диаметр долота и, как следствие, обеспечит увеличение как механической скорости бурения, так и ресурса бурового инструмента.

2022;7(3):231–239