Теоретические исследования параметров динамической неуравновешенности стирального барабана при отжиме текстильных изделий

Современные стиральные машины барабанного типа отличаются многообразием схем компоновки систем виброизоляции и их конструктивными особенностями. Это приводит к значительному разбросу величин динамических характеристик различных моделей стиральных машин, а также переменных воздействий на подвесную часть, вызывающих не только линейные, но и угловые колебания.

Анализ научных публикаций, посвященных исследованию динамики стиральных машин показал, что практически во всех работах основное внимание уделяется изучению линейных поперечных колебаний подвесной части, вызываемых статической неуравновешенностью барабана, что, очевидно, справедливо, так как этот вид колебаний является определяющим в формировании виброактивности стиральных машин. Однако, в связи с ро- стом значений амплитуд угловых колебаний в современных моделях стиральных машин, определяемых в основном динамической неуравновешенностью барабана, актуальным является необходимость в их исследовании, а также изучении причин, приводящих к ним.

Решение вопросов, связанных с влиянием параметров динамической неуравновешенности стирального барабана на формирование вибрационного поля подвесной части стиральных машин, позволит производить научно обоснованный выбор рациональных параметров системы виброизоляции современных стиральных машин, подверженных активному воздействию угловых колебаний.

Одним из основных факторов, определяющих угловые колебания подвесной части при динамической неуравновешенности стирального барабана, является величина продольного смещения l х центра масс текстильных изделий относительно центральной поперечной плоскости подвесной части, то есть плечо приложения центробежной силы F ц , возникающей от неуравновешенных масс изделий.

В настоящее время вопрос определения величины смещения lх является малоизученным. С точки зрения теоретических аспектов решение данной задачи во многом является взаимоувязанным с процессом поперечного смещения текстильных изделий в барабане при отжиме, то есть, с процессом образования эксцентриситета масс изделий rе, который был подробно рассмотрен в работах [1] и [2]. Однако вопрос определения lх представляет собой более сложную задачу, так как, если при поперечном смещении величина эксцентриситета определяется массой изделий, размерами барабана, центробежной силой и фактором случайного распределения изделий в поперечном сечении барабана, то при продольном смещении величина lх зависит только от массы изделий и размеров барабана, а также от фактора случайного распределения изделий по длине барабана, что значительно усложняет процесс матема- тического описания динамической неуравновешенности.

Решения вопросов исследования случайных процессов, чаще всего, невозможны без принятия обоснованных и необходимых для решения задачи условий и допущений.

Оговорим допущения, которые необходимо сделать перед анализом динамической неуравновешенности барабана.

• 1)    Изделия при отжиме располагаются в поперечном сечении барабана в виде кольца, причем окружность каждой поперечной плоскости внутреннего свободного пространства, образованного изделиями в барабане при отжиме, не может находиться вне оси вращения барабана. (Данное допущение основано на общепринятых теоретических положениях, используемых при рассмотрении процессов центробежного отжима, в частности в [3].)

• 2)    Если размеры кольца, образованного изделиями, различны в поперечных сечениях барабана, то данное изменение размеров кольца по длине барабана описывается линейной зависимостью. (Данное допущение является следствием 1-го допущения, а также основано на результатах опытного наблюдения за процессом распределения изделий в барабане при отжиме.)

• 3)    Плотность текстильных изделий равномерно распределена во всем объеме изделий, находящихся в барабане. (Данное допущение было использовано в диссертации Фетисова И.В. [1], в которой было показано, что при этом погрешности в расчётах незначительны и вполне допустимы.)

• 4)    Боковая поверхность (обечайка) барабана при любой загрузке не может не быть занятой слоем отжимаемых изделий. (Это вызвано относительно небольшими размерами длины барабана в сравнении с его диаметром, а также свойствами текстильных тканей деформироваться под действием нагрузок, изменяя форму изделий и их распределение как в поперечной плоскости, так и по длине барабана.)

  В общем случае при динамической неуравновешенности центральная ось инерции не является параллельной оси вращения и не пересекается с ней. В частном случае динамического дисбаланса центральная ось инерции пересекает ось вращения ротора в точке, отличной от центра тяжести.

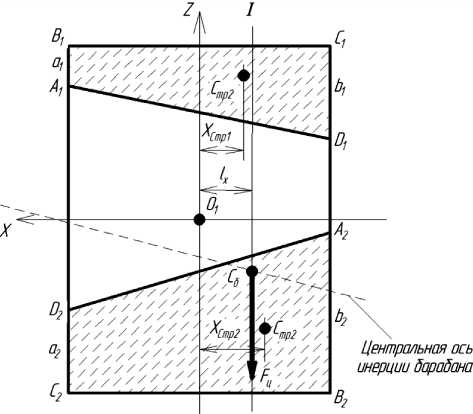
  С учётом особенностей процессов распределения изделий в барабане при отжиме, а также принятых выше допущений, при образовании динамической неуравновешенности в стиральном барабане преобладает в основном такая динамическая неуравновешенность, при которой центральная ось инерции пересекается с осью вращения барабана (рис.1).

  С точки зрения влияния динамической неуравновешенности барабана на виброактивность стиральных машин наиболее актуальным является исследование крайнего расположения изделий по длине барабана, которая характеризуется преобладающим смещением изделий к одной из торцевых стенок барабана (рис.1).

  
  

  _ ³ 1 • x cmp 1 + ³ 2 • x cmp 2

  ¹                                                          ,

  x          3 1 + 3 ₂

  
  
  
  

  где 3 1 и 3 2 - площади трапеций, соответственно, A 1 B 1 C 1 D 1 и A ₂ B ₂ C ₂ D ₂ ; х_Стр 1 и х_{Стр 2} - координаты центров тяжести, соответственно, С_тр 1 и С_тр 1 трапеций A 1 B 1 C 1 D 1 и A 2 B 2 C ₂ D 2 по оси О 1 Х .

  Здесь имеем:

  _ ^L Б ^{( b} 1 ~ ^a 1 )           _ ^L Б ^{( b} 2 ^-a 2 ) .

  ^{Cmp 1}        3b ’ ^{Стр 2}         3 b₂     ’

  
  

  _ ⁽ a i +b1          _ ⁽ a 2 + b 2 )

  ^ 1 -     2    ^L Б ,    ³ 2 -     2

  
  
  
  

  ^L Б .

  
  
  

  /

  Рисунок 1. Схема распределения изделий при динамической неуравновешенности стирального барабана

  
  

  Откуда, после преобразования формула (1) примет вид:

  l L_L b-abM<-^

  x Б 2 b 1 b ₂ ( a 1 +b ₁ + a ₂ + b ₂ ) ,

  Очевидно, что для случая крайнего расположения изделий в барабане при динамической неуравновешенности зна- max чение l x будет максимальным l x  , а па

  раметры b и а , характеризующие неравномерность распределения изделий по длине барабана, будут соответствовать условиям: b —>max и а —»min.

  Исходя из этого и с учётом принятых выше допущений, крайнее положение изделий в барабане будет определяться следующими значениями параметра а : а 1 = а 2 =0,01 м. В свою очередь, если принять b 1 = b ₂, то это будет соответствовать / max , однако эксцентриситет г е приложения силы F_ц будет равен при этом нулю. Поэтому для исследования

  
  

  смещения

  
  

  изделий в крайнем положении

  
  

  будем

  
  

  принимать:

  
  

  D

  b = —    и

  
  

  D

  
  

  Тогда, расстояние l x от центральной поперечной плоскости О 1 YZ до линии действия центробежной силы F_ц может быть определено как координата по оси О 1 Х центра тяжести фигуры, состоящей из двух трапеций A 1 B 1 C 1 D 1 и A ₂ B ₂ C ₂ D 2 , по известной формуле [4]:

  
  

  b = -^ ...0,01 .

  
  

  Здесь значения параметра b ₂ будут зависеть от величины выбранного шага (интервала)

  
  

  D- -0,01

  ^{A b} 2( i ) = —-------

  n_b

  
  

  DE -0,02          .

  -e- -----, где nb =1,

  2 nb

  
  

  2,..., i - количество шагов. Откуда:

  
  

  D Б ( n b  1) +1 0,02

  b 2(1)                                  ;

  
  

  2 n_b

  
  

  _b     D Б ( n b 2) +2 0,02

  b 2(2)

  
  

  изделий при различных вариациях геометрических параметров стирального барабана.

  
  

  2 n_b

  
  

  D Б ( n b   i ) + i 0,02

  ^b 2( i )

  
  

  2 n_b

  
  

  .

  
  
  
  

  Для исследования параметров динамической неуравновешенности барабана будем учитывать диапазоны значений диаметра стирального барабана современных стиральных машин D Б , длины барабана L Б и коэффициента длины бара- L

  бана k     ^Б , которые находятся в сле-

  D Б

  
  

  длина барабана, м

  

  0,16

  0,14

  0,12

  0,1

  0,08 длина lx, м

  0,06

  0,04

  0,02

  £8.

  
  

  к-т длины барабана

  
  

  дующих D Б =0,40…0,52 k L =0,25…0,6.

  
  

  интервалах

  
  

  значений:

  
  

  м;   L Б =0,12…0,28  м;

  
  

  Определим в принятых выше диапазонах значений геометрических параметров барабана и параметров а и b , определяющих неравномерность распределения изделий по длине барабана, зна- max

  чение l_x   приложения сил по формуле

  Для этого предварительно найдём значения параметра b 2 , приняв количество шагов n b =4. Тогда:

  
  

  диаметр барабана, м

  
  

  а) b 2(1)

  

  0,14

  0,12

  0,1

  0,08

  длина lx, м

  0,06

  0,04

  0,02

  5П

  
  

  к-т длины барабана

  
  

  ^b 2(1)

  
  

  3 D + 0,02 Б

  
  

  ^b 2(3)

  
  

  8 D + 0,06

  
  

  ; b 2(2)

  
  

  2 D + 0,04

  
  
  
  

  ;

  
  

  0,08

  ; b 2(4)             0,01

  
  

  м.

  
  

  б) b 2(4)

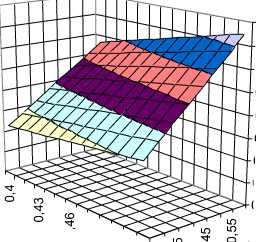
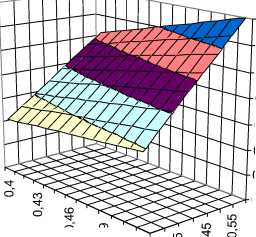
  Рисунок 2. Графики поверхностей значений смещения l_x ^max в зависимости от диаметра барабана D Б и коэффициента длины

  D

  барабана k при b =0,5 D , b      ^Б ...0,01

  2₂        )

  и а 1 =а 2 =0,01 м

  
  

На рис.2 показаны графики по-

верхностей значений смещения lxmax в зависимости от диаметра барабана DБ и коэффициента длины барабана kL при D .  .            _ b1=0,5DБ, b2      Б ...0,01 и а1=а2=0,01 м.

max

Так как здесь разница значений lx   при b2(1), b2(2) и b2(3) оказались незначительной, то на рис. 2 показаны только два графика: а) при b2(1) и б) при b2(4).

Принятые выше условия исследования, при которых параметры b1=0,5DБ, b      Б ...0,01 и а1=а2=0,01 м, преду сматривают изменение значений массы mб≠const и объема Vб≠const отжимаемых

Рассмотрим, как изменяются значения смещения l_x ^max в зависимости от диаметра барабана D Б , коэффициента длины барабана k L при максимальной неравномерности распределения изделий по длине барабана ( b 1^max и а min) и при условии постоянства массы m б =const и объёма V б =const отжимаемых изделий.

Для определения параметров а и b необходимо знать объём Vв внутреннего свободного пространства, образованного изделиями при отжиме, который имеет вид наклонного усечённого конуса (рис.1). Так как основаниями данного конуса являются круги, а его высота не совпадает с осью конуса, соединяющей центры оснований, то данный усечённый наклонный конус является круговым, в отличие от круглого, в котором высота и ось совпадают.

Объём V_e такого конуса вычисляется по следующей формуле:

V_g = 1 LБ_Б ( d^ + d ₂ ² + d_x d ₂ ),    (6)

где d i и d ₂ - диаметры оснований усечённого конуса, соответственно, верхнего и нижнего (в данном случае правого и левого).

С учётом d ₁ = D Б -( b ₁ + b ₂ ); d ₂ = D Б — ( а ₁ + а ₂ ) формула (6) примет вид:

• У_в= - l L_b {[ DБ -( b i + b 2 )] ²+ ...

... + [ DБ-(ai + а 2)]2+...(7)

... + [DB-(bi + b2)][De-(ai ^a2)]}, или

V ₌ D {3 D [ D _ ( b b ) _...

в        J       I E E       i2

...-(ai + a 2)] + (bi +b2)2 +(ai + a 2)2 +....

... + (bi +b2)( ai + a2)}(8)

Так как  Ve = Ve — Vd,  где

DDk

-^ L_B = —- ^—L - объём барабана; V₆ -объём, занимаемый отжимаемыми изделиями в барабане, то будем иметь:

3 D 2-- б— = 3 D_e ( D_R-b b -a a. ) + ...

E             EE   i   2   i   2

kLDБ

... + ⁽ b i + b 2 ^{) 2} +^{( a} i + ^a 2 ^{)2 +} — ... + ( b_i + b ₂ )( a _i + a ₂ ).

Значения a 1 и a ₂ для обеспечения максимальной неравномерности примем минимальными: a _i = a ₂ =0,01 м.

Используя методику расчёта возмущающих сил и их компонент при отжиме, приведённую в [2], получим при загрузке барабана т бо =2 кг сухими текстильными изделиями объём отжимаемых изделий: V 6 =0,01209 м³.

По формуле (9) определим параметр b2. Затем, используя полученные данные, рассчитаем значение смещения /max по формуле (4).

На рис.3 показаны графики зави- max симости смещения /x

от коэффициента

k_L при различных значениях диаметра D_E и постоянном объёме изделий V₆ =const ( b i =0,5 D_e , b ₂ ^const и a _i =a ₂ =0,01 м).

На рис. 4 показаны графики зави- max симости смещения lx от диаметра DE при различных значениях коэффициента kL и постоянном объёме изделий V6=const (bi=0,5De, b2^const и ai =a2=0,01 м).

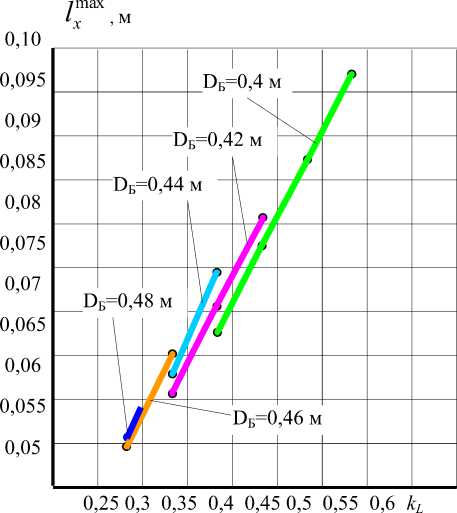
Рисунок 3. Графики зависимости смеще-max ния lx   от коэффициента kL при различ ных значениях диаметра DE и постоянном объёме изделий V6=const (bi=0,5DE, b2^const и a i =a2=0,01 м)

В связи с тем, что при исследовании было принято значение массы загружаемых в барабан текстильных изделий, равное mбо=2 кг, то для некоторых значений геометрических параметров барабана толщина слоя изделий, распределённых по его обечайке, принимала значения менее 0,01 м, что не соответствует принятым условиям исследований. Поэтому, в определённых интервалах значений диаметра барабана DБ и коэффициента kL ряд функций, приведенных на рис.3 и 4 не существует.

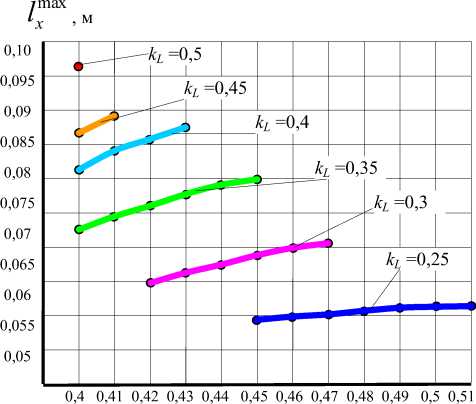
D _Б , м

Рисунок 4. Графики зависимости смеще-max ния lx  от диаметра DБ при различных

значениях коэффициента k L и постоянном объёме изделий V б =const ( b 1 =0,5 D Б , b 2 ≠const и а 1 =а 2 =0,01 м)

Анализ графиков на рис.2, 3 и 4 показывает, что значения смещения l ^max растут при увеличении диаметра барабана D Б и коэффициента длины барабана k L . Причем, наиболее значимый рост наблюдается при увеличении k L .

Соотношение между величиной lmax и длиной барабана LБ во всем диапа-max зоне D составило x =(0,434…0,49). LБ

Отметим также, что значения l ^max увеличиваются при b 2^ 0,5 D Б (или b 2^ b 1 и при b 1 max).

Таким образом, установлено, что продольное смещение центра масс изделий при отжиме в барабане не превышает половины длины барабана, однако в крайнем положении может находиться вблизи одной из торцевых стенок бараба- на.

Полученные данные показывают, что путём варьирования геометрических параметров барабана и, в первую очередь, коэффициента длины возможно, возможно влияние на величину момента сил, действующего на подвесную часть стиральных машин при угловых колебаниях, вызванных динамической неуравновешенностью барабана.

Полученные результаты работы могут быть использованы при выборе рациональных конструктивных параметров стиральных машин барабанного типа, обеспечивающих снижение их виброактивности при отжиме.