Теоретические исследования процесса отжима сока шнековым рабочим органом с дополнительным дренирующим контуром

Введение. Шнековые прессы являются наиболее распространённым отжимным устройством непрерывного действия в технологии влажного фракционирования [1]. В таких прессах возможно достичь давление, необходимое для обезвоживания зелёной массы. Эффект самодозирования шнековых прессов исключает необходимость равномерной подачи материала. Однако вследствие большой толщины прессуемого слоя и сравнительно малой площади контакта обезвоживаемого материала с дренирующим контуром шнековые прессы обладают меньшей в сравнении с другими устройствами степенью обезвоживания.

С целью повышения качества отжима предложена конструкция шнека с дополнительным дренирующим контуром [2, 3] (рис.1). Для теоретической оценки эффективности разработанной конструкции составлена математическая модель, позволяющая рассчитать выход сока в процессе механического обезвоживания.

Рис.1. Конструкция шнекового рабочего органа с дополнительным дренирующим контуром: 1 – канал; 2 – отверстия

Расчёт скорости фильтрации сока при отжиме. Для описания процесса фильтрации зелёного сока через пористую среду растительного скелета воспользуемся законом Дарси [4]:

где vx, vyvz _ . дH Vx     x дx дH 1 vy =-ky      ,                                           (1) дy , дH vz =— kz ' — I z      z дz – скорости фильтрации жидкости в направлениях x, y, z соответственно; kx, kykz — коэффициенты фильтрации жидкости в направлениях x, y, z соответственно;

d H d H d H d x ’ d y ’ d z

– падение напора на единицу длины в направлениях x, y, z соответственно

(градиенты порового давления).

Межвитковое пространство шнека представлено в виде трапецеидального жёлоба (рис.2):

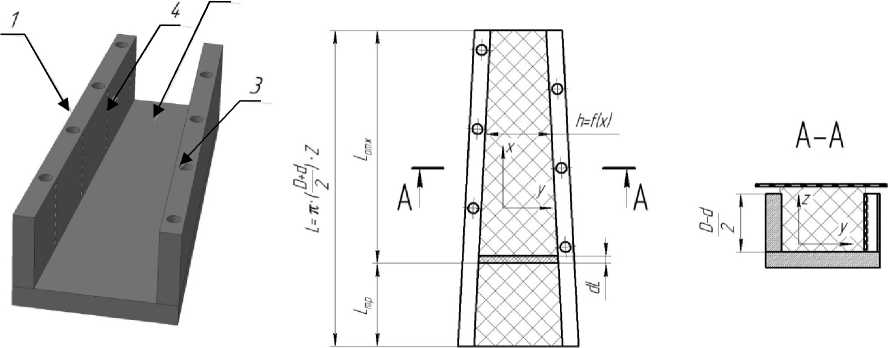
Рис.2. Модель развёрнутого межвиткового пространства шнека:

1 – виток; 2 – вал шнека; 3 – канал дополнительного дренирующего контура; 4 – отверстия; D и d – внешний и внутренний диаметры шнека; Z – количество витков шнека

Разобьём объём межвиткового пространства на конечное число элементарных слоёв, толщиной dL . Применительно к модели шнека с дополнительным дренирующим контуром закон (1) приобретает следующий вид:

^v i y =

—.

Ч z =

—

,  d H

" ky о y

, dH k_z-- ^z d z

.

При фильтрации через фильтрующую перегородку изменением давления внутри прессуемого слоя можно пренебречь. Интегрируем каждое уравнения системы (2).

Для направления по оси y (начальные условия y = 0, граничные условия – длина участка фильтрации равна ширине канала y= h ), для направления по оси z (начальные условия z = d ,

D граничные условия z = —) получает следующие зависимости:

^v i y = k y ■

v = к ■ 1 z z

H — C 1

h

2 ■ ( H — C ₂ )

.

( D — d )

При отсутствии порового давления, H = 0, скорость фильтрации равна нулю v1 y = 0, v1 z = 0. Таким образом,

C 1 = 0 ;          C ₂ = 0 .

Уравнение (3) приобретает вид:

H

’ y = k y ^- h

= kz -

2 H

( D - d )

v 1 z

Скорость фильтрации одновременно в двух направлениях рассчитывается по общеизвест-

ному свойству градиента:

22 V 1 = V V 1 У + V 1 z ;

2 H

.

+ kz • V

^V 1 =

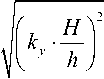
( D - d ) J

Скорость фильтрации сока во всём канале будет определяться как сумма скоростей каждого слоя на участке 0 - L_оmж . В дифференциальной форме зависимость будет следующей:

Lотж .’ -hl L H)   ,   2 H     , V ky-h И kz'( D - d )J x ,                           (6) отж 2H , ’z- | kz-D-d) -x где v – скорость фильтрации жидкости при отжиме экспериментальным шнеком (фильтрация в направлениях y и z); vz – скорость фильтрации жидкости при отжиме стандартным шнеком (фильтрация в направлении z).

Для расчёта скоростей фильтрации на всём участке отжима сока L_отж представим все зависимости, входящие в уравнение (6), от координаты x . На рис.3 представлена зависимость ширины канала h от координаты x .

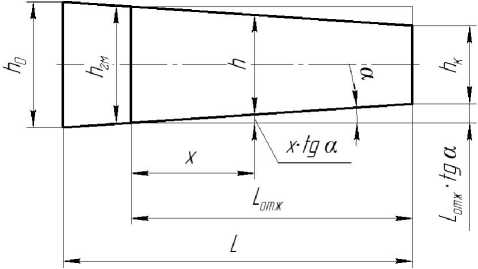
Рис.3. Геометрические параметры межвиткового пространства шнека

Толщина межвиткового пространства (канала) h в любой точке будет определяться соотношением:

^h = h о ^- 2 ^{- (} x + L_m p ) ^- tg a | L" .                                    (7)

Найдём величину tg a . Отношение начальной толщины канала h ₀ к конечной толщине h_K является коэффициентом сжатия материала k_сж :

-г = кеж .                                             (8)

h _к

Согласно зависимости (8) конечная толщина канала: h_K = h 0 - 2 L • tg a .

Подставим данную зависимость в уравнение (8):

откуда

h ₀

h ₀ - 2 L • tg a

k сж ,

tg a = h о

k сж

- 1

2 L • k ..

сж

Формула (8) с учётом (10) приобретает вид:

h = h ₀

1 — ( X + L mp ) •

V

к сж

- 1

L отж

L • k сж

Ширина канала в середине участка отжима равна

x = 0

("ж hue = h о 1 - (/ + Lmp) • -ж— I    .

^{V       2             L} • ^-сж J X = 0

Поровое давление, входящее в уравнение скорости фильтрации сока (6), является составной частью общего давления [6]:

P = Н + E ,(12)

где P – полное давление на прессующую поверхность витка шнека в направлении прессования;

H – поровое (нейтральное) давление; E – эффективное давление.

Эффективное давление определяется из условия равновесия выделенного элементарного объёма обезвоживаемого материала. Оно определяется следующим выражением:

Г _ Г , - a ^{( L} X )

E  ^Е вых e

L отж _.

I X = 0

При условии, что на выходе из прессующей камеры Е_вых = Р_вых ,

Г¹ _ о _ф - a ^{( L}omx

^Е Р вых e

L отж ^х )            ,

X = 0

где Р_вых – общее давление на выходе из прессующей секции; a – расчетный коэффициент. Осевое давление E связано с радиальным E ^рад следующим законом:

рад

=^ .

E

Для описания порового давления примем следующую зависимость:

Н = Нм • e-ah •(х-Lmp), где Hгм – поровое давление на этапе достижения состояния гидромассы; ah – эмпирический коэффициент.

Поровое давление H_гм свяжем с эффективным давлением на этапе достижения состояния гидромассы E_гм следующей зависимостью:

Нм = bh • Егм, где Егм определяется зависимостью (13) при х = 0 ; bh - эмпирический коэффициент.

Исследования [5] показали, что взаимосвязь осевого и радиального поровых давлений целесообразно описывать уравнением:

Н- = Hy- =_t .

H рад   H _z

Конечная зависимость поровых давлений H _y и H _z от положения в прессовом канале, исходя из (15), имеет вид

<

Н = Н  ^l-e- ahX y      гм

Н = Н • e ^{- a} h ^X z       гм

L отж

.

X = 0

Определение коэффициента фильтрации зелёного сока через «скелет» растительной массы подробно рассмотрено в работе В.Н. Фомина [1]. Начальный коэффициент фильтрации (в момент достижения материалом состояния гидромассы) определяется зависимостью:

k_{ф 0}

r    Y зс • H в

= 4 a

Y в • H зс

•

a 10

V

— Оц

Y c —

Y в

1 -

Y Л ^C- - C )

b 4

^Y sm • ( ^Csm - ^Cj H¹ - x * )    ,

где £ _a - коэффициент соотношения продольной и поперечной фильтрации;

к ф = ^ a • к ф

Y _зс , Y в — плотность зелёного сока и воды соответственно; ц в , ц _зс - коэффициент вязкости зелёного сока и воды соответственно; a ₁₀ , a_u , b 4 - эмпирические коэффициенты; у _e , у _c = у _e • C e -объёмная плотность измельчённой зелёной массы и сухого вещества измельчённой зелёной массы соответственно; C_e , C _j – содержание сухого вещества в измельчённой зелёной массе и зелёного сока; у _sm - объёмная плотность максимально деформированной измельчённой зелёной массы; C_sm – содержание сухого вещества в максимально деформированной измельчённой зелёной массы; x _* – относительная линейная деформация.

По аналогии с зависимостью изменения коэффициента пористости [4] примем следующую модель изменения коэффициента фильтрации:

к ф = к ф о ' ( 1 - а . • Р .ых • e""' L" - x ) ) I L =0 ,                            (21)

где a_k – эмпирический коэффициент.

Полученные зависимости подставим в систему уравнений скорости фильтрации сока (6):

v =

L отж

J

- a •(- - x))HM ‘^‘e ф0y (1 a. P вых e )         ,

V                                                 ^h IIс

+

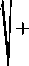
^к ф 0 z •(¹ - « к^вых V

• e ^a '^{( L} °m^ x )

2 Н гм- e

ah- x 1

• dx

( D — d ) J

^Lотж                                                     T T - aa h • X

V, = J к ф 0 z -( 1 — a .' P.. .'e~ ^a ' ^{( L}- - x ) ) •          ,Z • dx

^       0                                     ⁽ D d )

Произведём интегрирование при помощи математической программы Wolfram Mathematica 7.0:

L отж

a at-ea• L°”"-ah-ea• L°”" A-ah-a -eax P h                h к           вых v = x

e ah- x

(H

• a a •⁽ x - Lom^ ) • Ы

• p Л вых

4 k_{ф 0 z}

—

₊ к^

.

vz

( a h ( a h ^— a ) • ( e a^ тж ^— a .

ah x e       ф0z    гм

—

гм

, a • x

e

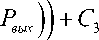
, a • ( ^{X —} L om^ ) , p

1     a_K • e

• — + —

1 вых

\

L отж

x = 0

V a h

a ^— a h

D — d

—+ c ₄

t x = 0

Для вычисления констант С ₃ , С ₄ рассмотрим состояние в начале процесса отжима после достижения материалом состояния гидромассы. В этот момент сумма скоростей (23) будет равна скорости фильтрации этого элементарного участка (22) при x = 0 .

Окончательный вид суммарных скоростей фильтрации сока. Для экспериментальной кон- струкции шнека:

v = ( a • e a • ^L™

—

a • ea• Lom" + a a  e»• ьотж • p ) x к             вых

X

e

,^—2 a L-ж-1 h _{— a} • h -p V •

⁽ гм    a k     гм ¹ вых )

( ah ( ah

— a ) • ( e a • L ^OT"

—

4 k ф ²0 z

к ( D — d ) 2

a • L й к • e

+

2 _S2 к ^кФ 0 У ^

h

—

IIс

( a • e^a • ""

—

a. • L a h • e

⁺ a h

•a P V (H к вых           гм

—

_a . _e - a • L^om". н p V • к                 гм вых

^{4 k}ф ²0 z

—

( ah ( ah

— a ) • ( e a L ^OT"

—

a. • L й к • e

+

к кФоу-(1

—

a • P • e к вых

■ a ■ ( L OT" ) ) •

Нгм Л

h IIс

^{+ к}ф 0 z "(1

—

a • P • e к вых

к

k ( D — d ) ²

— a •

⁽ L OT" ) ^ ^

+

^кф о У -^² к

2 H гм

h

IIс

+

( D — d ) 7

Для стандартной конструкции:

vz

7 p ^ah • L orn" . 7,

² e        ^кф 0 z

—

• Нгм'     +

к a h

D — d

a P к вых

a

к

—ah 7 +

+кфоz •(1—

a • P к вых

• e

,^— a •⁽ L OT" ) ) •

2 H гм

k ф0z

• H.     + a k^ e

гм

1 a • L OT" • p вых

к

.

(D — d)

+

к a h

a

— a_h

7

D — d

Масса сока, вышедшая при отжиме зелёной массы, занимающей

объём

межвиткового пространства прессующих витков, равна [7]

М ЗС = v • ( F ,+ F 3 )'P t ”""

,

М ЗС = v z • F ₃ T t "

,

где Fз , Fо.в. – эффективные площади зеерной камеры, контактирующей с отжимаемым продуктом и площадь дополнительного дренирующего контура соответственно; у - объёмный вес зе- лёного сока; tотж – время отжима через зеерную камеру.

Исходя из зависимости (10), эффективная площадь зеерной камеры, контактирующей с отжимаемым продуктом, равна

L отж

F 3 = F 3.C/ J h 0 1 — ( ^ + L mp ) • "^c"₁^—- I , Lkew

0                           сж

F з

= F³

ж с

L-L -(2L-L 4k 0 отж         отж сж

2 L • ^

сж

где F _ж ^з _с – живое сечение зеерного цилиндра.

Площадь дополнительного дренирующего контура равна

F = d^{д,^}'^k ■ j ■ i,                                                 (28)

о в отв , где dодтдкв – диаметр отверстий дополнительного дренирующего контура; j – количество отверстий в ряде; i – количество каналов.

Время отжима сока запишем в виде отношения пройдённого пути элементарным слоем материала к скорости прохождения:

t отж

L отж V ^,

где V – линейная скорость витков шнека по среднему диаметру:

п-n D + d п- n , V =---=--( D + d ) ,

30    4    120

n – число оборотов шнека.

Уравнение (29) принимает окончательный вид:

t отж

120 • L отж

п- n • ( D + d )'

Определяем выход сока:

X =

X z

M ЗС

ЗМ , отж

M ЗС z

M ЗМ , отж

где M _о ^З _т ^М _ж – масса измельчённой зелёной массы, занимающая объём межвиткового пространства прессующих витков, до прессования (т.е. в состоянии гидромассы):

М ЗМ = V ^3M     ,

отж отж   г .м. , где VоЗтМж – условный объём зелёной массы в зоне отжима сока при одинаковой плотности массы;

p „ - плотность гидромассы. г . м .

Условный объём, занимаемый зелёной массой при одной плотности, рассчитаем как пло- щадь поперечного сечения канала в месте достижения материалом состояние гидромассы на длину жёлоба L:

V ЗМ отж

D - d

- h о -

Г           -1^

сж тр _T 1 I отж .

I L - кж J сж

Окончательные уравнения, позволяющие рассчитать выход сока, после соответствующих преобразований:

X = v -

120 - ( 2 L - к ж - d ^ - j - i + F ;, с . h о - Ь отж • ( 2 L - Ь отж • ( к ж - 1 ) ) ) - _Y ^{n- n -} ( ^{D 2 - d 2} ) ^- h о ^- ( ^L + ^Lоmж • ^{( к}сж ^{- 1)}) ^{- p} _г . м .

з ж. с.   отж \        отж \ сж )) < п - n - (D2 - d2) - (L + L - (к -1)) - p отж сж           г . м .

Заключение. Получена математическая модель, позволяющая рассчитать выход сока, отводимого из камеры прессования одновременно в двух направлениях: в направлении зеерной камеры и дополнительного дренирующего контура в витках шнека.