Теоретические исследования взаимосвязи степени турбулизации потока с коэффициентом теплоотдачи

• -    раскрыть взаимосвязи коэффициента теплоотдачи со степенью турбулизации потока;

• -    исследовать математически влияние дополнительной турбулизации потока на коэффициент теплоотдачи от греющего теплоносителя к стенке трубы;

• -    описать физический процесс теплоотдачи.

Методы исследования . Анализ литературных источников по теплотехнике и гидравлике, математические вычисления коэффициента Кориолиса, сравнение способов характеризации степени турбулизации потока по скорости потока (по числу Рейнольдса) и при внесении в поток устройства, усредняющего скорости по сечению при том же числе Рейнольдса.

Коэффициент теплопередачи в водо-водяном теплообменнике «труба в трубе» в основном зависит от коэффициента теплоотдачи αг от греющего теплоносителя к стенке трубы. Физический процесс теплоотдачи состоит в следующем. При ламинарном режиме движения жидкости, то есть при числе Рейнольдса Re < 2320, эпюра скоростей имеет параболическую форму. Эпюра температуры имеет аналогичную форму [3]. В этом случае температура, имеющая максимальное значение в центре трубы, распространяется к стенкам за счет теплопроводности, и у стенки имеется минимальное значение. Эпюра турбулентного режима движения (Re > 4000) имеет форму усеченной параболы. Однако у стенки трубы имеет место тонкий подстилающий ламинарный слой, через который тепло к стенке также распространяется за счет теплопроводности. Поэтому для увеличения коэффициента теплоотдачи необходимо разрушить этот подстилающий ламинарный слой и получить эпюру температуры в виде прямоугольника (рис. 1).

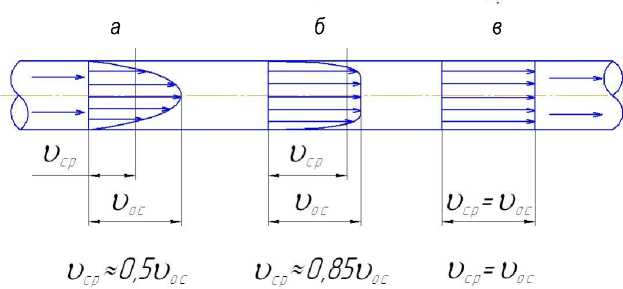
Рис. 1. Эпюры температур по сечению трубопровода: а – ламинарное движение;

б – турбулентное движение; в – искомое движение для максимальной теплоотдачи

В этом случае можно ожидать, что в формуле теплопередачи термическое сопротивление теплоотдачи от греющего теплоносителя к стенке трубы можно исключить. Тепловой поток определяется

Q =k•F• Lt, Вт, где k - коэффициент теплопередачи, Вт/(м-К), к =---------;

г +Я л + R нн

R αг – термическое сопротивление теплоотдачи от греющего теплоносителя к внутренней поверхности стенки трубы, (м∙К)/Вт;

R л - термическое сопротивление стенки трубы, (м-К)/Вт;

R αн – термическое сопротивление теплоотдачи от наружной поверхности стенки трубы к нагреваемому теплоносителю, (м∙К)/Вт;

• F – площадь поверхности теплообмена, м²;

Δ t – разница температур между греющим и нагреваемым теплоносителями, ˚К.

Коэффициент теплоотдачи α г функционально связан с критерием Нуссельта Nu

Nu-Л

^ =-

где Nu – число Нуссельта;

Л - коэффициент теплопроводности жидкости, Вт/(м-К);

d – диаметр трубы, м.

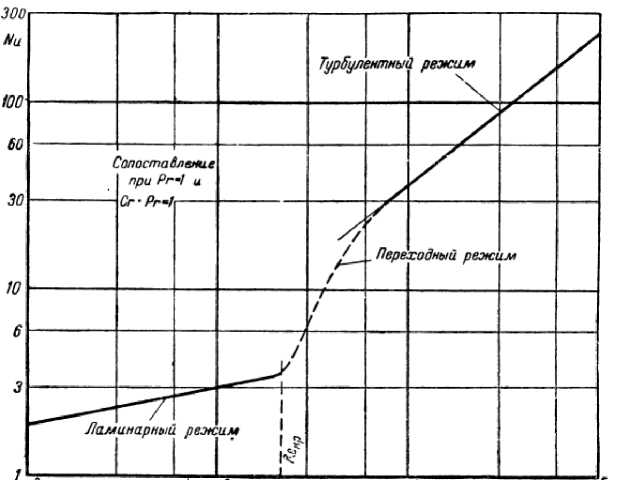
Критерий Нуссельта, в свою очередь, связан с числом Рейнольдса (рис. 2) [3]. Характер кривых свидетельствует, что с увеличением числа Рейнольдса Re увеличивается критерий Нуссельта Nu , а значит, и коэффициент теплоотдачи α г .

При ламинарном движении, когда теплоотдача от греющего теплоносителя к стенке определяется теплопроводностью, критерий Нуссельта имеет минимальное значение. С увеличением скорости при турбулентном режиме ( Re > 4∙10³) критерий Нуссельта возрастает более интенсивно, а значит, возрастает и коэффициент α г . Это свидетельствует об уменьшении подстилающего ламинарного слоя, причем критерий Нуссельта увеличивается по логарифмической кривой.

Ю² 3    6 ' 10³       3     6            3 6~ir

Рис. 2. Взаимосвязь критерия Нуссельта с числом Рейнольдса при Pr = 1 и Gr∙Pr = 1

При проектировании теплообменников мы ограничены скоростью движения теплоносителя в трубах отопления, в которые может быть вмонтирован теплообменник. Эта скорость находится в пределах 1,0–1,5 м/с, а в теплообменнике, трубопровод которого может быть большего диаметра, скорость будет в пределах 0,4–0,6 м/с. Число Рейнольдса в этом случае будет в пределах (1,0– 1,5)∙104, эпюра температур будет в виде усеченной параболы. Для перевода формы эпюры температур из усеченной параболы в прямоугольную (рис. 1, б, в) необходимо разрушить подстилающий ламинарный слой.

На практике встречаются устройства, решающие эту задачу механическим способом. Если гладкую трубку с греющим теплоносителем изогнуть в виде спирали, коэффициент теплоотдачи α из увеличивается на коэффициент α R [3], то есть

П из = Rr ' П-ямям, где αиз – коэффициент теплоотдачи изогнутой трубки, Вт/(м2∙К);

a r - поправочный коэффициент , a _R = 1 + 1,77 ^ ;

R – радиус змеевика, м;

d – диаметр трубы, м;

α прям – коэффициент теплоотдачи прямой трубы.

В дымогарных трубах парового котла Д721-А для увеличения теплоотдачи установлены изогнутые в виде винтовой поверхности полоски металла. Подобные «турбулизаторы» устанавливаются в трубках радиаторов современных автомобилей. Эти устройства позволяют до 1,5 раза увеличить теплоотдачу от греющего теплоносителя к стенке трубы. Также увеличивается коэффициент теплоотдачи, если на трубках выполнить зиги (рис. 3) [4].

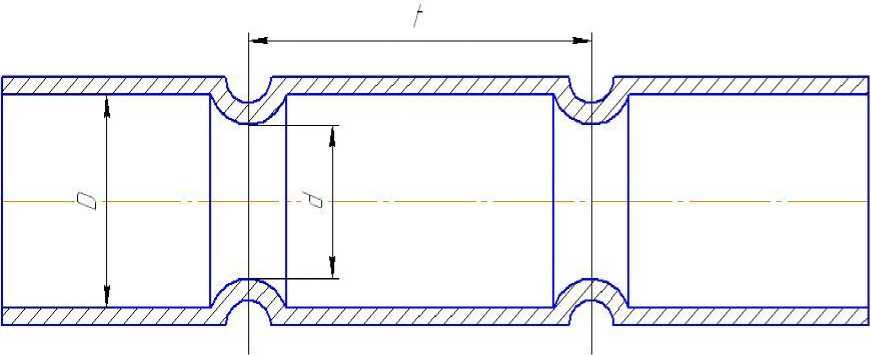
Рис. 3. Продольный разрез трубы с зигами на наружной стороне и плавно очерченными выступами внутри

В рассмотренных случаях дополнительная турбулизация потока позволяет при данном значении числа Рейнольдса увеличить значение критерия Нуссельта, а значит, и коэффициента теплоотдачи. Дополнительная турбулизация потока есть не что иное, как усреднение скоростей потока по сечению трубы, а значит, способствует разрушению подстилающего ламинарного слоя у стенки трубы.

Рассмотренные способы турбулизации образуют большую степень турбулизации, однако поток в какой-то степени становится установившимся, а значит, не может окончательно разрушить подстилающий ламинарный слой.

Неравномерность распределения скоростей по сечению определяется коэффициентом Кориолиса акор [5]

кор     Екр а        ЕсP, где Ер = J u3dwp t - кинетическая энергия потока, подсчитанная при реальной скорости как сумма кинетических энергий всех элементарных струек;

Е с ^р = и³ ш р t - кинетическая энергия, подсчитанная для средней скорости потока;

ш - площадь сечения потока, м2;

и - средняя скорость потока, м/с;

u = f (ш) - скорость элементарной струйки, м/с.

Для вычисления коэффициента Кориолиса следует взять интеграл

Е^р = J u³d w^p t.

кω

Эпюра скоростей при ламинарном режиме имеет форму параболы (рис. 4). Уравнение параболы: у = ах².

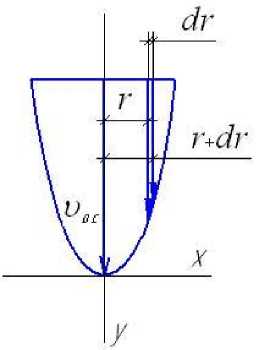
Рис. 4. Эпюра скоростей при ламинарном режиме движения

Определим осевую скорость по рисунку 4

V ос = a R2, где R - максимальный радиус параболы, м; а = ^ос, тогда

У = ~х ² .

R2

Возьмем элементарную кольцевую струйку с радиусами r + dr, тогда dw = т[[(г + dr)2 — r2 ] = nr2 + 2rdr + dr2 — r2.

Исключив из рассмотрения как малую величину dr2, получим dw = 2nr dr.

С учетом вышеприведенных преобразований интеграл будет иметь вид

,                                  R

(^ _r 2 ) 2_nrdr = 2УО ^R_rd dr= 2^ 0 ■—I = ² — °^{cR 8} = —^v°^c

.

^J R²                      R 6 J o             R 6    ₈ I          8 R⁶         4

Таким образом

Е р = J u³d w p t =

nlpVoc ^pt _ ЫУ о с ^p_f.

4    2        4  2 ’’

и коэффициент Кориолиса

а кор =

E K^P = w³ w p t,

Ер _ (даос _    V ос   _ Vос ■

Е ср     4У³ Ш    4( ^ °с )³

к                         2               ос

= 2 .

В результате получаем, что коэффициент неравномерности скоростей по сечению потока (коэффициент Кориолиса) для ламинарного потока

кор uлам    ^.

Для искомого турбулентного потока с эпюрой в виде прямоугольника (см. рис. 1, в)

кор

^ турб     , так как энергия суммы всех струек будет равна энергии для средней скорости потока.

Следует отметить, что αкор можно получить, поделив осевую скорость потока на среднюю, тогда:

• - для ламинарного потока с эпюрой в виде параболы

кор = -ос— = ?

^лам 0,5ъ ос 2 ;

- для турбулентного потока с эпюрой в виде усеченной параболы кор тУРб 0,85v ос 1,2;

- для потока с эпюрой скоростей в виде прямоугольника кор = ±_о турб    v ос

Приведенные выкладки свидетельствуют, что число Рейнольдса характеризует степень турбулентности потока только по скорости этого потока. Если же вносится в поток устройство, усредняющее скорости по сечению при том же числе Рейнольдса, то есть увеличивающее степень турбулизации потока, то необходим другой критерий. Им может служить коэффициент Кориолиса αкор, то есть коэффициент неравномерности распределения скоростей по сечению потока. При αкор = 2 – поток ламинарный с параболической формой эпюры скоростей, при αкор = 1 – поток максимальной или абсолютной турбулентности, когда эпюра скоростей имеет прямоугольную форму и разрушен подстилающий ламинарный слой у стенки трубы.

Коэффициент Кориолиса можно вычислить из уравнения Бернулли

АН = ко^ — + Z —,

2 д   ^ъ2 д'

где Н – напор, м;

• α^кор – коэффициент Кориолиса;

• v - скорость потока, м/с;

• д - ускорение свободного падения, м/с²;

• ζ – коэффициент местного сопротивления.

АН = ( а^кор + <) V | , ^ = _ар°Р + < , _а кор  ^- ^ .

Отсюда видно, что условие усреднения потока (увеличение коэффициента местного сопротивления ζ) должно быть больше, чем уменьшение квадрата скорости.

Выводы. Таким образом, приведенные выше исследования позволяют сделать вывод, что максимальный коэффициент теплоотдачи от греющего теплоносителя к стенке трубы можно получить либо значительным увеличением скорости, что в реальных условиях обеспечить затруднительно, либо введением в поток специального устройства – турбулизатора – с целью усреднения скоростей, а значит и температур, по сечению потока, то есть уменьшения коэффициента Кориолиса.