Теоретические основы формирования портфеля проектов АО "Аэропорт Архангельск"

Советом директоров АО «Аэропорт Архангельск» принята долгосрочная программа развития на период 2015-2025 гг. Программа содержит ряд мероприятий, часть которых может быть реализована как проекты. Обычно, при работе с проектами, для того чтобы лучше учесть общие ограничения, формируют портфель проектов. Возникает вопрос об эффективности и риске не проектов в отдельности, а всего портфеля.

В управлении финансами широко используют модель формирования эффективного портфеля ценных бумаг, предложенную Г. Марковицем в 1952 году. Суть модели в следующем: имеется возможность инвестирования денежных средств в приобретение ценных бумаг из ограниченного списка. Для каждой ценной бумаги с номером i на основании исторических данных известны её средняя доходность ц, стандартное отклонение доходности О[ и ковариация между всеми ценными бумагами рассматриваемого списка. Модель позволяет сформировать портфель ценных бумаг, обеспечивающий наименьшую дисперсию портфеля ор при доходности портфеля rp равной заданной доходности rq. При этом считают, что риск портфеля целиком определяется его дисперсией. Математически модель портфеля Марковица минимального риска можно выразить следующим образом:

{ а р = d^TVd ^ min

dTr = rq                                          (1)

dTe = 1

где а р - дисперсия портфеля;

d - вектор-столбец, содержащий доли ценных бумаг в портфеле;

V - ковариационная матрица,

Vu = covfarj), r - вектор-столбец, содержащий средние доходности ценных бумаг;

r_q - требуемая доходность портфеля;

e - единичный вектор-столбец, размерность которого равна количеству рассматриваемых ценных бумаг.

Элементы ковариационной матрицы показывают взаимозависимость изменения средней доходности двух различных компонентов портфеля. Отрицательная ковариация означает, что увеличению средней доходности одного компонента соответствует уменьшение средней доходности другого.

Понятно, что риск и доходность портфеля могут меняться только в диапазоне изменения риска и доходности входящих в него ценных бумаг, поэтому, на графике зависимости доходности портфеля от его риска все допустимые портфели окажутся внутри замкнутой области (Рисунок 1).

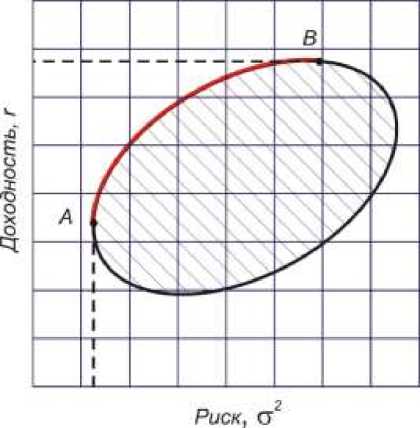
Рисунок 1 – Область допустимых портфелей

Соответственно, эффективные портфели, в зависимости от требуемой доходности, будут находиться на дуге A – B. В точке А портфель будет состоять из одной ценой бумаги с самой низкой дисперсией, а в точке B – с самой высокой доходностью.

Но модель Марковица в таком виде не подойдёт для составления эффективного портфеля проектов по двум причинам:

• 1)    для ценных бумаг имеется возможность на основе имеющейся исторической информации определить среднюю доходность, дисперсию и элементы ковариационной матрицы, для проектов такой возможности нет;

• 2)    в модели Марковица доли ценных бумаг в портфеле могут меняться непрерывно (с градацией, соответствующей стоимости одной акции), чего нельзя сказать про проекты. Проект может быть только принят или

• отклонён. Следовательно, решением должны стать не доли в портфеле, а бинарные значения (0, 1), где 0 соответствует отклонению проекта, а 1 – его включению в портфель.

В работе Двойченков П.Н. «Формирование портфеля проектов девелоперской компании на основе теории Г. Марковица» показаk возможность использования метода сценариев для определения средней доходности и её дисперсии для отдельного проекта. Доходностью проекта следует считать показатель IRR, так как он выражает относительную эффективность инвестиций и не зависит от ставки дисконтирования. Должны рассматриваться независимые проекты, отказ от одного из проектов не должен повлиять на возможность реализации любого из оставшихся. Если для реализации одного проекта требуются результаты другого, то их следует объединить в один проект.

Сначала следует выявить ключевые факторы, влияющие на доходность рассматриваемых проектов. Этот список факторов будет общим для всех проектов. Для каждого фактора выбирают ожидаемое, оптимистическое и пессимистическое значения и оценивают вероятность для каждого из этих значений. Сумма вероятностей должна быть равна единице. В результате при анализе проекта получают I исходов с номерами к = 1 ... Z, каждому из которых соответствует вероятность р_к и доходность IRR ^ . Например, выявлено два определяющих фактора: курс доллара и ставка по кредиту (в рублях). Прогнозы и вероятность значений приведены в таблице 1.

Таблица 1 – Ключевые факторы

Прогноз	Курс доллара		Ставка по кредиту
	Значение, руб.	Вероятность	Значение, %	Вероятность
Оптимистичный	60	0,1	15	0,1
Ожидаемый	62	0,6	20	0,6
Пессимистичный	70	0,3	25	0,3

В результате получим девять исходов с вероятностями, приведёнными в таблице 2.

Таблица 2 – Вероятности исходов

Номер к	1	2	3	4	5	6	7	8	9
Вероятность рк	0.03	0.18	0.09	0.06	0.36	0.18	0.01	0.06	0.03

Сумма вероятностей всех исходов будет равна единице

I

^Рк = -                             (2)

k=1

Как уже отмечалось, решением задачи должен быть вектор из нулей и единиц размерности п, где п - количество рассматриваемых проектов. Обозначим такой вектор х, а диагональную матрицу, диагональ которой составлена из элементов вектора х обозначим X. Для определения доходности портфеля проектов нам всё равно потребуются доли проектов в портфеле. Будем долей проекта в портфеле считать долю инвестиций в проект в общей сумме инвестиций в проекты, включённые в портфель. Обозначим вектор-столбец инвестиций в рассматриваемые проекты I. Сумму инвестиций в проекты, включенные в портфель, определим по формуле

SI = xT •I                                      (2)

где SI - сумма инвестиций в проекты, включенные в портфель.

Тогда вектор, содержащий доли каждого проекта в портфеле может быть определен по формуле

1             1

d = srX-I = —fX'1

где d - вектор долей проектов в портфеле.

Такой подход обеспечивает неотрицательные значения доли любого проекта в портфеле, а сумма долей всех проектов всегда будет равна единице.

Дисперсию портфеля можно выразить формулой

^ 2

= dT •V •d

^ххТ-т^-НххТ-тЧ

а его доходность формулой

Ip

= dT • г

^x-T^-¹) -^г

где г - вектор, содержащий IRR рассматриваемых проектов.

В отличии от портфеля ценных бумаг, вследствие дискретного включения проектов в портфель, мы не можем требовать равенства доходности портфеля проектов заданному значению. Может оказаться, что никакая из комбинаций проектов не в состоянии обеспечить заданную доходность. Для доходности портфеля проектов следует задавать ограничение не менее заданного значения гр >rq, где rq - заданное значение доходности. Таким образом, модель формирования эффективного портфеля проектов сводится к оптимизационной задаче нахождения вектора х, удовлетворяющего условию (6).

°i = (

.хт • I

•X^l) -У-(

.хт • I

• X • l) ^ min

/1      \ т

. (Хт-^'1) 'г>ъ

Для формирования эффективного портфеля проектов развития АО «Аэропорт Архангельск» следует:

• -    из программы развития выбрать мероприятия, которые можно

представить, как проекты;

• -    выявить самые значимые внешние факторы, влияющие на эффективность этих проектов, оценить границы и вероятность изменчивости этих факторов;

• -    определить среднее значение IRR каждого проекта, дисперсию и элементы ковариационной матрицы;

• -    решить задачу оптимизации.

Такой подход позволит не только сформировать портфель с максимальной средней доходностью, но и значительно сократить риск портфеля, выражаемый его дисперсией.