Теоретические основы исследования процессов деформации заготовки без изменения формы и размеров

Одной из характерных особенностей современного металлургического производства является тенденция к ужесточению требований к качеству готовой продукции и повышению ее эксплуатационной надежности и долговечности. Актуальными направлениями развития металлургического производства являются:

• -    получение сталей и сплавов заданного химического состава, макро- и микроструктуры, уровня механических свойств и долговечности изделий в определенных условиях эксплуатации;

• -    получение изделий требуемой формы, ассортимента, точности размеров и чистоты поверхности;

• -    минимизация производственных затрат при удовлетворении ограничительных требований к качеству продукции, указанных в нормативнотехнической документации;

Важной задачей является разработка и освоение новых технологических процессов обработки давлением, сочетающих незначительное изменение формы и размеров заготовки с интенсивной проработкой структуры при деформации. Этим требованиям отвечает процесс равноканального углового прессования (РКУП). Процесс РКУП довольно широко описан в литературе [1–11], однако в связи с поставленной задачей выявлены новые направления исследования процесса равноканального углового прессования, связанные с достижением максимального упрочнения металла, измельчением зерна, а также изучением процесса разрушения металла.

Механика напряженно-деформированного состояния и разрушения металла при РКУП Напряженное состояние в общем случае описывается следующими уравнениями:

I a ]Л = a + 4ctg I y + PI;

I a 1CT AO = т s ctg I 2 + e 1+ CT 2;

Io I a 1                  1ct = ct AOB = т s I 2ctg I - + P I + 2a-2ф1 +

. I a I

• + ФтsctgI - + P I + CT2;

  ^CT 1 = ^т s

  
  

  + в I + 2 a — 2 ф I +

  
  

  ⁺² ф^т s

  
  

. Ia 1 h ctg I - + P | + -

1 2 J a

+ ст ₂

В приведенных выражениях коэффициент трения ф (трение учитывается по методу Зибеля т k = фт _s ) выражается через углы a и в :

• a    = |аrccos( ф ) — 2р|

т при ф = —- > cos2e [1]. Т s

Для оценки поврежденности металла при РКУП воспользуемся моделью накопления повре-жденности металла при монотонной деформации по методике [12]:

ность Л p , от термомеханических параметров процесса у , ц_а , Н , 6 ); -^ - показатель напряженного состояния; х , X , b , а₀ - коэффициенты, зависящие от марки стали или сплава (их находят, используя опытные данные, по методу наименьших квадратов) [12].

Условия деформирования металла при РКУП

Для большинства процессов высокотемпературной обработки металлов давлением характерным является равновесный процесс деформации. С точки зрения феноменологической теории на основе высказанной Ю.М. Вайнблатом гипотезы о том, что при достижении некоторой критической деформации процесс становится равновесным. В таком случае решающее значение на эволюцию зеренной структуры, а, следовательно, и на механические и технологические свойства оказывают температурно-скоростные условия деформации, а не степень деформации. Простое соотношение, связывающее температуру и скорость деформации, можно получить, введя время разупрочнения t как параметр, влияющий на сопротивление деформации при горячей обработке:

Л 1

®= J

а Л ^{а — 1}

a

p

d X ,

I a 1

где Лp = х exp I X — I - степень деформации сдви га, накопленная материальной частицей металла от момента возникновения пластической деформации до момента появления макротрещины (описывается аппроксимированной формулой из диаграммы

1+ь - пластичности; а = а0 T - коэффициент, характеризующий интенсивность накопления поврежден-ности материала (он зависит, также как и пластич-

d ^a s dt

dt d £и

k

^ и exp

Q

R 6

Для процесса горячей обработки металла давлением уравнение состояния, связывающее сопротивление деформации в установившей стадии ст _s , скорость деформации ^ _и и температуру 6 , можно

представить выражением

^ и =^Л 1 ^exP ( Р^ст s ) • ^exP

Q

—

R 6

[13, 14].

Таким образом, задача обеспечения максимального упрочнения в условиях равновесности

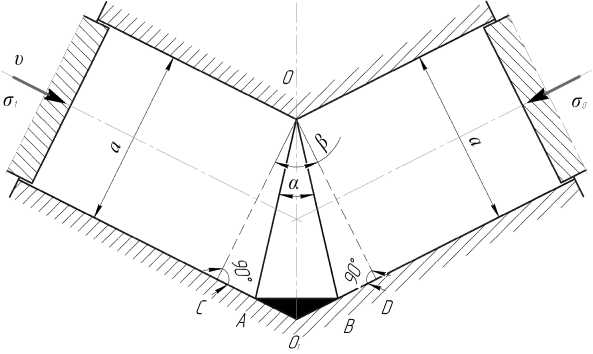
Рис. 1. Схема равноканального углового прессования: AOB – геометрический очаг деформации, зона пластического течения; АО 1 В – застойная зона

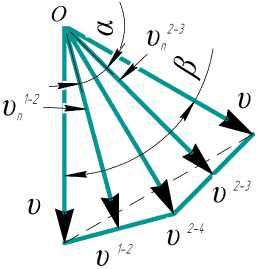
Рис. 2. Годограф скоростей: υ _n ^1–2 , υ _n ^2–3 – нормальные составляющие скоростей течения металла; υ ^1–2 , υ ^2–3 , υ ^2–4 – касательные составляющие скоростей течения металла, скорости среза

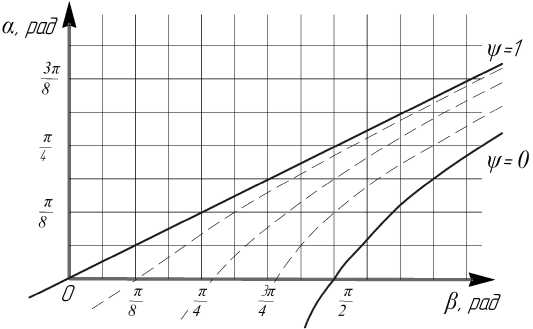
Рис. 3. Зависимость угла α от угла поворота каналов β : α – угол, описывающий пластическую область; β – угол поворота каналов, ψ – коэффициент трения по Зибелю

процесса РКУП сводится к выбору необходимой температуры предварительного нагрева заготовки и увеличения скорости деформации ^ _и ^ х , это условие может быть достигнуто лишь в случае, когда а ^ 0 (рис. 1), то есть размер пластической области должен быть минимальным.

Для определения оптимальных условий деформирования при РКУП воспользуемся методом верхней оценкис использованием кинематических моделей очага деформации из жестких блоков. Использование принципа виртуальных скоростей позволило построить годограф скоростей, из анализа которого (рис. 2) был составлен функционал принципа возможных изменений деформированного состояния, вычислена первая производная функционала по варьируемому па-

раметру а :

I = jT5 •HdV-j p,

V

Здесь j x ₅ • HdV

V

S

–

dI

)i • v i dS и---- = 0 . d а

мощность внутренних сил

(мощность деформации); j p_t • v i dS

–

мощность

S внешних воздействий на исследуемый материал.

Результатом упрощения уравнения стала зависимость угла а от угла поворота каналов в при различных коэффициентах трения у (рис. 3):

^ + 1        2

2 fP а)     2 а cos2   - cos —

( 2 2 J 2

.

Из условия минимизации угла а результатом выбора оптимальных режимов деформирования является:

• 1)    выбор конфигурации каналов при равноканальном угловом прессовании (угол поворота каналов р );

• 2)    при соответствующей конфигурации кана-

лов подбор необходимой смазки для обеспечения необходимого коэффициента трения у ;

3) при а ^ 0 , у = cos р .

Выбор рациональных режимов деформирования при РКУП с учетом упрочнения и поврежденности металла

Для учета упрочнения воспользуемся формулой »5 =^ 5 0 + д Л b, где g и b – экспериментальные коэффициенты соответствующего материала (стали или сплава) [15]; зависимость Р(у) при условии а ^ 0 для различных материалов показана на рис. 4.

Пользуясь графиком (см. рис. 4) для определенного материала, можно осуществить выбор оптимального режима деформирования при соответствующем коэффициенте трения.

Важно заметить, что для процесса получения ультрадисперсной микроструктуры и, как следствие, высоких механических и эксплуатационных свойств металла после РКУП, недопустимо даже микроразрушение ( ю « 0,25 ), не говоря уже о макроразрушении ( ю = 1) [12]. При ю < ю * = 0,25 достигаются условия недопустимости появления микродефектов. По результатам выбора оптимальных режимов деформации при условии а ^ 0 осуществим проверку по поврежденности металла. На рис. 5 графически приведена зависимость повреж-денности металла ю от угла поворота каналов P при соответствующих оптимальным режимам деформации коэффициентах трения у (см. рис. 4).

Результат наглядно показывает, что при оптимальных режимах деформации РКУП стали (сплава) поврежденность ю находится в пределах допустимых значений ( ю< 0,25). Таким образом, представленные режимы деформации при РКУП позволяют осуществлять процесс пластической деформации для выбранных материалов без разрушения.

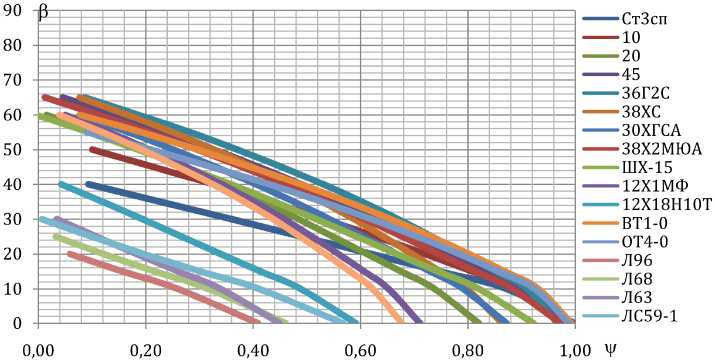
Рис. 4. Зависимость угла поворота каналов β от коэффициента трения ψ для различных материалов

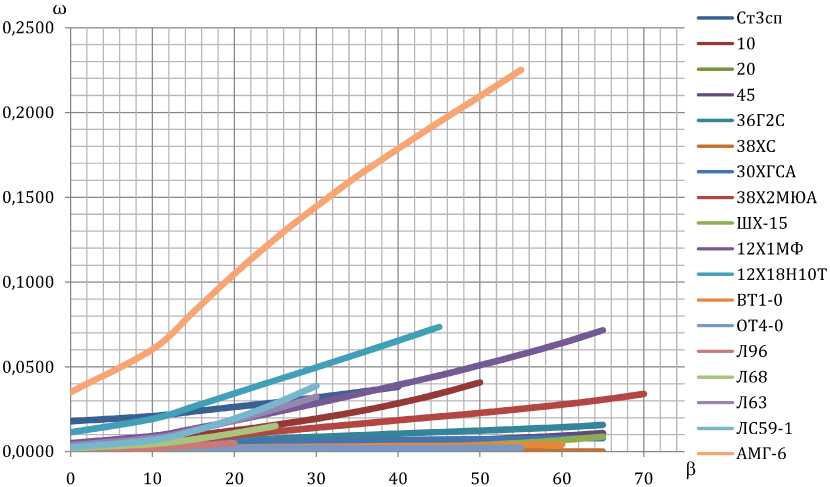
Рис. 5. Зависимость поврежденности металла ω от угла поворота каналов β

Компьютерное моделирование процесса РКУП металла

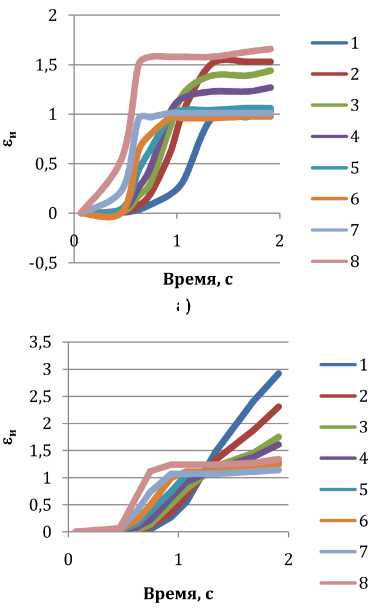
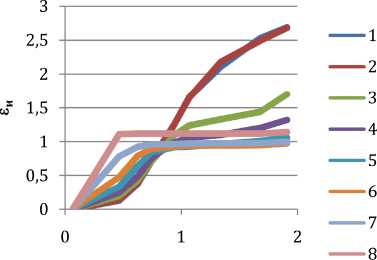
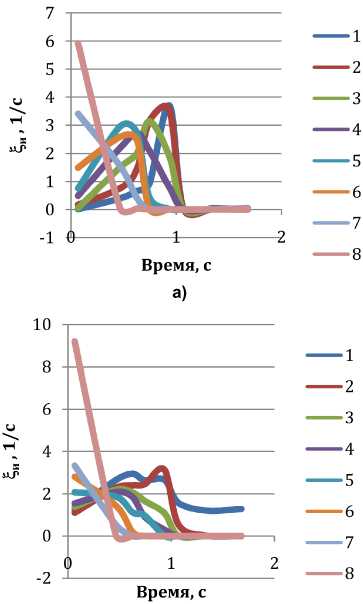
В ходе исследования результатов эксперимента были получены данные о деформированном состоянии металла. В качестве исследуемых параметров, характеризующих деформированное состояние металла в очаге деформации (точки 1–8), были выбраны скорость деформации ξ _и (рис. 7) и степень деформации ε _и (рис. 6) при различных условиях трения.

Характер зависимости степени деформации εи от времени таков, что в очаге деформации (τ = 0,5–1 с) наблюдается резкий рост степени деформации εи до 1 при малых показателях трения (ψ < 0,05) и 1,5 при повышенных. В дальнейшем степень деформации εи центральной части метал- ла (точки 3–6) практически не изменяется, рост степени деформации εи наблюдается в прикон-тактных зонах (точки 1, 2, 7, 8) ввиду влияния трения. Процесс накопления степени деформации εи при РКУП идет тем быстрее, чем меньше показатель трения ψ. Количественно степень деформации εи при различных условиях трения лежит в пределах от 2 до 3.

Анализ скорости деформации ξ _и процесса РКУП при различных показателях трения ψ показывает, что с увеличением показателя трения ψ процесс деформирования длится дольше, сохраняя при этом соответствующие значения скорости деформации. При ψ = 0 деформация проходит практически мгновенно (ярко выраженные экстремумы на рис. 7, а).

а)

в)

Время, с

б)

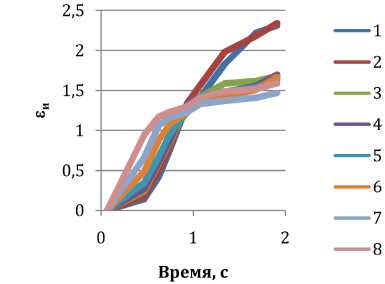
Рис. 6. Изменение ε _и вдоль траектории течения частиц металла в очаге деформации: а – без трения; б – ψ = 0,05; в – ψ = 0,15; г – ψ = 0,3

в)

г)

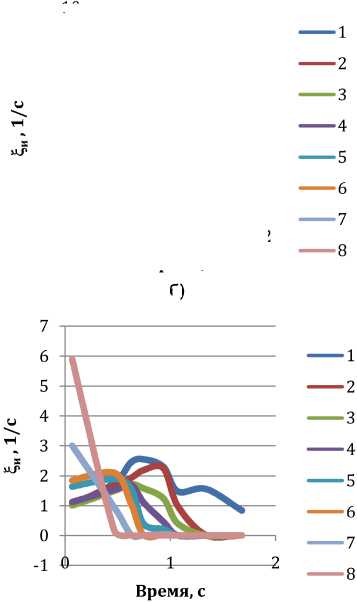
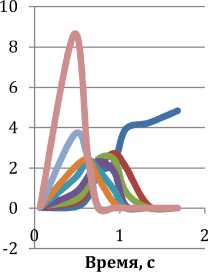
Рис. 7. Изменение ξ _и вдоль траектории течения частиц металла в очаге деформации: а – без трения; б – ψ = 0,05; в – ψ = 0,15; г – ψ = 0,3

б)

Наибольшие значения скорости деформации ξ _и возникают в областях вблизи поворота каналов (точка 8, рис. 8).

Представленные результаты показывают, что с увеличением показателя трения ψ величина за- стойной области увеличивается. Это не противоречит теоретическому решению, а подтверждает его.

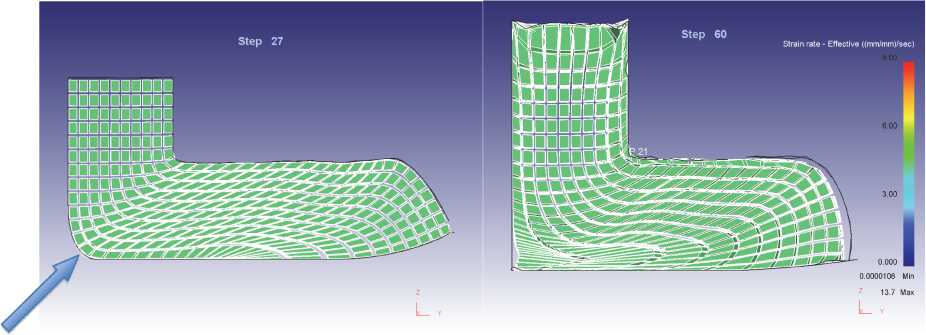
Анализ лагранжевой сетки (рис. 10) и характер изменения скорости деформации (рис. 9) по ширине очага деформации (точки 1–21) подтвер-

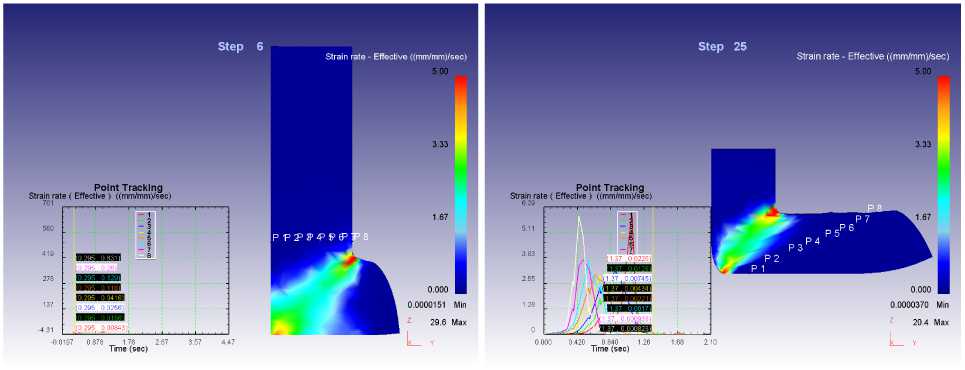
Рис. 8. Изменение скорости деформации ξ _и вдоль траектории течения частиц металла в очаге деформации при ψ = 0

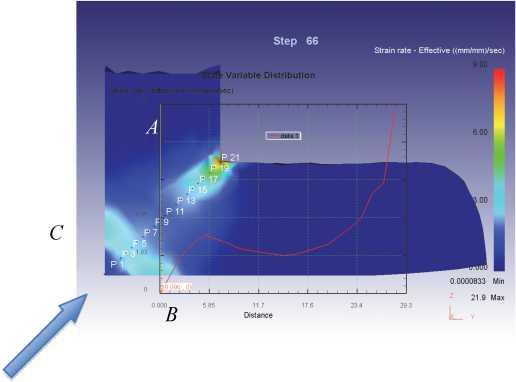
Рис. 9. Изменение ξ _и металла по ширине очага деформации при ψ = 0,3: АВС – зона пластического течения

а)                                                               б)

Рис. 10. Лагранжева сетка при РКУП: а – ψ = 0; б – ψ = 0,3

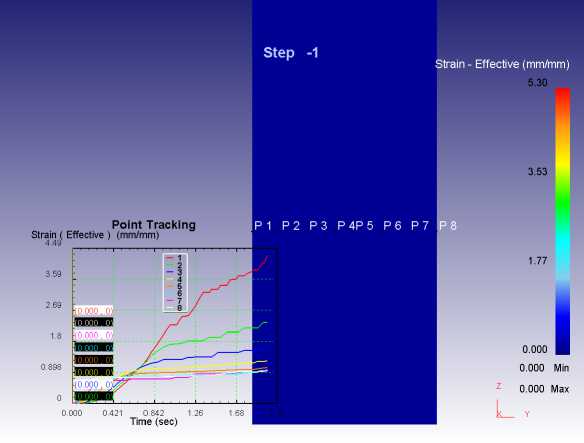
Рис. 11. Выбор точек, для которых производился расчет степени деформации сдвига

ждают наличие застойной зоны на повороте каналов, где металл практически не деформируется ( ^ _и ^ 0), а вся деформация сосредоточена в пределах «веера» АВС .

Анализ неоднородности деформации при РКУП

Результаты расчетов размеров очага деформации, степени деформации для восьми частиц, имеющих различную координату по сечению заго-

пряжений трения градиент скорости частиц меньше, чем для центральной области очага деформации. Для оценки неравномерности деформации по сечению заготовки выполнен расчет накопленной степени деформации сдвига частицами по восьми траекториям для различных условий трения (рис. 11).

Среднее значение степени деформации по высоте

° иср

n

=1 Z6

n 1 = 1

и i ,

товки сравним с аналогичными характеристиками, полученными по теоретическим формулам. Степень деформации подсчитали по формуле

£

и

Λ

, 3

где

Л = а + 4ctg

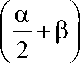
а = |arccos( у ) - 2р|, у -

где i - номер траектории частицы, n = 8. Неравномерность деформации по высоте очага деформации можно оценить с помощью коэффициента вариации

S - 100%

V                      ,

^£ иср

n

показатель трения по Зибелю, в - угол поворота каналов при РКУП.

В застойной области под воздействием на-

n гдеS=[n—i g (

ε

и i

—

² иср

1/2

- среднеквадра-

тичное отклонение. Результаты расчетов представлены в таблице, а также на рис. 12, 13.

Результаты компьютерного моделирования

№ траектории	Степень деформации сдвига ( £ и i )
	При у = 0	При у = 0,05	При у = 0,15	При у = 0,3
1	4,157	4,396	4,659	5,006
2	2,615	2,944	3,274	3,377
3	1,940	2,061	2,234	2,286
4	1,573	1,621	1,639	1,743
5	1,483	1,385	1,458	1,662
6	1,346	1,171	1,263	1,533
7	1,247	1,091	1,174	1,238
8	1,305	1,271	1,036	1,204
Статистические характеристики результатов
£ иср	1,958	1,993	2,092	2,256
S	0,996	1,147	1,268	1,315
V = S - 100%/ £ иср	50,9	57,6	60,6	58,3
£ и теор	2	2,226	2,072	1,87

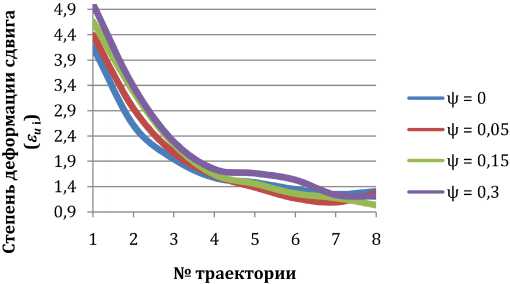
Рис. 12. Распределение степени деформации по траекториям

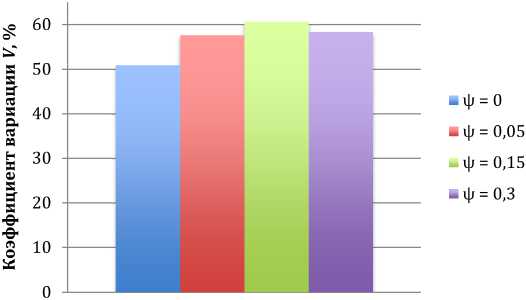
Рис. 13. Коэффициент вариации V для различных условий трения

По графикам (см. рис. 12, 13) видно, что степень деформации ε_{и i} в 4–5 раз больше в застойной области по сравнению с остальной частью очага деформации. Кроме того, с увеличением показателя трения ψ значения степени деформации ε_{и i} увеличиваются соответственно. Такой характер распределения неоднородности деформации подтверждается теорией. Коэффициент вариации V для различных условий трения лежит в пределах от 50–60 %, что свидетельствует о значительной неоднородности деформации по длине очага деформации. Формирование «веера» деформации при увеличении показателя трения ψ от 0 до 0,3 подтверждает теоретические расчеты.

Заключение

В работе приведено теоретическое исследование механики деформированного состояния и разрушения металла при РКУП методами линий скольжения и верхней оценки, а также математическое моделирование в программном комплексе Deform-3D. Вычислительный эксперимент с достаточной точностью подтверждает теоретические исследования РКУП. Условие минимизации застойной области (то есть снижение угла α → 0 ) является важной особенностью реализации оптимальных режимов деформирования при РКУП для различных условий трения, при котором достига- ется максимальное упрочнение металла без разрушения. Задача обеспечения максимального упрочнения, а, следовательно, и измельчения зерна, в условиях равновесности процесса РКУП сводится к выбору необходимой температуры предварительного нагрева заготовки и увеличения скорости деформации ξи → ∞ , которое достигается в случае, когда α → 0 , то есть размер пластической области должен быть минимальным.