Теоретические основы комплексных измерений показателей качества нефтепродуктов методом ядерного магнитного резонанса

Малышева-Стройкова Александра Николаевна, аспирант кафедры «Электротехника».

кислоты, ароматических углеводородов, бензола, детонационная стойкость (октановое и цетановое числа), плотность, вязкость, температура вспышки, давление насыщенных паров, точка росы и многие другие специфические показатели, характерные для отдельных видов углеводородных соединений. Точность определения химического состава и его структуры сопоставима с данными рентгеноструктурного анализа. Число и положение линий в спектрах ЯМР однозначно характеризуют все фракции сырой нефти и углеводородных топлив. Однако определение показателей качества нефтепродуктов через выявление химического состава можно признать фундаментальным, но с точки зрения оперативности нельзя назвать перспективным. Обработка спектрометрических данных требует времени и для каждого показателя качества специальных подходов и алгоритмов, которые в большинстве своем еще не разработаны. Не исследованы вопросы взаимосвязи показателей качества нефтепродуктов с характеристиками ЯМР - спектров. Не решены вопросы математического моделирования процесса комплексного измерения показателей качества углеводородных топлив, нет алгоритмов и программ обработки экспериментальных данных с позиций получения функции преобразования измерительных приборов, работающих в реальном времени (на потоке). В статье излагаются теоретических основы комплек- сных измерений показателей качества нефтепродуктов на основе ЯМР, которые следует рассматривать как небольшой шаг, направленный на устранение указанного пробела в теории и практике ЯМР-исследований нефтепродуктов. Исследуются основные возможности метода ЯМР для определения показателей качества нефтепродуктов и рассматриваются математические модели процедуры измерений при различных методах получения и обработки информации. Для наблюдения ядерного магнитного резонанса необходимо поместить образец в сильное однородное магнитное поле Но (рис/ 1) и подействовать на него излучением с частотой V, удовлетворяющей уравнению

— V        -Н.

2л 0 ’

которое является основным уравнением ядерно-го магнитного резонанса.

Здесь у - гиромагнитное отношение, характеризующее данный вид ядер [1-5].

Магнит вызывает расщепление энергетических уровней магнитных ядер, т.е. создает необходимые условия для поглощения радиочастотного излучения. Радиочастотный генератор возбуждает магнитное поле, перпендикулярное к постоянному полю. При определенном соотношении этих полей наступает резонансное поглощение энергии, которое регистрируется радиочастотным детектором.

Условия резонанса можно достичь либо изменением напряженности постоянного магнитного поля, либо изменением частоты генератора. Чаще используется второй принцип. В настоящее время наиболее широко применяются спектрометры протонного магнитного резонанса с частотой 60 и 100 Мгц (в последние годы стали изготавливаться приборы с частотой 220

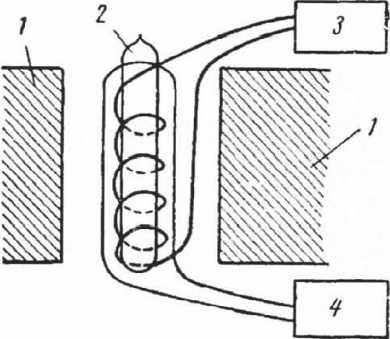
Рис. 1. Схема спектрометра ЯМР:

1 — магнит; 2—ампула с образцом;

3 — детектор; 4 — генератор радиочастоты

Мгц). Подробно теория и аппаратурная реализация ЯМР- спектрометрии изложена в [1-5].

Основные признаки измерительного процесса показателей качества топлив на основе ЯМР состоят в следующем:

• 1.    Измерение производится путем определения молекулярного и структурного состава вещества. Изменение химического состава топлива вещества приводит к изменению показателей качества.

• 2.    Измерение основано на определении частоты поглощения радиочастотного излучения исследуемым веществом, которая фиксируется в единицах химического сдвига относительно эталонного вещества.

• 3.    Кроме химического сдвига информация о количественном содержании химических элементов содержится в амплитуде (интенсивности) сигнала (ЯМР) на частоте химического сдвига.

• 4.    Эталонное вещество вводится в виде присадки в контролируемую среду, либо хранится непосредственно в датчике, в конструкции которого заложена такая возможность.

• 5.    ЯМР-характеристики эталонного продукта могут храниться в ЭВМ измерительной системы, но это хуже, так как они плавают в зависимости от внешних условий, например температуры, напряжения питания, старения элементов, напряженности магнитного поля.

Все перечисленные признаки необходимо использовать для создания общей теории измерений показателей качества на основе ЯМР.

Пусть имеется нефтепродукт, у которого нужно определить перечисленную выше совокупность ^ Q i } показателей качества методами ЯМР, то есть на основе определения химического сдвига относительно эталона (эталонов) с известными значениями исследуемых параметров. При этом каждый показатель качества изменяется в диапазоне [ Q , _>min - Q , _max ^] . При построении измерительной процедуры, связанной с определением неизвестных показателей качества возможны два подхода.

• 1.    Эталонное вещество одно для всех показателей качества. При этом предполагается, что у эталонного вещества известны все вышеперечисленные показатели качества.

• 2.    Под каждый показатель качества индивидуально подбирается эталонное вещество, известные ЯМР-характеристики которого используются в измерительной процедуре при вычислении конкретного показателя качества.

Каждый из этих подходов имеет достоинства и недостатки, которые будут анализироваться в процессе развития теории ЯМР-измерений показателей качества нефтепродуктов. При первом подходе имеем один эталонный продукт под все показатели качества. Здесь всем показателям качества Qk эталонного продукта (k=1…n) соответствует химический сдвиг q =0. При изменении показателя качества Qk исследуемого продукта в какую-либо сторону от эталонного значения возникает химический сдвиг qk . При этом изменение каждого показателя качества Qk продукта даст свой химический сдвиг. Например, изменение октанового числа бензина, которое условно назовем показателем Qk , при постоянных других показателях качества (вязкости, плотности, содержание серы и т.д. ) даст смещение qk . Изменение содержания серы, которое условно назовем Qk+1 , при постоянных других показателях качества даст смещение qk+1 . Ясно, что все показатели качества взаимосвязаны, то есть изменение октанового числа или содержания серы приведет к изменению плотности и вязкости и т. д. Поэтому рассмотренная выше ситуация является гипотетической. Однако математическая постановка вполне допустима, так как задача математики будет состоять в оценке влияния каждого показателя качества на суммарный химический сдвиг. В общем случае суммарный химический сдвиг, вызванный изменением показателей качества нефтепродукта от эталонного значения, может описываться функцией:

q = F (Q1, Q 2,... Qk... Qn) . (2)

Функция (2) неизвестна. Ее поиск является важнейшей задачей математического описания измерительной процедуры. Учитывая, что любой измерительный процесс подразумевает в себе, кроме сбора и обработки информации, также операцию калибровки прибора по известным эталонным параметрам, для решения поставленной задачи предложен алгоритм измерений, сущность которого состоит в том, что при неизвестной функции F составляется калибровочная модель процесса измерения. Для этого берется несколько образцов топлива с известными значениями показателей качества, определенными лабораторными способами и ставится им в соответствие столько же отсчетов химических сдвигов. При этом необходимо, чтобы образцовые топлива полностью перекрывали ожидаемый диапазон изменений определяемых показателей качества. Количество образцовых топлив N должно быть не меньше числа определяемых показателей качества n (N > n) . Пусть имеется N калибровочных образцов топлива. Каждый из этих образцов имеет свой набор показателей качества. Например, первый образец (N = 1) имеет набор показателей качества Q_1,1 , Q_1,2 ,…Q_1,k , … Q_1,n . Образец N = i имеет набор показателей качества Q_i,1 , Q_i,2 ,…Q_i,k , … Q_i,n . Образец ( N = N) имеет набор показателей качес ^, тва Q_N,1 , Q_N,2 ,…Q_N,k , … Q_N,n

Здесь первый индекс соответствует номеру калибровочного образца, второй индекс – номеру показателя качества. При построении калибровочной модели для произвольных значений измеряемых параметров всегда можно подобрать такие нормирующие коэффициенты b_k , что будут выполняться равенства:

n

(q = bQ +.„+ b Q . +.„+ bQ n = ^b Q n к=1

n q = bQi +... +bkQ, +..+ bQ, n = ^bQ, k=1

n qn = bQ;J +.-+bkQ,t +...+b,e,„ = 5bQ„, k=1

n

I    S n = bQ N ,1 +~ + b „ Q N, + ... + b n Q Nn = ^^Q„

^V                                               k = 1

В системе уравнений (3) q_i – химический сдвиг, соответствующий i – му калибровочному образцу топлива.

Система имеет N уравнений для n неизвестных b 1 ... b n . Учитывая, что N > n из системы (3) всегда можно выбрать n уравнений, достаточных для нахождения неизвестных коэффициентов b_k . Необходимо выбирать наиболее информативные уравнения, охватывающие наибольшие диапазоны химических сдвигов и определяемых показателей качества. В частном случае достаточно n верхних уравнений из системы (3), которые для упрощения записи предполагается использовать в дальнейших математических выкладках. Из системы (3) находится совокупность коэффициентов b_k , которые в средневзвешенной форме аналитически определяют взаимосвязь химического сдвига с набором показателей качества исследуемого топлива:

n qX = b1 QX, 1 + ... + bkQXk + ... + bnQxnn = ^bkQXk (4) k =1

где QX,k – искомое значение показателя качества контролируемого топлива, qX – измеренный химический сдвиг контролируемого топлива.

При этом коэффициенты b_k определяются по формуле:

b =^bk k ^ , где

^Q 1,1 ... ^Q 1, k ... ^Q 1, n

a = Q,,...Q,....Q,„ i,1           i,k           i, n

^Q n ,1

.. ^Q n , k

^Q n , n

^Q 1,1 ... ^q 1, k ... ^Q 1, n

A b k

^Q n ,1

.. q _{n , k}

^Q n , n

Выражения (3) ... (5) составляют в общем виде математическую модель измерительного процесса определения показателей качества по калибровочной модели, где (4) определяет вклад каждого показателя качества в суммарный химический сдвиг испытуемого топлива. Однако оно не определяет каждый показатель качества. Для определения каждого показателя качества через химический сдвиг необходимы дополнительные исследования, позволяющие составить уравнения, связывающие искомые параметры с характеристиками ядерного магнитного резонанса для конкретного топлива. Из (4) следует, что для оцениваемого топлива каждому химическому сдвигу соответствует определенный набор показателей качества. Справедливо также то, что закон изменения химического сдвига от каждого показателя качества индивидуален.

Показатели качества Q_k имеют разную размерность, поэтому изображение их на одном гра-

фике невозможно. Однако, если показатели качества брать нормированными, определяемыми как текущее значение, деленное на максимальное значение, то иллюстрирование становится возможным в относительных (безразмерных) единицах. Например, если показатель качества Q_k имеет диапазон изменения [Q_{k min} ч Q_{k, max} ], то нормированный показатель качества определится по формуле

^Q N k = ^Q' . (6)

k ,max

Тогда, для нормированных показателей качества любое нефтепродукт может характеризоваться набором функций (графиков), показанных на рис. 2 , связывающих показатели качества с химическим сдвигом.

Таким образом, по набору экспериментальных данных для каждого показателя качества можно методами математической регрессии составить аналитическую зависимость, связывающую показатель качества с химическим сдвигом.

QN1 = fx(q ), QN2 = f2(q )...

QNt = ft(q )■•• QNn = f,(q ). (7)

Набор нормированных показателей качества для произвольного значения химического сдвига q_X определится по формуле

QNk,x = fk (qx ).        (8)

Абсолютное значение показателя качества определится по формуле

^Qk , X = QN k , X • ^Qk ,max = ^Qk ,max ’ ^fk ⁽ q x ) = ^Fk ⁽ q x ) .(9)

Аппроксимацию экспериментальных точек можно проводить стандартными программами математического пакета МАТСАD по методу

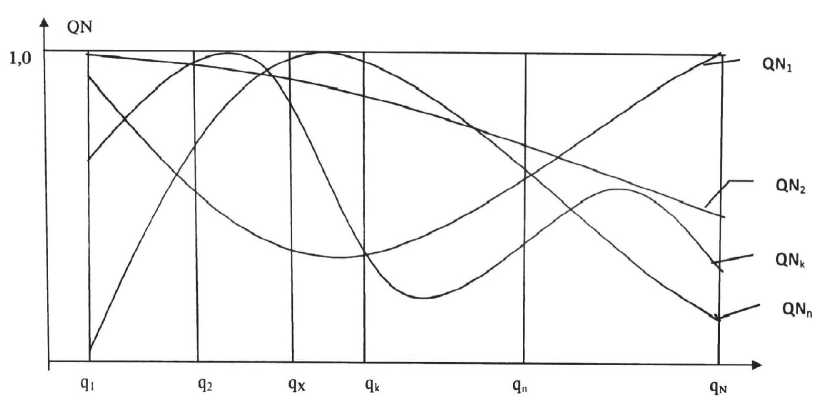
Рис. 2. Иллюстрация к методике определения показателей качества по суммарному химическому сдвигу для разных наборов показателей качества

наименьших квадратов различными функциями заданного вида, в простейшем случае степенным полиномом [10].

Формула (9) легко применима, если определяется один показатель качества Q_k , например плотность, или октановое число. В этом случае система уравнений (3) примет вид

Q i = b k Q i , k . (io)

Тогда b _k = q i I Q i _k , и выражение (4) примет вид

Q x = b k^Qx , k , ^qx , k = Q x I bk . (ii)

Выражения (11) напрямую определяют показатель качества Q_k через химический сдвиг при калибровке по i-тому образцовому топливу и справедливо, если химический сдвиг линейно зависит от показателя качества по формуле (10). Это имеет место быть тогда, когда изменения показателя качества происходит в окрестности калибровочного образца. В широком диапазоне изменений химический сдвиг и показатель качества нелинейно зависят друг от друга и выражения (11) будут иметь вид (9), откуда следует:

qx = Ft4 Qx,) ■ (12)

Поиск функции (12), можно проводить не только на основе набора характеристик, показанных на рис. 3 по методике, описываемой выражениями (6) – (9), но и по следующей схеме. Можно взять N +1 калибровочных топлив с известными значениями k – го показателя качества Q_i,k (i=0,1,2,…N) и соответствующие им химические сдвиги q_i . При этом значения других показателей качества во внимание не принимать. Очевидно, что можно составить систему уравнений для поиска функции (9) в виде полинома.

<   Qi, k Fk (qi) b0 + bl q + b2qi +— + bjqi +—+ bq (13)

Решение этой системы уравнений относительно коэффициентов bj определяется выражением bj

A b j

A

(14),

в котором:

1 q 0 q 0 ... Q 0, _k ... q 0

^A b j = ¹ Qi g.-Q i,k ■■■ q N

• 1    q_Nq_N ... Q_N , _k ... q_N

Тогда уравнение, связывающее искомый показатель качества исследуемого топлива с рассматриваемым электрофизическим параметром определится:

Qx,k = Fk (Qx ) = b0 + b 1 Qx + b2qX

n

• + b j q x + ■■■ + ^bN^qx ^— ^ b j q x . (15) j - 0

Выражение (15) отличается от (9) способом получения. Для получения (9) использовалось одно калибровочное топливо, и в процедуре поиска использовались все показатели качества. Для получения (15) использовались N+1 эталонных топлив, в которых для поиска использовался только один показатель качества. Точность математического моделирования функции преобразования (15) зависит от числа эталонных топлив и возрастает с их увеличением. Реально сигнал ЯМР является более информативным. Кроме частоты резонанса информацию о показателях качества несет в себе интенсивность (относительная амплитуда сигнала). Идеология метода состоит в том, что снимается несколько спектральных характеристик топлива с заранее известными значениями исследуемого показателя качества Q_1k, …Q_i,k … Q_N,k в заявленном диапазоне измерений (рис 3). Здесь индекс i соответствует номеру образцового топлива, k – номеру показателя качества, N – число образцовых топлив с известными значениями показателя качества.

Если взять N дискретных отсчетов в каждой спектрометрической характеристике, то при построении калибровочной модели можно подобрать такие нормирующие коэффициенты b_i , что будут выполняться равенства:

p

Q i , k = ^b i « i ⁽ Q i ) + ■■■ + b a ⁽ q ) + ■■■ + b_N a ⁽ Q n ) = ^ b a ⁽q_t) (16)

i = 1

A =

1 q 0 q 0 ... q 0 ... q 0

,

Решая эту систему можно найти такую совокупность коэффициентов b_k , которые в средневзвешенной форме будут определять контролируемый показатель качества Q_X,k в исследуемом топливе:                          _N

Q xk = b i ^ x ⁽q₁^{) +} ... ⁺ bi « x ⁽q i ^{) + ... +} Vx ⁽ Qn ) ^b ^b x ^{( q (} q ) ,⁽¹⁷⁾

i = 1

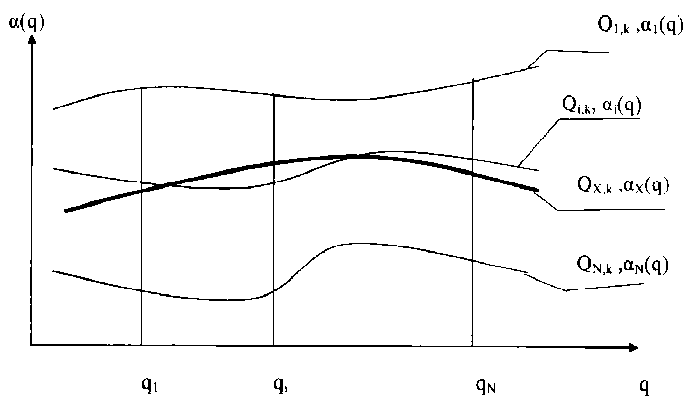
Рис. 3. Иллюстрация к методике определения показателя качества по спектрометрическим характеристикам:

Q₁, Q_i, …Q_P – значения показателя качества в калибровочных образцах топлива, p – число калибровочных образцов, Q_X – спектр исследуемого топлива с неизвестным значением показателя качества

« X ( q i ) — совокупность дискретных отсчетов ЯМР-спектра контролируемого топлива. При этом коэффициенты b_k определяются по формуле

,             (18)

в которой:

« i q !... « ( q₁').. « _x⁽ q N )

^A = « , .( q i )... « , ⁽ q_i)- a _i⁽ q N )

« N ⁽ q i )." « N ⁽ q i \-«N ⁽ q N )

A b i =	a i ( q i) ... Qu t ... a i ( q N )
	a ( qiY.Q k ... « . ( q N )
	aN ( q i) ..Q N,t ... « N ( q N )

.

Система (16) имеет единственное решение, если главный определитель отличен от нуля. Можно выбрать такие значения отсчетов спектральной характеристики, которые исключают равенство нулю главного определителя.

Частный случай определения значения показателя качества по двум калибровочным топли- вам, полностью перекрывающим диапазон ожидаемых значений Qmin,k ... Qmax,k , Q1 = Qmin,k , Q2= Qmax,k. Тогда выражение (17) примет вид:

Qx,k = b«x (q,) + bi«x(q2) ,    (20)

b _     « i ⁽ q 2 ) Q 2 « 2 ^{( q} 2 ) Q 1

^{1 a} i⁽ q , ^{) a} 2⁽ q 2 ) - ^a i ⁽ q 2^{) a} 2⁽ q , )

^b 2 =

^a 2⁽ q i ) ^Q 1 ^a i⁽ q i ) ^Q 2

^a i⁽ q i^{) a} 2⁽ q 2 ) ^{- a} i⁽ q 2^{) a} 2⁽ q i ) ^.

Численный эксперимент показывает, что при любых значениях 0 искомое значение находится в интервале Q_minx< Q_max , что также распространяется на множество дискретных отсчетов и полностью подтверждает выводы, сделанные выше выводы по отношению к химическим сдвигам q_,i . Это определяет возможность использования отсчетов спектрометрической характеристики для определения показателей качества с построением калибровочной модели. Математическая модель (17) позволяет построить процедуру измерения для любого показателя качества. Необходимо только иметь набор эталонных топлив с известными показателями качества Q_i.k, который присутствует в определителе (19). Разработанная математическая модель процедуры измерения, позволяет находить функцию преобразования прибора по каждому показателю качества при различных исходных данных, связанных с наличием образцовых топлив. Предложенная методика измерений не требует точного знания функции, связывающей искомый показатель качества с отсчетами ЯМР-характе-ристики исследуемого образца параметрами. Она предполагает создание математической модели на основе эталонных образцов топлив с известными значениями показателей качества.