Теоретические основы моделирования динамических характеристик приводов перспективных космических аппаратов с учетом функционирования осцилляторов

УДК 62-83                                                 

Введение. На современном этапе развития авиакосмической отрасли сохраняют актуальность практические задачи обеспечения динамической точности угловых и линейных перемещений прецизионных элементов конструкции (ПЭК) и целевой аппаратуры (ЦА) перспективных космических аппаратов (КА) при действии внутренних источников возмущений. Такими источниками считаются устройства, приборы и приводы космического аппарата и научной аппаратуры. Движущиеся и вращающиеся массы указанного оборудования в режимах прецизионного наведения формируют вибрационные возмущения [1, 2]. В ходе теоретикоэкспериментальных исследований решен комплекс перечисленных ниже частных задач исследования [3, 4].

• 1)    Анализ требований, предъявляемых к современным космическим аппаратам с прецизионной стабилизацией, в зависимости от их назначения и устанавливаемой на них научной аппаратуры. Цель — унификация этих требований.

• 2)    Классификация и анализ основных источников внутренних возмущений. Цель — определение наиболее виброактивных и выявление возможности ослабления и (или) исключения их воздействия.

• 3)    Обоснование и разработка экспериментальных методов и средств определения микровозмущений, а также методов их математического моделирования.

• 4)    Проведение экспериментов по определению диссипативных свойств конструкций космических аппаратов при малых уровнях перемещений (порядка 0,5 мкм).

• 5)    Обоснование и разработка достаточно точных математических моделей космических аппаратов и

• научной аппаратуры для анализа динамической точности как в низкочастотной, так и в среднечастотной областях возмущений.

• 6)    Обоснование и разработка методов математического моделирования для исследования динамической точности с учетом экспериментально определяемых параметров возмущений.

• 7)    Анализ результатов исследования динамической точности и общих требований к ее параметрам для перспективного космического аппарата, включая ЦА. Обоснование и разработка на основе этого анализа частных требований по виброактивности основных источников внутренних возмущений.

Материалы и методы

Постановка задачи исследования. Предложены схемы экспериментальных установок, реализация которых с применением метода обезвешивания позволяет воссоздать условия, максимально соответствующие реальной эксплуатации перспективных КА, ПЭК, ЦА и их приводов [3–5]. Математическое моделирование и эксперименты позволили обосновать и разработать предложения по коррекции динамических характеристик ПЭК и ЦА перспективных КА при действии внутренних источников возмущений.

Методы решения задачи исследования. Для решения задач исследования использованы методы математического моделирования, методы механики и динамики машин. Предложены: метод моделирования динамических характеристик перспективных КА при функционировании в режиме прецизионной ориентации с учетом работы штатных осцилляторов и метод обработки результатов экспериментальных исследований микровозмущений.

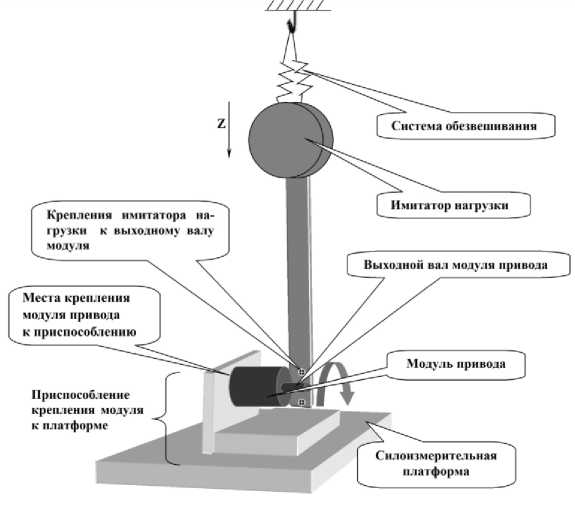
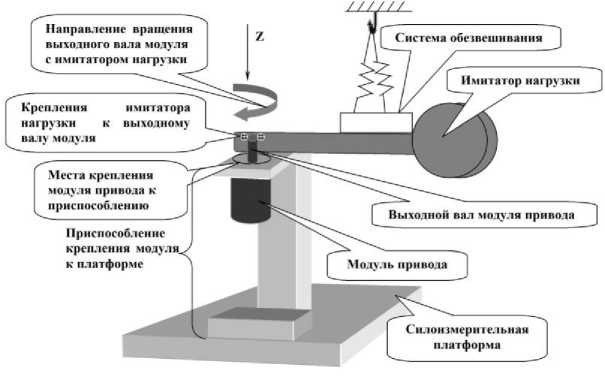
Описание схем экспериментальных установок. Для решения указанных задач реализованы схемы проведения экспериментальных исследований (рис. 1).

а )

Машиностроение и машиноведение

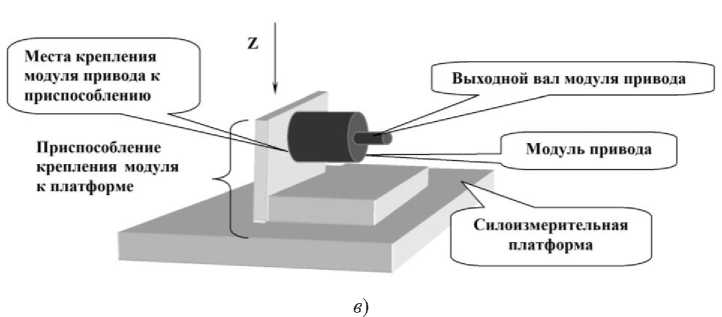
Рис. 1. Схемы проведения эксперимента на силовом испытательном стенде с нагрузкой на выходном валу модуля привода: горизонтальная ось вращения ( а ); вертикальная ось вращения ( б ); нагрузка на выходном валу J = 4,75 кгм² ( в )

Экспериментальные исследования по выбранным схемам позволили оценить влияние гравитации и системы обезвешивания на полезный сигнал [5-8].

Результаты исследования

Метод моделирования динамических характеристик приводов перспективных космических аппаратов с учетом функционирования штатных осцилляторов. Для обеспечения динамической точности принят представленный на рис. 2 порядок проведения исследований [8-11].

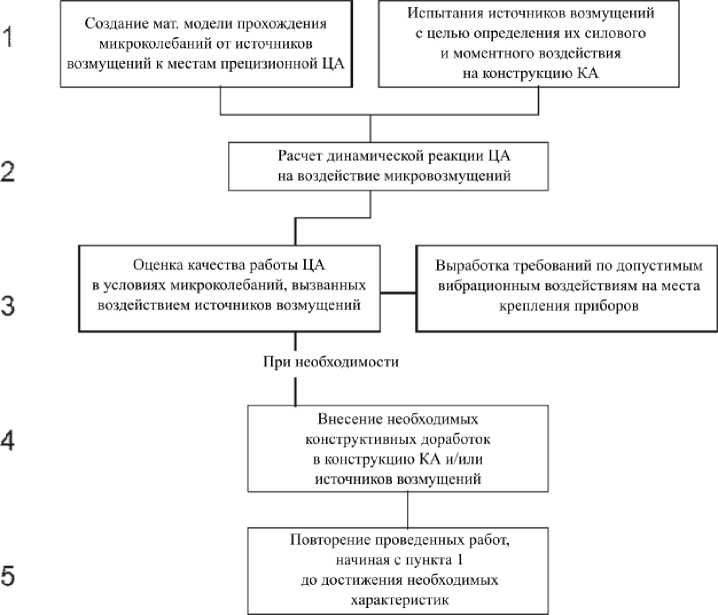
Рис. 2. Порядок проведения исследований, принятый при отработке динамической точности

Кроме того, экспериментально исследованы микровозмущения физических натурных моделей перспективных КА. При анализе информации, получаемой при экспериментальной отработке активных и пассивных осцилляторов, возникают проблемы идентификации динамических параметров математической модели изделия. В данной статье представлены пути и методы решения этих проблем.

Метод обработки результатов экспериментальных исследований микровозмущений перспективных КА. Метод определения основных параметров динамической схемы основывается на предположении, что полученная выборка свободного движения представляет собой общее решение системы линейных дифференциальных уравнений, то есть имеет вид [3, 4, 7, 8]:

y ⁽ t ) = S A je^bj Sin(2 n j + ф j ),                                   (1)

j = 1

где n — общее число искомых составляющих в выборке; A j — амплитуда вклада j -го тона; 5 j — декремент затухания j -го тона; f — частота j -го тона колебаний; ф j — фаза j -го тона колебаний; t — время.

Необходимо максимально приблизить эту зависимость к колебательной части сигнала с прибора, полученного по каналам телеметрии [7, 8]. Для фиксации идентифицируемого сигнала нужно провести следующие предварительные операции [3, 4, 7, 8, 10, 11]:

• —    выделить участок телеметрической информации по угловым скоростям или углам, где наблюдаются колебания, определяемые влиянием жидкого наполнения;

• —    удалить из полученного сигнала низкочастотные и постоянные составляющие, обусловленные угловым движением космического аппарата относительно его центра масс (производится путем фильтрации низкочастотной составляющей и (или) удалением полиномиального тренда, соответствующего твердотельным формам движения изделия);

• —    привести сигнал к постоянному интервалу регистрации;

• —    определить частотные диапазоны основных гармонических составляющих сигнала на основе использования алгоритма быстрого преобразования Фурье;

• —    сместить сигнал, чтобы время первого замера в исследуемой части сигнала соответствовало началу временной оси (это необходимо для правильной оценки диссипативных и фазовых характеристик).

Преобразованный таким способом сигнал используется в качестве таблично заданной функции ( x i ) при его аппроксимации зависимостью для определения параметров процесса. При подборе параметров используется метод наименьших квадратов. Параметры A j , 5 j , f и ф j определяются путем минимизации [3, 4, 7, 8]:

mn

S ⁽ x - Е ^Aj e -⁵ ' ^Х t ^{sin (2} п j + Ф j ^{)) 2} ^ ^min ,                           ⁽²⁾

i = 1       j = 1

где x i — значения сигнала, полученного при обработке результатов испытаний; t i — моменты времени, соответствующие замерам x i ; m — количество замеров; A j — амплитуда вклада j -го тона; 5 j — декремент затухания j -го тона; f j — частота j -го тона колебаний; ф j — фаза j -го тона колебаний.

Результаты моделирования и экспериментальные исследования учитывают следующие основные факторы:

• —    количество гармонических составляющих, проявляющихся в исследуемой выборке ;

• —    близость расположения частот этих составляющих;

• —    длина выборки (определяет и позволяет достоверно оценить необходимое число периодов движения по самой низкой частоте);

• —    шаг записи сигнала (определяет необходимое число точек на периоде движения самой высокой частоты) ;

• —    разброс амплитуд отдельных движений составляющих выборки;

  Машиностроение и машиноведение

  
  

• —    наличие в выборке ненаблюдаемых входных воздействий.

Разумеется, все перечисленные факторы взаимозависимы, а их влияние на точность и достоверность результата определяется их сочетанием. Поэтому исследование проводится для каждого фактора при вариации остальных.

Созданный метод апробирован при работе осцилляторов, в результате которой силовые факторы воздействуют на места крепления. При определении амплитудно-частотных характеристик (АЧХ) сил и моментов (работа модуля на штатной частоте импульсов шагового двигателя (ШД) 130 Гц) с учетом кинематической цепи конструкции применялась следующая последовательность разработки модуля:

• —    выбор из массива данных наиболее характерных результатов измерений (критерии выбора — максимальные амплитуды измеренных силовых параметров и максимальный набор пиков в АЧХ силовых параметров);

• —    анализ результатов измерений внешнего фона и колебаний систем крепления и обезвешивания в частотной области с целью выявления частот шумовых сигналов;

• —    составление списка диапазонов шумовых частот для каждого силового параметра;

• —    фильтрация из исходных процессов изменения силовых параметров в выбранных результатах измерения шумовых диапазонов частот (используется специальный пакет прикладных программ);

• —    сохранение результатов измерения отфильтрованных процессов и анализ их спектров с целью выявления основных осцилляторов кинематической цепи модуля.

Отдельные этапы разработки модуля описаны в [3, 4, 7, 8, 10, 11].

По представленным на рис. 1 схемам были проведены измерения сил и моментов, приходящих на места крепления модуля, для трех вариантов нагрузки на выходной вал со значениями момента инерции: 1) J 1 = 1,53 кгм²; 2) J ₂ = 6,1 кгм²; 3) J ₃ = 7,6 кгм².

Цель экспериментов — определить, как максимальные значения крутящего момента относительно оси вращения выходного вала зависят от величины момента инерции нагрузки на валу, а затем составить прогноз по величине крутящего момента для штатной нагрузки. При определении этой зависимости и крутильной жесткости на выходном валу модуля к анализу принимались измерения момента M z относительно оси вращения выходного вала.

Крутильная жесткость определялась по формуле:

c = J_t 4 п ² fi ²,                                                    (3)

где J _i — момент инерции нагрузки на выходном валу, кгм²; f — низшая частота крутильных колебаний относительно оси вращения выходного вала, Гц; i — номер варианта нагрузки на выходной вал модуля.

Из полезного сигнала момента M z (фильтрации) выделили процесс, в котором изменение данного момента происходит на низшей собственной частоте крутильных колебаний. Это позволило определить декременты колебаний.

Декременты крутильных колебаний выходного вала на низшей собственной частоте с различными вариантами нагрузки определялись по формуле:

5 = ¹ ln( A m I A m + n ) ,                                              (4)

n где Am — амплитуда ускорения на m-м цикле колебаний; Am + n — амплитуда ускорения на (m + n)-м цикле колебаний; n — число принятых к анализу циклов колебаний.

При определении жесткости выходного вала и декрементов крутильных колебаний на низшей собственной частоте применялась описанная ниже последовательность действий.

• 1)    Выбор трех наиболее характерных процессов изменения момента M z для трех вариантов нагрузки на выходном валу модуля.

• 2)    Определение низшей собственной частоты крутильных колебаний. В этом случае по максимальной амплитуде в АЧХ момента M z определяется частотный диапазон, в котором предположительно находится значение низшей собственной частоты крутильных колебаний. С помощью узкополосной фильтрации анализируются узкие диапазоны частот в выбранной области (критерием низшей собственной частоты крутильных колебаний среди анализируемых отфильтрованных процессов является монотонное убывание амплитуды во времени и отсутствие биений).

• 3)    По значениям низшей собственной частоты крутильных колебаний и момента инерции нагрузки с использованием формулы (3) определяется жесткость выходного вала.

• 4)    Из полученного временного процесса изменения амплитуд крутильных колебаний на низшей собственной частоте определяются значения A m , A m _{+ n} , n , а по формуле (2) — декремент этих колебаний.

Особенности обработки результатов исследований воздействия на места крепления со стороны силовых факторов, возникающих при работе осцилляторов. Автоматически выполняется преобразование формата первичных данных измерений в формат, удобный для графического представления и анализа информации. Применение специальной программы позволяет значительно сократить время первичной обработки результатов измерений. Для исключения из исходного процесса шумовых сигналов также используется пакет специальных прикладных программ.

Для каждого из измеренных силовых параметров ( F x , F y , F z , M x , M y , M z ) характерны не только общие для всех них шумовые сигналы (например, сетевая электрическая помеха на частоте ~50 Гц или стабильное внешнее возмущение грунта в диапазоне частот от 16 до 17,5 Гц), но и собственные, обусловленные влиянием систем обезвешивания и крепления привода. Для каждого из силовых параметров требуется исключить в среднем двенадцать частотных диапазонов. Соответственно, в каждой выбранной для анализа совокупности результатов измерений требуется исключение разных наборов шумовых сигналов для каждого из силовых параметров, если решается задача определения динамических характеристик модуля с учетом кинематической цепи (при этом необходим анализ измеренных силовых параметров в широком диапазоне частот от 0 до 200 Гц). Критериями выбора результатов измерений силовых факторов являются: максимальные амплитуды силовых параметров; максимальный набор пиков в амплитудно-частотных характеристиках силовых параметров.

При обработке результатов измерений в задаче определения жесткости модуля на выходном валу и декремента колебаний на низшей собственной частоте необходимо из исходного сигнала (фильтрации) выделить процесс, в котором изменение силового параметра происходит на низшей собственной частоте крутильных ко- лебаний. Эта процедура успешно реализуется в специальном пакете прикладных программ [3-4].

Методика выбора характерных режимов испытаний и соответствующих им результатов измерений. Основные схемы испытаний и режимы работы (частота импульсов шагового двигателя (ШД) 130 Гц) модуля были выбраны с учетом максимального приближения к условиям функционирования КА на орбите. Критериями выбора наиболее характерных режимов для решения поставленной задачи являются: — отсутствие нагрузки на выходном валу;

— вертикальная ось вращения выходного вала;

— частота опроса данных измерений не менее 500 Гц (исследуемый диапазон частот — от 0 до 200 Гц).

Критериями выбора результатов измерений для определения динамических характеристик модуля с учетом кинематической цепи являются:

— максимальные амплитуды измеренных силовых параметров;

— максимальный набор пиков в АЧХ силовых параметров.

Методика выбора характерных режимов и результатов измерений для определения жесткости и декремента крутильных колебаний выходного вала модуля. Критериями выбора характерных режимов для решения поставленной задачи являются:

— вертикальная ось вращения выходного вала (см. рис. 1, б);

— три варианта нагрузки на выходном валу (величина нагрузки не менее 0,5 кгм2);

— частота опроса данных измерений не менее 50 Гц (исследуемый диапазон частот — от 0 до 10 Гц).

Критерием выбора файлов являются максимальные амплитуды измеренного момента M z .

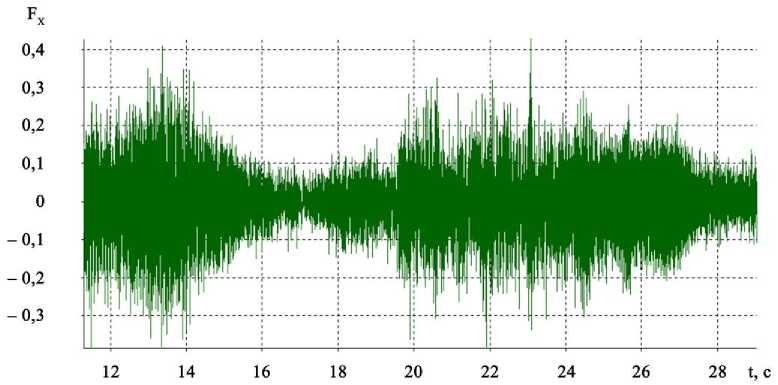
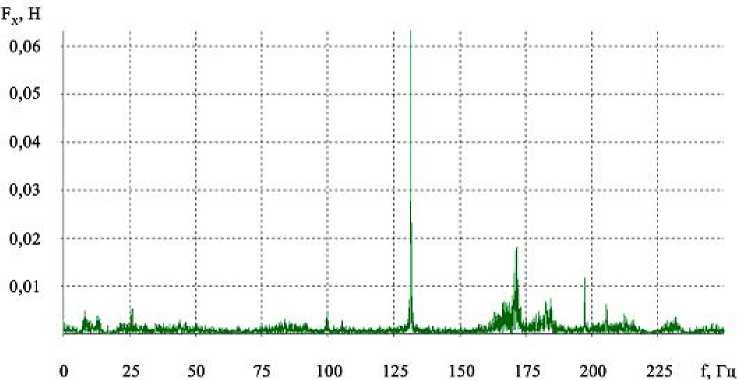
Методика определения динамических характеристик модуля с учетом кинематической цепи. После обработки исходного измеренного сигнала формируется полезный сигнал, отражающий динамику звеньев кинематической цепи модуля при работе ШД на частоте управляющих импульсов 130 Гц. Анализ АЧХ каждого из силовых параметров ( F x , F y , F z , M x , M y , M z ) позволил выявить основные диапазоны частот, на которых имели место повышенные амплитуды этих параметров. В результате проведенных исследований определены временные процессы и спектры для сил F x , F y , F z и моментов M x , M y , M z . На рис. 3 представлены примеры временных процессов и спектров для силы F x и момента M x .

б )

Машиностроение и машиноведение

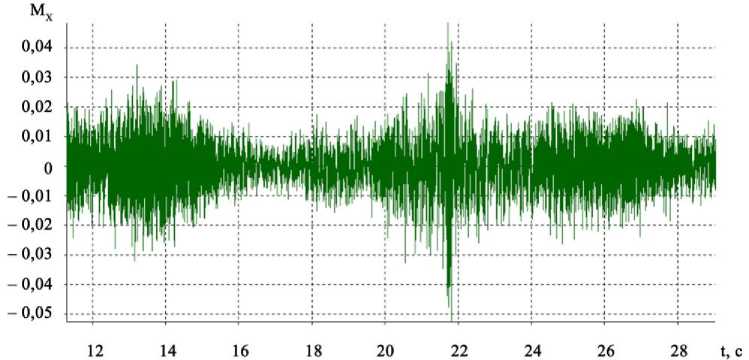
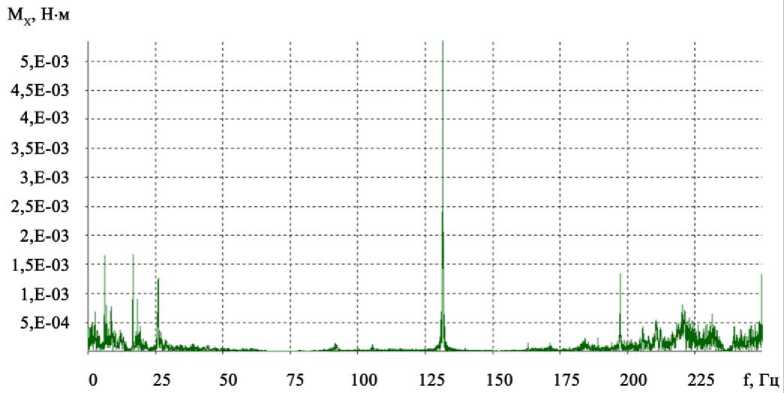
Рис. 3. Временной процесс ( а ) и спектр ( б ) силы F x ; временной процесс ( в ) и спектр ( г ) момента M x на частоте ШД 130 Гц

Результаты определения динамических характеристик модуля на низшей собственной частоте крутильных колебаний выходного вала. Результаты расчетов приведены в табл. 1.

Таблица 1

Частотные характеристики по параметрам сил Fx, Fy, Fz и моментов Mx, My, Mz при работе модуля на частоте импульсов ШД 130 Гц

№ п/п	Параметр нагрузки	Частота f , Гц (в скобках указано осредненное значение амплитуды нагрузки)
1	F x , Н	0,5÷0,9 (0,014); 5÷6,1 (0,08); 8,2 (0,04); 12,3 (0,03); 26,2 (0,04); 45 (0,022); 91(0,02); 105 (0,014); 130 (0,39); 170 (0,01); 205 (0,04)
2	F y , Н	5÷6,1 (0,014); 8,2 (0,02);12,3 (0,02); 26,2 (0,044); 45 (0,014); 91 (0,017); 130 (0,47); 170 (0,02); 205(0,04)
3	F z , Н	0,5÷0,9 (0,07); 26,2 (0,04); 45 (0,015); 91 (0,04); 130 (0,1); 170 (0,02)
4	M x , Нм	0,5÷0,9 (0,01); 8,2 (0,0025); 12,3 (0,03); 26,2 (0,025); 91 (0,0026); 105 (0,003); 130 (0,3); 170(0,001); 205 (0,0045)
5	M y , Нм	5÷6,1 (0,016); 8,1 (0,0062); 26,2 (0,016); 45 (0,004); 91 (0,008); 105 (0,005); 130(0,075); 170 (0,01); 205 (0,0055)
6	M z , Нм	0,5÷0,9 (0,0025); 5÷6,1 (0,005); 18,5 (0,004); 26,2 (0,011); 45 (0,006); 105 (0,0018); 130 (0,3); 170 (0,015)

После обработки исходных измеренных сигналов по предложенной методике получены данные для определения жесткости выходного вала по формуле и декрементов крутильных колебаний. Анализ крутильных колебаний выходного вала модуля проводился для моментов инерции: 1,53 кг·м 2 ; 6,1 кг·м 2 ; 7,6 кг·м 2 . При исследованиях крутильных колебаний выходного вала модуля сравнивались две ситуации:

• —    ШД включен и кинематическая цепь в работе;

• —    ШД выключен.

В первом случае низшая собственная частота крутильных колебаний ниже, чем во втором. Результаты анализа приведены в табл. 2.

Таблица 2

Результаты определения жесткости выходного вала модуля с нагрузкой на низшей собственной частоте

Момент инерции нагрузки, кг·м 2	Низшая собственная частота системы, Гц		Жесткость выходного вала, Н·м/град
		При работе модуля		При работе модуля
1,53	6,2	5,3	40,5	29,6
6,1	2,63	2,34	29,1	23
7,6	2,44	2,1	31,2	23,1
29	1,22	1,07	31	23

Полученные осредненные величины амплитуд моментов Mz и декрементов колебаний для низших собственных частот системы приведены в табл. 3.

Таблица 3

Декременты крутильных колебаний и осредненные амплитуды момента относительно оси вращения выходного вала

Примеры временного процесса момента Mz и его спектра для случая нагрузки на выходном валу модуля J ₂ = 7,6 кгм² представлены на рис. 4.

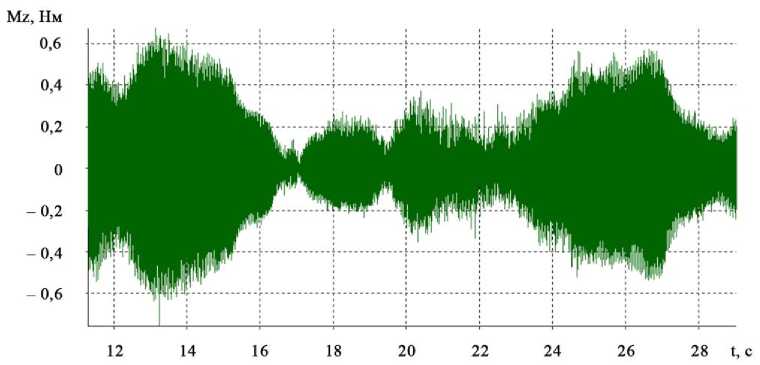
а )

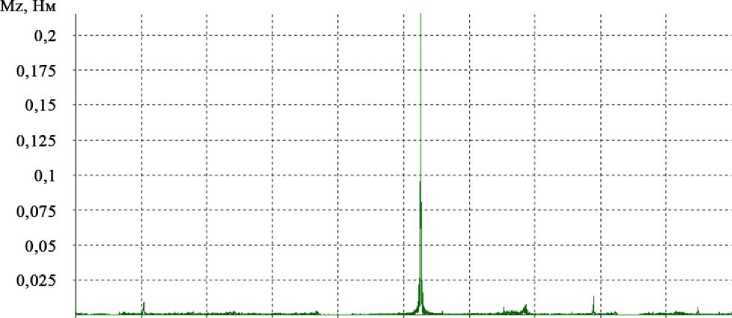
О 25      5 0      7 5      1 00     125     150      1 75     200     225 f, Гц

б )

Рис. 4. Графики временного процесса ( а ) и спектра ( б ) момента Mz для случая нагрузки на выходном валу модуля J ₂ = 7,6 кгм²

Машиностроение и машиноведение

Момент инерции нагрузки, кг·м 2	Амплитуда Mz , Н·м	Декремент колебаний
1,53	0,022	0,06
6,1	0,115	0,14
7,6	0,14	0,14
29	∼ 0,5	0,14

Обсуждение и заключения. Исследования позволили определить динамику приводов перспективного КА и его составных частей как источников внутренних возмущений. Анализ результатов исследований показал, что для снижения влияния активных осцилляторов на динамическую точность перспективного КА в режиме прецизионной ориентации необходимо:

• —    провести экспериментальное подтверждение исходных данных по бортовым источникам возмущений;

• —    провести экспериментальное исследование диссипативных характеристик и характеристик жесткости конструкции перспективного КА;

• —    разработать критерии оценки влияния воздействий от бортовых источников возмущений на целевое функционирование перспективного КА в диапазоне частот до 100 Гц;

• —    уточнить среднечастотную динамическую модель перспективного КА по результатам экспериментальных исследований;

• —    провести анализ чувствительности бортовых приборов перспективного КА к вибрациям и разработать требования к виброактивности источников микровозмущений;

• —    провести определение виброактивности источников вибровозмущений: двигателя-маховика (ДМ), привода зеркала МСУ-ГС, измерителя солнечной постоянной ИСП-2М.

Результаты проведенных теоретико-экспериментальных исследований позволили решить перечисленные ниже задачи.

• 1)    Анализ источников микровозмущений:

• —    анализ состава, режимов работы и характеристик бортовых источников микровозмущений;

• —    оценка вибровозмущений конструкции КА, генерируемых электромеханическими исполнительными органами (ЭМИО);

• —    оценка моментов, создаваемых ДМ по командам системы управления ориентацией и стабилизацией (СУОС); — оценка вибровозмущений конструкции КА, генерируемых многозональным сканирующим устройством гидрометеорологического обеспечения (МСУ-ГС);

• —    оценка вибровозмущений конструкции КА, генерируемых приводом солнечной батареи (СБ);

• —    оценка вибровозмущений конструкции КА, генерируемых приводом остронаправленной антенны (ОНА);

• —    оценка вибровозмущений конструкции КА, генерируемых измерителем солнечной постоянной величины (ИСП-2М).

• 2)    Оценка динамических характеристик посадочных мест гироскопического измерителя вектора угловой скорости (ГИВУС) перспективного КА при вибрационных воздействиях от ИСП-2М, а также от:

— МСУ-ГС,

— ДМ (вибрации обусловлены командами СУОС и остаточным дисбалансом).

• 3)    Оценка динамических характеристик посадочного места МСУ-ГС перспективного КА при возмущениях от ДМ по командам СУОС, ДМ, обусловленных остаточным дисбалансом, ИСП-2М.