Теоретические основы представления сигнала в аналитическом виде функциями его огибающей и полной фазы

Методы частотно-временной обработки находят все более широкое практическое применение в различных областях радиотехники. Большинство работ, посвященных указанной проблематике, как правило, начинаются с анализа свойств функции Вигнера, которая базируется на понятии аналитического представления комплексного сигнала (аналитического сигнала). Практическое удобство его использования в алгоритмах синтеза частотновременных распределений (ЧВР) несколько затенило теоретический аспект использования аналитического сигнала в качестве инструмента анализа сложных процессов. В связи с этим цель данной работы — в строгом теоретическом обосновании подхода, позволяющего обобщить традиционное представление аналитического сигнала функциями его огибающей и полной фазы (здесь и ниже выражение "функции огибающей и полной фазы" следует понимать как "функции, представляющие огибающую сигнала и полную фазу сигнала") в частотно-временном пространстве.

АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛА ФУНКЦИЯМИ ЕГО ОГИБАЮЩЕЙ

И ПОЛНОЙ ФАЗЫ

Совершенствование технологий цифровой обработки сигналов обусловило эффективность применения многих алгоритмов частотно-временного анализа, связанных с синтезом совместных представлений плотности распределения энергии в пространстве частота—время, которые в свою очередь базируются на понятии аналитического сигнала z_a ( t ) [1]:

za (t) = z(t) + jZ(th где z(t) и z(t) — в общем случае функции, свя занные между собой преобразованием Гильберта:

z (t) = -lj zT d, ;    -z( t) = lj

πt - τπt

-∞-∞

Согласно (2), основное различие сигналов z ( t ) и z ( t ) состоит в том, что их спектральные составляющие сдвинуты относительно друг друга на п /2. В [1-3] подробно изучены свойства аналитического сигнала и рассмотрены особенности формирования на его основе ЧВР класса Коэна.

Представление сигнала в аналитической форме в первую очередь связано с удобством его описания. Так, если рассматривать, опираясь на понятие (1), в общем случае произвольный сигнал в виде квазигармонического колебания za(t) = A(t )exP{ j0( t)},                (3)

то его огибающую (рис. 1) можно представить как функцию

A (t) = \ z 2( t) + z 2( t), а полную фазу рассчитать в соответствии с

0( t ) = arctg zt ). z ( t )

При таком определении A(t) и 0 (t) следует выполнение условий:

dz (t) = dA (t) dt       dt ’ d0( t) = z'( t) z (t) - z'(t) z( t)

d t          z ²( t ) + z ²( t )

т. е. сигнал будет совпадать с функцией огибающей в точках, где 0 ( t , ) = 0,2 п , 4 п ,...

точек t_i будет выполняться равенство

z( ⁽ t )

t

Рис. 1. Сигнал z ( t ) и функция его огибающей A ( t )

d z ( t ) = d[ A ( t )] d t d t

. t = t ,

Физический смысл указанных понятий заключается в том, что огибающая A ( t ) представляет функцию, связывающую совокупность точек сигнала, в которых фаза меняет знак. В свою очередь, фаза сигнала 6 ( t ) представляет функцию, характеризующую закон изменения сигнала в точках его экстремума. Следовательно, мгновенную частоту сигнала (3) можно рассматривать как величину, пропорциональную скорости изменения фазы

С учетом периодичности функции cos полученное равенство будет выполняться при 6 ( t , ) = 0,2 n , 4 n ,...

Утверждение 2

Для колебания вида z ( t ) = A ( t )cos( 6 ( t )) (где A ( t ) — функция огибающей z ( t ), а 6 ( t ) — полная фаза z ( t )) и его комплексно-сопряженной формы z ( t ) = A ( t )sin( 6 ( t )) справедливо выполнение следующего условия: производная от функции полной фазы равна отношению

П t ) z ( t ) - z 't, t ) z ( t )

z ²( t ) + z ₍ t )     ■

f ( t ) =

1 d 6 ( t )

2 n d t

Из предложенного подхода следует, что z(t) = A(t)cos(6(t)), а z(t) = A(t) sin(6(t)).     (7)

Докажем выполнение условия (7) для равенств (4) и (5).

Утверждение 1

Для колебания вида z ( t ) = A ( t )cos( 6 ( t )), где A ( t ) — его огибающая, а 6 ( t ) — фаза, справедливо выполнение условия: производная от функции сигнала в общем случае равна значению производной от функции его огибающей.

Доказательство

Распишем значение производной от функции исходного сигнала:

Доказательство

Распишем указанное условие с учетом аналитического описания исходного сигнала и его комплексно-сопряженной формы:

~z'( t) z (t) - z'(t) z( t) = z 2( t) + z 2( t)

= { A '( t ) sin[ 6 ( t )] + A ( t ) 6 '( t ) cos[ 6 ( t )]} A ( t ) cos[ 6 ( t )]

A ² ( t ) cos² [ 6 ( t )] + A ² ( t ) sin² [ 6 ( t )]

{ A '( t ) cos[ 6 ( t )] - A ( t ) 6 '( t ) sin[ 6 ( t )]} A ( t ) sin[ 6 ( t )] =

A ² ( t ) cos² ( 6 ( t )) + A ² ( t ) sin² [ 6 ( t )]           =

= {cos^J 6 W] + sln^J 6 WMI t ) 6 t t ) = ₆ -_tt )

A ²( t ){cos²[ 6 ( t )] + sin²[ 6 ( t )]}        ^U.

Физическая сущность мгновенной частоты и огибающей принципиально отличается от частоты и амплитуды, используемых для представления сигнала с помощью ряда обобщенного описания [2]

TO z (t) = 2^ Ak k=0

(2nk . .

cos ---- 1 +

I T

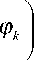
или его интегральной формы

d z ( t ) = d[ A ( t )cos( 6 ( t ))] d t            d t

d[ A ( t )]                   d[ 6 ( t )] .

= ^v cos[ 6 ( t )] - A ( t )—— sin[ 6 ( t )]. d t                      d t

Учитывая, что функции cos и sin ортогональны, следовательно, всегда существуют такие точки t , , в которых cos[ 6 ( t , )] = 1, а соответственно sin[ 6 ( t , )] = 0. Отсюда следует, что для указанных

TO

z ( t ) = 2 J { A ( f )cos[2 n ft + Ф( f )]}d f .             (9)

Так, например, согласно ряду (8), определяемое колебание представляет совокупность гармоник, частота и амплитуда которых неизменны на всем протяжении оси t от -то , до то , даже если само рассматриваемое колебание существует только в ограниченном временном интервале. Отсутствие же энергии вне сигнального интервала в этом случае

объясняется тем, что спектральные компоненты базисных гармоник в совокупности равны нулю.

С позиций описания сигнала на основе его мгновенной частоты и функции огибающей в каждый момент времени он будет иметь только одну частотную составляющую, определяемую выражением (6), в то время как его спектр может иметь множество различных спектральных компонент. Но в отличие от неизменных величин, определяющих сигнал — частот и амплитуд базисных функций, значение мгновенной частоты может непрерывно меняться во времени.

ДВУМЕРНЫЕ ПРЕДСТАВЛЕНИЯ ФУНКЦИИ ОГИБАЮЩЕЙ АНАЛИТИЧЕСКОГО СИГНАЛА

Развитие теории синтеза ЧВР однозначно связано с понятием комплексной плотности распре-

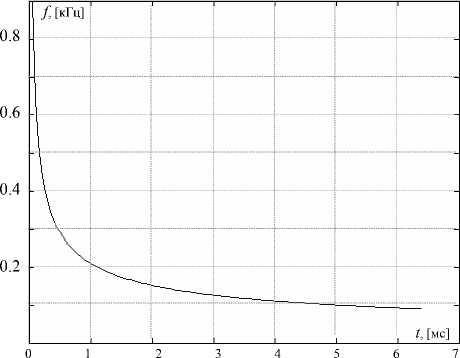
Рис. 2. Идеальное частотно-временнóе распределение тестового сигнала деления энергии, получаемой в результате комплексного произведения аналитического сигнала za (t) и его спектра Fa(f)

ρ R ( f , t ) = z a ^∗ ( t ) F a ( f ) e^{j 2 π ft} . (10)

Распределение вида (10) называют ЧВР Риха-чека [4]. Так, на рис. 2 представлено идеальное ЧВР тестового сигнала, а на рис. 3 — распределение тестового сигнала, полученное на основе выражения (10).

Анализ результатов, представленных на рис. 3 показывает, что помимо истинных компонентов энергии тестового сигнала, расположенных вдоль линии его мгновенной частоты, на плоскости ЧВР присутствуют и так называемые интерференционные компоненты, представляющие результат совместного взаимодействия сигнальных отсчетов, составляющих анализируемый процесс в полосе анализа.

С целью подавления "паразитных" выбросов сигнальной энергии в [5] предложено использовать так называемые псевдораспределения, в которых для расчета "единичной" частотно-временнόй площадки в каждый момент времени задействуются только сигнальные компоненты, попадающие во временнόй интервал, ограниченный функцией окна, например Хемминга. Общность такого подхода базируется на рассмотрении псевдораспределения как некоторой сглаженной версии исходного комплексного ЧВР. На практике большее применение нашло распределение функции активной энергии, представляющее реальную часть ЧВР Рихачека [4]

ρ A ( f , t ) = 0.5Re[ ρ R ( f , t )]. (11)

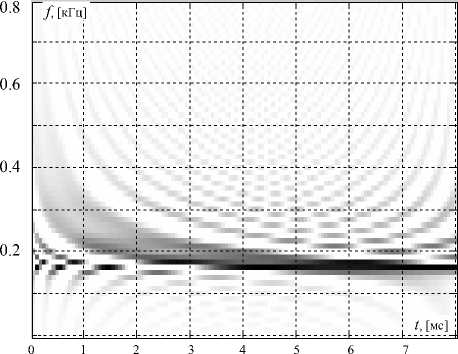
Рис. 3. Частотно-временнóе распределение Риха-чека тестового сигнала

Рис. 4. Псевдо-ЧВР функции активной энергии тестового сигнала

Так, на рис. 4 показан результат представления тестового сигнала на основе его псевдоформы.

Поскольку распределение энергии (11) в общем случае характеризуется мгновенным значением, то, очевидно, к нему применимо понятие огибающей. Однако в этом случае она будет представлена функцией двух переменных — частоты и времени. Тогда в соответствии с утверждением 1 аналитическое описание огибающей функции распределения энергии будет иметь следующий вид:

O m ( f , t ) = V{ ^Re [ P r ( f , t ) ] } 2 ⁺{ l^m [ P r ( f , t ) ] } ² . (12)

Следует заметить, что полученные аналитические выражения для ЧВР имеют место только в отношении узкополосных сигналов, значение нижней границы спектра f_H которых значительно превышает занимаемую ими полосу частот:

f H > AF .                   (13)

В [3] уточнено само понятие узкополосного сигнала. Вместо традиционно принятого неравенства AF << f, допускается f, > 1.5AF ,                   (14)

где f , — средняя частота в спектре сигнала. Корректность использования функции огибающей распределения в качестве адекватного представления плотности энергии в частотно-временном пространстве основывается на доказательстве следующего утверждения.

Утверждение 3

Для колебания вида z ( t ) = A ( t )cos[ 0 ( t )], где A ( t ) и 0 ( t ) соответственно функции огибающей и фазы, значение производной его функции плотности распределения мгновенной энергии вида P M ( f , t ) = 2 z ( t ) X ( f , t ) равно представлению производной огибающей колебания в двумерном тригонометрическом частотно-временном базисе разложения X ( f , t ) = [ a t ( f ) cos(2nft) + b t ( f )sin(2 nft )]:

d p M ( f , t ) _ d[2 z ( t ) X ( f , t )] _ d A ( t )

-----------=----------------- = 2------X ( f , t ) .

d t              d t             d t

Доказательство

Представим производную функции плотности распределения мгновенной энергии в следующем виде:

^{d p M ( f} ’ t ) = 2^^ cos[ 0 ( t )] x d t          d t

x [ a t ( f ) cos(2 n ft ) + b t ( f ) sin(2 n ft )] -

• - ² A ⁽ t ) — ) [ ^{a ( f} ) c°^{s(2 n} ft ) - b t ^{( f} )^{sin(2 n} ft ^)] - d t

• -4n ft • A ( t )cos 0 ( t ) x

x [ a t ( f ) sin(2 n ft ) - b_t ( f ) cos(2 n ft )].

Функции базиса разложения cos и sin ортогональны, следовательно, всегда существуют такие точки ti , в которых функция cos[0(ti)] = 1, а соответственно sin[0(ti)] = 0 . Тогда dpM(f, t) = dt

• = 2 d At ) [ a t ( f ) cos(2 n ft ) + b t ( f ) sin(2 n ft )] - d t

• -4n ft • A ( t )[ a t ( f )sin(2 nft ) - b t ( f )cos(2 n ft )].

При отсутствии частотных сдвигов вторая половина правой части равенства будет равняться нулю, в результате чего окончательно получим:

^{d p} M ^{( f} ’ t ) = 2 d A ⁷¹ X ( f , t ). d t          d t

Таким образом, в соответствии с утверждением (3) производная от функции распределения мгновенной энергии будет равна с точностью до постоянного множителя представлению производной от огибающей сигнала в двумерном тригонометрическом частотно-временном базисе разложения.

Особая привлекательность функции плотности распределения мгновенной энергии как инструмента анализа заключается в несмещенности оценок, получаемых на основе ее производной, в соответствии с утверждением 4.

Утверждение 4

Мгновенные оценки, получаемые на основе функции плотности распределения мгновенной энергии сигнала, являются несмещенными.

Доказательство

Допустим, что Pm (f, t) = 2z(t)X( f, t) — функция плотности распределения мгновенной энергии некоторого произвольного сигнала z(t), где X( f, t) = [at (f )cos(2n ft) + bt (f )sin(2n ft)] — двумерный тригонометрический частотно-временной базис разложения. Тогда dPM (f, t) = d[2z(t)X( f, t)] = dt              dt

= 2 •Г d z ^ t ) X ( f , t ) + z ( t )М^ .

_ d t                       d t    _

Решая данное уравнение, получим: dPM(f, t) = dt

= 2 ^{d z ( t )} [ a_t ( f )cos(2 πft ) + b_t ( f )sin(2 πft )] - d t

- 4 πft ⋅ z ( t )[ a_t ( f )sin(2 πft ) - b_t ( f )cos(2 πft )].

Для мгновенных оценок вторая половина правой части равенства может быть приравнена нулю, причем без всякого смещения по частоте. В результате чего будем иметь dρM(f,t)=2dz(t)Χ(f,t). dtdt

Таким образом, оценка, полученная на основе производной от функции распределения мгновенной энергии, является несмещенной и численно равна произведению производной сигнала и функ-

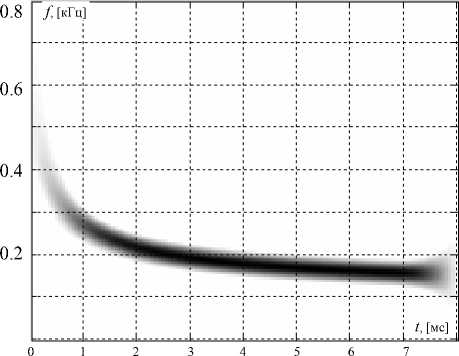
Рис. 5. Частотно-временнóе распределение огибающей функции мгновенной энергии тестового сигнала

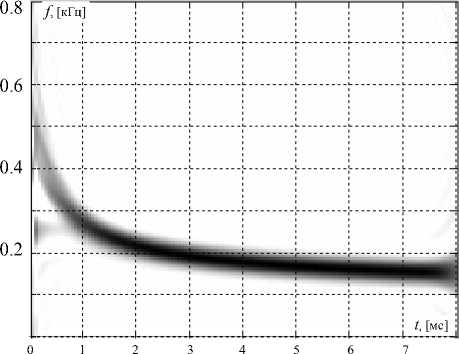
Рис. 6. Частотно-временнóе распределение плотности мгновенной энергии тестового сигнала ции тригонометрического частотно-временнόго базиса.

Проведенный в [3] анализ свойств распределения огибающей (12) показал, что приемлемые результаты его применения в качестве инструмента анализа удается получить только для узкополосных сигналов с низкой степенью нестационарно-сти поведения их параметров. Указанное обстоятельство обусловлено достаточно слабо выраженной степенью концентрации энергии в пределах обрабатываемой частотно-временнόй области. Так, на рис. 5 представлено распределение O_M ( f , t ) тестового сигнала.

Анализ полученных результатов позволяет сделать вывод, что в пределах от 1 мс до 7 мс (область относительно высокой стационарности) распределение (12) локализует энергию сигнала вдоль линии его мгновенной частоты с высокой степенью концентрации. В то же время на интервале от нуля до 1 мс (область относительно низкой стационарности) степень концентрации сигнальной энергии такова, что сложно говорить о характере изменения мгновенной частоты.

Справедливости ради необходимо отметить, что оценивание энергетических параметров нестационарных процессов непосредственно на основе распределения мгновенной энергии

ρ_M ( f , t ) = 2 z ( t )[ a_t ( f )cos(2 πft ) + b_t ( f )sin(2 πft )]

не лишено сложностей. Прежде всего — это наличие "паразитных" интерференционных компонент. Так, на рис. 6 представлено распределение ρ_M ( f , t ) тестового сигнала. Даже на основе визуального анализа можно заключить, что в районе частоты f = 200 Гц на плоскости ЧВР отчетливо просматривается ложный пик энергии, обусловленный тем, что в пределах "единичной" площадки взаимодействовали не только близлежащие сигнальные компоненты, но и находящиеся на более отдаленных частотных позициях.

ЗАКЛЮЧЕНИЕ

Несмотря на указанные недостатки рассмотренных распределений, последние наряду с другими совместными частотно-временными описаниями класса Коэна находят широкое применение в практических приложениях радиотехники [6–7]. Рассмотренные же в работе ЧВР были выбраны с целью наглядного представления полученных теоретических результатов, поскольку они достаточно полно характеризуют роль и значение функции огибающей и полной фазы аналитической формы представления сигналов для измерения и оценивания их параметров.