Теоретические основы процесса валки деревьев машинами, снабженными гибкими пильными цепями

Введение . Процесс валки дерева гибкими пильными цепями (ГПЦ) отличается от традиционных способов спиливания растущего дерева тем, что для ГПЦ нет необходимости в применении дополнительных и дорогостоящих валочных приспособлений, каковыми являются гидроклин, гидродомкрат, валочный рычаг, манипулятор.

В литературе рассмотрен вопрос падения дерева. Авторы [1–5] считают все части дерева абсолютно жесткими, поэтому допускают, что оно имеет всего одну степень свободы и падает в одной плоскости. В некоторых случаях подобное допущение возможно, однако в большинстве вариантов падающее дерево совершает более сложное движение в пространстве с некоторым вращением и отклонением фактической плоскости падения от геометрической. Особенно ярко это выражено при валке леса ГПЦ.

Для прямостоящих деревьев причиной падения является выход проекции центра тяжести за контур пня вследствие наклона ствола при изгибе недопила.

Рассмотрим расчетную схему положения ствола на пне в момент разрушения недопила (рис. 1).

Принимаем:

• 1.    Расстояние ВВ ¹ равно диаметру резца. При этом не учитываем отрезок В ¹ В ¹¹. Такое предположение допустимо и идет в запас устойчивости ствола.

• 2.    Точки О и О ¹ лежат на одной вертикали (реально точка О ¹ находится правее за счет общего смещения ствола вправо из-за изгиба недопила). То есть смещением центра тяжести за счет изгиба недопила пренебрегаем, что также идет в запас устойчивости ствола.

  

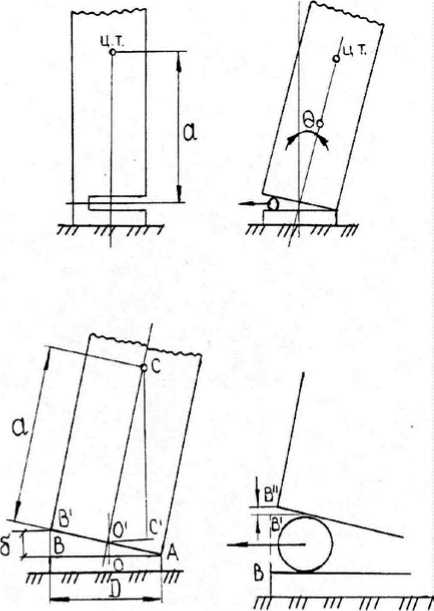
  Рис. 1. Расчетная схема положения ствола на пне в момент разрушения недопила

  
  

Из подобия треугольников АВВ ¹ и СС¹О¹ следует ∠ А = ∠ С = Θ 0 . Поскольку угол ВАВ¹ мал, то tg ∠ A = Sin ∠ C .

Из рисунка 1 видно, что ВВ ¹ / АВ = tg ∠ A , О¹О¹ /О¹С = Sin ∠ C , или

δ/D=tg ∠ A, O¹C¹=aSin ∠ C .                                         (1)

Из (1) получаем                  О¹С¹=аδ/D .                                                      (2)

Критерий начала падения дерева имеет вид: О¹С¹ > OA = D /2.

Учитывая (2), находим значение высоты, при которой дерево будет опрокидываться только от наклона, вызванного выходом ГПЦ из пропила.

a≥a кр , где а кр = D ²/2 δ .

Рассмотрим процесс падения дерева в многомерном пространстве при валке его гибкими пильными цепями.

Система отсчета. Введем неподвижную систему отсчета Oξηζ, выбрав начало в точке О , точке контакта ствола с пнем при падении. Направим ось Oη по направлению надвигания агрегата ГПЦ: ось Oξ вертикально вверх, ось Oζ так, чтобы тройка осей Oξηζ составляла Декартову систему координат (рис. 2).

Свяжем с падающей частью дерева подвижную систему отсчета O 1 XYZ с началом в точке O 1 пересечения оси дерева с плоскостью пропила. Далее пренебрегаем расстоянием между точками О и О 1 и приближенно считаем, что ось падающего дерева все время проходит через точку контакта O.

Тогда принимаем, что до начала пиления оси Oζηξ и OXYZ соответственно совпадают, а при наклоне ствола за счет изгиба недопила и при его падении положение системы отсчета OXYZ , жестко связанной с деревом, определяется относительно неподвижных осей Oζηξ с помощью углов Эйлера: Ψ – угла прецессии; ϕ – угла собственного вращения; Θ – угла нутации.

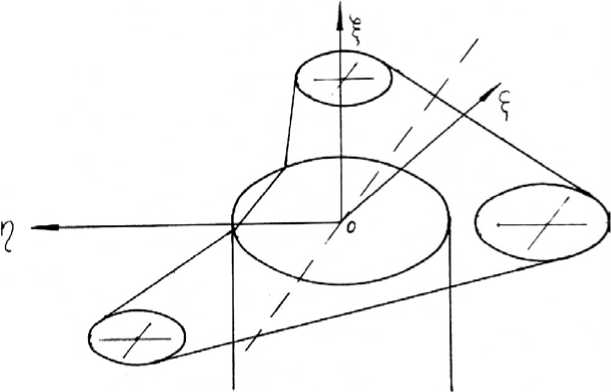
Рис. 2. Система координат в момент начала падения дерева

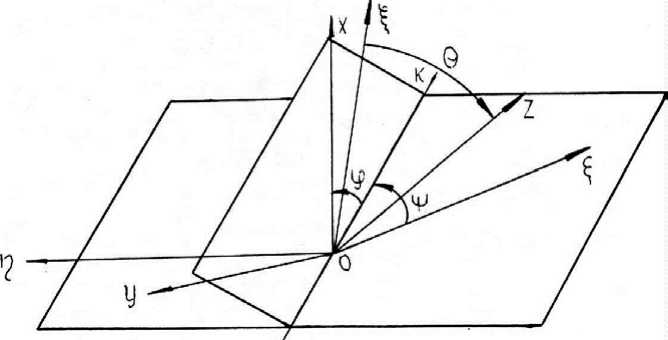
Рис. 3. Взаимодействие системы координат с прямостоящим деревом и деревом при падении

На рисунке 3 показана двойная система координат: первая связана с деревом в момент начала его падения, вторая отслеживает падение дерева, то есть постоянно связана с падающим деревом.

Линия ОК – параллельная линии пропила, она является осью нутации, вокруг нее поворачивается ось OZ на угол Θ ; Oξ – ось собственного вращения, вокруг которой поворачивается дерево на угол ϕ ; Oζ – ось прецессии, вокруг нее поворачивается на угол ψ вертикальная плоскость, в которой падает ось дерева, то есть плоскость, проходящая через оси Oξ и OZ .

Исходные предположения:

• 1.    Дерево является осесимметричным абсолютно жестким телом.

• 2.    При падении дерево имеет с пнем единственную и неподвижную точку контакта, положение которой со временем не изменяется.

• 3.    Ось симметрии дерева проходит через точку контакта, положение которой в пределах области среза пня безразлично по отношению к системе отсчета.

• 4.    Процесс падения начинается в момент разрушения недопила, при этом ось дерева имеет наклон Θ O , скорость Θ ^' o , обусловленную скоростью изгиба недопила, и скорость прецессии Ψ ^' O , вызванную действием ГПЦ на ствол в момент разрушения недопила.

• 5.    На дерево действуют только сила тяжести gm и силы реакции со стороны пня в точке опоры. Отсутствуют валочные устройства и приспособления, а следовательно, их усилия.

Основные уравнения, постановка задачи. При сделанных предположениях задача о процессе падения дерева при пилении ГПЦ сводится к задаче о движении абсолютно твердого тела, имеющего неподвижную точку в варианте Лагранжа-Пуассона.

• В    этом случае имеем шесть уравнений относительно шести функций ψ, ϕ , θ, ρ , q , r .

Adp/dt+(B-A)qr = gm α sinθsin ϕ

Adq/dt+(A-B)rp = -gm α sinθcos ϕ                               (4)

Bdr/dt = 0 ,

где α – расстояние от оси пиления до центра тяжести дерева; р = ψ sinθsinϕ+θcosϕ , q = ψ sinθcosϕ - θsinϕ , r = ϕ + ψ cosθ, и начальные условия:      ψθ =  ψο,      ψ'ο  =  ψ'ο,        ϕθ =  0,    ϕ'ο  =  0, (5) θο = θο,     θ 'ο = θ 'ο , где А, В – моменты инерции дерева относительно осей ОX и ОZ соответственно.

Решение поставленной задачи. Из системы (4) находим три первых интеграла:

где

A(p2+q2) = -2gm ∂ α cosθ+C 1 A(psin ϕ +qcos ϕ )sinθ+Brcosθ = C 2                            (6) r=C 3 , C 1 ,C 2 ,C 3 – произвольные постоянные. Подставив в (6) выражения для p,q,r, из (4) получим систему относительно углов ψ, ϕ ,θ . A(ψ2sin2θ+θ2)+2gm ∂ αcosθ=C 1 Aψ'sin2θ+BC 3 cosθ=C 2                                    (7) ψ'cosθ+ ϕ '=C 3 . Подставив ψ ' из второго уравнения (7) в первое, получим уравнение относительно θ: θ 2=((C 1 -2m ∂ gαcosθ)/A)-((C 2 -BC 3 cosθ)2/A2sin2θ .                        (8) Поскольку из (7) и (5) имеем:

C 1 =(Aψ 0 ²sin²θ 0 +θ 0 ²)+2gm ∂ αcosθ 0 ,

C 2 =Aψ ^' 0 sin²θ 0 +Bψ ^' 0 cos²θ 0 ,                                 (9)

C3=ψ'0cosθ0 , то уравнения (5) – (8) можно записать в виде θ'=ƒ1(θ),

где ƒ1(θ)=√ψ02sin2θ0+θ02+(2gm∂α/A(cosθ0-cosθ)-                         (10) -1/sin2θ[ψ'0sin2θ0+Β/Aψ'0cosθ0(cosθ0-cosθ)]2. Разделяя в (10) переменные, получим: dθ/ƒ1(θ)=dt , и поскольку t(θ0)=0 , находим t = θ∫ dθ .                     (11) θ0 f1 (θ) Второе и третье уравнения системы (7), учитывая (9), запишем в виде: ψ'=ƒ2(θ),      ƒ2(θ)=C2-BC3cosθ/Asin2θ, где ϕ'=ƒ3(θ),      ƒ3(θ)=C3-ƒ2(θ)cosθ, или в развернутом виде:

f 2( 0)=[sin² 0 _O+B/Aoss 0_o(oss 0_o-oss 0)] щ o /sin² 0

f 3 (0f щ' o COS9 о -[sin²9 о +B/AcOS9 о (COS9 о -COS9)]                          (12)

щ o COS 0/sin² 0=щ o COS 0 0 -f 2 0 COS 0.

Поскольку                      щ= w/dt=d щ/d9*d9/dt=d y/d0*0',

^=d^/dt=d^/d0*d0/dt=d^/d0*0, то, учитывая (7), запишем уравнения (9) в виде d^/d0=f 2(0)/f 1(0), d^/d0=f3(9)/f1(9) .                                    (13)

Отсюда, разделяя переменные и используя начальные условия (3) щ^щ^щ о (Со РП о РО. находим

0 f(9^

щ ^ ) = щ ( о ) + f —^-d⁰ ,

0 о ^f 1 ( 0 )

^ ( 0 )

= f

0 о

f 3 ( 0 ) f ( ( 0 )

формулы (11), (14) решают поставленную задачу.

Анализ решения . Из решения выражений (11) и (14) при 0 = п2 , когда дерево легло на грунт, находим время падения дерева:

t

II

п /2 f 0 о

d0

f 1 ( 0 )

а из первого выражения формулы (11) находим угол отклонения ствола от направления надвигания:

п /2 f що = щ/2 = що + f -J0 d0 . 0о f 1(0 )

На рисунке 4 представлена схема расположения упавшего дерева.

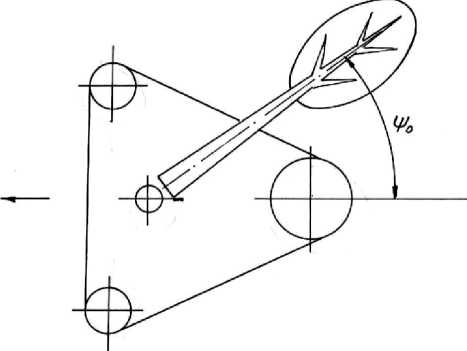
Рис. 4. Схема расположения упавшего дерева относительно ГПЦ

Пример определения времени падения дерева на грунт ( tп ) и угла отклонения фактической плоскости падения от геометрической ( ψ 0 ). Воспользуемся формулами (15) и (16) для вычисления конкретных величин – времени падения дерева на грунт и угла отклонения фактической плоскости падения от геометрической. Для этого зададимся конкретными данными.

Исходные данные. Высота дерева h = 25 м. Диаметр дерева в месте среза D = 0,6 м. Расстояние от места среза до центра тяжести дерева a = 0,38h = 9,5 м. Диаметр кольцевых резцов ГПЦ – Dл = 0,03 м. Масса дерева m = 3500 кг. Момент инерции дерева А = 0,21mJ² = 4,594 х 10⁵ кГ/м². Момент инерции дерева относительно оси вращения В = 200000 кГ/м². G = 9,81м/с². I = 0…n = 0 – 10 – количество точек для вычисления характера кривой. При этих данных характер кривых представлен на рис. 5–6.

t п , с

5
4
3
2
1

0                                                          Θ = π /2

Рис. 5. Кривая времени падения дерева на грунт

ψ 0 , град

50
40
30
20
10

0                                                          Θ = π /2

Рис. 6. Кривая угла отклонения фактической плоскости падения от геометрической

Выводы

• 1.    Процесс валки дерева ГПЦ отличается от традиционных способов спиливания растущего дерева тем, что падающее дерево совершает более сложное движение в пространстве с некоторым вращением и отклонением фактической плоскости падения от геометрической.

• 2.    Процесс падения дерева в многомерном пространстве можно описать с помощью уравнений Лагранжа-Пуассона.

• 3.    Найдены выражения для определения времени падения дерева на грунт и угла отклонения ствола от направления надвигания.