Теоретические основы расчета системы управления гидравлического привода стенда для испытаний поршневых гидравлических цилиндров

Introduction. The durability and performance of hydraulic machines is determined through life tests. At that, various braking devices (mechanical, electric, hydraulic, etc.) are used for strength loading of the hydraulic motor, as a result of which a significant amount of energy is lost. This can be avoided if the method of rotational motion with energy recovery is used during life tests. This approach is applicable for hydraulic pumps, motors, and hydraulic cylinders.

Materials and Methods. A test bench is presented, the design of which provides recreation of the conditions most appropriate for the field operation of hydraulic cylinders. In this case, energy recovery is possible. To solve the research problems, methods of mathematical modeling were used, the basic functional parameters of the proposed design were calculated. The determination of the pressure increment at various points in the hydraulic system is based on the theory of volumetric rigidity. When modeling the motion of the moving elements of the bench hydraulic system, the laws of rotor motion are used. Research Results. In the structure of the test bench, the cylinders in question are located in the pressure main between the hydraulic pump and the hydraulic motor. This enables to significantly reduce the bench itself and to save a significant amount of energy due to its recovery. A basic hydraulic diagram of the test bench for piston hydraulic cylinders is presented, in which the operation of the moving elements of the system is shown. A mathematical modeling of the hydraulic system of the bench is performed. A kinematic diagram of the mechanism for transmitting motion between test cylinders is shown.

Discussion and Conclusions. The system of equations presented in the paper shows how the increment of pressure at the selected nodal points of the energy recovery system is determined (in particular, how the increment depends on time, re-

зависит от времени, приведенного коэффициента объем-      duced coefficient of volumetric rigidity, operating fluid con- ной жесткости, расхода рабочей жидкости, площади      sumption, and piston areas). The velocities of the hydraulic поршней). Величины скоростей перемещения плунжеров pistons are determined according to the kinematic scheme of гидравлических цилиндров определены согласно кинема- the mechanical transmission of the bench. Thus it can be ar-тической схеме механической передачи стенда. Итоги исследования позволяют утверждать, что, благодаря пред-      gued that, thanks to the solution presented in the paper, the life ставленному в статье решению, результаты ресурсных      test results of hydraulic cylinders will adequately reflect their испытаний гидравлических цилиндров будут адекватно      operation under rated duties.

отражать их работу при номи нальном режиме эксплуатации.

ния.

Образец для цитирования: Теоретические основы расче- For citation: A.T. Rybak, et al. Theoretical background of та системы управления гидравлического привода стенда      hydraulic drive control system analysis for testing piston для испытаний поршневых гидравлических цилиндров /      hydraulic cylinders. Vestnik of DSTU, 2019, vol. 19, no. 3,

А. Т. Рыбак [и др.] // Вестник Дон. гос. техн. ун-та. — pp. 242-249. — Т. 19, № 3. — С. 242-249.      242-249

10.23947/1992-5980-2019-19-3-242-249

Введение. Одним из важных этапов машиностроительного производства, в том числе и производства гидравлических машин, является испытание конечного продукта на соответствие техническим требованиям [1].

Наиболее     значимые     (при     этом     трудо-     и     энергозатратные)     испытания

— ресурсные. Они позволяют определить долговечность, работоспособность оборудования в процессе длительного применения по назначению. Ресурсные испытания следует проводить в режиме, максимально приближенном к номинальному режиму эксплуатации гидравлических цилиндров. При этом для силового нагружения гидравлического двигателя применяются различные тормозные устройства (механические, электрические, гидравлические и другие), в результате чего теряется значительное количество энергии, переходящей в тепло. Особенно это касается испытаний гидравлических машин средней и высокой мощности.

В результате активных поисков решения обозначенной проблемы разработан метод ресурсных испытаний гидравлических машин вращательного движения с рекуперацией энергии [2–4]. Такой подход дает значительную экономию при испытаниях гидравлических насосов и гидравлических моторов. Для гидравлических цилиндров также разработаны способы испытаний с рекуперацией энергии [5–10]. Схемы, описанные в [9, 10], позволяют изготовить стенд, обеспечивающий полное соответствие режима функционирования гидроцилиндров их работе в реальных условиях эксплуатации.

Материалы и методы

Постановка задачи. Предложена конструкция стенда, которая позволяет в ходе испытаний воссоздать условия, максимально соответствующие реальной эксплуатации гидроцилиндров. При этом возможна рекуперация энергии, что значительно снижает ее затраты, особенно при ресурсных испытаниях. Для решения задач исследования использованы методы математического моделирования, рассчитаны основные функциональные параметры предлагаемой конструкции.

Машиностроение и машиноведение

Описание испытательного стенда. Стенд для ресурсных испытаний поршневых гидроцилиндров с рекуперацией энергии разрабатывался на основе ранее предложенного метода испытаний с рекуперацией энергии объемных гидравлических машин вращательного действия [3, 4]. Данное решение подразумевает, что гидравлический мотор через систему механического привода возвращает энергию на вал гидравлического насоса. Испытываемые гидроцилиндры размещаются в напорной магистрали между гидронасосом и гидромотором [5, 6]. Такие испытания позволяют существенно уменьшить сам стенд и сэкономить значительное количество энергии за счет ее рекуперации.

Принципиальная гидравлическая схема стенда для испытаний поршневых гидроцилиндров изображена на рис. 1.

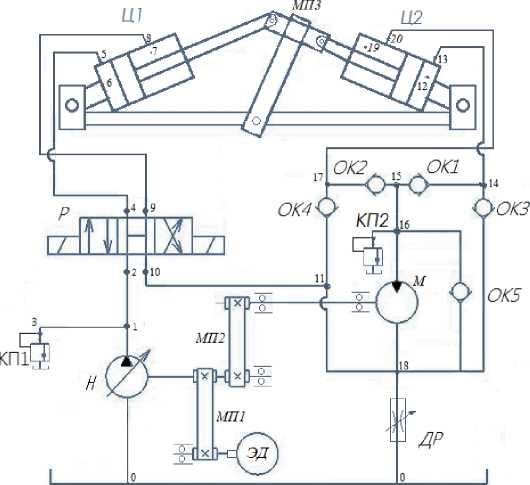
Рис. 1. Принципиальная гидравлическая схема стенда для ресурсных испытаний поршневых гидроцилиндров с рекуперацией энергии

На рис. 1 показано, что в напорную гидролинию между гидронасосом и гидромотором устанавливаются испытываемые гидравлические цилиндры Ц1 и Ц2, связанные между собой механической передачей МП3.

Стенд функционирует следующим образом. Электрический двигатель ЭД посредством механической передачи МП1 приводит во вращение вал гидравлического насоса Н. Энергия, сообщаемая при этом рабочей жидкости, переносится ею по гидролинии 1–2 на вход гидравлического распределителя Р, который направляет ее, например, по магистрали 4–5–6 в поршневую полость гидравлического цилиндра Ц1.

Гидроцилиндр Ц1 посредством механической передачи МП3 передает полученную от рабочей жидкости энергию на шток гидравлического цилиндра Ц2, который в этом случае выполняет функцию насоса и передает энергию рабочей жидкости, находящейся в его поршневой полости.

Из поршневой полости гидроцилиндра Ц2 рабочая жидкость по гидролинии 12–13–14–15–16 подается на вход гидравлического мотора М, который преобразует полученную от рабочей жидкости энергию в энергию вращения вала. Вращение вала гидромотора М посредством механической передачи МП2 передается на вал гидронасоса Н. Передача МП2 рассчитана таким образом, что частота вращения, передаваемая на вал гидронасоса Н от вала гидромотора М, несколько выше той частоты, с которой первичный источник энергии (электродвигатель ЭД) вращает вал гидронасоса. Это способствует затормаживанию вращения вала гидромотора М. Как следствие, повышается давление на входе и открывается предохранительный клапан КП2. Давление возрастает также в гидроцилиндрах Ц1 и Ц2, что обусловливает их работу в соответствующем режиме.

Когда шток гидроцилиндра Ц1 выдвигается на полный ход, на распределитель Р подается команда о смене позиции — и рабочая жидкость, поступающая на вход распределителя Р от гидронасоса Н, направляется по гидролинии 9–8–7 в штоковую полость гидроцилиндра Ц1. Это вызывает обратное движение его поршня, но система рекуперации энергии функционирует, как и при прямом ходе поршня.

Результаты исследования

Математическое моделирование гидравлической системы стенда. Разработаем математическую модель предлагаемой рекуперативной системы испытаний поршневых гидравлических цилиндров. В качестве основы используем теорию объемной жесткости [11–13] с учетом приведенных коэффициентов объемной жесткости гидравлических элементов. Такой подход позволяет более точно моделировать систему, приближенную к реальным условиям эксплуатации гидроцилиндров [14–19]. Особое внимание при моделировании гидравлических приводов следует уделять определению приведенного коэффициента объемной жесткости гидравлических магистралей. Его величина для металлических трубопроводов рассчитывается по известным зависимостям, а для рукавов высокого давления (РВД) определяется экспериментально [20, 21].

В соответствии с теорией объемной жесткости уравнение приращения давления в любой точке гидравлической системы может быть определено по уравнению dp = ct(£ 0- Y'Q- Ь-, где E Qbxi и E Qbmxi — суммарные входящие и выходящие из рассматриваемого (i-го) объема системы расходы рабочей жидкости за время dt; С — приведенный коэффициент объемной жесткости выбранной области гидросистемы.

Условно разделим гидравлическую систему стенда (рис. 1) узловыми точками. Примем как точку 0 объем гидравлического бака с давлением, равным атмосферному, и запишем уравнения для определения давления в выбранных узловых точках.

dp1 = С1( Он — 01-2 - 01-д)К, dp2 = С2(01-2-02-4 W , dp3 = Сз(01-з-0кп1 )dt, dP4= C4(Q2-4-Q4-5 )lt , dp5 = C5(Q4-5 - Q5-6 )dt, lP6 = CH1(Q5-6 -Wn)dt , dp7 = Сшт1(^п1./п.шт — Q7-8 )dt , dp8= С8(07-8— Q8-9)dt , dp9= С9(08-9— Q9-10)dt , dp10 = С10(09-10 — Q10-11)dt , dp11 = С11(010-11 — Q11-18 — Q0K4)dt , dp17 = С17(0ОК4 — Q17-20 — QOK2)dt , dp20 = С20(017-20 — Q20-19)dt , dp19 = Сшт2(020-19 — Wn^dt , dp12 = Сп2(Рп2/п — 012-13 )dt , dp13 = С13(012-13    Q13-14)dt , dp14 = С14(013-14 + QOK3 — QOK1)dt , dp15 = С15(0ОК1 + QOK2 — Q15-16 )dt , dp16 = С16(015-16 + 0ок5 — 0КП2 — Qm )dt, dp18 = С18(0

11-18

+ QM

—

⁰ДР ^{— Q}OK3 ^{— Q}OKS^)dt -

Здесь dp 1 …dp 5 — приращения давления в характерных точках напорной гидролинии цилиндра Ц1 за время dt ; dp 7 …dp 10 — приращения давления в характерных точках сливной гидролинии цилиндра Ц1 за время dt ; dp 11 …dp 18 — приращения давления в характерных точках гидравлической системы рекуперации энергии, включающей гидроцилиндр Ц2 и гидромотор М, за время dt ; dp 6 и dp 7 — приращения давления в поршневой и штоковой полостях гидроцилиндра Ц1 за время dt ; dp 12 и dp 19 — приращения давления в поршневой и штоковой полостях гидроцилиндра Ц2 за время dt ; dp 20 — приращение давления на выходе из штоковой полости гидроцилиндра Ц2 за время dt ; C 1 … C 5 , C 8 … C 11 , C 13 … C 18 и C 20 — приведенные коэффициенты объемной жесткости в характерных точках гидравлической системы стенда; C _п1 и C _п2 — приведенные коэффициенты объемной жесткости поршневых полостей гидравлических цилиндров Ц1 и Ц2 [11–13]; C _шт1 и C _шт2 — приведенные коэффициенты объемной жесткости штоковых полостей гидравлических цилиндров Ц1 и Ц2 [11–13]; Q _Н — производительность гидравлического насоса Н; Q _М — расход рабочей жидкости через гидравлический мотор М; Q _ОК1… Q _ОК5 — расходы рабочей жидкости через обратные клапаны ОК1…ОК5; Q _КП1 и Q _КП2 — расходы рабочей жидкости через предохранительные клапаны КП1 и КП2; Q 1_3 , Q 1_2 , Q 2_4 , Q 4_5 , Q 5_6 , Q 7_8 , Q 8_9 , Q 9_10 , Q 10_11 , Q 11_18 , Q ₁₉ _ ₂₀, Q 1314 — расходы жидкости на соответствующих участках гидравлической системы стенда; г_п1 и г_п2 — скорости движения поршней гидроцилиндров Ц1 и Ц2 соответственно; f п — площади поршней испытываемых гидравлических цилиндров Ц1 и Ц2; f _п.шт — площади поршней испытываемых гидравлических цилиндров Ц1 и Ц2 со стороны штоковых полостей.

Машиностроение и машиноведение

Значения расходов рабочей жидкости, необходимые для расчета приращения давлений, определяются по формуле:

^Oi = ^Ц^

—

р +1 1 • sign(P i

—

P i+1 ⁾ .

Здесь P i и p_i+1 — величины давлений на входе и выходе гидравлических сопротивлений; f — площадь живого сечения соответствующего сопротивления; ц — коэффициент расхода сопротивления; р — плотность жидкости.

Для участков гидравлических линий (линейных гидравлических сопротивлений) приведенный коэффициент расхода определяется по формуле:

H = H i =

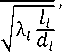
где dl и ll — внутренний диаметр и длина соответствующего участка трубопровода; X _l — величина коэффициента гидравлического трения участка трубопровода, определяемая с учетом режима течения рабочей жидкости и свойств трубопровода.

Приведенные коэффициенты объемной жесткости металлических трубопроводов определяются по формуле [11-13]:

• с - ⁴ _Eil_

• ⁴    nd²i , , d^E/Z ^,

• 6 Ei

где d и l — диаметр рассматриваемого трубопровода и его длина; 5 — толщина стенки трубы; Ef _l и E_l — величины модуля упругости жидкости и материала стенки трубопровода.

Величину приведенного коэффициента объемной жесткости РВД и трубопроводов, изготовленных из упругих материалов, необходимо определять экспериментально [20, 21].

Производительность насоса определяется с учетом его объемного коэффициента полезного действия

_А     <7н ^ н

Он = ""5 Ло , 2п где qН — рабочий объем гидронасоса; юН — частота вращения вала гидронасоса; п0 — величина мгновенного значения объемного КПД насоса.

_ 1               Л рн

.

Л о = ^{1 — (1 —} Л о.пот ) • ~--- ^р пот

Моделирование движения подвижных элементов гидравлической системы стенда. Величины рабочих зазоров обратных клапанов определяются из уравнения движения их затворов:

dvK„ 1 кл dt   т„л кл где vкл — скорость перемещения затвора клапана; mкл — приведенная масса затвора клапана; hкл — перемещение (величина рабочего зазора) затвора клапана; dкл — диаметр отверстия клапана; Fпр — сила воздействия

I 4 ^{(Р 1} кл

—

^р2кл )    ^Рпр ],

d^KTT кл

""dT = ^{У кл} ’

пружины на затвор клапана; t — время.

Закон движения роторов гидронасоса Н и гидромотора М описывается уравнением их движения:

dMM   1г   ,

^{— р}2М ) ^{— M}M^] -

,.  = ,  [WM(p1M dt    J M dwH dt

= T" ⁽ М эд 1 мп1 + М_м1 мп2 ^— № н^(р1 ^{— р}ат )). ^JP

Здесь wМ, wН — характерные объемы мотора М и насоса Н соответственно; wM и мН — угловые скорости вра щения валов гидромотора М и насоса Н; 1Н, JM — центральные моменты инерции роторов гидронасоса и гидромотора; p 1М — давление на входе гидравлического мотора М; p2М — давление на выходе гидромотора М; pат — давление на входе насоса Н (давление в баке, принимается равным атмосферному давлению); p1 — давление на выходе гидравлического насоса Н; MЭд и MM — крутящие моменты, создаваемые электродвигателем и гидро- мотором соответственно; iМП1 и iМП2 — передаточные отношения механических передач МП2 (от вала гидромотора на вал гидронасоса Н) и МП1 (от вала электрического двигателя на вал гидронасоса Н) соответственно.

Механическая передача МП2 обеспечивает соотношение скоростей вращения валов гидромотора М и гидронасоса Н, описываемое формулой:

^Mm = ш_н1_МП 2 .

Моделирование механической схемы стенда. Для определения величин скоростей перемещения плунжеров гидравлических цилиндров рассмотрим кинематическую схему механической передачи стенда МП3 (рис. 2).

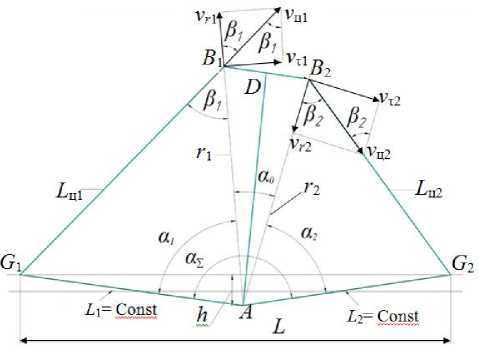
Рис. 2. Кинематическая схема механизма передачи движения между испытуемыми цилиндрами

Передача работает следующим образом. Корпуса гидроцилиндров Ц1 ( L ц1 ) и Ц2 ( L ц2 ) шарнирно крепятся соответственно в точках G 1 и G 2, а их плунжеры шарнирно соединяются в точках B 1 и B 2 с коромыслом, имеющим ось вращения в точке А.

Допустим, что ведущий гидроцилиндр (гидравлический двигатель) является гидроцилиндром L ц1 , а рабочий цилиндр (гидравлический насос) является гидроцилиндром L _ц2. Скорость плунжера гидроцилиндра L _ц1 устанавливается соответственно расходу Q 5_6 рабочей жидкости, поступающей в его поршневую полость. Тогда скорость движения его плунжера можно определить по формуле

^Q s 6 ^vm = -Г". 7 п

Движение плунжера гидроцилиндра L Ц ₁ через шарнир B 1 передается на коромысло AD , которое вращается вокруг точки A. Разложив скорость соединения B 1 на радиальную v_r1 и тангенциальную v_T1, определим значение тангенциальной составляющей:

• У т1 = У ц1 • SinP i .

Тогда угловую скорость ω AD вращения коромысла AD можно определить из выражения

_ Vt1

^Mad —    ,

' 1

где r 1 — длина радиуса, соединяющего точку A вращения коромысла с шарниром B 1 .

Через коромысло AD движение плунжера гидроцилиндра L_ц 1 передается плунжеру гидроцилиндра L _ц2, связанного с коромыслом AD посредством шарнира B 2 . В этом случае тангенциальную скорость шарнира B 2 определим по формуле:

• ^VT2 ^{— Г}2 ^Ш АП ,

где r 2 — длина радиуса, соединяющего точку A вращения коромысла с шарниром B 2 .

Спроецировав величину тангенциальной скорости движения шарнира B 2 на направление перемещения плунжера гидроцилиндра L ц2 , определим скорость его перемещения

V t2

• ^{У ц} 2 = Sm0 2 .

Величины углов β1 и β2 определятся по закону косинусов из треугольников AG1B1 и AG2B2 соответ- ственно:

CosP 1 —

Cos₽ 2 —

1 ^{2        2} __ 7 2

Ь ц1 + ' 1 Ь 1

2Ь ц1 ' 1

Т ^{2       2} — Г ²

^ьц2 + ' 2 ^ь2

2^ ц2^Г2

Машиностроение и машиноведение

Здесь L_ц1 и Ь_ц2 — расстояния между осями крепления соответствующих гидроцилиндров к раме стенда и к коромыслу с учетом степени выдвижения их плунжеров; L 1 и L 2 — расстояния между осью вращения коромысла и точками крепления к раме стенда шарниров корпусов гидравлических цилиндров.

Обсуждение и заключения . Представленная в статье система уравнений показывает, каким образом определяется приращение давления в выбранных узловых точках системы рекуперации энергии (в частности, как приращение зависит от времени, приведенного коэффициента объемной жесткости, расхода рабочей жидкости, площади поршней). Величины скоростей перемещения плунжеров гидравлических цилиндров определены согласно кинематической схеме механической передачи стенда. Итоги исследования позволяют утверждать, что, благодаря представленному в статье решению, результаты ресурсных испытаний гидравлических цилиндров будут адекватно отражать их работу при номинальном режиме эксплуатации.