Теоретические основы создания малогабаритного силового оборудования и механизмов различного назначения с реверсивным термомеханизмом (РТМ) из сплава с памятью формы

В настоящее время всё более широкое практическое применение находят силовые и управляющие элементы из сплавов, обладающих эффектом памяти формы [1]. Известно, что данный эффект основан на фазовом термоупругом мартенситном превращении. Такие сплавы способны при нагреве самопроизвольно принимать одну форму, а при охлаждении другую, производя при этом работу против внешних напряжений, достигающих 600 МПа [2]. Широкие перспективы применения сплавов с памятью формы открываются при разработке оборудования, позволяющего стабильно воспроизводить перемещения, деформации и усилия. Одно из условий многоразовой работы таких устройств – термоупругость прямого и обратного превращения в материале силового элемента. Термоупругость эквивалентна требованию, согласно которому напряжения, наводимые в объёме материала, не должны превышать предела его текучести.

В статье изложены результаты исследования распределений напряжений и температур в цилиндрическом РТМ, возникающих при протекании в его объёме термоупругого мартенситного превращения.

учётом зависимости параметров материала от температуры. В силу осевой симметрии в этой области макродеформация, макронапряжения, температурное поле и параметры материала будут функциями только координаты r вдоль радиуса цилиндра и времени t . Известно [3, 4], что при термоупругом мартенситном превращении сохраняется когерентность границы образующихся фаз, а это позволяет проводить расчёт напряжений в рамках теории упругости. Таким образом, рассмотренная физическая постановка задачи эквивалентна математической модели для осесимметричной задачи термоупругости с параметрами материала, зависящими от координаты r и времени t [5].

Математическая модель поставленной задачи в цилиндрической системе координат будет состоять из уравнения равновесия r -   + °г -°9 = 0,(1)

уравнений совместности деформаций r . ^Ее-Е = 0,

Е d r

= 0

.

и соотношений Коши duи

Е = — Е = — Е = —С4')

r , е , z ,х*)

dr      r где и и to - радиальная и осевая компоненты вектора перемещений; е r, Ее , е z - радиальная, тангенциальная и осевая компоненты тензора деформаций; a r и (Ге - радиальная и тангенциальная компоненты тензора напряжений.

Компоненты тензоров деформаций и напряжений связаны соотношениями [3]:

Er = -1 °v°o0 +°z)]+p,(5)

E

Ee = -1 \°.^z -°.)] + p,(6)

E

Ez =  °^r + oe)] + p.(7)

E где E(r,t) и v (r,t) - модуль Юнга и коэффициент Пуассона; P = E Т+ 5 — сумма температурной и структурной деформаций, о Z - осевая компонента тензора напряжений.

Полученная система уравнений (1)–(7) была решена при следующих граничных условиях:

на боковой поверхности цилиндрического РТМ

где О С =

P

^ R ²

B P

b5 (R)-b2 (R )Ьз (R) b1( R)

b 4 ( R ) - b 2 ( R )

B = 2------ b1 (R) '

b 3 ( r ) = ^T r ( 1 + 2 V 1 ( ^ )) P ( ^ ) ^ d ; , r ₀

R b, (R) = -2 J E1(^X

R ₀

О = ^0(r = R ,        (8)

на торцах цилиндрического РТМ

R

Р = 2 ^ J a_zrdr .          (9)

bU\= — f        ^{1 + 2 v} 1 ⁽ ^^

b ^{5 (} r ⁾ R J ^^{P (} ^ ⁾ E ^{1 (} ^ ^} 7+ VM d ^ ,

О- ^{( r )} =

E 1 ( r )

1 + V 1 ( r ) L‘

^b 2 ^{( R ) b} 1 ^{( R )} ₊ ^b 3 ^{( R )} b ^{( R )} __b (J

_^E 0 ⁽ R ⁾ b ^{2 (} r ⁾      b 1 ( R ) ⁺ b 1 ( R )      b ^{3 (} r ⁾ J , ⁽¹²⁾

Решая краевую задачу термоупругости (1)– (7) с граничными условиями (8) и (9), получаем зависимости (10)–(13) для определения распределения напряжений по сечению РТМ:

^O Z = ^E 0

-V (r) byR + Е (r) + bl(R)        J

+ P   a2 (R) _ 0(r \E о1 + 2v1(r)

^{1 (} r ⁾ a 1 ( R ) ^{P ( r )} E ^{1 ( r )} 1 + v 1 ( r ) ^.

v                  , где V =-----, E. = Е • (1 - V2),

¹ 1 - v ¹

b1(r ) =

^{1 + V} 1 ^{( r )} E 1 ( r )

_L r ^{1 + V 1} Щ yr r ^{2 J} E 1 ( i )

r

b2 (r ) = — /vEE?

r ₀

£ - координата вдоль радиуса РТМ, а₁ ( R ) и а₂ ( R ) – константы интегрирования. Используя граничное условие (9), находим

О ( r ) = - О ( r ) + О ( r ) - E ( R ) bTrx + E ⁽ r ^ + bR

^0V ' ^ZV) 0 b 1 ( R ) 1 + v 1 ( r ) J b 1 ( R ) . ⁽¹³⁾

Подставив (11) в (10), (12) и (13), получим окончательные соотношения, позволяющее рассчитывать распределение осевых, радиальных и тангециальных напряжений при заданных зависимостях E 1 ( r ), V 1 ( r ) и в( r ).

Для нахождения распределения напряжений были проведены экспериментальные исследования по определению E , v и P .

Коэффициенты линейного расширения измерялись на дилатометре. Модуль Юнга определялся динамическим резонансным методом по методике [6]. Методика измерения н изложена также в [6].

Результаты проведённых экспериментальных исследований представлены на рис. 1 и рис. 2. Значения коэффициентов линейного расширения определены экспериментально и составили 14,2·10-6 и 6,1·10-6 К-1 для высоко- и низкотемпературной фаз материала соответственно.

Расчёт напряжений, возникающих в РТМ, производился следующим образом. Рассчитывалось распределение температуры по сечению цилиндра на основании результатов работы [5]. Например, для случая нагрева силового элемента через боковую поверхность распределение температуры имеет вид:

^E 0

^О С ⁺ B P

B

,

qR

Т = Т +— ⁰ л

2at 1 ( r 2 ²

—2--- 1 - 2”

R ²   4 ( R ² J

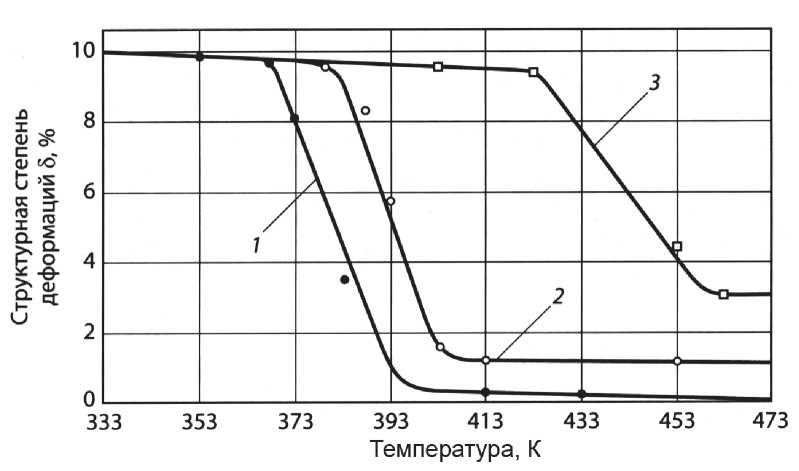
Рис. 1. Структурная деформация образца РТМ в зависимости

от температуры нагрева и напряжений ст с :

1 - ст с =0;  2 - СТ =100 МПа; 3 - СТ =300 МПа

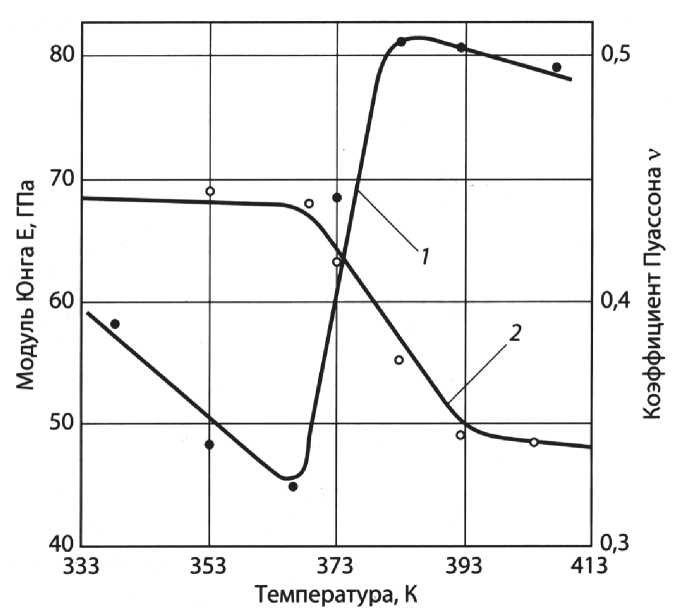
Рис. 2. Изменение модуля Юнга (1) и коэффициента Пуассона (2) образца РТМ из сплава TH-1 в зависимости от температуры нагрева К

где Т ₀ – начальная температура образца, q – плотность теплового потока на поверхности образца, X и а — коэффициенты теплопроводности и температуропроводности соответственно, t – время нагрева.

По соотношению (14) и экспериментальным зависимостям (рис. 1 и 2) определялось распределение упругих постоянных по сечению цилиндра, а их полученные значения использовались для численного интегрирования по соотношениям (10)–(13). В расчётах область интегрирования разбивалась на 30 точек.

Результаты расчёта интенсивности напряжений ст i ( r ) возникающих в РТМ для различных по величине рабочих напряжений ус представлены на рис. 3. Распределение интенсивности напряжений соответствует моменту времени, при котором температура в точке r =0,2 R равна тем-

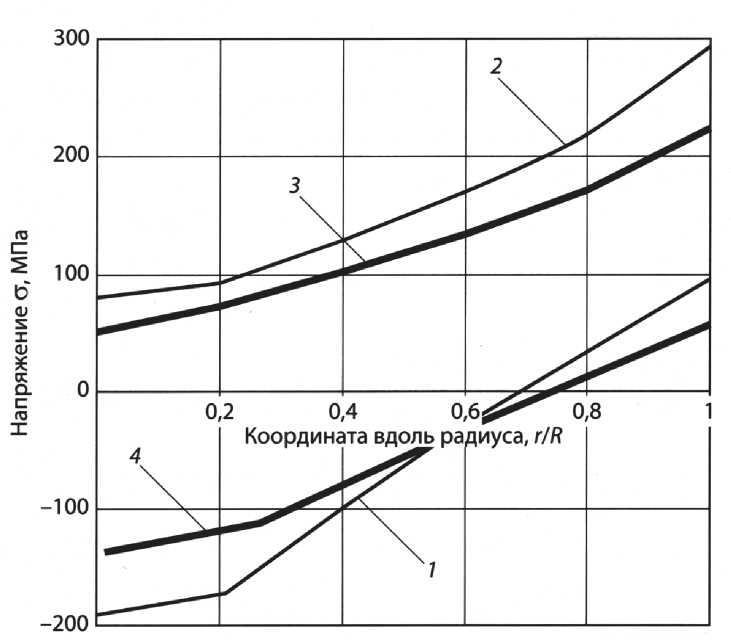
Рис. 3. Распределение интенсивности напряжений по радиусу РТМ в зависимости от внешних растягивающих (1, 2) и сжимающих (3, 4) напряжений о :

1 - о с =0; 2 - о с =200 МПа; 3 - о с =0; 4 - о =200 МПа

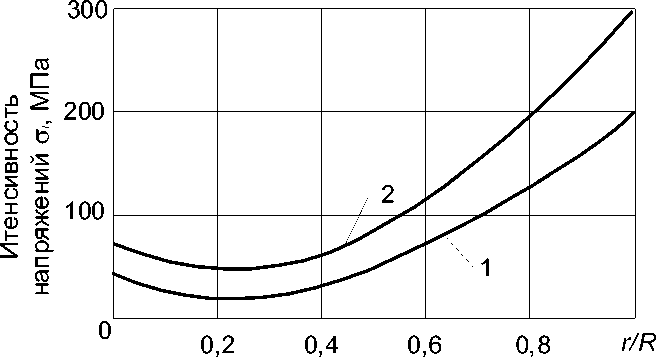
Рис. 4. Распределение напряжений по радиусу РТМ при нагреве в момент времени t = 10 с ( о _c=200 МПа): 1 - тангенциальные напряжения у_и, 2 - осевые напряжения о

пературе начала обратного мартенситного превращения, а температура поверхности РТМ больше этого значения на два градуса.

Исследования показали (рис. 3, 4), что при обратном мартенситном превращении в зависимости от диаметра РТМ, температурного градиента по его сечению и внешних растягивающих или сжимающих рабочих нагрузок интенсивность напряжений в РТМ изменяется в широких пределах и может достигать предела текучести материала ( о Т=320 МПа).

Кроме того, максимальными по абсолютной величине являются осевые напряжения о Z (рис. 4), причём при нагреве их максимальная величина достигается на внешней поверхности, а при охлаждении на внутренней. Поэтому при разработке оборудования для периодического многоразового использования необходимо провести по предложенной методике предварительные расчёты, устанавливающие взаимосвязь геометрических размеров РТМ с

Рис. 5. Силовое оборудование с РТМ из сплава с памятью формы усилием 1000 кН максимальными развиваемыми усилиями и максимальным градиентом температуры по его сечению. Анализ результатов расчёта и экспериментов показал их хорошую сходимость. Предложенная методика была использована для разработки и изготовления оборудования с РТМ из материала с памятью формы ТН-1.

Общий вид силового оборудования - пресса для ремонтно-восстановительных работ усилием 1000 кН представлен на рис. 5, силовой замок-фиксатор – на рис. 6.

Разработанный класс силового ремонтновосстановительного оборудования и механизмов

Рис. 6. Силовой замок-фиксатор существенно меньше по габаритам и весу своих аналогов, значительно меньше потребляет электрической энергии, позволяет осуществить процесс механизации и автоматизации с наименьшими затратами, экономит производственные площади.

Преимущественная область применения данного силового оборудования –разделительные операции на листовых металлических и неметаллических материалах, формообразующие и сборочно-монтажные работы. Применение механизмов- компактные узлы и агрегаты ответственного назначения.