Теоретические основы способа суммирования световых потоков от отдельных источников излучения для наземной отработки космических аппаратов

При проектировании оптических систем, в частности, таких как имитатор солнечного излучения для наземной отработки космических аппаратов, зачастую становится актуальной задача объединения световых потоков, полученных из нескольких (возможно десятков) источников излучения, в единый.

Эта задача возникает при необходимости иметь световое пятно большого размера – 4 м2 и более, а серийно выпускаемых ламп сопоставимой мощности нет ввиду узкой области применения. Здесь возникает вопрос оптимального совмещения геометрии излучения каждого отдельного источника с остальными, чтобы получить такой суммарный поток, который можно было бы рассматривать как единое целое и применять для его преобразования законы оптики.

При этом необходимо решать задачу либо при построении совершенно нового имитатора солнечного излучения, либо при встраивании излучательной системы в уже существующую светооптическую схему.

Проблема суммирования целиком зависит от условий, в которых строится имитатор Солнца и его излучательная система, и требований, предъявляемых к имитатору солнечного излучения. Это, в первую очередь, габаритные условия – площадь для размещения излучательной системы, площадь, на которой нужно «собрать» итоговое световое пятно, и возможные расстояния между этими площадями. Требования заключаются в мощности итогового светового пятна и его спектральном составе. Ограничения, образованные габаритными условиями, и предъявляемые к ИСИ требования определяют постановку задачи суммирования. Несколько усложняет задачу неопределенность, связанная с потерей энергии (возможно и качества) излучения на поверхностях оптических элементов. Поэтому, если речь идет о построении «нового» имитатора Солнца, то задачу суммирования нужно определять, уже предполагая уровень потери мощности потока после этого суммирования, поскольку требования предъявляются, как правило, к световому пятну на испытываемом космическом аппарате. Здесь необходимо предварительно установить, сколько и какие оптические элементы планируется разместить после суммирования.

При встраивании системы излучения в уже существующую схему величина последующих потерь, как правило, известна.

Таким образом, чтобы приступить к расчету схемы суммирования, необходимо заранее определить следующие параметры:

– мощность и площадь сформированного светового пятна;

– мощность и спектральную характеристику одного источника излучения;

– расстояние от источников излучения до сформированного пятна.

Рассмотрим принципиальный подход к построению такой схемы суммирования световых потоков, когда необходимо объединить мощности от нескольких источников излучения на сколь это возможно минимальной площади S (м²), сформировав таким образом сходящийся световой поток, причем расстояние от источников излучения до сформированного пятна тоже должно быть минимальным – L (м) (рис. 1).

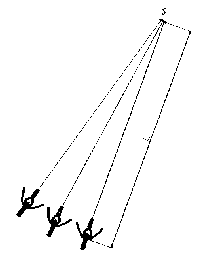
Рис. 1. Условная схема суммирования световых потоков от нескольких источников

При этом на площади S необходимо получить световой поток мощностью Феs [Вт]. Мощность светового потока одного источника излучения обозначим Феi . Тогда количество источников излучения для формирования светового потока требуемой мощности можно вычислить по формуле

N =

Ф _ei ⋅η _i ⋅τ _i

где η i – КПД одного источника излучения; τ i – энергетическая эффективность связки «источник излучения – облучаемая площадка».

КПД источника излучения однозначно определяется подобранным типом источника.

Обоснование подбора типа источника излучения для имитатора Солнца подробно приведено в работе [1].

Энергетическая эффективность связки «источник излучения – облучаемая площадка» зависит от площади поверхности зеркального элемента (рефлектора), собирающего равномерно излучаемые источником во все стороны лучи и направляющего их в нужную зону. Разумеемся, чем больше охватывает рефлектор лампу, тем выше эффективность.

Также при построении схемы суммирования необходимо учесть, что угол, образованный суммой потоков (угол падения), не должен превышать 30°, для того чтобы весь поток прошел границу «воздух– стекло», а не претерпел частичного отражения.

Далее приведем геометрические обоснования для расчета кривых рефлекторов и схемы суммирования.

Для того, чтобы собрать равномерно исходящие от источника лучи в небольшой зоне (идеально – в точке), очень удобно использовать свойства кривой 2-го порядка – эллипса.

Известно, что нормаль и касательная к эллипсу в любой точке М являются биссектрисами, соответственно, внутреннего и внешнего углов, образованных радиусами-векторами, проведенными из фокусов эллипса в эту точку (рис. 2) [2].

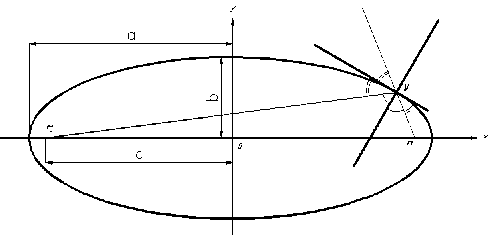
Рис. 2. Нормаль и касательная к эллипсу в точке

Отсюда, если предположить, что точечный источник излучения размещен в первом фокусе эллипса, а внутренняя поверхность эллипса является зеркальной, то любой луч, исходящий из первого фокуса, отразившись от зеркальной поверхности, непременно попадет во второй фокус. Это объясняется из законов отражения (угол падения света равен углу отражения и от кривой свет отражается также, как от касательной, проведенной в точку падения) и теоремы равенства вертикальных углов.

Таким образом, выполнив рефлектор в виде эллипсоида вращения, получим, что весь световой поток от источника излучения, попавший на стенки рефлектора и отразившись от них, соберется во втором фокусе (рис. 3).

Для эффективности рефлектора, выполненного в виде эллипсоида вращения, взаимосвязь между его параметрами – полуосями a и b и расстоянием c существенна (рис. 2):

a ² = b ² + c ².

Это означает, с одной стороны, что чем меньше расстояние от вершины эллипса до первого фокуса (в котором размещен источник излучения), тем большая часть излучения попадет на его поверхность и далее – в требуемую зону. С другой же стороны, это влечет за собой увеличение межфокального расстояния или расстояния от источника до облучаемой площадки (эллипс получается более вытянутый).

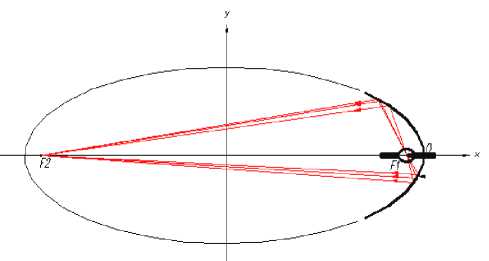
Рис. 3. Рефлектор в виде эллипсоида вращения

Здесь важно для построения схемы суммирования найти «золотую середину». Если обозначить расстояние от вершины рефлектора до первого фокуса OF ₁, а расстояние от вершины до второго фокуса OF ₂, то задав числовое значение OF 2 и изменяя в допустимых пределах OF 1 , можно составить множество систем уравнений типа:

OF 1 = a - c ;

OF 2 = a + c .

Тогда, используя вышеприведенную связь параметров, нетрудно определить все характеристики возможных эллипсоидов-рефлекторов. Оптимальным будет являться тот эллипсоид, площадь поверхности которого при равных наружных диаметрах больше.

Площадь поверхности эллипсоида однозначно определяется длиной дуги эллипса, которая является образующей данного эллипсоида. Ее можно вычислить по формуле

t2

l = a j 71 - e 2 cos ² tdt, t ₁

2    7 2

• 2 a - b

где e =--- 2— - квадрат эксцентриситета эллипса;

a ²

t = arctan(фk ■ tan ф) - эксцентрический угол; ф - п a угол точки на эллипсе, здесь ф е (0,—),к = —.

2 b

Далее, на основе известного количества источников излучения и оптимальных параметров одного рефлектора-эллипсоида уже можно сформировать схему суммирования потоков. Для этого, задав наружный диаметр одного рефлектора и зная расстояние OF2, получим телесный угол светового потока одного источника излучения. Очевидно, что совместив вторые фокусы F2 всех рефлекторов в одну точку, получим некоторый «суммарный» поток, мощность которого в этой точке будет равна сумме мощностей потоков отдельных рефлекторов. При этом вершины всех рефлекторов будут располагаться на поверхности сферы с центром в точке совмещения вторых фокусов рефлекторов. Способ размещения рефлекторов относительно друг друга определяет требование компактности в конструкторском решении построения системы излучения и минимально возможный телесный угол «суммарного» потока.

Возможные построения схем суммирования световых потоков от 7 и 10 источников излучения показаны на рис. 4.

Со схемой суммирования (см. рис. 4) можно работать, как со световым потоком от одного источника излучения с углом сходимости, определенным «крайними» позициями рефлекторов. Понятно, что суммарный поток не будет иметь «четкой» конусообразной формы, но это будет некая его часть – «вырезка». Пример преобразования такого суммарного потока двояковогнутой линзой в параллельный показан на рис. 5.

Для определения углов наклонов отдельных рефлекторов в составе схемы суммирования рассмотрим треугольник OOiF 2 и его проекции на плоскости YOZ и XOZ (рис. 6).

Здесь O_i F 2 – расстояние от вершины i -го рефлектора до второго фокуса всех рефлекторов, а x_i и y_i – координаты i -го рефлектора. Углы наклона рефлектора по x и y можно определить из проекций треугольника OOiF2 на плоскости YOZ и XOZ . Это углы Lx и Ly соответственно. Угол Lx равен углу OyiF2O как вертикальный. Аналогично угол Ly равен углу OxiF2O . Обозначив O_i F 2 за f , имеем

y

Sin Lx = :-------- 7,

OyiF 2

где

I OyiF 2| = V f 2 - x,² , откуда

()

Lx = arcsin —,

l

Аналогично sin Ly=iOxiF^ -OxF2=^f2 - yi2,

Рис. 4. Схемы суммирования световых потоков для 7 и 10 источников излучения: а – 7 источников излучения; б – 10 источников излучения

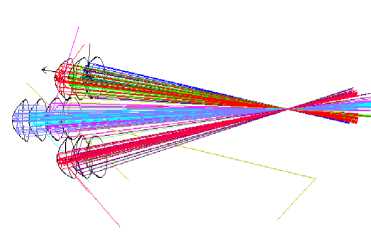
б

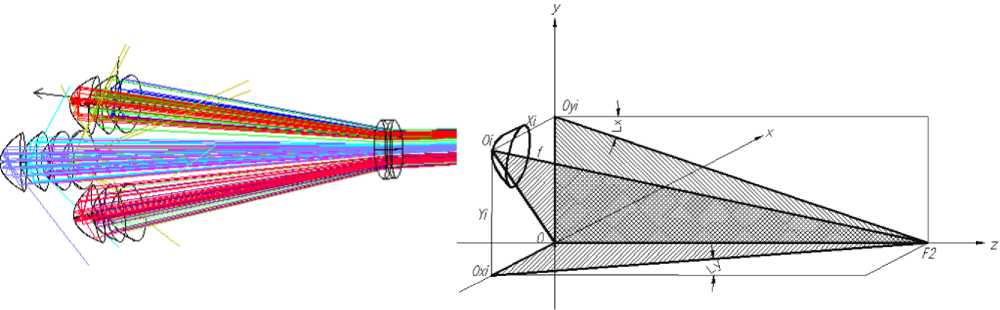
Рис. 5. Преобразование суммарного светового потока в параллельный

Рис. 6. Определение углов наклонов рефлекторов

Ly = arcsin

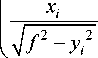
Все изложенное идеально справедливо лишь для точечных источников излучения. Но в реальной практике источники имеют конечные размеры. Для предложенных в работе [1] ксеноновых ламп OSRAM «точечный источник излучения» – это конусообразная дуга длиной в 13 мм. Здесь возникает вопрос об отклонениях лучей светового потока в силу этого отличия, и должен быть проведен дальнейший расчет с учетом возможных отклонений. Современные компьютерные программы для оптических расчетов позволяют с достаточной точностью вводить такие параметры источника излучения, как форма дуги и пространственное распространение потока. В результате, расчетные модели, как правило, подтверждаются на практике.