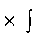Теоретические основы технологии дифференцированного электрообогрева производственных помещений. Математическая модель

Идея дифференцированного (избирательного) обогрева производственных помещений электронагревательными приборами направленного действия, обеспечивающими комфортный, достаточно высокий температурный режим только в зоне рабочих мест при предельно низкой температуре в остальной части помещения открывает перспективу существенной экономии расходов на обогрев помещений в сравнении с традиционной системой пароводяного ото-пления.[1]

Основные понятия и определения, а также совокупность задач, подлежащих решению в процессе разработки данной технологии, подробно изложены в работе [2].

Центральной при этом является задача расчёта интенсивности обогрева объёма рабочего места (ОРМ), т.е. определение величины греющего теплового потока Qг при заданной мощности P электронагревателя и выбранной дистанции обогрева h. Аналитическое ре- шение этой задачи возможно при выполнении ряда основополагающих условий, сформулированных в работе [2]. Это:

Замена реальной структуры ОРМ и конструкции электронагревателя адекватными моделями, поддающимися математическому анализу;

Обеспечение нормальной пространственной ориентации нагревателя и лучеприемника ОРМ, обеспечивающей минимум потерь лучистой энергии в процессе обогрева.

В итоге проблема сводится к расчёту теплопередачи от высокотемпературной плоскости S 1 модельного излучателя к нормально ориентированной к S 1 низкотемпературной плоскости S 2 лучеприемника модельного ОРМ (см. рис. 1). Для решения задачи плоскости S 1 и S 2 целесообразно разместить в ортогональной системе координат, как это показано на рис. 2.

Рисунок! Схема нормальной пространственной ориентации плоскостей излучателя и лучеприёмника:

1 – плоскость излучателя S 1 ; 2 – плоскость лучеприёмника S 2 ;3 – линия центров, нормальная к обеим плоскостям; 4 – ОРМ; 5,6 – центры симметрии плоскостей.

происходят только при переходе от одной ячейки к другой.

Согласно [3] тепловой поток dQ i , передаваемый излучением от элемента dS 1 горячей поверхности излучателя к элементу dS 2 холодной поверхности i-й ячейки лучеприемника ОРМ определяется соотношением:

dQ = 8,е₂ С ₀ [( 0 , 01 ^ ) ⁴ -( 0 , 01 T ₂ ) ⁴ ]cos(p_1;...x

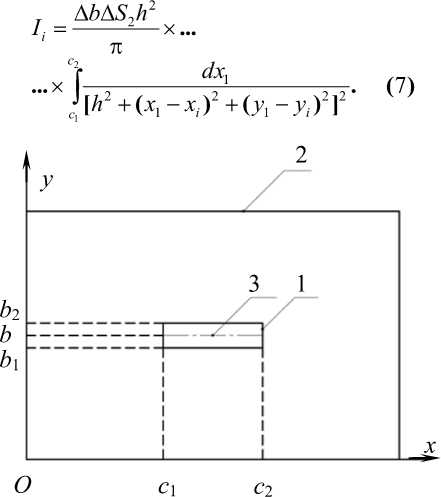
... х co$(p₂, • dS_xdS₂ 1 n r ², ( 1 ) где: Т – абсолютная температура; С 0 =5,67 Вт/(м² К⁴) –коэффициент излучения абсолютно чёрного тела; – степени черноты поверхностей излучателя и лучеприёмника; r i – линейное расстояние между элементами греющей поверхности dS 1 и нагреваемой поверхности i-й ячейки dS 2 ; φ 1 i , φ 2 i – углы меж-

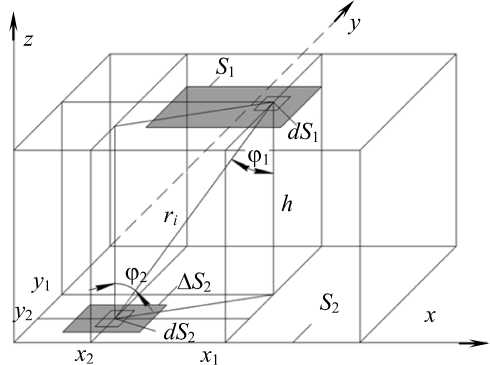
Рисунок 2. Расположение плоскостей излучателя S 1 и лучеприёмника S 2 в ортогональной системе координат

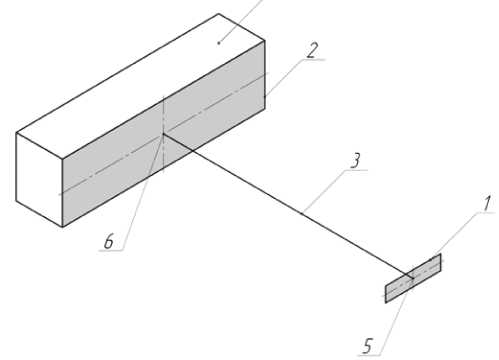
Процедура решения существенно упрощается, если площадь лучеприем-ника S2 разбить на достаточно большое количество одинаковых по размерам прямоугольных ячеек площадью ΔS2 с таким расчётом, чтобы выполнялось условие ΔS2<

Соотношение (1) упрощается, если учесть, что температуры Т1 и Т2 существенно различаются. Если первая соответствует температуре кварцевого излучателя нагревательного прибора (Т1≈900 К), то вторая близка к комнатной температуре (Т2≈300 К). Отсюда следует, что (Т1/ Т2)4 ≈ 102 и слагаемым (0,01 Т2)4 в уравнении (1) можно пренебречь. Таким образом dQ = 8,8,0, (0,01T, )4 со$ф„...х ... х со$(р2; • dSldS21 л^2,                       (2)

Для определения величины теплового потока Qi, попадающего от излучателя в i-ю ячейку площади лучепри-ёмника, уравнение (2) следует проинтегрировать дважды по S1 и ΔS2. dQ = 8,8₂С₀(0,01T,)⁴ j j cos(p,,...x

S1 S2

... x co$(p₂j • dS,dS₂ / nr²,                       (3)

Необходимо при этом иметь в виду, что плоскости S1 и S2 взаимно параллельны и следовательно cosф₁i = cosф₂i = h/ri, где h -дистанция обогрева.

Теоретические основы технологии дифференцированного обогрева производственных помещений. Математическая модель

Кроме того очевидно, что r²h² + (x1– x2i)² + (y1–y2i)². С учетом этого соотношения интеграл в уравнении (3) можно

представить в следующем виде:

h²

Ij = — X... л.

S1

S

dS

^[h² +(xi -x2i)²+ (У1 - y2i )²]²

>dS_x.  (4)

Принимая во внимание неизменность подынтегральной функции в пределах каждой ячейки плоскости S2 интегрирование уравнения (4) приводит к

результату:

S h²

Ii         ²

л

...

dS

S [ h² + (Xi- xi)²+(У1- y)²]².

Здесь с целью упрощения записи коор-

динаты центра ячейки переобозначены: x2i=xi ; y2i=yi.

Далее, определив   dS1=dx1dy1, представим интеграл (5) в виде:

S h²

^ = —2— x...

c₂

л b2

dy₁

c₁

b [ h² + (Xi-xi)² + (У1- y,.)² ]²

dx_x,  (6)

где с1, с2 и b1, b2 – координаты гра-

Рисунок 3. Нормальная ориентация плоскостей излучателя S 1 и лучеприём-ника S₂в в координатах xy:

1 –излучатель; 2 – лучеприёмник;3 –центр симметрии излучателя и лучеприёмника.

Параметр Δb определяется на основе принципа соответствия реального и модельного нагревателей и вычисляется по формуле [2]

bb = [ PKp Z(e Cl )](0,0171) -4,         (8)

где Кр – радиационный коэффициент, определяющий долю радиационного потока в теплоотдаче реального нагре-

ниц плоскости модельного излучателя S1 в системе координат x, y (см. рис.3).

Поскольку ширина плоского излучателя Δb=b2–b1 как правило существенно меньше его длины l=c2–c1, то изменением координаты y1 в пределах ширины излучателя можно пренебречь, приняв y1= b, где b= 0,5(b1+b2) – координата центра симметрии излучателя. Такое приближение позволяет вычислить внутренний интеграл в уравнении (6) и получить:

вателя.

Далее, переходя к обозначениям: h² +(b-y)²= a² и x₁ -xi =x ,     (9)

можно показать, что интеграл (7) является берущимся [4]. В результате искомое соотношение (3) представляется в алгебраической форме

Qi = eie2Ti"1C0(0,0171 )4h2bS2 bbHt,(10)

где:

H,=H,(x1 =c 2)-Hi.(x1 =C1),(11)

xx

H■ ( x ) =--5—^---¹----T" + ...

i¹    2 a² [ a² +(x-x₄ )²]

... -I--у arctg[(x, x).) Z a].(

2a³

Полученная система уравнений (8)–(12) позволяет решить задачу определения величины потока лучистой энергии Qi, попадающего от нагревателя в пределы i-й ячейки плоскости луче-приемника ОРМ.

Очевидно, что для решения этой задачи необходимо располагать совокупностью характеристик модельного нагревателя и ОРМ, входящих в качестве параметров в систему уравнений (8)– (12): Р, Кр, 81,82, Т1, с 1, с2, S2, AS2, b, Ab, l. Они в свою очередь определяются на основе базовой информации о характеристиках реального нагревателя и ОРМ [5], переработанной в соответствии с принципом адекватности реального и модельного объектов [2].

Вычисленные таким образом локальные тепловые потоки Qi образуют суммарный поток облучения, попадающий в створ лучеприёмника ОРМ in

Qоб     Qi ,                         (13)

i1

где n – количество ячеек в плоскости S2.

Вследствие пространственного рассеяния лучистой энергии поток Qоб составляет лишь часть первоначального потока модельного излучателя РКр. Доля его определяется коэффициентом облучения

Коб  Qоб/РКр.                     (14)

Далее, по причине имеющей место скважности поверхности лучепри-ёмника лишь часть потока облучения поглощается твёрдой фазой и обогревает, ОРМ. Поскольку долевая часть твёр- дой фазы на плоскости лучеприёмника зависит от величины её коэффициента скважности Кс [2], то величина греющего ОРМ лучевого потока определяется формулой:

Qг=Qоб (1-Кc) = РК_рК_об(1-К_с). ⁽¹⁵⁾

Следует иметь в виду, что величина Qг зависит от дистанции обогрева h, варьирование которой позволяет регулировать интенсивность обогрева ОРМ и тем самым изменять его температуру.