Теоретические подходы к расчету гидродинамического вибрационного фильтра

и режимные параметры в зависимости от характеристик очищаемой жидкости, присутствующих в ней загрязнение, а также требуемых эффективности и тонкости очистки и ресурса работы проектируемого устройств.

Для создания методики расчета и оптимизации режимных и конструктивных параметров ГДВФ необходимо создание теоретической модели процессов, имеющих место в нем, которая позволила бы выявить особенности механизмов сепарации и гидродинамики процессов, определить наиболее значимые с точки зрения влияния на конечный результат параметры, создать базу для разработки инженерной методики расчета.

К настоящему моменту законченной теоретической модели, описывающей сложную гидродинамическую картину течения двухфазной среды в предложенной авторами схеме гидродинамической вибрационной очистки нет. Есть отдельные теоретические модели, описывающие лишь некоторые отдельные механизмы, а не всю их совокупность.

В данной работе предложены теоретические подходы, используемые авторами при создании теоретической модели ГДВФ и на ее основе инженерных методик расчета и оптимизации его режимных и конструктивных параметров.

• 2.    ТЕОРЕТИЧЕСКИЕ ПОДХОДЫ К МОДЕЛИ ГДВФ

Теория гидродинамического вибрационного фильтрования базируется на частных случаях решения системы уравнений Навье-Стокса и неразрывности, записанных для несжимаемых ( р = const ) сред и нестационарных течений. Система уравнений имеет вид:

. в декартовых координатах :

р-

р-

р-

' д и + и * V д t	д и д и     д и । + у - - + w - — I =-д х д у     0 z у
' д у —— + и V д t	ду ду   д у ) —+ у —+ w — I = д х    д у     д ? у
' 0 w + и - .дt	0 w 0 w 0 w ) —+ у —+ w — I = д х д у 0 z у

д ² и д ² и д ² и I

_ д х ² д у ² O z ² J ’

(д 2 у д² у д 2 у )

⁺ Д ^- 1      ^{+ +} I

V дх ду

У д ² w д ² w д ² w ) ⁺4 д х? ТТ у ,

д и ду д а _

++= 0

V д х д у д z ’

где д - коэффициент динамической вязкости жидкости, Па - с , Д = р-V ;

р - плотность жидкости, кг/м³;

V - коэффициент кинематической вязкости жидкости (кинематическая вязкость), м²/с;

x , y , z – соответствующие проекции массовой силы на координатные оси.

. в цилиндрических координатах:

(ду    ду  у— ду у—    ду р-1    +у    +         -+у

| д t       д г   г   д—   г      д г

= K _д Р ₊ „ / ^д 2 Ч ₊ 1 .N _у ₊ 2 ^д 2 у. _ ² _- ^д Ч1 , ^д 2 Ч ^г д г I д г ² г д г г ² г ² д — ² г ² д— д г²

(ду   ду у ду у-у дуд р\^У +у - -^ +у -у I    W - у | =

| д     дг г д— г      д г у

-К 1 дР. Jд2у— J ду— — + 1 д2у—. 2 ду у =K—Т+Д-    +      2 + -+ ЧГ+ г д—   I дг   г дг  г  г2 д—  г д—  дг

ду ду у ду р- —z - + у z - +   -- ^z-

| д t       д г    г д—

у 2     д у

— + у---

r

^z д z

д p     ( д ² у

= K _ — + Д -1 ^у д z I д г ²

.         1 д ² у

+---- + —с---z г  дг   г2 д—2

1 ду

д2у )-+I д z2 )

ду у 1 д и   д w                   /ох

— + —+---+ — = 0           ⁽²⁾

\ д г   г г д—   д z    ’

где г, ф , z - соответственно радиальная, окружная и осевая координаты;

у , и , w и К_г , к _— , K_z - составляющие скорости и массовой силы в направлении этих координат.

Течение жидкости в ГДВФ можно разложить на 3 составляющие движения:

• 1)    продольное течение жидкости в канале между неподвижной ФП и корпусом фильтра при наличии равномерного отсасывания пограничного слоя – фильтрация через неподвижную перегородку;

• 2)    течение жидкости в условиях вращения ФП относительно неподвижного корпуса при наличии равномерного отсасывания пограничного слоя – фильтрация через вращающуюся перегородку;

2.1. Продольное течение жидкости между ФП и корпусом фильтра

3) течение жидкости в условиях вибрации (возвратно-поступательных движений) ФП при наличии равномерного отсасывания пограничного слоя – фильтрация через колеблющуюся перегородку.

Профиль скорости потока перепускаемой жидкости. Имеет место случай течения жидкости в кольцевой цилиндрической трубе с равно-

мерным отсасыванием пограничного слоя.

Система уравнений (1) имеет вид д w д у п

+= 0

д z     д у     ,

дw _  1 дp    д2w   д2w  у дw _  1 дp ду    р дz     ду2    ду2  V ду    Д дz .(4)

Граничными условиями при этом будут: w = 0 , у = у ₀ при у =0, w = 0 при у = h .

Общее решение уравнения (4) имеет вид

w ( у ) = _ ^V - expl у

у

-^- у

V

р - у

^А Р

■ — ^{- у +} C 2 .

Его решение при заданных граничных условиях

^w ( у ⁾ = —^ ^Р- ^- р - у ₀ A z

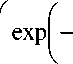
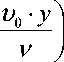
_ 1

у ₀

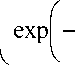
^у 0 ^- h V

_ 1

у

h

у

Q

2 - я - R-L ’

где Q – расход фильтруемой жидкости, м³/с;

R , L – соответственно радиус и длина ФП, м.

Удельные потери давления по длине ФП при течении жидкости в кольцевой трубе выражаются формулой

A p   , l р-^w ср.     8 ^- Д ^{- w} ср.

— = л ----=---—

A z     d 2 h ²

ср.

Q _. я\ D + h ) - h

где h – зазор между корпусом и ФП, м. Тогда формула (5) принимает вид:

^{w (} у ⁾ =

8 ■ V • w

ср.

exp

^у 0 'У

h • у

exp

у

V

- h

У

V

V

h

у

. (6)

Введем обозначения

у = У A = ^{/ h} w ( у )=^

h , v ,            wср.

Тогда формула (6) примет вид:

^{w (} у ^ A'

Г exp ⁽ - A_ у ^{) _} 1 _ _ ]

k exp ( - A ) - 1      J

Условие смыва частицы загрязнений, находящейся во взвешенном состоянии между ФП и корпусом, потоком перепускаемой жидкости. Для того, чтобы обеспечить оптимальные условия удаления частицы загрязнений из ГДВФ потоком перепускаемой жидкости, необходимо отбросить ее на минимальное расстояние у = h min , на котором величина скорости будет иметь максимальное значение.

Формула (7) позволяет определить величину скорости продольного потока в зависимости от рассто я ния y от ФП. Безразмерный коэффициент A в (7) есть ни что иное как показатель фильтруемости ГДВФ. Он служит для оценки влияния отсасывания пограничного слоя на распределение скорости в кольцевом зазоре между ФП и корпусом. A устанавливает взаимосвязь между такими параметрами гидродинамического фильтрования как коэффициент v кинематической вязкости жидкости, зазор h между ФП и корпусом и скорость V 0 фильтрации, что позволяет определить оптимальных конструктивные и режимные параметры ГДВФ для получения требуемой эффективности очистки.

На рис. 1 представлен в относительных координатах график зависимости скорости потока перепускаемой жидкости от расстояния между ФП и корпусом, выполненный при разных значениях показателя фильтруем о сти.

Как видно из рис. 1, при A =100 отсасывание пограничного слоя не влияет н а эпюру скорости продольного потока. При A =10 и менее вершина параболы смещается в сторону фильтровальной поверхности.

Величину h min можно определить из уравнения

aw(у )_   8 f A • exp(_ A • y)

A \ exp ( - A ) - 1 " 1

Тогда

1 . Г1 - exp ( - A y = - ■= • In I ------ i=y----

A ( A

TIL.

max

A ²

1+

k

A exp(- A)-1

^^^^^^^B

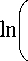
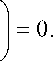
^{exp (} A ^{) _ 1} 1]

A ))

Уравнение (8) позволяет рассчитать минимальное расстояние h min от ФП, на которое нужно отбросить частицу загрязнений, чтобы обеспечить оптимальные условия ее смыва потоком перепускаемой жидкости. Уравнение (9) определяет величину скорости w max на этом расстоянии.

Траектория движения частицы жидкости. Траектория движения частицы жидкости может быть рассчитана из выражения

s(У) = J w(У) • dt = _J 8 У Wcp. h ^0n

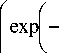
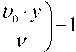
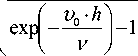
y h

• dt

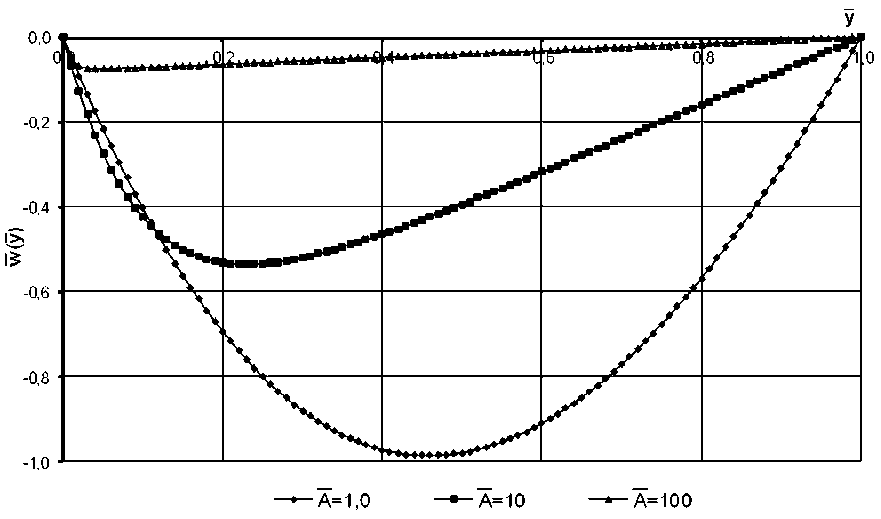
Рис. 1. Распределение продольных скоростей жидкости в кольцевом зазоре между ФП и корпусом

За время dt частица жидкости пройдет расстояние dy = v ° • dt . Тогда

^ ⁽ у ) = J wу ) • dy = "J 8- ^ ^J       u ₀     ^j h

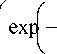
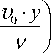
- 1

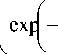
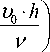
- 1

• 2.2. Окружное течение жидкости между ФП и корпусом

1) Течение жидкости, образованное вращением внутреннего цилиндра относительно неподвижного цилиндрического корпуса с рав- д2и v ди     д2и v ди

—+---= ° • —+---= °   (13)

д у ² v д у    ’ ду ² v д у

Граничными условиями являются следую щие выражения:

и = а • R , v = v° = const < ° при у = °, и = ° при у = h.

Общее решение уравнения имеет вид:

v _ Г v  L _ и = — •С1 • exp| — •у | + C2.

v V v  )

Его решение при заданных граничных условиях:

номерным отсасыванием пограничного слоя

Обозначения: пусть r₁ и r₂ – радиусы внутреннего и внешнего цилиндров, а Щ 1 - угловая скорость внутреннего цилиндра. Поскольку рассматриваемое течение можно считать плоским система (2) принимает следующий вид:

^{и (} у ⁾ = ^-

1 - exp	^L • (	h - у )
	L v

1 Г v₀ , 1 - exp| — hi

V v

• to-R.

и 2 Ap д2 и   д Г и ^ _ р—= л ;тт+^|-| = °.

r   A r д r² д r V r )

При этом граничными условиями будут сле дующие соотношения:

• и = r₁ • to ₁ при r = r₁ ;

• и = ° при r = r ₂ .

Решая уравнение (4) при заданных гранич ных условиях, получим

Введем обозначения:

у=у, A =

h

v° •h v

, ^{и (} у ⁾=

^{и (} у ⁾ to- R .

и =

2 2

r 2 ^- r l

r l ^ r 2

V

r

^{- r} 1

)

• r • ^ ;

)

-

-

д ² v  ( 1   v ) ди  1 и ²    v   1   д p

⁺11 чг⁺ 2 = ^_    ;(10)

д r   V r  v) д r  v r   r   д д r

д2 и Г1 v ^ д и и v и

- о.

2                                 2 ;

д r   V r v) д r r v r

dv v

— + - = ° .

dr r

Пусть v = v ° = const , тогда

1 и2 v = 1 дp v r r2 д д r ,

Тогда

^{и (} у ⁾ =

^{1 -} exp [ A -⁽£ - у ⁾ ] 1 - exp ( A )

Формула (15) позволяет определить величину окружной скорости в зависимости от расстояния y от ФП.

На рис. 2 представлен в относительных координатах график зависимости окружной скорости жидкости от расстояния между ФП и корпусом, выполненный при разных значениях показателя фильтруемости.

Как видно из рис. 2 при A =1,0 отсасывание

д ² и ( 1 v ^ д и и v и +1।.

д r2 V r v ) д r r2 v r

пограничного слоя практически не оказывает влияния на эпюру скоростей в кольцевом зазоре между ФП и корпусом, а скорости частицы жидкости повторяют характер кривой, описываемой уравнением (15), что соответствует случаю течения жидкости между вращающимся цилиндром с непроницаемы м и стенками и неподвижным корпусом. При A =100 отсасывание пограничного слоя вызывает резкое экспоненциальное снижение окружной скорости и на расстоянии у = °,1 от ФП эта скорость уже принимает нулевое значение, тем самым ухудшается способность фильтра к центробежной сепарации.

Решение возможно с применением численных методов.

2) Обтекание плоской пластины с учетом ограниченности пространства

Дифференциальное уравнение обтекания жидкостью плоской пластины имеет вид

• 2.3.    Течение жидкости при вибрации ФП

При отсутствии проницаемости ФП д2 w     д w 1 д w

+ v

ду2       ду v д t

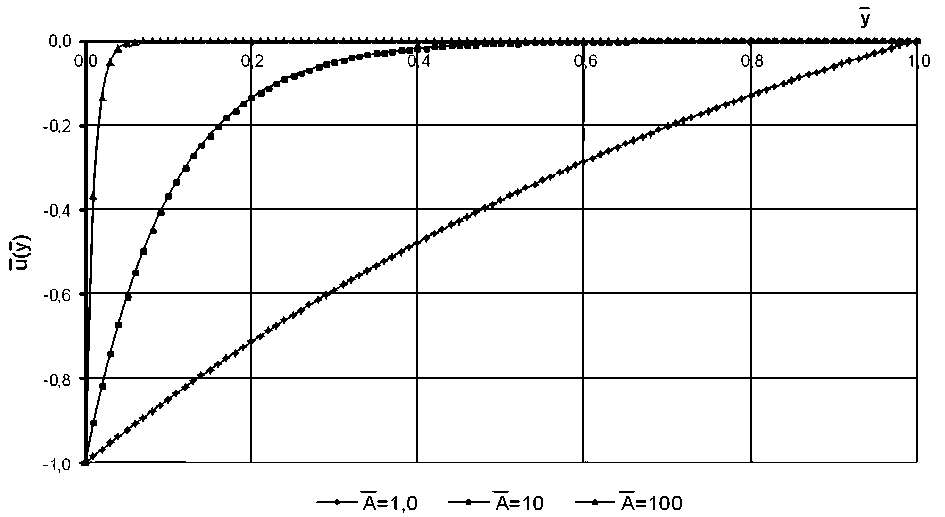
Рис. 2. Распределение окружных скоростей жидкости в кольцевом зазоре между ФП и корпусом

Граничные условия:

при y = 0 , w = A в • cos ( 2 • я • f в • t + a ) ;

при y = h, w = 0 , где Ав. – амплитуда вибрации, м;

f в. – частота вибрации, Гц;

a - сдвиг фазы колебаний, рад;

t – время, с.

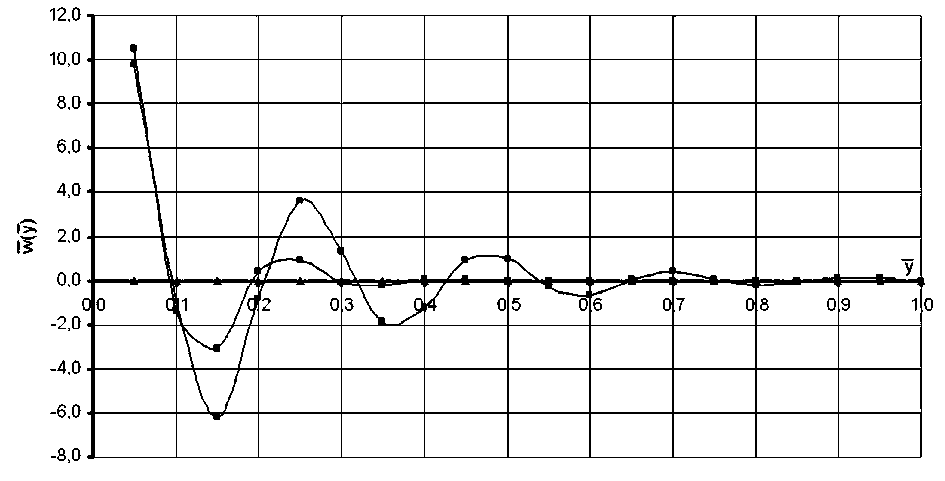
Уравнение может быть решено графическим методом. Решение уравнения представлено на рис. 3.

Рис. 3 также иллюстрирует влияние отсасывание пограничного слоя на эпюру скоростей при колебательном движении ФП: при A =100 пульсации жидкости практически не наблюдаются, в то время как при A =1,0 пульсации очевидны.

• 3.    ЗАКЛЮЧЕНИЕ

Предложенные подходы к теоретическому описанию гидродинамических процессов в ГДВФ позволяют создать его аналитическую динамическую и сепарационную модель. Адекватность предложенного теоретического подхода проверена путем сравнительных расчетов про-

_*_А=1.0 _ ^а=10 —^а=100

Рис. 3. Распределение продольных скоростей жидкости в кольцевом зазоре между ФП и корпусом филей скорости по некоторым полученным формулам и путем численных расчетов с использованием стандартной программы Ansys CFX.