Теоретический анализ взаимодействия рабочего органа при отделении отводков вегетативно размножаемых подвоев

Рис. 1. Схема взаимодействия срезанного побега с диском ножа

Направление падения срезанного побега зависит от его положения на диске и соотношения действующих на побег сил. Для определения последних применим принцип Даламбера, в соответствии с которым составим уравновешенную систему сил в векторной форме

Gn + N + F + F + P + P + P + P = 0,               (2)

П             х у r n кх ку где GП – сила тяжести побега, Н; N – нормальная реакция диска ножа на побег, Н; Fx и Fy – проекции силы сцепления соответственно на оси х и у, Н; Pτ и Pn – тангенциальная и центробежная силы инерции переносного движения, Н; Pкх и Pку – проекции силы Кориолиса соответственно на оси х и у, Н.

В связи с тем, что разница между радиусом r 0 исходного положения точки А побега на диске и радиусом диска R пренебрежимо мала, а траектория относительного движения комля по диску близка к окружности, считаем, что комлевая точка побега движется по окружности радиуса r с тангенциальным ускорением а τ =const, и кориолисову силу в расчет не принимаем.

С учетом принятых допущений векторное уравнение (2) в проекциях на координатные оси xyz подвижной системы с началом в точке А выглядит следующим образом:

P r - F x = 0;

P - F = 0;                                  (3)

_ N - Gn = 0.

Исходя из последнего равенства системы (3), имеем N=G П =mg , откуда

F=fmg .

Проекции силы сцепления F на осях х и у подвижной системы координат соответственно составят

F x =fmg∙ cos β ;     F y =fmg∙ sin β ,                                       (5)

где β – угол между осью х и направлением силы F .

Из второго уравнения системы (3) получим Pn=Fy или тоПr = fmg sin в. В начальный момент времени (t=0) шп=0, то есть топr = 0. При этих условиях fmg sin в = 0 только в том случае, если sin в = 0, то есть в=0о. В то же время из первого уравнения системы (3) видно, что Pt=Fx или maτ=fmg∙cosβ. Так как β=0о, то cos β=1 и следовательно aτ=fg.(6)

Величина угловой скорости точки А побега в переносном движении определяется выражением

ωП=ωПо+εt,(7)

где ω П о – начальная угловая скорость побега, рад; t – время отсчета, с; ε – угловое ускорение, с^-1

a

£ = —.(8)

r

Известно, что в относительном движении по диску ножа основание побега (точка А ) перемещается по траектории в виде логарифмической спирали [2], уравнение которой [3]

R=r e ^aθ ,

где r и θ – текущие полярные координаты; a =ctgα=const; α – угол между касательной к спирали и радиусом r , близкий к прямому [2]; е – основание натурального логарифма.

Таким образом, с момента касания до момента схода побега с диска в относительном движении основание побега переместится по диску на угол n ln( R / Г0 ) O =------

a где R – радиус диска ножа, м; r0 – радиус точки исходного касания торца побега после среза, м.

При равнопеременном движении путь, пройденный телом за время t, составляет

a t2

S = S0 + Л01 +—|—, где Sо - начальная точка отсчета, м; Л - начальная скорость, м/с. С учетом начальных условий (Sо=О, Ло=0), принятых ранее допущений (rо®R=r) и равенства (6) получим: вначале S = Or = (a .12.) / 2, а затем

tex = 42Or/fg ,

где t сх – время с момента касания побегом диска ножа до его схода, с.

За это же время диск перенесет побег в направлении своего вращения на угол ф = ф ₀ + О 0 1 + £ t ² /2 , где ф о - начальная точка отсчета, рад; ш о - начальная угловая скорость, с^-1; ε – угловое ускорение, с^-2 ( ε=а τ /r=fg/r ). С учетом начальных условий ( φ 0 =0, ω 0 =0) и равенства (8) имеем

ф=Q=HR/r) a

где φ – угол схода побега с диска, рад.

= a , t_a = 4 ^{2 f}g^Q

, а угловая составляет

При этом линейная скорость схода Р сх

v. = 42 fgQ / r.

Дифференциальные уравнения вращения срезанного побега относительно осей х и у имеют вид

Jx= SMx(Pi); Jy= ZMy(Pi),         (14)dt                    dt

Ю р х и Ю р _y - угловые скорости

где J x и J y – моменты инерции ствола относительно осей х и у , Н∙м²;

^ M x (P i ) и ^ M_y ( P i ) - алгебра-

вращения побега относительно осей х и у соответственно, с^-1;

ические суммы моментов всех действующих на побег сил относительно осей х и у , Н∙м.

Ориентируясь на данные таблицы и рисунка 2, полученные на основе измерений, проведенных в 2010 году научным сотрудником ВНИИС им. И.В. Мичурина, кандидатом сельскохозяйственных наук Е.А. Капли-ным, считаем

т т   3 ml2

J = J =--- C

,

x ^y 2

где l C =l/ 3 – расстояние от осей поворота до центра тяжести побега, м; l – длина побега, м; m – масса побега, кг.

Параметры отводков клоновых подвоев 62-396 и 54-118

Параметр	Вариационные показатели
	М , см	σ , см	m , см	Р , %	V , %
Подвой 62-396
Высота побега l	61,49	17,72	1,87	3,04	28,82
Высота центра тяжести l C	16,88	5,39	0,57	3,37	31,94
Отношение l C /l	0,276	0,04	0,005	1,73	16,2
Подвой 54-118
Высота побега l	80,64	27,66	2,92	3,62	34,29
Высота центра тяжести l C	27,17	8,08	0,85	3,13	29,73
Отношение l C /l	0,345	0,047	0,005	1,43	13,6

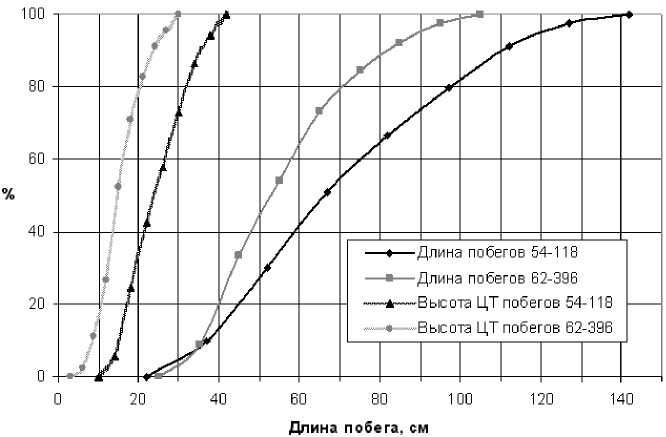
Рис. 2. Интегральные кривые распределения длины побегов и расстояния до центра тяжести

Принимая во внимание (15) и обозначения рисунка 1, имеем: относительно оси х

	3 ml 2 d a epx ----p— — PL, cos y + GL sin Y ■             (16) n C          x          C          x ;                         ( ) 2 dt
относительно оси у	3ml 2 da m    вр^ — PL cos y + GL sin y          (17) 2      dt         n C       y       C       y .                 (17)

Так как G п =mg, P n — m a _nГ и P_Т=mfg, после замены в (16) и (17) и некоторых преобразований получим:

da

вр х

dt

da

вр y

dt

• —    2г (®П r cos Yx + g sin Yx), 3lC

• —    2- g(fcos Yy + sin Yy).3lC

Перед интегрированием (18) и (19) умножим почленно их левые и правые части на dγ и, учитывая, что dγ∙dω вр / dt=ω вр ∙dω вр , получим:

^а врх                     2 Y x /

[a da  ——f(a2rcosy + gsinY )dY врх     врх                 П           x               x x ,

0                 3l 0

C ⁰

^a epy

[ a da

вр y вр y

Q ^Yy /

— Tg J(f cos Yy + sin Yy ^Yy.3lC 0

Интегрирование (20) и (21) с учетом того, что 1= 3lc (или lC = 31), приводит к следующим уравнени- ям:

а вр х

4 [фП г sin Yx + g (1-

,

а вр y

.

Геометрическое сложение векторов О врх и Ф вр у дает вектор О вр абсолютной угловой скорости вращения побега относительно его мгновенной оси вращения

а = Оврх + авру.

При этом плоскость вращения побега расположена перпендикулярно его мгновенной оси вращения и отклонена от оси х на угол

^ = arctg

а

вр х

а

вр у

,

где μ – угол плоскости падения побега в относительном движении, рад.

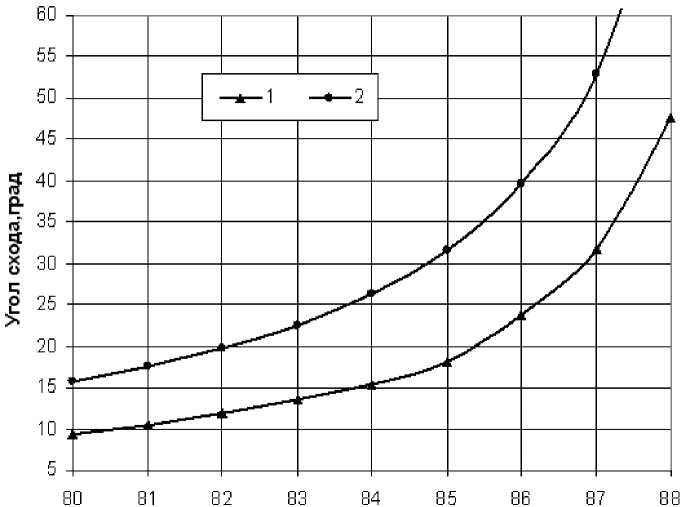
Фактически, с учетом угла схода φ побега с диска, вычисленного по уравнению (12) (рис. 3), сектор падения срезанного побега смещен в сторону вращения дискового ножа.

Постоянная траектории, град

Рис. 3. Расчетный угол схода побегов с диска ножа при R/r 0 , равном: 1 – 1,05; 2 – 1,03

Выводы. Таким образом, теоретический анализ взаимодействия срезанного побега с дисковым ножом показывает, что единичный побег неизбежно упадет в направлении движения машины. Только побеги, срезанные одной наружной боковой кромкой ножа, расположенной по касательной к линии ряда единичных побегов с линейной скоростью режущей кромки, направленной против хода машины, могут избежать повторных воздействий ножа и травмирования. В иных случаях необходимы дополнительные устройства, обеспечивающие отвод побегов после их отделения от маточного растения.