Теоретический расчет давления в емкостях, заполненных дискретной средой

Ведение. В теории взаимодействия сыпучих материалов со стенками емкости важное место отводится определению величины давления материала на стенки емкости. Известно, сыпучий материал обладает и свойствами жидкости, и свойствами твердого тела. Модель идеального сыпучего материала предполагает наличие силы сухого трения в местах контакта частиц между собой и стенками емкости. От величины давления в горизонтальном и вертикальном направлениях зависит выбор емкости для хранения. Интересным представляется вопрос определения параметров, отвечающих за величину давления.

Теоретический расчет давления в емкостях. В сыпучем материале вертикальное P z и горизонтальное Р y давление связаны соотношением:

P y = k • P z ,

где k – так называемый боковой коэффициент. Это соотношение используется, в частности, и для расчета давления на стены элеваторов. Однако, несмотря на то, что соотношение (1) известно давно [1], аналитического выражения для этого коэффициента до сих пор не получено.

В данной работе делается попытка на основании аналитического исследования давления сыпучего материала в щелевом бункере получить в общем виде выражение для бокового коэффициента k.

Рассмотрим бесконечно длинную, вдоль оси ОХ, емкость с сужающимися книзу стенами, т.е. щелевой бункер, с углом наклона стенки к         z yY вертикали α (рис. 1).

Система уравнений для определения дав-

HW ления в сыпучем материале имеет вид [2]:

Y- g = ^{( 1} + ц 2 ) ^^d P^L, о z

, dPz _    dPz к--= Ц i--, dy       dz

объем

Z

Рис. 1. Щелевой бункер и оси координат

Py = к • Pz, где цi - коэффициент внутреннего трения; у - объемная плотность сыпучего материала.

Проинтегрируем первое уравнение в системе (2) по координате у: от -W d до +W d (см. рис. 1), т.е. перейдем от элементарного объема к элементарному горизонтальному слою толщиной dz:

Y • g • dz • 2 • W d = ( 1 + ц^ У-P^ • dz • 2 • W d + C . о z

Константа интегрирования С по физическому смыслу будет представлять собой вертикальную компоненту силы, действующей на боковые поверхности элементарного слоя. Рассмотрим контакт элементарного, горизонтального слоя с боковой поверхностью щелевого бункера (рис. 2). Как видно из рис. 2, к основному элементарному слою ABCD необходимо еще добавить два (по одному на каждую сторону бункера) треугольных слоя – BEC . Если вместо сыпучего материала в бункере находилась бы идеальная жидкость, то вертикальная компонента силы реакции стенки бункера в точности уравновесила силу тяжести этих элементарных треугольных слоев. В первом приближении распространим этот вывод и на случай сыпучего материала.

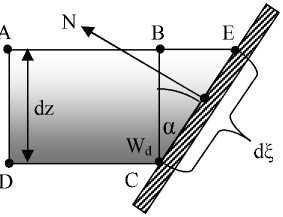
Рис. 2. Контакт элементарного слоя с боковой поверхностью бункера

Следовательно, из сил, действующих на боковые стороны элементарного слоя, осталась лишь вертикальная компонента силы трения. Силу трения определим как силу сухого трения FTP = μe N, где μе – коэффициент внешнего трения. Очевидно, что сила реакция стенки N будет определяться давлением, действующим на боковую стенку. В этом случае константа интегрирования С имеет следующее выражение:

dz

C = 2 ■ ц_е ■ N ■ cos a = 2 ■ ц_е ■ P ■ d^ ■ cos a = 2 ■ ц_е ■ P ---cos a .

cos α

Далее, обобщим соотношение (1):

P(в) = Pz-[1 -(1 -k)• sin в], где Р – давление в сыпучей среде по некоторому произвольному направлению; β – угол между этим направлением и осью OZ.

Множитель перед квадратной скобкой – вертикальное давление. Это естественно, так как мы рассматриваем движение сыпучего материала под действием сил гравитации. Следовательно, вертикальное давление будет основным, ведущим фактором, под действием которого формируется все поле давления в сыпучем материале. В этом случае, если направление совпадает с осью OZ, то угол β = 0 и P(0) = Pz = Pz. Если направление совпадает с осью OY, то угол β = π/2 и P(π/2) = Py = k Pz . Очевидно, что этот коэффициент должен зависеть от свойств са- мого сыпучего материала.

Подставив в (4) выражение (5), получим:

C = 2 ■ ц_е ■ P ■ dz = 2 ■ ц_е ■ dz ■ P_z ■ [ 1 - ( 1 - k ) ■ cos a ] .

N и

Здесь использовано то обстоятельство, что угол между направлением силы реакции осью OZ равен π/2 – α . С учетом (6) уравнение (3) преобразуется следующим образом:

• Y ■ g ■ dz ■ 2 ■ W_d = ( 1 + ц 2 L^ z ■ dz ■ 2 ■ W_d + 2 ■ ц ■ dz ■ P_z ■ [ l - ( 1 - k ) ■ cos a ] .

d                5 z              d         e ^z

Приведем это уравнение к стандартному виду:

^d P z + Ц е • P z •[ ! ^{-( 1} - ^k ) ■ ^{cos a ]} - Y ■ g = 0 5 ^{z    ( 1} + Ц² y(W - ^z ■ tga )     ¹ + ц²

Здесь использовано соотношение:

W d = W - z ■ tga .

Решение уравнения (7) имеет вид: ^A

P = c ■(- w + b■ z) b---(- W + b■ z), z v           ’ A - b v           ’ где для сокращения записи введены следующие обозначения:

■ cos a ]

b = tga  B = ^{Y g} ₂  A =

1 + Ц-

^{1 + ц}

На поверхности бункера давление должно равняться нулю. Из этого условия получим выражение для константы интегрирования:

C = —— • ( - W ) ^1- A .

A - b ^{v 7}

При этом уравнение (9) преобразуем к виду:

P z =

B - ( W - b • z

A - 1

A - b

.

Из выражения (10) следует, что при ц е ^ о , А ^ о . При этом P_z ^ ^Y g z , что со- 1 + ц;

ответствует физическому смыслу исследуемой задачи.

Рассмотрим теперь предел выражения (11) при стремлении стенки щелевого бункера к вертикали ( α → 0, b → 0 ):

lim P„ = lim b ^ о ^z b ^ о

B - ( W - b • z

A

A - b

B • W

•

A

1 - lim b ^ о

V

A

W - b • z I b

W J

.

Таким образом, мы имеем дело с неопределенностью типа 1 ” . Для ее раскрытия найдем сначала предел логарифма этой неопределенности:

lim b ^ о

A

, IW - b • z | b lnl---------------I

V   w 7

г A 1 I и z = lim — ln I 1 - b —

b ^ о b

W

.

I z I

Для этого разложим логарифм в ряд по степеням I b • — I :

г A 1 h A z lim — ln I 1 - b —

b ^ 0 b

W

= lim b ^ о

A b

\

—

V

b - — - W

—

.

.

.

—

A • —.

W

Отсюда вытекает, что:

lim b ^ о

A

W - b • z | b w 7

I             z I

= exp - A — .

V     w J

Следовательно, вертикальное давление (при b → 0 ) будет стремиться к пределу:

_n B-W 1

lim P7 =--1 - exp b ^ о z A         p

—

A • —

W

.

Подставляя в это выражение значения В и А , получаем:

lim P = b ^ о ^z

Y • g • W

Ц е • к

• 1 - exp

-

^Ц е • ^{k z}

•

_V 1 + Ц W ₇

.

Данное выражение совпадает с хорошо известным решением для прямоугольного силоса [3]. При выводе последнего уравнения учтено, что lim A = b ^ о

Ц е • к

1 + Ц-

. Таким образом, дока-

зана преемственность решений для прямоугольного силоса и щелевого бункера.

Введем теперь в решение (11) зависимость от координаты у . Аналогично [2] эту зависимость представим в виде:

BW - b • [ z ^{- (} W - y ) • tgX ] L ( ^W - b • [ z ^{- ( w} - y ) • tgx l ) A - 1 1 - I                                               I

A - b             I         W         )

где x - угол естественного откоса.

Потребуем теперь, чтобы решение (12) удовлетворяло второму уравнению системы (2). Найдя первые производные от (12) по у и z, и подставив их в (1), получаем:

k _ M i _ tg^

.

tgχ  tgχ

Таким образом, получено аналитическое выражение бокового коэффициента для сыпуче-

го материала, находящегося

в

пространства щелевого бункера на области

щелевом бункере. Уравнение (13) совпадает с выражением, полученным в [2] для сыпучего материала, находящегося в насыпи. Тем самым подтверждается предположение о том, что боковой коэффициент зависит от свойств самого сыпучего материала и не зависит от вида емкости, в которой он находится.

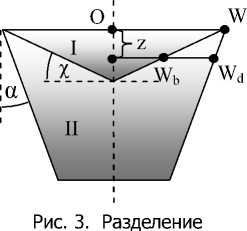
Однако решение в форме (12) не удовлетворяет нулевому граничному условию на поверхности бункера. Для выполнения этого условия, все пространство щелевого бункера разобьем на две области (рис. 3).

Решение в области I представим в виде [2]:

Решение в области

II

p i ₌ Y ^- g ^P z

1 + ^i будем искать в виде:

- z .

P z^II

_ B - { W - b - [ z - ( W - y ) - tg x D

A - b

1 - ( ^{W - b -[ z - ( w -} y ^)- tg x ] I A ^{- 1}

W

+ Jlg . W - y ) - tg x . (15)

¹ + Ц 2

На линии z = 0, y = W решение (15) обращается в нуль. На границе областей, определяемой уравнением y _ W_b; z _ ( W - W_b ) - tgx (см. рис. 3), первое слагаемое решения (15) обращается в нуль, а второе слагаемое переходит в P z ^I . Таким образом, выполнено граничное условие на поверхности бункера. При μ е → 0 решение (14) преобразуем к виду:

P I ^_ V" g 2^ ^{- [} z ^-( W ^- у ^)- tgX ] + Tg 2^ ^{-( W -} у ^)- tgX ,

1 + M i                       ¹ + M i

Yg или, преобразовав, получим: P _ ——- z, что соответствует физическому смыслу задачи.

• 1    + M i

Итак, мы видим, что решения (14) и (15) удовлетворяют граничным условиям и предельному переходу к идеальной жидкости.

График зависимости давления, рассчитанного по формулам (14), (15), от координаты z , при α = 30⁰, у = 0 и y = W = 3,5 м , представлен на рис. 4. Как видно из рисунка, давление с ростом z растет, достигает экстремума, а затем падает до некоторого минимума. Относительное положение максимума давления зависит от параметров бункера.

Таким образом, для идеального сыпучего материала в щелевом бункере найдено вертикальное давление (15). Горизонтальное давление определяем с использованием третьего уравнения системы (2), выражений (13) и (15).

Кроме того, исходя из экспериментально измеряемых параметров сыпучего материала, получено выражение (13) для коэффициента k, связывающего вертикальное и горизонтальное давление, так называемого бокового коэффициента [1]. Этот коэффициент определяется только параметрами самого сыпучего материала (углом внутреннего трения ψ и углом естественного откоса χ). В предельном случае, при стремлении к нулю коэффициента внутреннего трения (идеальная жидкость), этот коэффициент стремится к единице, так как в этом случае к нулю будет стремиться и угол естественного откоса. При этом идеальный сыпучий материал переходит в идеальную жидкость.

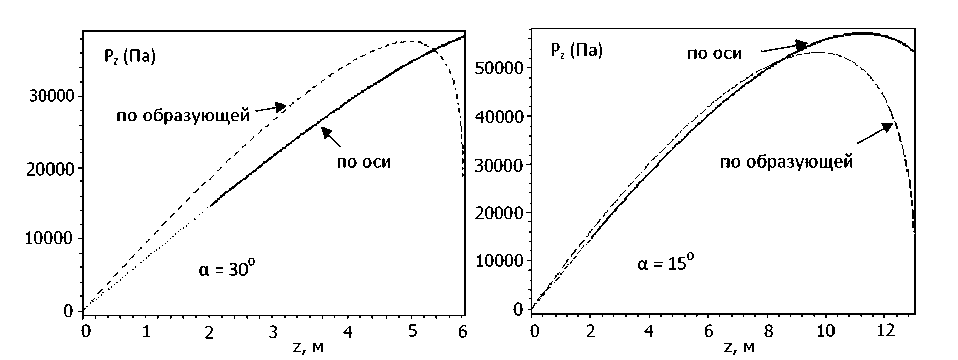
Рис. 4. Вертикальное давление в щелевом бункере вдоль осевой и образующей боковую поверхность линий при различных углах наклона стенки бункера α: γ = 800 кг / м3; ψ = 160; φ = 200; χ = 300; W = 3,5 м

До настоящего времени для определения численного значения бокового коэффициента используют эмпирические или полуэмпирические соотношения. Так, например, при инженерных расчетах для вычисления этого коэффициента используют следующую эмпирическую формулу:

k = V—,                               (16)

• 1    - v

где ν – коэффициент поперечной деформации. Однако само измерение этого коэффициента для сыпучих материалов вызывает большие трудности. К тому же по этой зависимости трудно установить предел, к которому стремится боковой коэффициент при переходе от сыпучего материала к идеальной жидкости.

В работе [4] приводятся опытные значения коэффициента бокового давления, в частности, для пшеницы k = 0,3 – 0,6 , что соответствует приведенным выше расчетам по формуле (13).

На практике для расчета давления на стены элеваторов используют следующую эмпирическую формулу для бокового коэффициента:

k = tg ² f 45 0 - ^ ) .                                  (17)

Это более реальное выражение для бокового коэффициента. Из этого выражения, в частности, следует, что при переходе к идеальной жидкости (при ψ → 0 ) боковой коэффициент стремится к единице в соответствие с законом Паскаля. Для зерна рекомендуется принимать коэффициент k = 0,44 . Однако в этом случае из (17) вытекает, что угол внутреннего трения должен быть равным ψ = 23⁰ , что расходится с экспериментальными данными. Выражение (17) нельзя считать универсальным из-за отсутствия в нем важнейшей характеристики сыпучего материала – угла естественного откоса. В [3] приводится следующее выражение для бокового коэффициента:

k =     ^{tg 2 e}     ,

• 2    + tg^ - tge

где β – угол укладки частиц сыпучего материала. Эта формула получена на основании представлений о дискретной модели сыпучего материала. При этом сыпучий материал моделируется абсолютно упругими шарами одинакового диаметра, имеющими правильную геометрическую упа- 167

ковку. Для пирамидальной укладки зерновой пшеницы угол укладки равен β = 43⁰ . В (18) угол φ – угол внешнего трения. Таким образом, в выражение для бокового коэффициента не входят обычно измеряемые параметры самого сыпучего материала: угол внутреннего трения, угол естественного откоса. Свойства самого сыпучего материала здесь представлены только теоретически введенным углом β , который экспериментально не измеряется. Поэтому по (18) невозможно определить предельное значение бокового коэффициента при переходе идеального сыпучего тела в идеальную жидкость. При φ = 20⁰ коэффициент k, рассчитанный по (18), получается равным k = 0,37 , что несколько меньше, используемого на практике значения.

Выводы. Таким образом, можно считать, что расчеты бокового коэффициента дают хорошее согласие с экспериментом. Формула (13) отражает физический смысл исследуемого параметра, удовлетворяет условиям перехода сыпучего материала к идеальной жидкости.